4.1.3认识三角形(第三课时)中线课件 (20张PPT) - 2024--2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.1.3认识三角形(第三课时)中线课件 (20张PPT) - 2024--2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 18:17:35 | ||
图片预览




文档简介
(共20张PPT)
4.1.3 认识三角形(第三课时)
成都市泡桐树中学
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
用铅笔可以支起一张均匀的三角形卡片,你能找到这个支撑点吗?
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
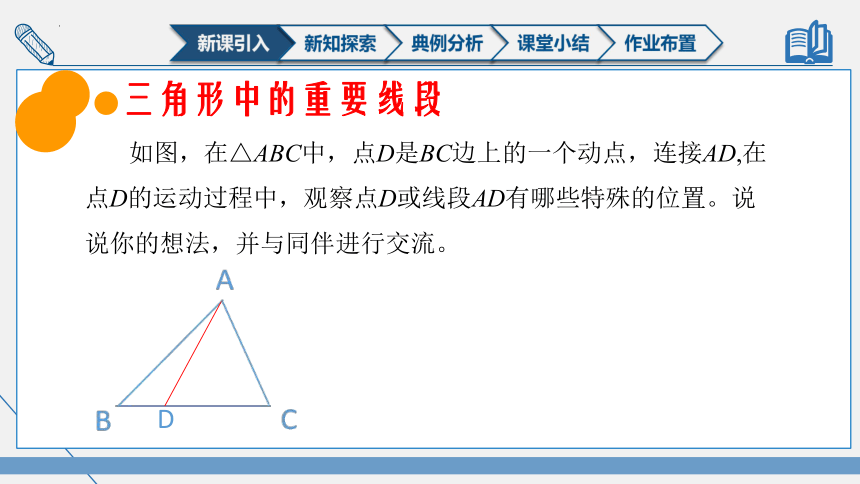
如图,在△ABC中,点D是BC边上的一个动点,连接AD,在点D的运动过程中,观察点D或线段AD有哪些特殊的位置。说说你的想法,并与同伴进行交流。
D
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
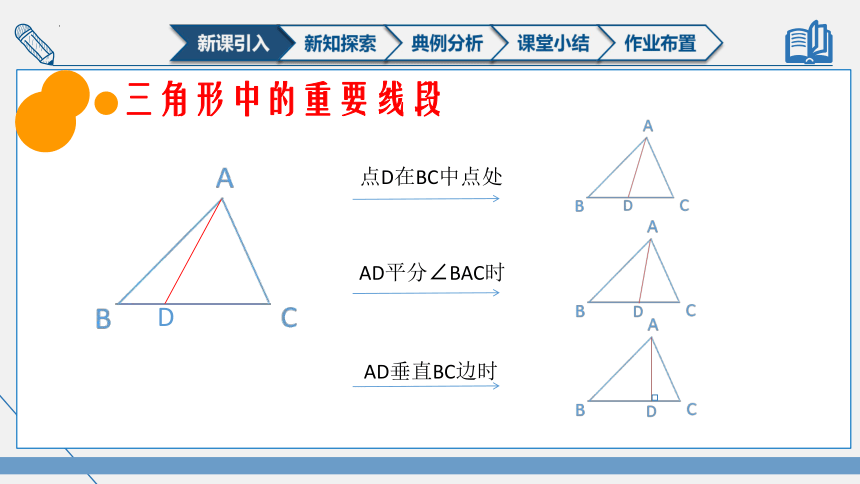
D
点D在BC中点处
AD平分∠BAC时
AD垂直BC边时
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线
几何语言:∵AD为BC边上的中线
∴BD=DC= BC
反之: ∵D是BC边的中点(BD=DC= BC)
∴线段AD为BC边上的中线
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
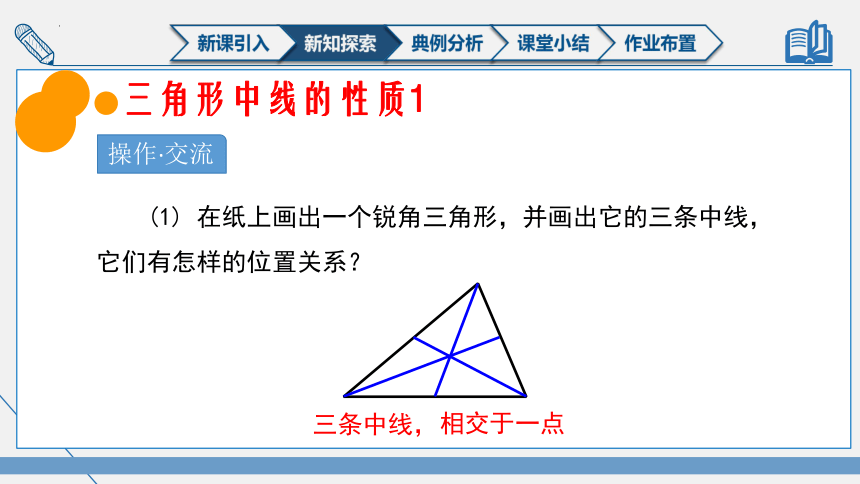
(1) 在纸上画出一个锐角三角形,并画出它的三条中线,它们有怎样的位置关系?
操作·交流
三条中线,
相交于一点
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
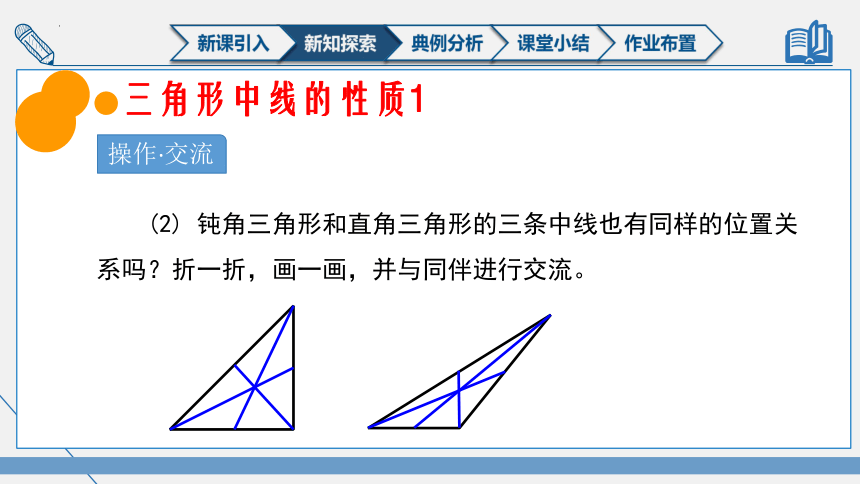
(2) 钝角三角形和直角三角形的三条中线也有同样的位置关系吗?折一折,画一画,并与同伴进行交流。
操作·交流
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
三角形的三条中线交于一点,这个点称为三角形的重心.
归纳总结:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)如图,已知AD,BE,CF是△ABC的三条中线.
①AC=2AE= 2EC ;
CD= BD ;AF= AB;
2EC
BD
典例分析
新课引入
新知探索
课堂小结
作业布置
变式:如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.
三角形的两条中线交于一个点,连接交点和顶点的线段必平分第三边。
.
推论:
三角形的中线的应用
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
1. 如图,已知BD是△ABC的中线,AB=8,BC=6,则△ABD和△BCD周长的差是( A )
A. 2 B. 4
C. 3 D. 5
A
三角形一边上的中线分出的两个三角形的周长差=另两边之差
归纳总结:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)在△ABC中,已知AC=2BC,边BC上的中线AD把△ABC的周长分成60和40的两部分,求边AC和AB的长.
解:∵AD是BC边上的中线,∴BD=CD.
设BD=CD=x,则BC=2x.
又∵AC=2BC,∴AC=4x.
分下列两种情况:
①若AC+CD=60,AB+BD=40,
则4x+x=60,x+AB=40,
解得x=12,AB=28.
则AC=4x=48,AB=28,BC=2x=24.
因为28+24>48,所以符合三角形三边关系.
②若AC+CD=40,AB+BD=60,
则4x+x=40,x+AB=60,解得x=8,AB=52.
则AC=4x=32,AB=52,BC=2x=16.
因为32+16<52,所以不符合三角形三边关系.
综上所述,AC=48,AB=28.
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质2
(3) 如图,在△ABC 中,AD 是△ABC 的中线.试判断
△ABD 和△ACD 的面积有什么关系?为什么?
操作·交流
B
C
D
A
答:相等.
h
∵AD为△ABC中BC边上的中线
∴BD=DC
∴S△ABD=S△ACD
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质2
三角形的中线分三角形为面积相等的两个三角形
.
归纳总结:
B
C
D
A
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
我们知道,三角形一边上的中线将这个三角形分成两个面积相等的三角形.如图1,AD是△ABC边BC上的中线,则S△ABD=S△ACD.
(1)如图2,已知△ABC的中线AD,BE相交于点F,△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
解:(1)S△ABF=S四边形CEFD. 理由如下:
因为AD和BE是△ABC的两条中线,
所以S△ABD=S△ACD=S△BCE=S△ABE= S△ABC.
因为S△ABD=S△ABF+S△BDF,SBCE=S△BDF+S四边形CEFD,
所以S△ABF+S△BDF=S△BDF+S四边形CEFD. 所以S△ABF=S四边形CEFD.
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)如图3,在△ABC中,已知点D,E,F分别是线段BC,AD,CE的中点,且S△ABC=8,求△BEF的面积.
解:(2)因为点D,E分别为BC,AD的中点,
所以S△ABD=S△ACD= S△ABC=4,
S△BDE= S△ABD=2,S△CDE= S△ACD=2.
所以S△BCE=S△BDE+S△CDE=4.
因为点F是CE的中点,所以S△BEF= S△BCE=2.
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
1. 如图,在△ABC中,E是中线AD的中点.若△AEC的面积是1,则△ABD的面积是 2 .
(第1题图)
2
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
变式:如图,在△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,求△ABC的面积。
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质3
(3) 用铅笔可以支起一张质地均匀的三角形卡片,怎样确定这个点的位置?
操作·交流
重心
重心是三角形的三条中线的交点,位于中线靠近底边的三等分点处
归纳总结:
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
1、三角形的三条中线交于一点,这点叫做三角形的重心(中线的三等分点)
2、三角形一边上的中线分出的两个三角形的周长差=另两边之差
3、三角形的中线把三角形分成两个面积相等的三角形。
4.1.3 认识三角形(第三课时)
成都市泡桐树中学
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
用铅笔可以支起一张均匀的三角形卡片,你能找到这个支撑点吗?
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
如图,在△ABC中,点D是BC边上的一个动点,连接AD,在点D的运动过程中,观察点D或线段AD有哪些特殊的位置。说说你的想法,并与同伴进行交流。
D
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形中的重要线段
D
点D在BC中点处
AD平分∠BAC时
AD垂直BC边时
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线
几何语言:∵AD为BC边上的中线
∴BD=DC= BC
反之: ∵D是BC边的中点(BD=DC= BC)
∴线段AD为BC边上的中线
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
(1) 在纸上画出一个锐角三角形,并画出它的三条中线,它们有怎样的位置关系?
操作·交流
三条中线,
相交于一点
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
(2) 钝角三角形和直角三角形的三条中线也有同样的位置关系吗?折一折,画一画,并与同伴进行交流。
操作·交流
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质1
三角形的三条中线交于一点,这个点称为三角形的重心.
归纳总结:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)如图,已知AD,BE,CF是△ABC的三条中线.
①AC=2AE= 2EC ;
CD= BD ;AF= AB;
2EC
BD
典例分析
新课引入
新知探索
课堂小结
作业布置
变式:如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.
三角形的两条中线交于一个点,连接交点和顶点的线段必平分第三边。
.
推论:
三角形的中线的应用
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
1. 如图,已知BD是△ABC的中线,AB=8,BC=6,则△ABD和△BCD周长的差是( A )
A. 2 B. 4
C. 3 D. 5
A
三角形一边上的中线分出的两个三角形的周长差=另两边之差
归纳总结:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)在△ABC中,已知AC=2BC,边BC上的中线AD把△ABC的周长分成60和40的两部分,求边AC和AB的长.
解:∵AD是BC边上的中线,∴BD=CD.
设BD=CD=x,则BC=2x.
又∵AC=2BC,∴AC=4x.
分下列两种情况:
①若AC+CD=60,AB+BD=40,
则4x+x=60,x+AB=40,
解得x=12,AB=28.
则AC=4x=48,AB=28,BC=2x=24.
因为28+24>48,所以符合三角形三边关系.
②若AC+CD=40,AB+BD=60,
则4x+x=40,x+AB=60,解得x=8,AB=52.
则AC=4x=32,AB=52,BC=2x=16.
因为32+16<52,所以不符合三角形三边关系.
综上所述,AC=48,AB=28.
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质2
(3) 如图,在△ABC 中,AD 是△ABC 的中线.试判断
△ABD 和△ACD 的面积有什么关系?为什么?
操作·交流
B
C
D
A
答:相等.
h
∵AD为△ABC中BC边上的中线
∴BD=DC
∴S△ABD=S△ACD
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质2
三角形的中线分三角形为面积相等的两个三角形
.
归纳总结:
B
C
D
A
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
我们知道,三角形一边上的中线将这个三角形分成两个面积相等的三角形.如图1,AD是△ABC边BC上的中线,则S△ABD=S△ACD.
(1)如图2,已知△ABC的中线AD,BE相交于点F,△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
解:(1)S△ABF=S四边形CEFD. 理由如下:
因为AD和BE是△ABC的两条中线,
所以S△ABD=S△ACD=S△BCE=S△ABE= S△ABC.
因为S△ABD=S△ABF+S△BDF,SBCE=S△BDF+S四边形CEFD,
所以S△ABF+S△BDF=S△BDF+S四边形CEFD. 所以S△ABF=S四边形CEFD.
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
(2)如图3,在△ABC中,已知点D,E,F分别是线段BC,AD,CE的中点,且S△ABC=8,求△BEF的面积.
解:(2)因为点D,E分别为BC,AD的中点,
所以S△ABD=S△ACD= S△ABC=4,
S△BDE= S△ABD=2,S△CDE= S△ACD=2.
所以S△BCE=S△BDE+S△CDE=4.
因为点F是CE的中点,所以S△BEF= S△BCE=2.
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
1. 如图,在△ABC中,E是中线AD的中点.若△AEC的面积是1,则△ABD的面积是 2 .
(第1题图)
2
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的中线的应用
变式:如图,在△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,求△ABC的面积。
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形中线的性质3
(3) 用铅笔可以支起一张质地均匀的三角形卡片,怎样确定这个点的位置?
操作·交流
重心
重心是三角形的三条中线的交点,位于中线靠近底边的三等分点处
归纳总结:
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
1、三角形的三条中线交于一点,这点叫做三角形的重心(中线的三等分点)
2、三角形一边上的中线分出的两个三角形的周长差=另两边之差
3、三角形的中线把三角形分成两个面积相等的三角形。
同课章节目录
