4.3.4 全等的判定 课件(共13张PPT)2024--2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.3.4 全等的判定 课件(共13张PPT)2024--2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 18:25:15 | ||
图片预览




文档简介
(共13张PPT)
4.3.4 探索三角形全等的条件
复习回顾
新知探索
典例分析
课堂小结
作业布置
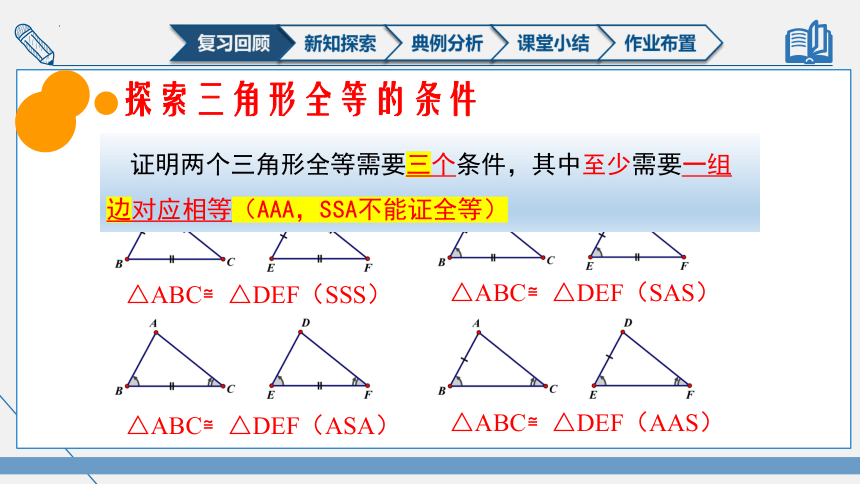
探索三角形全等的条件
你学过哪些方法可以判断两个三角形全等?
△ABC≌△DEF(SSS)
△ABC≌△DEF(SAS)
△ABC≌△DEF(ASA)
△ABC≌△DEF(AAS)
证明两个三角形全等需要三个条件,其中至少需要一组边对应相等(AAA,SSA不能证全等)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
《全等三角形综合复习》P8
例4如图,请添加两个条件,使得△ABC≌△ADE
(1)∠B=∠D , AB=AD ,得△ABC≌△ADE(ASA)
(2) , ,得△ABC≌△ADE( )
(3) , ,得△ABC≌△ADE( )
(4) , ,得△ABC≌△ADE( )
(5) , ,得△ABC≌△ADE( )
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索Rt三角形全等的条件
已知一个直角三角形两边分别为3cm,4cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
4cm
3cm
(1)4cm为直角边
(2)4cm为斜边
两边及夹角对应相等的两个三角形全等
斜边及一直角边对应相等的两个直角三角形全等
新知探索
复习回顾
典例分析
课堂小结
作业布置
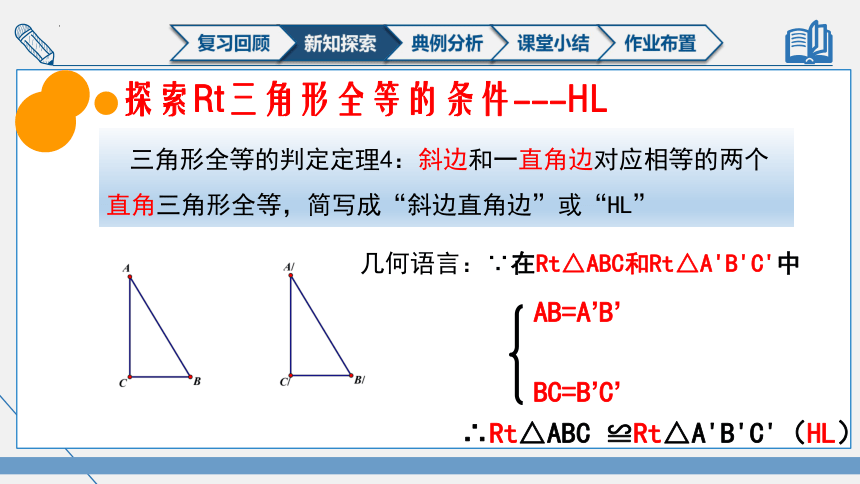
探索Rt三角形全等的条件---HL
三角形全等的判定定理4:斜边和一直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或“HL”
几何语言:∵在Rt△ABC和Rt△A'B'C'中
AB=A’B’
BC=B’C’
∴Rt△ABC ≌Rt△A'B'C'(HL)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
《全等三角形综合复习》P9
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
变式 已知AB⊥BD,CD⊥BD,且BE=DF,添一个条件使得△ABF ≌ △CDE
① ( HL );
② ( SAS );
③ ( AAS );
④ ( ASA );
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
例2 如图,AB∥CD,∠A=90°,AB=EC,BC=DE,BC与DE相交于点O.求证:DE⊥BC
变式:若将“BC=DE”改为“AC=CD”呢?
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P105
△AOD≌△ BOC(SAS) ;
由(1)得AD=BC, 结合OA+OC=OB+OD,DC=CD可证△ACD≌△ BDC(SSS) ;
由(1)得AD=BC, ∠A=∠B, 结合OA+OC=OB+OD可证△ACD≌△ BDC(SAS) ;
由(1)得AD=BC,∠A=∠B, 由OD=OC得∠OCD=∠ODC,可证△ACD≌△ BDC(AAS) ;
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P106
△ABE≌△ DCE ;
△ABC≌△ DCB 。
(AAS)
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P106
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件
三角形全等
已知两边
找第三边(SSS)
找夹角(SAS)
已知一边一角
找角(ASA或AAS)
找已知角的夹边(SAS)
已知两角
:找任意一边(ASA或AAS)
找直角(HL)
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
性质
全等三角形
全等三角形的对应边相等,对应角相等
判定条件
边边边(SSS)
角边角(ASA)
角角边(AAS)
边角边(SAS)
4.3.4 探索三角形全等的条件
复习回顾
新知探索
典例分析
课堂小结
作业布置
探索三角形全等的条件
你学过哪些方法可以判断两个三角形全等?
△ABC≌△DEF(SSS)
△ABC≌△DEF(SAS)
△ABC≌△DEF(ASA)
△ABC≌△DEF(AAS)
证明两个三角形全等需要三个条件,其中至少需要一组边对应相等(AAA,SSA不能证全等)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
《全等三角形综合复习》P8
例4如图,请添加两个条件,使得△ABC≌△ADE
(1)∠B=∠D , AB=AD ,得△ABC≌△ADE(ASA)
(2) , ,得△ABC≌△ADE( )
(3) , ,得△ABC≌△ADE( )
(4) , ,得△ABC≌△ADE( )
(5) , ,得△ABC≌△ADE( )
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索Rt三角形全等的条件
已知一个直角三角形两边分别为3cm,4cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
4cm
3cm
(1)4cm为直角边
(2)4cm为斜边
两边及夹角对应相等的两个三角形全等
斜边及一直角边对应相等的两个直角三角形全等
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索Rt三角形全等的条件---HL
三角形全等的判定定理4:斜边和一直角边对应相等的两个直角三角形全等,简写成“斜边直角边”或“HL”
几何语言:∵在Rt△ABC和Rt△A'B'C'中
AB=A’B’
BC=B’C’
∴Rt△ABC ≌Rt△A'B'C'(HL)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
例1 如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC=BD.求证:BC=AD.
《全等三角形综合复习》P9
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
变式 已知AB⊥BD,CD⊥BD,且BE=DF,添一个条件使得△ABF ≌ △CDE
① ( HL );
② ( SAS );
③ ( AAS );
④ ( ASA );
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索Rt三角形全等的条件
例2 如图,AB∥CD,∠A=90°,AB=EC,BC=DE,BC与DE相交于点O.求证:DE⊥BC
变式:若将“BC=DE”改为“AC=CD”呢?
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P105
△AOD≌△ BOC(SAS) ;
由(1)得AD=BC, 结合OA+OC=OB+OD,DC=CD可证△ACD≌△ BDC(SSS) ;
由(1)得AD=BC, ∠A=∠B, 结合OA+OC=OB+OD可证△ACD≌△ BDC(SAS) ;
由(1)得AD=BC,∠A=∠B, 由OD=OC得∠OCD=∠ODC,可证△ACD≌△ BDC(AAS) ;
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P106
△ABE≌△ DCE ;
△ABC≌△ DCB 。
(AAS)
典例分析
复习回顾
新知探索
课堂小结
作业布置
二次全等
《北师大》P106
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件
三角形全等
已知两边
找第三边(SSS)
找夹角(SAS)
已知一边一角
找角(ASA或AAS)
找已知角的夹边(SAS)
已知两角
:找任意一边(ASA或AAS)
找直角(HL)
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
性质
全等三角形
全等三角形的对应边相等,对应角相等
判定条件
边边边(SSS)
角边角(ASA)
角角边(AAS)
边角边(SAS)
同课章节目录
