7.1.2全概率公式(第1课时)课件(共14张PPT)
文档属性
| 名称 | 7.1.2全概率公式(第1课时)课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 768.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
7.1.2 全概率公式
(第1课时)
学习目标
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
1.条件概率
3.概率的乘法公式
【复习导入】
问题导学
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率. 下面, 再看一个求复杂事件概率的问题.
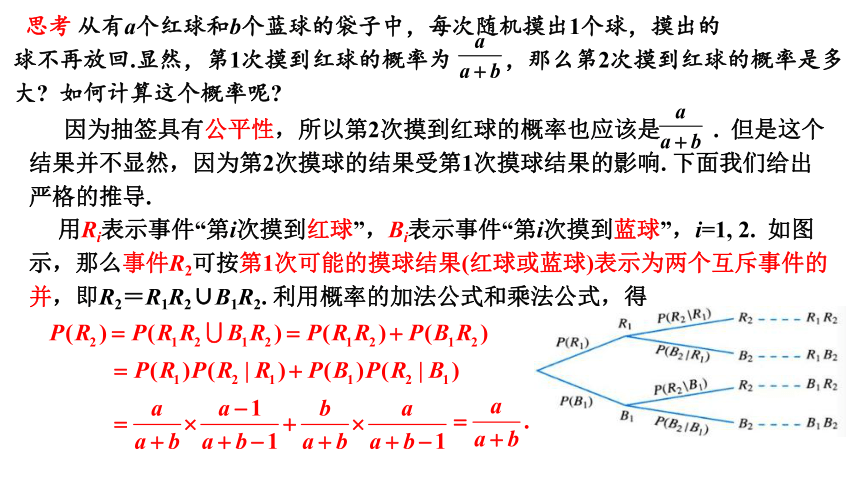
思考 从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的
球不再放回.显然,第1次摸到红球的概率为 ,那么第2次摸到红球的概率是多大 如何计算这个概率呢
因为抽签具有公平性,所以第2次摸到红球的概率也应该是 . 但是这个结果并不显然,因为第2次摸球的结果受第1次摸球结果的影响. 下面我们给出严格的推导.
用Ri表示事件“第i次摸到红球”,Bi表示事件“第i次摸到蓝球”,i=1, 2. 如图示,那么事件R2可按第1次可能的摸球结果(红球或蓝球)表示为两个互斥事件的并,即R2=R1R2∪B1R2. 利用概率的加法公式和乘法公式,得
上述过程采用的方法是: 按照某种标准,将一个复杂事件表示为
两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
全概率公式:
我们称上面的公式为全概率公式. 全概率公式是概率论中最基本的公式之一.
例4 某学校有 A,B两家餐厅,王同学第1天午餐时随机地选择一家
餐厅用餐. 如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8. 计算王同学第2天去A餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
【方法技巧】
全概率公式针对的是某一个过程中已知条件求出最后结果的概率,
解题步骤如下:
(1)找出条件事件里某一个完备事件组,分别命名为;
(2)命名目标的概率事件为事件;
(3)代入全概率公式求解.
【归纳总结】
解:
1. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题
完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
设A=“选到有思路的题”, B=“选到的题做对”, 则由全概率公式, 可得
【课本练习】课本P52 练习
例5 有 3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1) 任取一个零件,计算它是次品的概率;
(2) 如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
设B=“任取一个零件为次品”, Ai=“零件为第i台车床加工” (i=1, 2, 3), 则
解:
例5 有 3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1) 任取一个零件,计算它是次品的概率;
(2) 如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
(2)如果取到的零件是次品,计算它是第i(i=1, 2, 3)台车床加工的概率,
就是计算在B发生的条件下,事件Ai发生的概率,即
解:
2.某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间
的次品率为0.12,两个车间的成品都混合堆放在一个仓库,假设第一、二车间
生产的成品比例为2:3,今有一客户从成品仓库中随机提一台成品,则该产品
合格的概率是多少?
解:设“从仓库中随机提出的一台是合格品”,
“提出的一台是第车间生产的”().则有,
由题意知,,,,
由全概率公式得
7.1.2 全概率公式
(第1课时)
学习目标
1.结合古典概型,了解利用概率的加法公式和乘法公式推导出全概率公式的过程;
2.理解全概率公式的形式并会利用全概率公式计算概率;
3.了解贝叶斯公式以及公式的简单应用.
1.条件概率
3.概率的乘法公式
【复习导入】
问题导学
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法公式和乘法公式求其概率. 下面, 再看一个求复杂事件概率的问题.
思考 从有a个红球和b个蓝球的袋子中,每次随机摸出1个球,摸出的
球不再放回.显然,第1次摸到红球的概率为 ,那么第2次摸到红球的概率是多大 如何计算这个概率呢
因为抽签具有公平性,所以第2次摸到红球的概率也应该是 . 但是这个结果并不显然,因为第2次摸球的结果受第1次摸球结果的影响. 下面我们给出严格的推导.
用Ri表示事件“第i次摸到红球”,Bi表示事件“第i次摸到蓝球”,i=1, 2. 如图示,那么事件R2可按第1次可能的摸球结果(红球或蓝球)表示为两个互斥事件的并,即R2=R1R2∪B1R2. 利用概率的加法公式和乘法公式,得
上述过程采用的方法是: 按照某种标准,将一个复杂事件表示为
两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
全概率公式:
我们称上面的公式为全概率公式. 全概率公式是概率论中最基本的公式之一.
例4 某学校有 A,B两家餐厅,王同学第1天午餐时随机地选择一家
餐厅用餐. 如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8. 计算王同学第2天去A餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
【方法技巧】
全概率公式针对的是某一个过程中已知条件求出最后结果的概率,
解题步骤如下:
(1)找出条件事件里某一个完备事件组,分别命名为;
(2)命名目标的概率事件为事件;
(3)代入全概率公式求解.
【归纳总结】
解:
1. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题
完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
设A=“选到有思路的题”, B=“选到的题做对”, 则由全概率公式, 可得
【课本练习】课本P52 练习
例5 有 3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1) 任取一个零件,计算它是次品的概率;
(2) 如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
设B=“任取一个零件为次品”, Ai=“零件为第i台车床加工” (i=1, 2, 3), 则
解:
例5 有 3台车床加工同一型号的零件,第1台加工的次品率为6%,
第2,3台加工的次品率均为5%,加工出来的零件混放在一起,已知第1,2,3台车床加工的零件数分别占总数的25%,30%,45%.
(1) 任取一个零件,计算它是次品的概率;
(2) 如果取到的零件是次品,计算它是第i(i=1,2,3)台车床加工的概率.
(2)如果取到的零件是次品,计算它是第i(i=1, 2, 3)台车床加工的概率,
就是计算在B发生的条件下,事件Ai发生的概率,即
解:
2.某工厂有两个车间生产同型号家用电器,第一车间的次品率为0.15,第二车间
的次品率为0.12,两个车间的成品都混合堆放在一个仓库,假设第一、二车间
生产的成品比例为2:3,今有一客户从成品仓库中随机提一台成品,则该产品
合格的概率是多少?
解:设“从仓库中随机提出的一台是合格品”,
“提出的一台是第车间生产的”().则有,
由题意知,,,,
由全概率公式得
