4.1.1 认识三角形 课件(共16张PPT)2024-2025学年北师大版数学七年级下册
文档属性
| 名称 | 4.1.1 认识三角形 课件(共16张PPT)2024-2025学年北师大版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第四章 三角形
4.1.1 认识三角形
课堂导入
在我们日常生活中经常能看到三角形的影子.
减速慢行
注意儿童
前方村庄
新知探究
思考:观察图片,提出问题:
(1)你能从中找出四个不同的三角形吗?
(2)这些三角形有什么共同特点?
A
B
C
1.什么叫做三角形?
2.如何表示三角形?
3.三角形有哪些要素?
新知应用
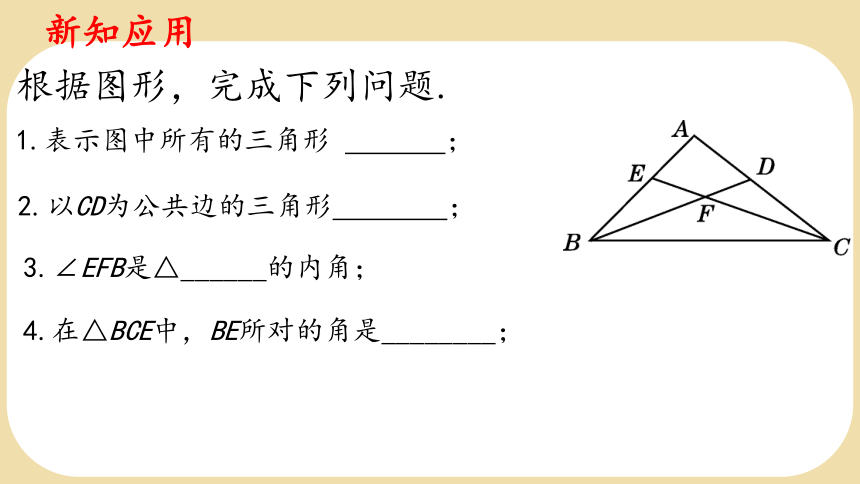
1.表示图中所有的三角形 ;
根据图形,完成下列问题.
2.以CD为公共边的三角形 ;
3.∠EFB是△______的内角;
4.在△BCE中,BE所对的角是________;
新知探究
三角形的三个内角有什么数量关系?
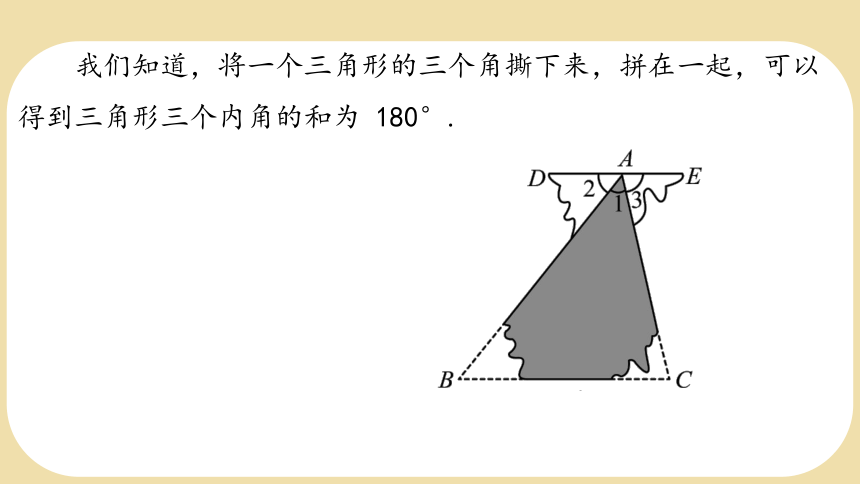
我们知道,将一个三角形的三个角撕下来,拼在一起,可以得到三角形三个内角的和为 180°.
小明只撕下三角形的一个角,也得到上面的结论,他的做法如下.
△ABC中的三个内角分别为∠1,∠2,∠3.将∠2撕下,按右图的方式拼摆,使∠2与∠1的顶点重合,∠2的一边与AB重合.
利用图,小明说明了三角形三个内角的和为 180°.你知道他是如何说明的吗
新知应用
例2 :如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于
( )
A.100° B.80° C.60° D.40°
下图中三角形被遮住的两个内角可能是什么角
下图中三角形被遮住的两个内角是什么角?
思考:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
钝角三角形
直角三角形
三个内角都是
锐角
有一个内角是
直角
有一个内角是
钝角
新知应用
例3:观察下面的三角形,其中哪些是锐角三角形,哪些是直角三角形,哪些是钝角三角形
① ② ③ ④ ⑤ ⑥ ⑦
A
B
C
新知应用
例4:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D. 则图中与∠B互余的角有( )
A.1个
B.2个
C.3个
D.4个
课堂小结
1.本节课我们学习了哪些内容?
2.通过本节课的学习,你有哪些收获?
第四章 三角形
4.1.1 认识三角形
课堂导入
在我们日常生活中经常能看到三角形的影子.
减速慢行
注意儿童
前方村庄
新知探究
思考:观察图片,提出问题:
(1)你能从中找出四个不同的三角形吗?
(2)这些三角形有什么共同特点?
A
B
C
1.什么叫做三角形?
2.如何表示三角形?
3.三角形有哪些要素?
新知应用
1.表示图中所有的三角形 ;
根据图形,完成下列问题.
2.以CD为公共边的三角形 ;
3.∠EFB是△______的内角;
4.在△BCE中,BE所对的角是________;
新知探究
三角形的三个内角有什么数量关系?
我们知道,将一个三角形的三个角撕下来,拼在一起,可以得到三角形三个内角的和为 180°.
小明只撕下三角形的一个角,也得到上面的结论,他的做法如下.
△ABC中的三个内角分别为∠1,∠2,∠3.将∠2撕下,按右图的方式拼摆,使∠2与∠1的顶点重合,∠2的一边与AB重合.
利用图,小明说明了三角形三个内角的和为 180°.你知道他是如何说明的吗
新知应用
例2 :如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于
( )
A.100° B.80° C.60° D.40°
下图中三角形被遮住的两个内角可能是什么角
下图中三角形被遮住的两个内角是什么角?
思考:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
钝角三角形
直角三角形
三个内角都是
锐角
有一个内角是
直角
有一个内角是
钝角
新知应用
例3:观察下面的三角形,其中哪些是锐角三角形,哪些是直角三角形,哪些是钝角三角形
① ② ③ ④ ⑤ ⑥ ⑦
A
B
C
新知应用
例4:如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D. 则图中与∠B互余的角有( )
A.1个
B.2个
C.3个
D.4个
课堂小结
1.本节课我们学习了哪些内容?
2.通过本节课的学习,你有哪些收获?
同课章节目录
