4.1.2认识三角形(第二课时)课件(共22张PPT) 2024--2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.1.2认识三角形(第二课时)课件(共22张PPT) 2024--2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 18:31:33 | ||
图片预览





文档简介
(共22张PPT)
4.1.2 认识三角形(第二课时)
新课引入
新知探索
典例分析
课堂小结
作业布置
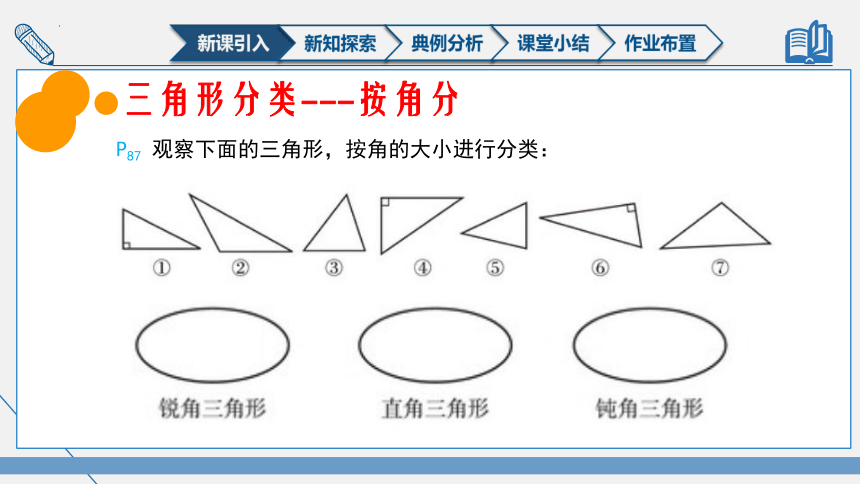
三角形分类---按角分
P87 观察下面的三角形,按角的大小进行分类:
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形分类---按边分
P88 观察下面的三角形,你能发现它们各自的边长之间有什么关系吗?
有两条边相等
三边都相等
三边各不相等
等腰三角形:两边相等的三角形
等边三角形(正三角形):三边都相等的三角形
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形分类---按边分
三角形
等腰三角形
等边三角形
三边各不相等的三角形: 不等边 三角形
等腰三角形
腰和底不相等的等腰三角形
等边三角形
三角形
不等边
(1)节日的晚上,房间内亮起了彩灯。如图装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说说你的理由。
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?为什么?与同伴进行交流。
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
思考·交流
三角形任意两边的和大于第三边.
新知探索
新课引入
典例分析
课堂小结
作业布置
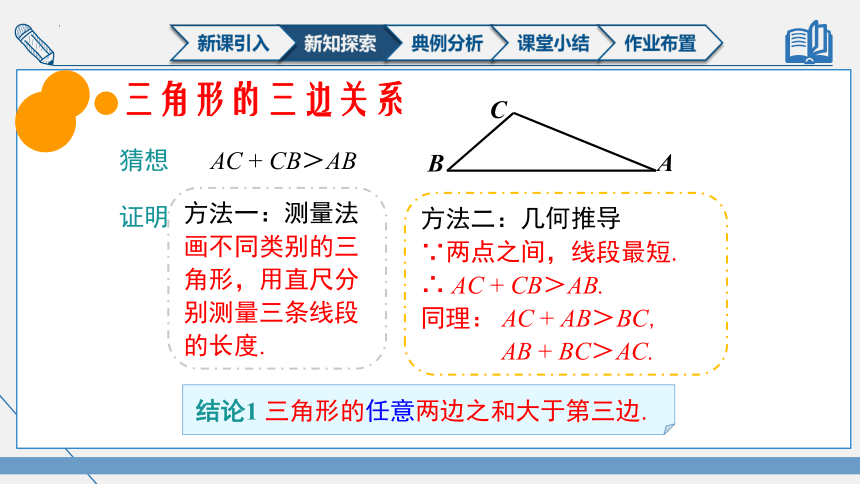
三角形的三边关系
猜想
AC + CB>AB
证明
方法二:几何推导
∵两点之间,线段最短.
∴ AC + CB>AB.
同理: AC + AB>BC,
AB + BC>AC.
方法一:测量法
画不同类别的三角形,用直尺分别测量三条线段的长度.
结论1 三角形的任意两边之和大于第三边.
A
B
C
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
a
b
c
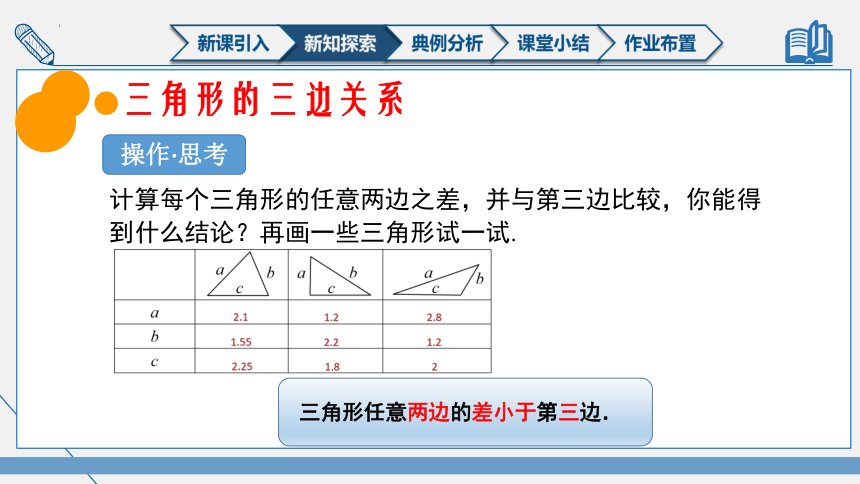
1、分别量出三个三角形的三边长度,并填人空格内.
a
b
c
a
b
c
a
b
c
操作·思考
2.1
1.55
2.25
1.2
2.2
1.8
2.8
1.2
2
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论?再画一些三角形试一试.
操作·思考
三角形任意两边的差小于第三边.
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
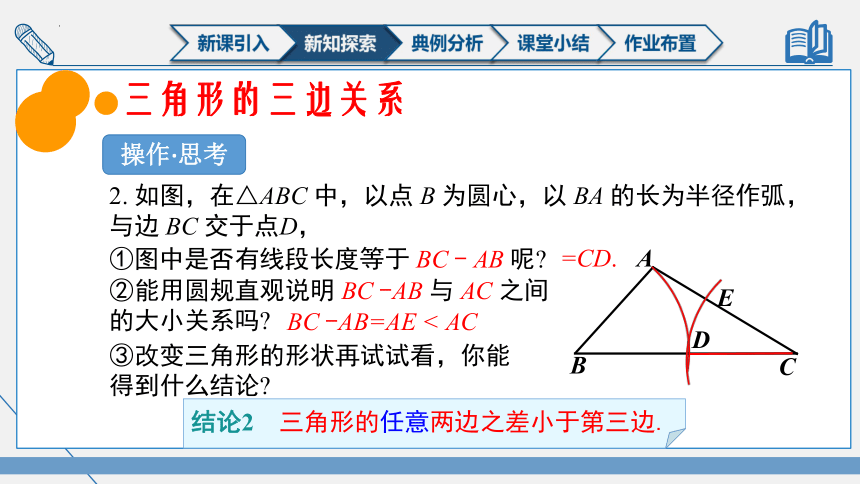
操作·思考
2. 如图,在△ABC 中,以点 B 为圆心,以 BA 的长为半径作弧,与边 BC 交于点D,
A
B
C
D
=CD.
③改变三角形的形状再试试看,你能
得到什么结论
②能用圆规直观说明 BC -AB 与 AC 之间
的大小关系吗
结论2 三角形的任意两边之差小于第三边.
BC -AB=AE < AC
E
①图中是否有线段长度等于 BC - AB 呢
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
BA+AC>BC
AC+CB>AB
CB+BA>CA
三角形任意两边的和大于第三边.
三角形任意两边的差小于第三边.
AC>BC-BA
CB>AB-AC
BA>CA-CB
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P93
三条线段能组成三角形,满足:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P89
例
有两根长度分别为5cm和8cm的木棒,能用一根2cm长的木棒与它们能摆成三角形吗 为什么 用长度为13cm的木棒呢
∵2+5=7<8,
∴不能构成三角形
又∵5+8=13
∴也不能构成三角形
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
三角形的第三边c范围:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P90
变式:如果第三边是奇数呢
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P117
变式:能组成三角形的概率是 。
典例分析
新课引入
新知探索
课堂小结
作业布置
等腰三角形的双解问题
(2)等腰三角形一边长9cm,另一边长4cm,它的第三边是多少 为什么
解:①当腰为4cm时,三边为4cm,4cm,9cm.
因为4+4<9,所以不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,所以三角形的第三边为9cm
典例分析
新课引入
新知探索
课堂小结
作业布置
2. 已知等腰三角形的两条边的长分别为5cm和8cm,求它的周长.
解:①当腰是5cm,底边是8cm时,能构成三角形,
则其周长为5+5+8=18(cm);
②当底边是5cm,腰是8cm时,能构成三角形,
则其周长为5+8+8=21(cm).
综上所述,这个三角形的周长为18cm或21cm.
等腰三角形的双解问题
典例分析
新课引入
新知探索
课堂小结
作业布置
2.已知一个等腰三角形的周长为18cm.
(1)若腰长是底边长的2倍,求各边长;
(2)若其中一边的长为4cm,求其他两边的长.
(2)①当等腰三角形的底边长为4cm 时,腰长为(18-4)÷2=7(cm).则等腰三角形的三边长分别4cm,7cm,7cm;
②当等腰三角形的腰长为4cm时,底边长为18-2×4=10(cm),则等腰三角形的三边长分别为4cm,4cm,10cm, 不能构成三角形.
综上所述,等腰三角形另外两边的长为7cm,7cm
解:(1)设底边长为xcm,则腰长为2xcm.
所以2x+2x+x=18.解得x=3.6.则2x=7.2.
所以这个等腰三角形的三边长分别为 3.6cm,7.2cm,7.2cm.
等腰三角形的双解问题
典例分析
新课引入
新知探索
课堂小结
作业布置
数形结合
已知a,b,c为△ABC 的三边长,b,c满足(b-2)2 +|c-3|=0,且a为方程|a-4|=2的解,判断△ABC的形状,并求△ABC的周长.
解:因为(b-2)2 +|c-3|=0,所以b-2=0,c-3=0,
解得b=2,c=3.
因为a为方程|a-4|=2的解,所以a-4=±2,
解得a=6或a=2.
因为a,b,c为△ABC的三边长,
所以a=6不合题意,舍去.
所以a=2.所以a=b=2,c=3.所以△ABC是等腰三角形,其周长为2+2+3=7.
典例分析
新课引入
新知探索
课堂小结
作业布置
已知a,b,c是△ABC的三边长,化简:|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
所以|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
数形结合
典例分析
新课引入
新知探索
课堂小结
作业布置
1.已知△ABC的三条边长分别为a,b,c,化简:|a-b-c|-|a+c-b|= __________ .
【解析】根据三角形的三边关系,得a-b-c<0,a+c-b>0,原式=-(a-b-c)-(a+c-b)= -a+b+c-a-c+b=2b-2a.故答案为2b-2a.
2b-2a
2.已知三角形的三边长分别是3,x,9,则化简|x-5|+|x-13|的结果是_______ .
8
【解析】因为三角形的三边长分别是3、x、9,所以60,x-13<0,所以|x-5|+|x-13|=x-5+13-x=8.故答案为8
数形结合
典例分析
新课引入
新知探索
课堂小结
作业布置
实际应用
补例 某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
A
B
C
D
P
P1
说明原因
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
三角形中边的关系
三角形
按边分类
三边各不相等的三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
4.1.2 认识三角形(第二课时)
新课引入
新知探索
典例分析
课堂小结
作业布置
三角形分类---按角分
P87 观察下面的三角形,按角的大小进行分类:
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形分类---按边分
P88 观察下面的三角形,你能发现它们各自的边长之间有什么关系吗?
有两条边相等
三边都相等
三边各不相等
等腰三角形:两边相等的三角形
等边三角形(正三角形):三边都相等的三角形
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形分类---按边分
三角形
等腰三角形
等边三角形
三边各不相等的三角形: 不等边 三角形
等腰三角形
腰和底不相等的等腰三角形
等边三角形
三角形
不等边
(1)节日的晚上,房间内亮起了彩灯。如图装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说说你的理由。
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?为什么?与同伴进行交流。
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
思考·交流
三角形任意两边的和大于第三边.
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
猜想
AC + CB>AB
证明
方法二:几何推导
∵两点之间,线段最短.
∴ AC + CB>AB.
同理: AC + AB>BC,
AB + BC>AC.
方法一:测量法
画不同类别的三角形,用直尺分别测量三条线段的长度.
结论1 三角形的任意两边之和大于第三边.
A
B
C
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
a
b
c
1、分别量出三个三角形的三边长度,并填人空格内.
a
b
c
a
b
c
a
b
c
操作·思考
2.1
1.55
2.25
1.2
2.2
1.8
2.8
1.2
2
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
计算每个三角形的任意两边之差,并与第三边比较,你能得到什么结论?再画一些三角形试一试.
操作·思考
三角形任意两边的差小于第三边.
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
操作·思考
2. 如图,在△ABC 中,以点 B 为圆心,以 BA 的长为半径作弧,与边 BC 交于点D,
A
B
C
D
=CD.
③改变三角形的形状再试试看,你能
得到什么结论
②能用圆规直观说明 BC -AB 与 AC 之间
的大小关系吗
结论2 三角形的任意两边之差小于第三边.
BC -AB=AE < AC
E
①图中是否有线段长度等于 BC - AB 呢
新知探索
新课引入
典例分析
课堂小结
作业布置
三角形的三边关系
BA+AC>BC
AC+CB>AB
CB+BA>CA
三角形任意两边的和大于第三边.
三角形任意两边的差小于第三边.
AC>BC-BA
CB>AB-AC
BA>CA-CB
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P93
三条线段能组成三角形,满足:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P89
例
有两根长度分别为5cm和8cm的木棒,能用一根2cm长的木棒与它们能摆成三角形吗 为什么 用长度为13cm的木棒呢
∵2+5=7<8,
∴不能构成三角形
又∵5+8=13
∴也不能构成三角形
如果一根木棒能与原来的两根木棒摆成三角形,那么它的长度取值范围是什么?
三角形的第三边c范围:
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P90
变式:如果第三边是奇数呢
典例分析
新课引入
新知探索
课堂小结
作业布置
三角形的三边关系
《北师大》P117
变式:能组成三角形的概率是 。
典例分析
新课引入
新知探索
课堂小结
作业布置
等腰三角形的双解问题
(2)等腰三角形一边长9cm,另一边长4cm,它的第三边是多少 为什么
解:①当腰为4cm时,三边为4cm,4cm,9cm.
因为4+4<9,所以不符合三角形的三边关系定理,此种情况舍去;
②当腰为9cm时,三边为4cm,9cm,9cm,
此时符合三角形的三边关系定理,所以三角形的第三边为9cm
典例分析
新课引入
新知探索
课堂小结
作业布置
2. 已知等腰三角形的两条边的长分别为5cm和8cm,求它的周长.
解:①当腰是5cm,底边是8cm时,能构成三角形,
则其周长为5+5+8=18(cm);
②当底边是5cm,腰是8cm时,能构成三角形,
则其周长为5+8+8=21(cm).
综上所述,这个三角形的周长为18cm或21cm.
等腰三角形的双解问题
典例分析
新课引入
新知探索
课堂小结
作业布置
2.已知一个等腰三角形的周长为18cm.
(1)若腰长是底边长的2倍,求各边长;
(2)若其中一边的长为4cm,求其他两边的长.
(2)①当等腰三角形的底边长为4cm 时,腰长为(18-4)÷2=7(cm).则等腰三角形的三边长分别4cm,7cm,7cm;
②当等腰三角形的腰长为4cm时,底边长为18-2×4=10(cm),则等腰三角形的三边长分别为4cm,4cm,10cm, 不能构成三角形.
综上所述,等腰三角形另外两边的长为7cm,7cm
解:(1)设底边长为xcm,则腰长为2xcm.
所以2x+2x+x=18.解得x=3.6.则2x=7.2.
所以这个等腰三角形的三边长分别为 3.6cm,7.2cm,7.2cm.
等腰三角形的双解问题
典例分析
新课引入
新知探索
课堂小结
作业布置
数形结合
已知a,b,c为△ABC 的三边长,b,c满足(b-2)2 +|c-3|=0,且a为方程|a-4|=2的解,判断△ABC的形状,并求△ABC的周长.
解:因为(b-2)2 +|c-3|=0,所以b-2=0,c-3=0,
解得b=2,c=3.
因为a为方程|a-4|=2的解,所以a-4=±2,
解得a=6或a=2.
因为a,b,c为△ABC的三边长,
所以a=6不合题意,舍去.
所以a=2.所以a=b=2,c=3.所以△ABC是等腰三角形,其周长为2+2+3=7.
典例分析
新课引入
新知探索
课堂小结
作业布置
已知a,b,c是△ABC的三边长,化简:|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
所以|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
数形结合
典例分析
新课引入
新知探索
课堂小结
作业布置
1.已知△ABC的三条边长分别为a,b,c,化简:|a-b-c|-|a+c-b|= __________ .
【解析】根据三角形的三边关系,得a-b-c<0,a+c-b>0,原式=-(a-b-c)-(a+c-b)= -a+b+c-a-c+b=2b-2a.故答案为2b-2a.
2b-2a
2.已知三角形的三边长分别是3,x,9,则化简|x-5|+|x-13|的结果是_______ .
8
【解析】因为三角形的三边长分别是3、x、9,所以6
数形结合
典例分析
新课引入
新知探索
课堂小结
作业布置
实际应用
补例 某地有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
A
B
C
D
P
P1
说明原因
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
三角形中边的关系
三角形
按边分类
三边各不相等的三角形
等腰三角形(包括等边三角形)
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
同课章节目录
