4.3.3探索三角形全等的条件(SAS) 课件 (共20张PPT)2024--2025学年北师大版七年级数学下册
文档属性
| 名称 | 4.3.3探索三角形全等的条件(SAS) 课件 (共20张PPT)2024--2025学年北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 18:36:18 | ||
图片预览




文档简介
(共20张PPT)
4.3.3 探索三角形全等的条件(SAS)
复习回顾
新知探索
典例分析
课堂小结
作业布置
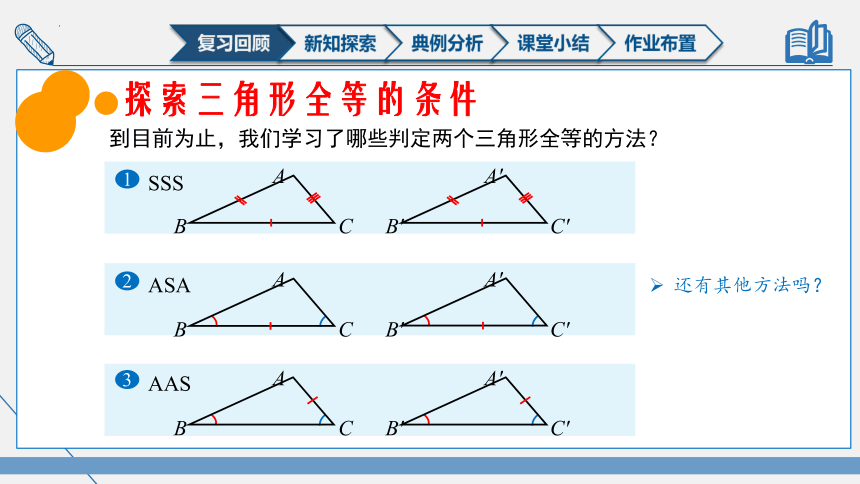
探索三角形全等的条件
到目前为止,我们学习了哪些判定两个三角形全等的方法?
A
B
C
A'
B'
C'
3
AAS
A
B
C
A'
B'
C'
1
SSS
A
B
C
A'
B'
C'
2
ASA
还有其他方法吗?
复习回顾
新知探索
典例分析
课堂小结
作业布置
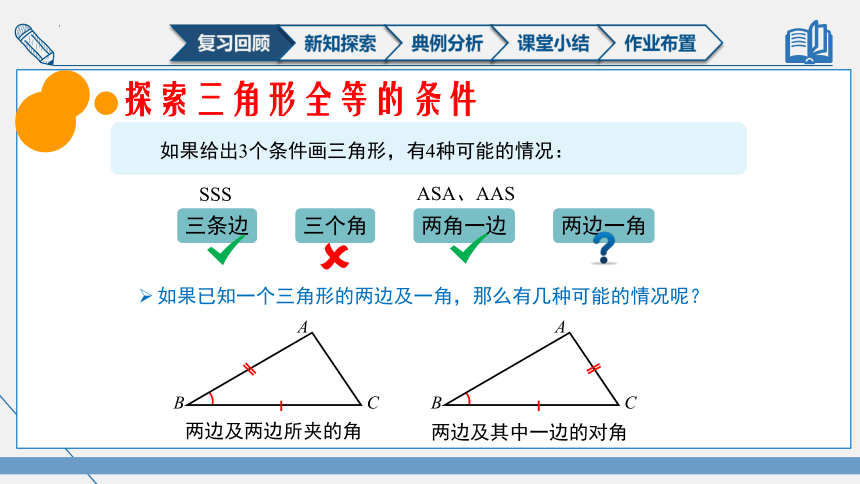
探索三角形全等的条件
如果给出3个条件画三角形,有4种可能的情况:
三个角
两角一边
三条边
两边一角
SSS
如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
ASA、AAS
A
B
C
两边及两边所夹的角
A
B
C
两边及其中一边的对角
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
新知探索
复习回顾
典例分析
课堂小结
作业布置
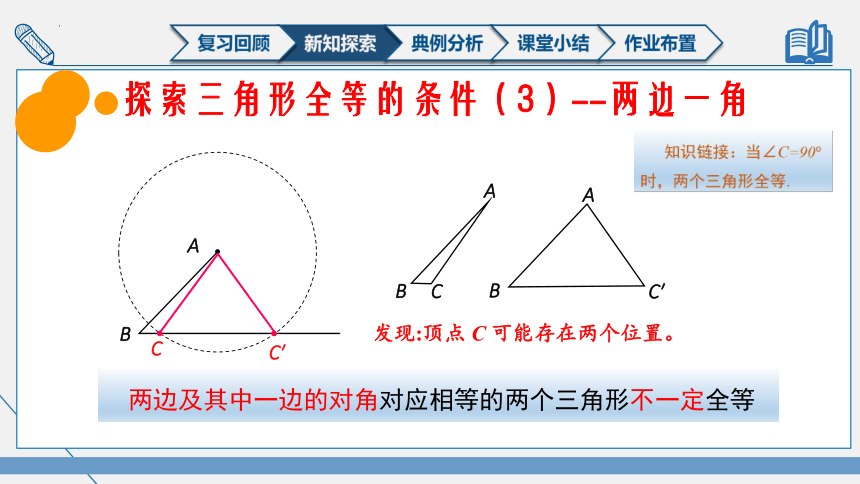
探索三角形全等的条件(3)--两边一角
教材P103
新知探索
复习回顾
典例分析
课堂小结
作业布置
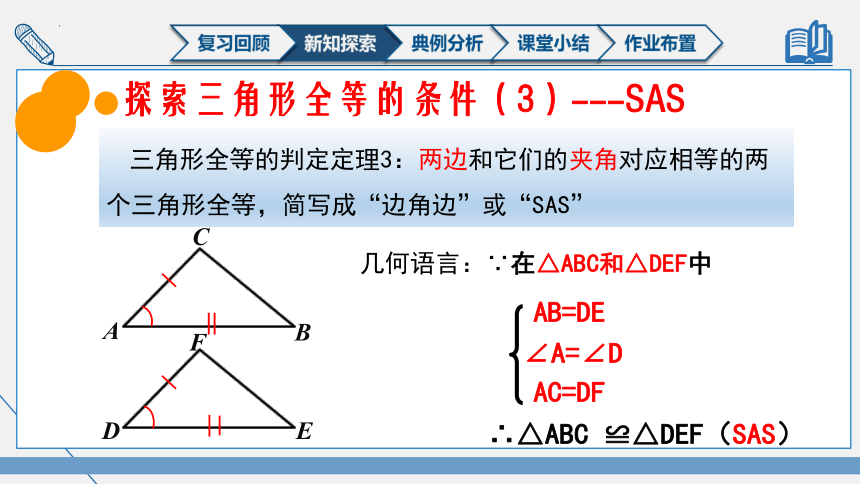
探索三角形全等的条件(3)---SAS
三角形全等的判定定理3:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
几何语言:∵在△ABC和△DEF中
AB=DE
∠A=∠D
AC=DF
∴△ABC ≌△DEF(SAS)
A
B
C
D
E
F
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
教材P104
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
A
B
C
C′
A
B
C
A
B
C′
发现:顶点 C 可能存在两个位置。
两边及其中一边的对角对应相等的两个三角形不一定全等
知识链接:当∠C=90时,两个三角形全等.
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件
两个三角形全等的判定:
SSS,ASA,AAS,SAS
(AAA和SSA不能证全等)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
练习:如图,在△ABC与△DEF中,已知∠A=∠D,AB=DE,增加一个什么条件就可以判定这两个三角形全等?
C
A
B
F
D
E
角
边
∠A=∠D
AB=DE
AC=DF
∠B=∠E
∠C=∠F
SAS
ASA
AAS
如果增加条件BC=EF,能判定这两个三角形全等吗?为什么?
SSA不能判定两个三角形全等.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
ASA
SAS
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
2. 如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC. 固定住长木棍,转动短木棍,得到△ABD. 这个实验说明了什么?可得到什么结论?
解:△ABC和△ABD满足AB=AB,∠B=∠B,AC=AD,但它们并不全等.
结论:两边分别相等且其中一组等边的对角
相等的两个三角形不一定全等;
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例1:如图点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,是判断CD与AB的关系,并证明你的结论。
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
1. 如图,已知点E在AB上,AC=AD,∠CAB=∠DAB,则图中共有 3 对全等三角形.
3
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例2 如图,已知点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,则“AB=AC”成立吗?说明你的理由.(用两种方法)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件(3)---SAS
补例3 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)是判断BD与CE的关系,并证明。
(2)若如图2放置,上面的结论还成立吗?请简单说明理由.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
如图,已知E是BC的中点,DE平分∠ADC,DE⊥AE,
试说明:AD=AB+CD.
解:在DA上截取DF=DC,连接EF.
∵DE平分∠ADC,
∴∠CDE=∠FDE.
在△CDE和△FDE中,
∴△CDE≌△FDE(SAS).
∴CE=FE,∠CED=∠FED.
又∵E是BC的中点,
∴CE=BE.
∴FE=BE.
由DE⊥AE,
得∠AEF+∠DEF=90°,∠AEB+∠CED=90°.
∴∠AEF=∠AEB.
在△AEF和△AEB中,
∴△AEF≌△AEB(SAS).
∴AF=AB. 则AD=AF+DF=AB+CD.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例4 如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,求证:AD=DC
新知探索
复习回顾
典例分析
课堂小结
作业布置
实际应用
《北师大》P104随堂练习
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
两边和其中一边的对角分别相等的两个三角形不一定全等.
注意:
两边及其夹角分别相等的两个三角形全等.
三角形全等的判定-SAS:
判定两个三角形全等的方法总结:
ASA
AAS
SAS
SSS
三
角
形
全
等
的
判
定
|
SAS
4.3.3 探索三角形全等的条件(SAS)
复习回顾
新知探索
典例分析
课堂小结
作业布置
探索三角形全等的条件
到目前为止,我们学习了哪些判定两个三角形全等的方法?
A
B
C
A'
B'
C'
3
AAS
A
B
C
A'
B'
C'
1
SSS
A
B
C
A'
B'
C'
2
ASA
还有其他方法吗?
复习回顾
新知探索
典例分析
课堂小结
作业布置
探索三角形全等的条件
如果给出3个条件画三角形,有4种可能的情况:
三个角
两角一边
三条边
两边一角
SSS
如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
ASA、AAS
A
B
C
两边及两边所夹的角
A
B
C
两边及其中一边的对角
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
教材P103
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)---SAS
三角形全等的判定定理3:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
几何语言:∵在△ABC和△DEF中
AB=DE
∠A=∠D
AC=DF
∴△ABC ≌△DEF(SAS)
A
B
C
D
E
F
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
教材P104
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件(3)--两边一角
A
B
C
C′
A
B
C
A
B
C′
发现:顶点 C 可能存在两个位置。
两边及其中一边的对角对应相等的两个三角形不一定全等
知识链接:当∠C=90时,两个三角形全等.
新知探索
复习回顾
典例分析
课堂小结
作业布置
探索三角形全等的条件
两个三角形全等的判定:
SSS,ASA,AAS,SAS
(AAA和SSA不能证全等)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
练习:如图,在△ABC与△DEF中,已知∠A=∠D,AB=DE,增加一个什么条件就可以判定这两个三角形全等?
C
A
B
F
D
E
角
边
∠A=∠D
AB=DE
AC=DF
∠B=∠E
∠C=∠F
SAS
ASA
AAS
如果增加条件BC=EF,能判定这两个三角形全等吗?为什么?
SSA不能判定两个三角形全等.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
ASA
SAS
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
2. 如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC. 固定住长木棍,转动短木棍,得到△ABD. 这个实验说明了什么?可得到什么结论?
解:△ABC和△ABD满足AB=AB,∠B=∠B,AC=AD,但它们并不全等.
结论:两边分别相等且其中一组等边的对角
相等的两个三角形不一定全等;
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例1:如图点C、F、E、B在一条直线上,∠CFD=∠BEA,CE=BF,DF=AE,是判断CD与AB的关系,并证明你的结论。
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
1. 如图,已知点E在AB上,AC=AD,∠CAB=∠DAB,则图中共有 3 对全等三角形.
3
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例2 如图,已知点D、E在BC上,且BD=CE,AD=AE,∠1=∠2,则“AB=AC”成立吗?说明你的理由.(用两种方法)
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件(3)---SAS
补例3 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)是判断BD与CE的关系,并证明。
(2)若如图2放置,上面的结论还成立吗?请简单说明理由.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
如图,已知E是BC的中点,DE平分∠ADC,DE⊥AE,
试说明:AD=AB+CD.
解:在DA上截取DF=DC,连接EF.
∵DE平分∠ADC,
∴∠CDE=∠FDE.
在△CDE和△FDE中,
∴△CDE≌△FDE(SAS).
∴CE=FE,∠CED=∠FED.
又∵E是BC的中点,
∴CE=BE.
∴FE=BE.
由DE⊥AE,
得∠AEF+∠DEF=90°,∠AEB+∠CED=90°.
∴∠AEF=∠AEB.
在△AEF和△AEB中,
∴△AEF≌△AEB(SAS).
∴AF=AB. 则AD=AF+DF=AB+CD.
典例分析
复习回顾
新知探索
课堂小结
作业布置
探索三角形全等的条件
补例4 如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,求证:AD=DC
新知探索
复习回顾
典例分析
课堂小结
作业布置
实际应用
《北师大》P104随堂练习
课堂小结
作业布置
复习回顾
新知讲解
典例分析
课堂小结
两边和其中一边的对角分别相等的两个三角形不一定全等.
注意:
两边及其夹角分别相等的两个三角形全等.
三角形全等的判定-SAS:
判定两个三角形全等的方法总结:
ASA
AAS
SAS
SSS
三
角
形
全
等
的
判
定
|
SAS
同课章节目录
