人教新课标A版必修3数学2.2.1用样本的频率分布估计总体同步检测
文档属性
| 名称 | 人教新课标A版必修3数学2.2.1用样本的频率分布估计总体同步检测 |
|
|
| 格式 | doc | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-06 11:38:33 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
2.2.1用样本的频率分布估计总体同步检测
一、选择题
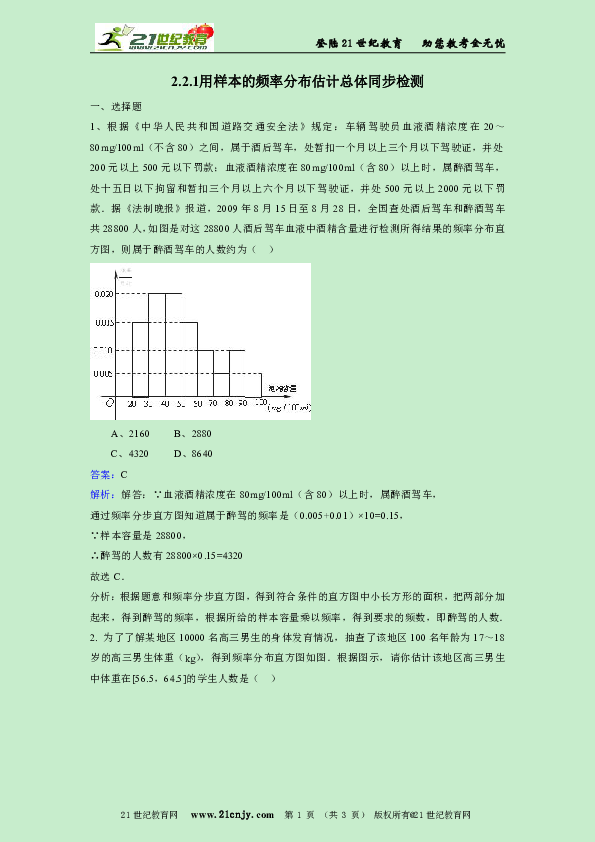
1、根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车,处暂扣一个月以上三个月以下驾驶证,并处200元以上500元以下罚款;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和暂扣三个月以上六个月以下驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
A、2160 B、2880
C、4320 D、8640
答案:C
解析:解答:∵血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,
通过频率分步直方图知道属于醉驾的频率是(0.005+0.01)×10=0.15,
∵样本容量是28800,
∴醉驾的人数有28800×0.15=4320
故选C.
分析:根据题意和频率分步直方图,得到符合条件的直方图中小长方形的面积,把两部分加起来,得到醉驾的频率,根据所给的样本容量乘以频率,得到要求的频数,即醉驾的人数.
2. 为了了解某地区10000名高三男生的身体发育情况,抽查了该地区100名年龄为17~18岁的高三男生体重(kg),得到频率分布直方图如图.根据图示,请你估计该地区高三男生中体重在[56.5,64.5]的学生人数是( )
( http: / / www.21cnjy.com )
A、40 B、400
C、4000 D、4400
答案:C
解析:解答:高三男生中体重在[56.5,64.5]的学生的频率
(0.03+0.05+0.05+0.07)×2=0.4
∴该地区高三男生中体重在[56.5,64.5]的学生人数是
0.4×10000=4000
故选C
分析:求出[56.,64.5]的纵坐标和乘以每个矩形的宽得到在[56.5,64.5]的学生的频率,利用频率乘以样本容量得到该地区高三男生中体重在[56.5,64.5]的学生人数.
3. 如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若80
分以上为优秀,根据图形信息可知:这次考试的优秀率为( )
A、25% B、30%
C、35% D、40%
答案:B
解析:解答:0.025×10+0.005×10=0.3
所以这次考试的优秀率为30%
故选B
分析:利用大于80的两个矩形的纵坐标乘以组距10的和,得到的是这次考试的优秀率.
4. 将一组数据分成6组,其中前3组的频率之和是0.65,后两组的频率之和是0.32,那么第四小组的频率是 ( )
A、0.02 B、0.01
C、0.03 D、0.04
答案:C
解析:解答:由题意得:第四小组的频率是:
1﹣0.65﹣0.32=0.03.
故选C.
分析:根据各小组频率之和等于1计算第四小组的频率是1﹣0.65﹣0.32=0.03.
5. 为了了解某市高三毕业生升学考试中数学成绩的情况从参加考试的学生中随机地抽查了1000名学生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
A、总体指的是该市参加升学考试的全体学生
B、个体指的是1000名学生中的每一名学生
C、样本容量指的是1000名学生
D、样本是指1000名学生的数学升学考试成绩
答案:D
解析:解答:本题的总体是该市高三毕业生的数学成绩,
个体是指每名学生的成绩,
样本容量是1000,
了解某市高三毕业生升学考试中学生的数学成绩的情况,
因此样本是指1000名学生的数学成绩,
故选D.
分析:是了解某市高三毕业生升学考试中学生的数学成绩的情况,所要了解的是这组学生的数学成绩,看出总体是所有学生的数学成绩,个体是一个学生的数学成绩,样本容量是1000.
6. 为了解湖中鱼的多少,某人在湖中打了一网鱼,共m条,做上记号后放入湖中,数日后又打了一网鱼,共n条,其中k条鱼有记号,估计湖中有鱼( )
A、条 B、条
C、m条 D、无法估计
答案:B
解析:解答:∵做记号的鱼已经完全分散开了,是分布均匀的.
∴湖中每个个体被抽到的机会都相等,
∴,
∴x=.
故选B.
分析:依据湖中每个个体被抽到的机会都相等列式解决.
7. 为了了解某地参加计算机水平测试的5000名学生的成绩,从中抽取了200名学生的成绩进行统计分析,在这个问题中,下列说法正确的是( )
A、总体指的是参加计算机水平测试的5000名学生
B、个体指的是5000名学生中的每一个学生
C、样本容量指的是抽取的200名学生
D、样本指的是抽取的200名学生的成绩
答案:D
解析:解答:总体指的是参加计算机水平测试的5000名学生的成绩,所以A错;
个体指的是5000名学生中的每一个学生的成绩,所以B错;
样本容量指的是抽取的200,所以C错;
样本指的是抽取的200名学生的成绩正确,所以D对;
故选D.
分析:本题考查的是确定总体.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考查的对象,考查对象是某地区初中毕业生参加中考的数学成绩,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
8. 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示,时速在[50,60)的汽车大约有( )
( http: / / www.21cnjy.com )
A、30辆 B、60辆
C、300辆 D、600辆
答案:D
解析:解答:∵有频率分步直方图可以看出
在[50,60)之间的频率是0.03×10=0.3,
∴时速在[50,60)的汽车大约有2000×0.3=600
故选D.
分析:根据频率分步直方图可以看出在[50,60)之间的小长方形的长和宽,做出对应的频率,用频率乘以样本容量得到结果.
9. 为了了解商场某日旅游鞋的销售情况,抽取了部分顾客购鞋的尺寸,将所得的数据整理后,画出频率分布直方图如图.已知中从左至右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分别为0.175和0.075,第二小组的频数为10,则抽取的顾客人数是( )
A、80 B、60
C、40 D、100
答案:C
解析:解答:由题意得:第4小组与第5小组的频率分别为0.175和0.075,
所以前3组的频率和为0.75.
又因为从左至右前3个小组的频率之比为1:2:3,
所以从左至右第2个小组的频率为:0.25.
因为第二小组的频数为10,
所以抽取的顾客人数是=40人.
故选C.
分析:有第四组与第五组的频率和得到前3组的频率和,又根据前三组的频率之比即可得到第二组的频率,结合第二组的频数可得抽取的顾客人数.
10. 某地一种植物一年生长的高度如下表:
( http: / / www.21cnjy.com )
则该植物一年生长在[30,40)内的频率是( )
A、0.80 B、0.65
C、0.40 D、0.25
答案:C
解析:解答:根据频率分布表可知样本容量是20+30+80+40+30,
在[30,40)这组数据中频数是80,
∴由频率的定义得80÷(20+30+80+40+30)=0.40.
故选C.
分析:根据所给的频率分布表看出这组数据的样本容量和落在所要求的范围的频数,根据样本容量,频数和频率之间的关系得到要求的结果.
11. 总体已经分成A,B,C三层,A,B,C三层个体数之比为2:3:5,现从总体中抽取容量为20的一个样本,已知A层中用简单随机抽样抽取样本时,甲被抽到的概率为,则总体的个体个数为( )
A、40 B、80
C、120 D、160
答案:B
解析:解答:∵现从总体中抽取容量为20的一个样本,
甲被抽到的概率为,
∴在整个抽样过程中每个个体被抽到的概率是
∴总体的个体个数为=80
故选B.
分析:根据现从总体中抽取容量为20的一个样本,个体甲被抽到的概率为,得到在整个抽样过程中每个个体被抽到的概率是,根据频率,频数和样本容量之间的关系得到结果.
12. 如图是某城市100位居民去年的月均用水量 (单位:t)的频率分布直方图,月均用水量在区间[1.5,2.5)的居民大约有( )
A、37位 B、40位
C、47位 D、52位
答案:C
解析:解答:由频率分布直方图月均用水量在区间[1.5,2)的频率为0.45×0.5=0.225.月均用水量在区间[2,2.5)的居民的频率 为0.50×0,5=0.25.
月均用水量在区间[1.5,,2.5)的居民的频数大约为(0.225+0.25)×100=47
故选C.
分析:先根据频率分布直方图求出月均用水量在区间[1.5,2),[2,2.5)的居民的频率.再求出居民的大约数.
二、填空题
13. 对某学校n名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为64人,则n= .
( http: / / www.21cnjy.com )
答案:400
解析:解答:体重在75kg以上的学生的频率为:0.032×5=0.16
所以体重在75kg以上的同学的人数为:n×0.16=64, n=400
故答案为:400.
分析:由频率分布直方图计算出体重在75kg以上的学生的频率,再利用频率和样本容量的关系计算即可.
14. 某校在学生的一次百米跑测试成绩中抽取50名学生的成绩进行统计,其频率分布直方图如图所示,则成绩小于17秒的学生人数为 .
答案:45
解析:解答:由频率分布直方图知,成绩小于17秒的频率为:
(0.02+0.18+0.36+0.34)×1=0.9.
所以成绩小于17秒的学生人数为0.9×50=45.
故答案为45.
分析:由频率分布直方图得到成绩小于17秒的频率;利用频数等于频率乘以样本容量,求出成绩小于17秒的学生人数.
15. 某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),把其中不低于50 分的分成五段[50,60),[60,70),[70,80),[80,90),[90,100]然后画出如下图的部分频率分布直方图.观察图形的信息,可知数学成绩低于50分的学生有 人;估计这次考试数学学科的及格率(60分及以上为及格)为 ;
( http: / / www.21cnjy.com )
答案:6|75%
解析:解答:由图可知,成绩在[50,60)的频率为0,015×10=0.15,成绩在[60,70)的频率为0.015×10=0.15,
成绩在[70,80)的频率为0.030×10=0.3,成绩在[80,90)的频率为0.025×10=0.25,
成绩在[90,100]的频率为0.005×10=0.05,
∴成绩不低于50 分的频率为0.15+0.15+0.3+0.25+0.05=0.9,成绩不低于60分的频率为0.15+0.3+0.25+0.05=0.75
∴成绩低于50分的频率为为1﹣0.9=0.1
∵共有60名学生,∴成绩低于50分的学生数为60×0.1=6,这次考试数学学科的及格率为75%.
故答案为6;75%
分析:先根据频率分布直方图,求出每段的频率,再计算出成绩低于50分的频率和成绩不低于60分的频率,则成绩低于50分的学生数就是它的频率乘以学生总数,这次考试数学学科的及格率就是成绩不低于60分的频率.
16. 从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:
则成绩在79.5~89.5这一组的频率为 .
( http: / / www.21cnjy.com )答案:0.25
解析:解答:∵每小组的频率=,
由频率的意义可知,
∴成绩在79.5~89.5这一组的频率
=0.025×10=0.25.
故填:0.25.
分析:根据直方图中79.5~89.5这一组的高度及频率的计算公式,可得成绩在79.5~89.5这一组的频率,进而可得答案.
17. 某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为 人.
答案:30
解析:解答:∵这100名同学中学习时间在6~8小时外的频率为
(0.04+0.12+0.14+0.05)×2=0..7
∴这100名同学中学习时间在6~8小时内为1﹣0.7=0.3
∴这100名同学中学习时间在6~8小时内的同学为100×0.3=30
故答案为:30
分析:利用频率分布直方图中,频率等于纵坐标乘以组距,求出在6~8小时外的频率;利用频率和为1,求出在6~8小时内的频率;利用频数等于频率乘以样本容量,求出这100名同学中学习时间在6~8小时内的同学的人数.
18. 某高级中学共有学生3000名,各年级男、女生人数如下表:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.现对各年级用分层抽样的方法在全校抽取300名学生,则应在高三年级抽取 名学生.
( http: / / www.21cnjy.com )
答案:99
解析:解答:∵抽到高二年级女生的概率是0.17,
∴高二年级女生有0.17×3000=510,
∴高三年级共有3000﹣523﹣487﹣490﹣510=990,
∵对各年级用分层抽样的方法在全校抽取300名学生,
∴每个学生被抽到的概率是,
∴应在高三抽取0.1×990=99
故答案为:99
分析:根据要在高二女生中抽取一个人的概率,做出高二女生的人数,用所有的人数减去高一和高二的人数,得到高三共有的人数,根据要抽取的人数和总体数,求出每个个体被抽到的概率,乘以高三的人数,得到结果.
三、解答题
19. 某学校随机抽取部分新生调查其上学 ( http: / / www.21cnjy.com / )路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(1)求直方图中x的值;
答案:解:由(x+0.0125+0.0065+0.003×2)×20=1,
解得x=0.025;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
答案:解:上学所需时间不少于40的学生的频率为:(0.0065+0.003×2)×20=0.25,
估计学校1000名新生中有:1000×0.25=250,
答:估计学校1000名新生中有250名学生可以申请住宿.
解析:分析:(1)根据频率分布直方图可以得到组距,而频率分布直方图的纵坐标与组距之积为频率,各组频率之和为1即可得到x的值.(2)根据频率分布直方图求出上学路上所需时间不少于60分钟的学生的频率,频率乘以总人数即可得到可以留宿学生的人数
20. 某校为了解毕业班学业水平考试学生的数 ( http: / / www.21cnjy.com )学考试情况,抽取了该校100名学生的数学成绩,将所有数据整理后,画出了样频率分布直方图(所图所示),若第1组、第9组的频率各为x.
(1) 求x的值,并估计这次学业水平考试数学成绩的平均数;
答案:解:
=0.03
由图可估计样本平均数=0.03×(62.5+102.5)+5×(0.012×67.5+0.012×72.5+0.024×77.5
+0.020×82.5+0.054×87.5+0.036×92.5+0.030×97.5)
=85.
(2)若全校有1500名学生参加了此次考试,估计成绩在[80,100)分内的人数.
答案:解:由图可知样本数据在[80,100)分内的频率为(0.02+0.054+0.036+0.03)×5=0.7,
则可以估计此次考试中成绩在[80,100)内的人数为
1500×0.7=1050(人).
( http: / / www.21cnjy.com )
解析:分析:(1)根据所以频率的和为1,求x的值,用每一组的平均值乘以改组的频率,相加即得所求的这次学业水平考试数学成绩的平均数的估算值,(2)由图可知样本数据在[80,100)分内的频率,用全校的总人数乘以这个频率,即可求得此次考试中成绩在[80,100)分内的人数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 12 页 (共 12 页) 版权所有@21世纪教育网
2.2.1用样本的频率分布估计总体同步检测
一、选择题
1、根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml(不含80)之间,属于酒后驾车,处暂扣一个月以上三个月以下驾驶证,并处200元以上500元以下罚款;血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,处十五日以下拘留和暂扣三个月以上六个月以下驾驶证,并处500元以上2000元以下罚款.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
A、2160 B、2880
C、4320 D、8640
答案:C
解析:解答:∵血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车,
通过频率分步直方图知道属于醉驾的频率是(0.005+0.01)×10=0.15,
∵样本容量是28800,
∴醉驾的人数有28800×0.15=4320
故选C.
分析:根据题意和频率分步直方图,得到符合条件的直方图中小长方形的面积,把两部分加起来,得到醉驾的频率,根据所给的样本容量乘以频率,得到要求的频数,即醉驾的人数.
2. 为了了解某地区10000名高三男生的身体发育情况,抽查了该地区100名年龄为17~18岁的高三男生体重(kg),得到频率分布直方图如图.根据图示,请你估计该地区高三男生中体重在[56.5,64.5]的学生人数是( )
( http: / / www.21cnjy.com )
A、40 B、400
C、4000 D、4400
答案:C
解析:解答:高三男生中体重在[56.5,64.5]的学生的频率
(0.03+0.05+0.05+0.07)×2=0.4
∴该地区高三男生中体重在[56.5,64.5]的学生人数是
0.4×10000=4000
故选C
分析:求出[56.,64.5]的纵坐标和乘以每个矩形的宽得到在[56.5,64.5]的学生的频率,利用频率乘以样本容量得到该地区高三男生中体重在[56.5,64.5]的学生人数.
3. 如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,若80
分以上为优秀,根据图形信息可知:这次考试的优秀率为( )
A、25% B、30%
C、35% D、40%
答案:B
解析:解答:0.025×10+0.005×10=0.3
所以这次考试的优秀率为30%
故选B
分析:利用大于80的两个矩形的纵坐标乘以组距10的和,得到的是这次考试的优秀率.
4. 将一组数据分成6组,其中前3组的频率之和是0.65,后两组的频率之和是0.32,那么第四小组的频率是 ( )
A、0.02 B、0.01
C、0.03 D、0.04
答案:C
解析:解答:由题意得:第四小组的频率是:
1﹣0.65﹣0.32=0.03.
故选C.
分析:根据各小组频率之和等于1计算第四小组的频率是1﹣0.65﹣0.32=0.03.
5. 为了了解某市高三毕业生升学考试中数学成绩的情况从参加考试的学生中随机地抽查了1000名学生的数学成绩进行统计分析,在这个问题中,下列说法正确的是( )
A、总体指的是该市参加升学考试的全体学生
B、个体指的是1000名学生中的每一名学生
C、样本容量指的是1000名学生
D、样本是指1000名学生的数学升学考试成绩
答案:D
解析:解答:本题的总体是该市高三毕业生的数学成绩,
个体是指每名学生的成绩,
样本容量是1000,
了解某市高三毕业生升学考试中学生的数学成绩的情况,
因此样本是指1000名学生的数学成绩,
故选D.
分析:是了解某市高三毕业生升学考试中学生的数学成绩的情况,所要了解的是这组学生的数学成绩,看出总体是所有学生的数学成绩,个体是一个学生的数学成绩,样本容量是1000.
6. 为了解湖中鱼的多少,某人在湖中打了一网鱼,共m条,做上记号后放入湖中,数日后又打了一网鱼,共n条,其中k条鱼有记号,估计湖中有鱼( )
A、条 B、条
C、m条 D、无法估计
答案:B
解析:解答:∵做记号的鱼已经完全分散开了,是分布均匀的.
∴湖中每个个体被抽到的机会都相等,
∴,
∴x=.
故选B.
分析:依据湖中每个个体被抽到的机会都相等列式解决.
7. 为了了解某地参加计算机水平测试的5000名学生的成绩,从中抽取了200名学生的成绩进行统计分析,在这个问题中,下列说法正确的是( )
A、总体指的是参加计算机水平测试的5000名学生
B、个体指的是5000名学生中的每一个学生
C、样本容量指的是抽取的200名学生
D、样本指的是抽取的200名学生的成绩
答案:D
解析:解答:总体指的是参加计算机水平测试的5000名学生的成绩,所以A错;
个体指的是5000名学生中的每一个学生的成绩,所以B错;
样本容量指的是抽取的200,所以C错;
样本指的是抽取的200名学生的成绩正确,所以D对;
故选D.
分析:本题考查的是确定总体.解此类题需要注意“考查对象实际应是表示事物某一特征的数据,而非考查的事物.”我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考查的对象,考查对象是某地区初中毕业生参加中考的数学成绩,再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
8. 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示,时速在[50,60)的汽车大约有( )
( http: / / www.21cnjy.com )
A、30辆 B、60辆
C、300辆 D、600辆
答案:D
解析:解答:∵有频率分步直方图可以看出
在[50,60)之间的频率是0.03×10=0.3,
∴时速在[50,60)的汽车大约有2000×0.3=600
故选D.
分析:根据频率分步直方图可以看出在[50,60)之间的小长方形的长和宽,做出对应的频率,用频率乘以样本容量得到结果.
9. 为了了解商场某日旅游鞋的销售情况,抽取了部分顾客购鞋的尺寸,将所得的数据整理后,画出频率分布直方图如图.已知中从左至右前3个小组的频率之比为1:2:3,第4小组与第5小组的频率分别为0.175和0.075,第二小组的频数为10,则抽取的顾客人数是( )
A、80 B、60
C、40 D、100
答案:C
解析:解答:由题意得:第4小组与第5小组的频率分别为0.175和0.075,
所以前3组的频率和为0.75.
又因为从左至右前3个小组的频率之比为1:2:3,
所以从左至右第2个小组的频率为:0.25.
因为第二小组的频数为10,
所以抽取的顾客人数是=40人.
故选C.
分析:有第四组与第五组的频率和得到前3组的频率和,又根据前三组的频率之比即可得到第二组的频率,结合第二组的频数可得抽取的顾客人数.
10. 某地一种植物一年生长的高度如下表:
( http: / / www.21cnjy.com )
则该植物一年生长在[30,40)内的频率是( )
A、0.80 B、0.65
C、0.40 D、0.25
答案:C
解析:解答:根据频率分布表可知样本容量是20+30+80+40+30,
在[30,40)这组数据中频数是80,
∴由频率的定义得80÷(20+30+80+40+30)=0.40.
故选C.
分析:根据所给的频率分布表看出这组数据的样本容量和落在所要求的范围的频数,根据样本容量,频数和频率之间的关系得到要求的结果.
11. 总体已经分成A,B,C三层,A,B,C三层个体数之比为2:3:5,现从总体中抽取容量为20的一个样本,已知A层中用简单随机抽样抽取样本时,甲被抽到的概率为,则总体的个体个数为( )
A、40 B、80
C、120 D、160
答案:B
解析:解答:∵现从总体中抽取容量为20的一个样本,
甲被抽到的概率为,
∴在整个抽样过程中每个个体被抽到的概率是
∴总体的个体个数为=80
故选B.
分析:根据现从总体中抽取容量为20的一个样本,个体甲被抽到的概率为,得到在整个抽样过程中每个个体被抽到的概率是,根据频率,频数和样本容量之间的关系得到结果.
12. 如图是某城市100位居民去年的月均用水量 (单位:t)的频率分布直方图,月均用水量在区间[1.5,2.5)的居民大约有( )
A、37位 B、40位
C、47位 D、52位
答案:C
解析:解答:由频率分布直方图月均用水量在区间[1.5,2)的频率为0.45×0.5=0.225.月均用水量在区间[2,2.5)的居民的频率 为0.50×0,5=0.25.
月均用水量在区间[1.5,,2.5)的居民的频数大约为(0.225+0.25)×100=47
故选C.
分析:先根据频率分布直方图求出月均用水量在区间[1.5,2),[2,2.5)的居民的频率.再求出居民的大约数.
二、填空题
13. 对某学校n名学生的体重进行统计,得到频率分布直方图如图所示,则体重在75kg以上的学生人数为64人,则n= .
( http: / / www.21cnjy.com )
答案:400
解析:解答:体重在75kg以上的学生的频率为:0.032×5=0.16
所以体重在75kg以上的同学的人数为:n×0.16=64, n=400
故答案为:400.
分析:由频率分布直方图计算出体重在75kg以上的学生的频率,再利用频率和样本容量的关系计算即可.
14. 某校在学生的一次百米跑测试成绩中抽取50名学生的成绩进行统计,其频率分布直方图如图所示,则成绩小于17秒的学生人数为 .
答案:45
解析:解答:由频率分布直方图知,成绩小于17秒的频率为:
(0.02+0.18+0.36+0.34)×1=0.9.
所以成绩小于17秒的学生人数为0.9×50=45.
故答案为45.
分析:由频率分布直方图得到成绩小于17秒的频率;利用频数等于频率乘以样本容量,求出成绩小于17秒的学生人数.
15. 某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),把其中不低于50 分的分成五段[50,60),[60,70),[70,80),[80,90),[90,100]然后画出如下图的部分频率分布直方图.观察图形的信息,可知数学成绩低于50分的学生有 人;估计这次考试数学学科的及格率(60分及以上为及格)为 ;
( http: / / www.21cnjy.com )
答案:6|75%
解析:解答:由图可知,成绩在[50,60)的频率为0,015×10=0.15,成绩在[60,70)的频率为0.015×10=0.15,
成绩在[70,80)的频率为0.030×10=0.3,成绩在[80,90)的频率为0.025×10=0.25,
成绩在[90,100]的频率为0.005×10=0.05,
∴成绩不低于50 分的频率为0.15+0.15+0.3+0.25+0.05=0.9,成绩不低于60分的频率为0.15+0.3+0.25+0.05=0.75
∴成绩低于50分的频率为为1﹣0.9=0.1
∵共有60名学生,∴成绩低于50分的学生数为60×0.1=6,这次考试数学学科的及格率为75%.
故答案为6;75%
分析:先根据频率分布直方图,求出每段的频率,再计算出成绩低于50分的频率和成绩不低于60分的频率,则成绩低于50分的学生数就是它的频率乘以学生总数,这次考试数学学科的及格率就是成绩不低于60分的频率.
16. 从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:
则成绩在79.5~89.5这一组的频率为 .
( http: / / www.21cnjy.com )答案:0.25
解析:解答:∵每小组的频率=,
由频率的意义可知,
∴成绩在79.5~89.5这一组的频率
=0.025×10=0.25.
故填:0.25.
分析:根据直方图中79.5~89.5这一组的高度及频率的计算公式,可得成绩在79.5~89.5这一组的频率,进而可得答案.
17. 某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的同学为 人.
答案:30
解析:解答:∵这100名同学中学习时间在6~8小时外的频率为
(0.04+0.12+0.14+0.05)×2=0..7
∴这100名同学中学习时间在6~8小时内为1﹣0.7=0.3
∴这100名同学中学习时间在6~8小时内的同学为100×0.3=30
故答案为:30
分析:利用频率分布直方图中,频率等于纵坐标乘以组距,求出在6~8小时外的频率;利用频率和为1,求出在6~8小时内的频率;利用频数等于频率乘以样本容量,求出这100名同学中学习时间在6~8小时内的同学的人数.
18. 某高级中学共有学生3000名,各年级男、女生人数如下表:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.现对各年级用分层抽样的方法在全校抽取300名学生,则应在高三年级抽取 名学生.
( http: / / www.21cnjy.com )
答案:99
解析:解答:∵抽到高二年级女生的概率是0.17,
∴高二年级女生有0.17×3000=510,
∴高三年级共有3000﹣523﹣487﹣490﹣510=990,
∵对各年级用分层抽样的方法在全校抽取300名学生,
∴每个学生被抽到的概率是,
∴应在高三抽取0.1×990=99
故答案为:99
分析:根据要在高二女生中抽取一个人的概率,做出高二女生的人数,用所有的人数减去高一和高二的人数,得到高三共有的人数,根据要抽取的人数和总体数,求出每个个体被抽到的概率,乘以高三的人数,得到结果.
三、解答题
19. 某学校随机抽取部分新生调查其上学 ( http: / / www.21cnjy.com / )路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(1)求直方图中x的值;
答案:解:由(x+0.0125+0.0065+0.003×2)×20=1,
解得x=0.025;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿.
答案:解:上学所需时间不少于40的学生的频率为:(0.0065+0.003×2)×20=0.25,
估计学校1000名新生中有:1000×0.25=250,
答:估计学校1000名新生中有250名学生可以申请住宿.
解析:分析:(1)根据频率分布直方图可以得到组距,而频率分布直方图的纵坐标与组距之积为频率,各组频率之和为1即可得到x的值.(2)根据频率分布直方图求出上学路上所需时间不少于60分钟的学生的频率,频率乘以总人数即可得到可以留宿学生的人数
20. 某校为了解毕业班学业水平考试学生的数 ( http: / / www.21cnjy.com )学考试情况,抽取了该校100名学生的数学成绩,将所有数据整理后,画出了样频率分布直方图(所图所示),若第1组、第9组的频率各为x.
(1) 求x的值,并估计这次学业水平考试数学成绩的平均数;
答案:解:
=0.03
由图可估计样本平均数=0.03×(62.5+102.5)+5×(0.012×67.5+0.012×72.5+0.024×77.5
+0.020×82.5+0.054×87.5+0.036×92.5+0.030×97.5)
=85.
(2)若全校有1500名学生参加了此次考试,估计成绩在[80,100)分内的人数.
答案:解:由图可知样本数据在[80,100)分内的频率为(0.02+0.054+0.036+0.03)×5=0.7,
则可以估计此次考试中成绩在[80,100)内的人数为
1500×0.7=1050(人).
( http: / / www.21cnjy.com )
解析:分析:(1)根据所以频率的和为1,求x的值,用每一组的平均值乘以改组的频率,相加即得所求的这次学业水平考试数学成绩的平均数的估算值,(2)由图可知样本数据在[80,100)分内的频率,用全校的总人数乘以这个频率,即可求得此次考试中成绩在[80,100)分内的人数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 第 12 页 (共 12 页) 版权所有@21世纪教育网
