沪科版(2024)七年级下册数学10.1.2 垂线课件(共29张PPT)
文档属性
| 名称 | 沪科版(2024)七年级下册数学10.1.2 垂线课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第十章 相交线、平行线与平移 10.1
相交线
10.1.2 垂线
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.了解垂线的概念,能用不同方法画垂线.
2.理解并掌握垂线的基本事实,能利用垂线的定义计算角的度数.
学习目标
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
新课导入
思考1:在木条b 转动的过程中,什么量也随之发生改变?
a
b
α
α
α
α
α
b
b
b
b
思考2:∠α=90°的情况有几个?此时木条a,b所在的直线有什么特殊的位置关系?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
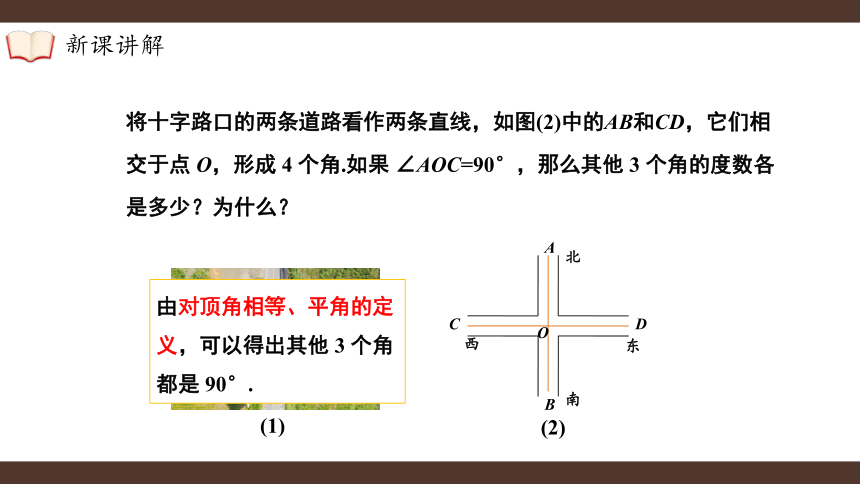
将十字路口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点 O,形成 4 个角.如果 ∠AOC=90°,那么其他 3 个角的度数各是多少?为什么?
(1)
C
A
D
B
南
东
北
西
O
(2)
由对顶角相等、平角的定义,可以得出其他 3 个角都是 90°.
新课讲解
在两条直线 AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直.
A
B
C
D
O
知识点1 垂线的定义
记作:AB⊥CD
读作:AB垂直于CD
其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
反过来,如果AB⊥CD,那么∠AOC是多少度?
新课讲解
垂线的判定及性质
A
B
C
D
O
符号语言:
①判定:因为∠AOD=90°(已知),
所以AB⊥CD(垂直的定义).
②性质:因为 AB⊥CD (已知),
所以∠AOD=90°(垂直的定义).
(∠AOC =∠BOC =∠BOD =90°)
新课讲解
日常生活中两条直线垂直的例子很多,如:
你能再举出生活中一些两条直线互相垂直的例子吗
新课讲解
例1 如图,直线AB与CD相交于点O,且∠AOC=∠BOC.那么直线AB与CD有什么位置关系?为什么?
【选自教材P131练习第1题】
C
D
A
B
O
解:因为∠AOC+∠BOC=180°
(平角的定义),
又∠AOC=∠BOC,
所以∠AOC=∠BOC=90°.
所以AB⊥CD(垂线的定义).
新课讲解
例2 如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:因为∠BOE=∠NOE,
所以∠BON=2∠EON=40°,
所以∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
因为AO⊥BC,
所以∠AOC=90°,
所以∠AOM=∠AOC-∠MOC=90°-40°=50°,
即∠NOC=140°,∠AOM=50°.
新课讲解
知识点2 垂线的画法及基本事实
1.用折纸方法画垂线
使折痕经过已知点P,且使已知直线l两边的部分重合
沿折痕所画的直线就是直线l的垂线
折纸法画垂线
新课讲解
2.用三角板画垂线
落:让三角尺的一条直角边落在已知直线上,使其与已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿已知点所在的直角边画直线,这条直线就是已知直线的垂线.
1
2
3
新课讲解
l
P
1.落
2.移
3.画
1条
(1)经过直线上一点 P 画 l 的垂线,
这样的垂线能画几条?
新课讲解
l
P
1.落
2.移
3.画
1条
(2)经过直线外一点 P 画 l 的垂线,
这样的垂线能画几条?
新课讲解
l
P
点 P 在直线 l 上
l
P
点 P 在直线 l 外
3.用量角器画垂线
根据以上操作,你能得出什么结论?
新课讲解
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
如果不在同一平面内,那么过一点有无数条直线与已知直线垂直
这一点可以在已知直线上,也可以在已知直线外
“有”指存在,“只有”指唯一性
新课讲解
思考1:如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
思考2:如何过一点画一条线段或射线的垂线?
B
A
B
A
是指画它们所在直线的垂线.
新课讲解
例3 如图,在三角形ABC中,D是BC中点,连接AD,请分别画出自点B,C向AD所作的垂线(垂足为点E,F).
【选自教材P132练习第2题】
C
D
A
B
E
F
新课讲解
1.如图,点O在直线 AB 上,OC⊥OD.若∠AOC=120°,则∠BOD 的大小为( )
A.30°
B.40°
C.50°
D.60°
A
课堂练习
2.如图,直线 AB 和 CD 相交于点 O,则下列条件中不能说明 AB⊥CD 的是( )
A.∠AOC=90°
B.∠AOD+∠BOC=180°
C.∠AOC=∠BOD
D.∠AOC=∠BOC
C
课堂练习
3.如图,直线 AB,CD 相交于点O,OF平分∠BOE,∠DOF=25°,∠AOC=40°,OE与 CD 垂直吗?为什么?
解:OE⊥CD.理由如下:
因为∠AOC=40°,
所以∠DOB=∠AOC=40°.
因为∠DOF=25°,
所以∠BOF=∠DOB+∠DOF=65°.
又因为OF平分∠BOE,
所以∠EOF=∠BOF=65°.
所以∠DOE=∠EOF+∠DOF=90°,
所以OE⊥CD.
课堂练习
4.如图,O为直线 AB上一点,过点 O作射线 OC.已知 OD平分∠AOC,OE平分∠BOC,请问 OD与 OE有什么位置关系?并说明理由.
解:OD⊥OE.理由如下:
因为OD平分∠AOC,OE平分∠BOC,
所以∠DOC= ∠AOC,∠COE= ∠BOC,
所以∠DOE=∠DOC+∠COE=
(∠AOC+∠BOC)= ×180°=90°,
所以OD⊥OE.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在两条直线相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直.
其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足.
垂线
基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第十章 相交线、平行线与平移 10.1
相交线
10.1.2 垂线
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.了解垂线的概念,能用不同方法画垂线.
2.理解并掌握垂线的基本事实,能利用垂线的定义计算角的度数.
学习目标
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
新课导入
思考1:在木条b 转动的过程中,什么量也随之发生改变?
a
b
α
α
α
α
α
b
b
b
b
思考2:∠α=90°的情况有几个?此时木条a,b所在的直线有什么特殊的位置关系?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
将十字路口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点 O,形成 4 个角.如果 ∠AOC=90°,那么其他 3 个角的度数各是多少?为什么?
(1)
C
A
D
B
南
东
北
西
O
(2)
由对顶角相等、平角的定义,可以得出其他 3 个角都是 90°.
新课讲解
在两条直线 AB和CD相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直.
A
B
C
D
O
知识点1 垂线的定义
记作:AB⊥CD
读作:AB垂直于CD
其中一条直线叫作另一条直线的垂线,它们的交点O叫作垂足.
反过来,如果AB⊥CD,那么∠AOC是多少度?
新课讲解
垂线的判定及性质
A
B
C
D
O
符号语言:
①判定:因为∠AOD=90°(已知),
所以AB⊥CD(垂直的定义).
②性质:因为 AB⊥CD (已知),
所以∠AOD=90°(垂直的定义).
(∠AOC =∠BOC =∠BOD =90°)
新课讲解
日常生活中两条直线垂直的例子很多,如:
你能再举出生活中一些两条直线互相垂直的例子吗
新课讲解
例1 如图,直线AB与CD相交于点O,且∠AOC=∠BOC.那么直线AB与CD有什么位置关系?为什么?
【选自教材P131练习第1题】
C
D
A
B
O
解:因为∠AOC+∠BOC=180°
(平角的定义),
又∠AOC=∠BOC,
所以∠AOC=∠BOC=90°.
所以AB⊥CD(垂线的定义).
新课讲解
例2 如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数.
解:因为∠BOE=∠NOE,
所以∠BON=2∠EON=40°,
所以∠NOC=180°-∠BON
=180°-40°=140°,
∠MOC=∠BON=40°.
因为AO⊥BC,
所以∠AOC=90°,
所以∠AOM=∠AOC-∠MOC=90°-40°=50°,
即∠NOC=140°,∠AOM=50°.
新课讲解
知识点2 垂线的画法及基本事实
1.用折纸方法画垂线
使折痕经过已知点P,且使已知直线l两边的部分重合
沿折痕所画的直线就是直线l的垂线
折纸法画垂线
新课讲解
2.用三角板画垂线
落:让三角尺的一条直角边落在已知直线上,使其与已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿已知点所在的直角边画直线,这条直线就是已知直线的垂线.
1
2
3
新课讲解
l
P
1.落
2.移
3.画
1条
(1)经过直线上一点 P 画 l 的垂线,
这样的垂线能画几条?
新课讲解
l
P
1.落
2.移
3.画
1条
(2)经过直线外一点 P 画 l 的垂线,
这样的垂线能画几条?
新课讲解
l
P
点 P 在直线 l 上
l
P
点 P 在直线 l 外
3.用量角器画垂线
根据以上操作,你能得出什么结论?
新课讲解
垂线的基本事实
同一平面内,过一点有且只有一条直线与已知直线垂直.
如果不在同一平面内,那么过一点有无数条直线与已知直线垂直
这一点可以在已知直线上,也可以在已知直线外
“有”指存在,“只有”指唯一性
新课讲解
思考1:如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、线段与射线垂直、线段与直线垂直、射线与直线垂直,都是指它们所在的直线垂直.
思考2:如何过一点画一条线段或射线的垂线?
B
A
B
A
是指画它们所在直线的垂线.
新课讲解
例3 如图,在三角形ABC中,D是BC中点,连接AD,请分别画出自点B,C向AD所作的垂线(垂足为点E,F).
【选自教材P132练习第2题】
C
D
A
B
E
F
新课讲解
1.如图,点O在直线 AB 上,OC⊥OD.若∠AOC=120°,则∠BOD 的大小为( )
A.30°
B.40°
C.50°
D.60°
A
课堂练习
2.如图,直线 AB 和 CD 相交于点 O,则下列条件中不能说明 AB⊥CD 的是( )
A.∠AOC=90°
B.∠AOD+∠BOC=180°
C.∠AOC=∠BOD
D.∠AOC=∠BOC
C
课堂练习
3.如图,直线 AB,CD 相交于点O,OF平分∠BOE,∠DOF=25°,∠AOC=40°,OE与 CD 垂直吗?为什么?
解:OE⊥CD.理由如下:
因为∠AOC=40°,
所以∠DOB=∠AOC=40°.
因为∠DOF=25°,
所以∠BOF=∠DOB+∠DOF=65°.
又因为OF平分∠BOE,
所以∠EOF=∠BOF=65°.
所以∠DOE=∠EOF+∠DOF=90°,
所以OE⊥CD.
课堂练习
4.如图,O为直线 AB上一点,过点 O作射线 OC.已知 OD平分∠AOC,OE平分∠BOC,请问 OD与 OE有什么位置关系?并说明理由.
解:OD⊥OE.理由如下:
因为OD平分∠AOC,OE平分∠BOC,
所以∠DOC= ∠AOC,∠COE= ∠BOC,
所以∠DOE=∠DOC+∠COE=
(∠AOC+∠BOC)= ×180°=90°,
所以OD⊥OE.
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在两条直线相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直.
其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足.
垂线
基本事实:同一平面内,过一点有且只有一条直线与已知直线垂直.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.课后习题中选取;
2.完成练习册本课时的习题.
课后作业
