第十八章平行四边形单元测试(A卷)(含答案)
文档属性
| 名称 | 第十八章平行四边形单元测试(A卷)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 592.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 15:49:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形单元测试(A卷)人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
2.如图,在△ABC中,∠ACB=90°,AB=2cm,点D为AB的中点,则CD=( )
A.1cm B.2cm C.3cm D.4cm
3.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为( )
A. B. C.3 D.5
5.如图,在平行四边形ABCD中,AB=3,OA=2,BD=8,则△ABO的周长为( )
A.8 B.9 C.10 D.13
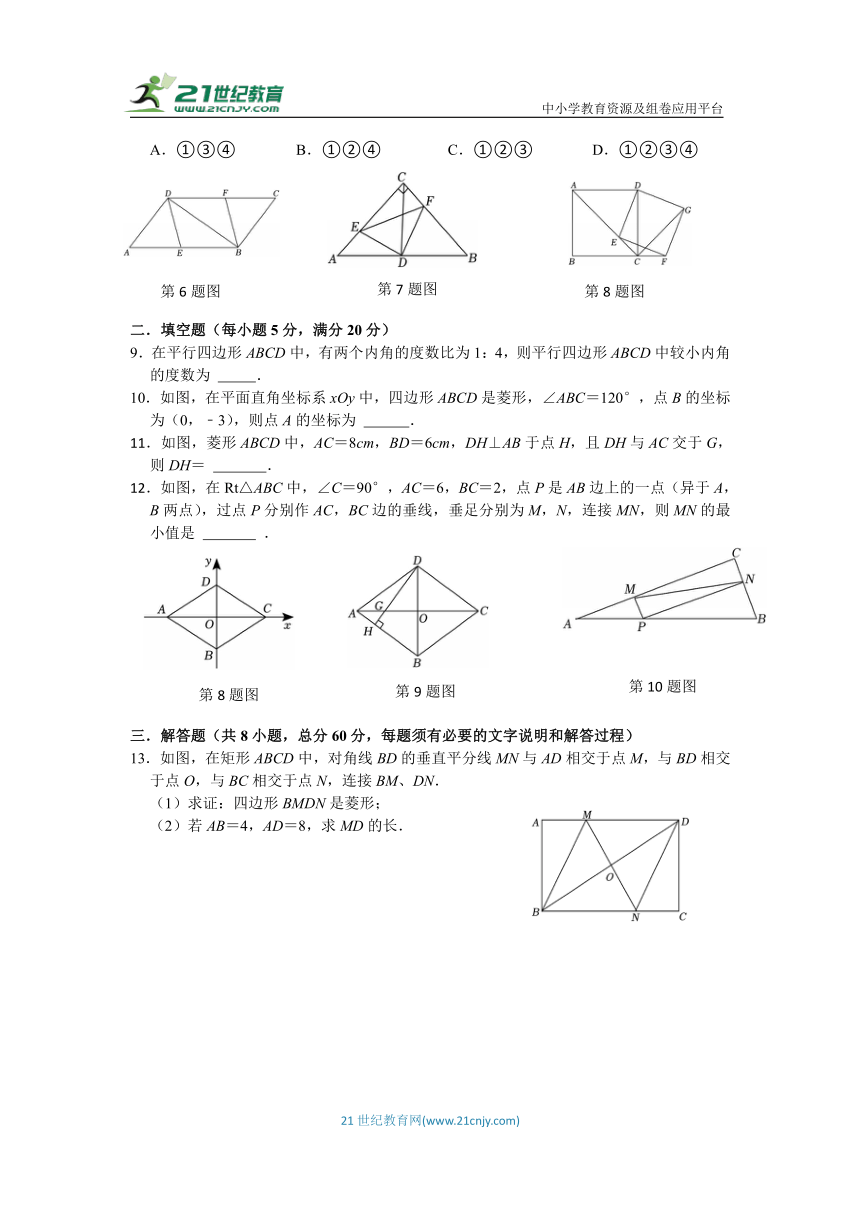
6.如图,在 ABCD中,E、F分别为边AB、CD的中点,BD是对角线.下列说法错误的是( )
A.当AB=2AD时,四边形DEBF是菱形
B.当∠ADB=90°时,四边形DEBF是菱形
C.当AD=BD时,四边形DEBF是矩形
D.当DE平分∠ADB时,四边形DEBF是矩形
7.如图,CD是Rt△ABC斜边上的中线,E,F分别在直角边AC,BC上,连接DE,DF,使DE⊥DF.若AE=1,BF=2,则EF的长为( )
A.3 B. C.5 D.
8.如图,已知四边形ABCD为正方形,,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC的延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论:①矩形DEFG是正方形;②CE=CF;③CG平分∠DCF;④CG=AE.其中结论正确的序号有( )
A.①③④ B.①②④ C.①②③ D.①②③④
二.填空题(每小题5分,满分20分)
9.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
10.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣3),则点A的坐标为 .
11.如图,菱形ABCD中,AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH= .
12.如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
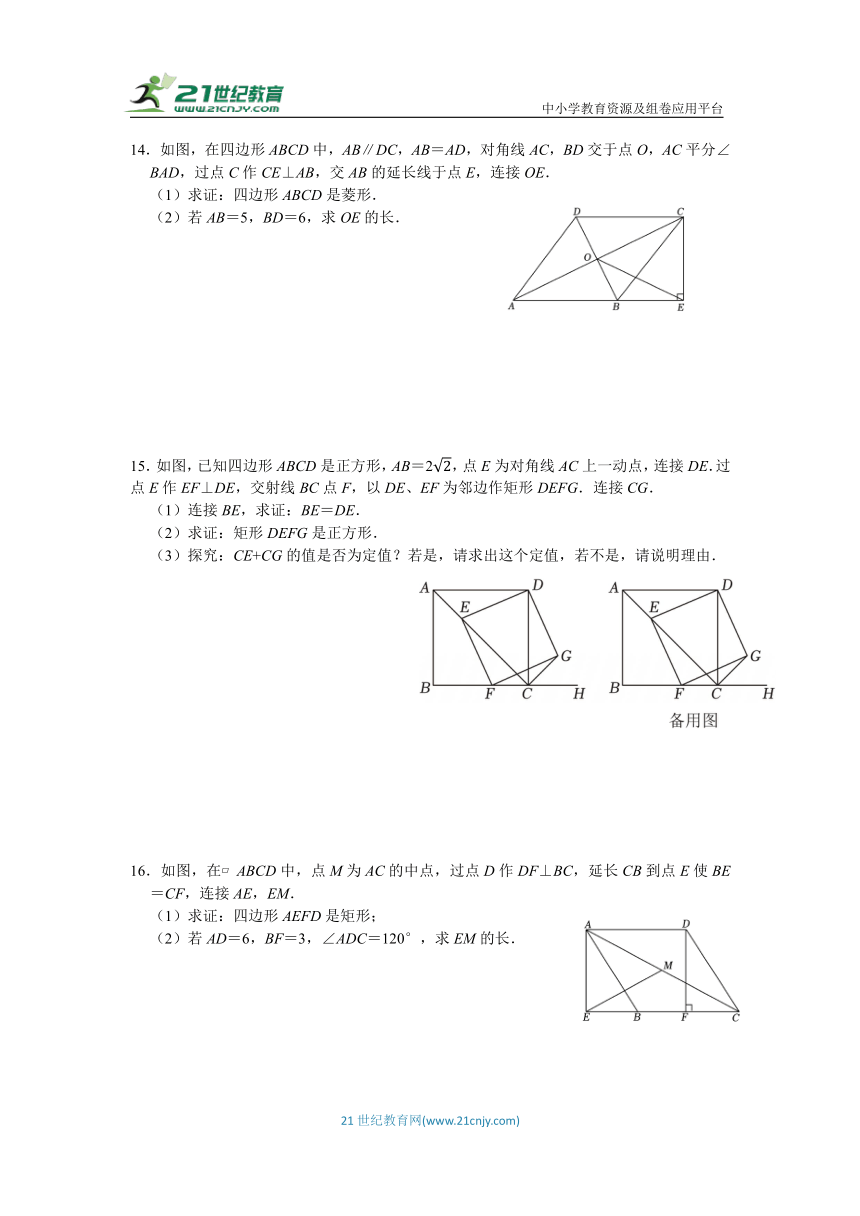
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
15.如图,已知四边形ABCD是正方形,AB=2,点E为对角线AC上一动点,连接DE.过点E作EF⊥DE,交射线BC点F,以DE、EF为邻边作矩形DEFG.连接CG.
(1)连接BE,求证:BE=DE.
(2)求证:矩形DEFG是正方形.
(3)探究:CE+CG的值是否为定值?若是,请求出这个定值,若不是,请说明理由.
16.如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
17.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
18.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
参考答案
一、选择题
1—8:BADBBDDA
二、填空题
9.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
10.【解答】解:四边形ABCD是菱形,∠ABC=120°,
∴,
∴∠BAO=30°,
∴AB=2OB,
∵点B的坐标为(0,﹣3),
∴OB=3,
∴AB=2OB=6,
∴,
∴点A的坐标为,
故答案为:.
11.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC8=4(cm),OB=ODBD6=3(cm),
在Rt△AOB中,由勾股定理得:AB5(cm),
∵S菱形ABCDAC BD=AB DH,
∴DH(cm),
故答案为:cm.
12.【解答】解:如图,连接PC.
在△ABC中,∠C=90°,AC=6,BC=2,
∴AB2,
∵PM⊥AC,PN⊥BC,
∴∠PMC=∠PNC=∠C=90°,
∴四边形PMCN是矩形,
∴MN=PC,
当PC⊥AB时,PC的值最小,
此时PC的最小值,
∴MN的最小值为,
故答案为:.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:连接BE,
∵四边形ABCD是正方形,
∴BA=DA,∠BAE=∠DAE,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(3)解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CEAB24,
∴CE+CG=4 是定值.
16.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
17.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
18.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
21世纪教育网(www.21cnjy.com)
第十八章平行四边形单元测试(A卷)人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD
2.如图,在△ABC中,∠ACB=90°,AB=2cm,点D为AB的中点,则CD=( )
A.1cm B.2cm C.3cm D.4cm
3.下列说法中,正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
4.如图,在菱形ABCD中,对角线AC、BD相交于点O,H为BC中点,AC=6,BD=8.则线段OH的长为( )
A. B. C.3 D.5
5.如图,在平行四边形ABCD中,AB=3,OA=2,BD=8,则△ABO的周长为( )
A.8 B.9 C.10 D.13
6.如图,在 ABCD中,E、F分别为边AB、CD的中点,BD是对角线.下列说法错误的是( )
A.当AB=2AD时,四边形DEBF是菱形
B.当∠ADB=90°时,四边形DEBF是菱形
C.当AD=BD时,四边形DEBF是矩形
D.当DE平分∠ADB时,四边形DEBF是矩形
7.如图,CD是Rt△ABC斜边上的中线,E,F分别在直角边AC,BC上,连接DE,DF,使DE⊥DF.若AE=1,BF=2,则EF的长为( )
A.3 B. C.5 D.
8.如图,已知四边形ABCD为正方形,,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC的延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.下列结论:①矩形DEFG是正方形;②CE=CF;③CG平分∠DCF;④CG=AE.其中结论正确的序号有( )
A.①③④ B.①②④ C.①②③ D.①②③④
二.填空题(每小题5分,满分20分)
9.在平行四边形ABCD中,有两个内角的度数比为1:4,则平行四边形ABCD中较小内角的度数为 .
10.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,∠ABC=120°,点B的坐标为(0,﹣3),则点A的坐标为 .
11.如图,菱形ABCD中,AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则DH= .
12.如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
14.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB,交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形.
(2)若AB=5,BD=6,求OE的长.
15.如图,已知四边形ABCD是正方形,AB=2,点E为对角线AC上一动点,连接DE.过点E作EF⊥DE,交射线BC点F,以DE、EF为邻边作矩形DEFG.连接CG.
(1)连接BE,求证:BE=DE.
(2)求证:矩形DEFG是正方形.
(3)探究:CE+CG的值是否为定值?若是,请求出这个定值,若不是,请说明理由.
16.如图,在 ABCD中,点M为AC的中点,过点D作DF⊥BC,延长CB到点E使BE=CF,连接AE,EM.
(1)求证:四边形AEFD是矩形;
(2)若AD=6,BF=3,∠ADC=120°,求EM的长.
17.如图1,在菱形ABCD中,E是边BC上的点,△AEF是等腰三角形,AE=EF,∠AEF=∠ABC=α(α≥90°).
(1)如图2,当α=90°时,连接BD交AF于点P,
①直接写出∠DCF的度数;
②求证:.
(2)如图1,当∠DCF=135°时,若,求的值.
18.将一个矩形纸片OABC放置在平面直角坐标系xOy内,边OA、OC分别在x轴、y轴上,B点坐标是(a,b)且a、b满足(a+b﹣10)2=0,点P是线段B上的动点,将△OCP沿OP翻折得到△OC′P.
(1)求点A和C的坐标;
(2)如图①,当点C′落在线段AP上时,求点P的坐标;
(3)如图②,当点P为线段BC中点时,求线段BC′的长度.
参考答案
一、选择题
1—8:BADBBDDA
二、填空题
9.【解答】解:如图:
∵四边形ABCD为平行四边形,有两个内角的度数比为1:4,
∴AD∥BC,∠A=4∠B,
∴∠A+∠B=180°,
∴4∠B+∠B=180°,
∴∠B=36°,
∴∠A=144°,
∴平行四边形ABCD中较小内角的度数为36°,
故答案为:36°.
10.【解答】解:四边形ABCD是菱形,∠ABC=120°,
∴,
∴∠BAO=30°,
∴AB=2OB,
∵点B的坐标为(0,﹣3),
∴OB=3,
∴AB=2OB=6,
∴,
∴点A的坐标为,
故答案为:.
11.【解答】解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OCAC8=4(cm),OB=ODBD6=3(cm),
在Rt△AOB中,由勾股定理得:AB5(cm),
∵S菱形ABCDAC BD=AB DH,
∴DH(cm),
故答案为:cm.
12.【解答】解:如图,连接PC.
在△ABC中,∠C=90°,AC=6,BC=2,
∴AB2,
∵PM⊥AC,PN⊥BC,
∴∠PMC=∠PNC=∠C=90°,
∴四边形PMCN是矩形,
∴MN=PC,
当PC⊥AB时,PC的值最小,
此时PC的最小值,
∴MN的最小值为,
故答案为:.
三、解答题
13.【解答】解:(1)∵四边形ABCD是矩形
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中
∴△DMO≌△BNO(ASA),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形;
(2)∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8﹣x)2+42,
解得:x=5,
答:MD长为5.
14.【解答】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,对角线AC,BD交于点O,
∴AC⊥BD,OA=OC=,OB=OD=,
∴OB==3,
在Rt△AOB中,∠AOB=90°,
∴OA=,
∵CE⊥AB,
∴∠AEC=90°,
在Rt△AEC中,∠AEC=90°,O为AC中点,
∴=4.
15.【解答】(1)证明:连接BE,
∵四边形ABCD是正方形,
∴BA=DA,∠BAE=∠DAE,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(3)解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CEAB24,
∴CE+CG=4 是定值.
16.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴AD∥EF,
∵BE=CF,
∴BE+BF=CF+BF,即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
又∵DF⊥BC,
∴∠DFE=90°,
∴四边形AEFD是矩形.
(2)解:由(1)可知,∠DFE=∠DFC=90°,AD=EF=BC,
∵AD=6,BF=3,
∴EB=CF=3,EC=9,
∵四边形ABCD是平行四边形,∠ADC=120°,
∴∠DCF=60°,∠CDF=30°,
∴DC=2CF=6,
在Rt△DFC中,由勾股定理得:DF2+CF2=DC2,
∴,
∵四边形AEFD是矩形,
∴,∠AEC=90°,
在Rt△ACE中,由勾股定理得:AE2+EC2=AC2,
∴,
∵M是AC的中点,∠AEC=90°,
∴.
17.【解答】解:(1)①∠DCF的度数是45°,
理由:如图2,作FN⊥CD于点N,FM⊥BC交BC的延长线于点M,则∠M=90°,
∵四边形ABCD是菱形,∠AEF=∠ABC=α=90°,
∴四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCD=90°,
∴∠ABE=∠M,∠BAE=∠MEF=90°﹣∠AEB,∠MCN=90°,
在△ABE和△EMF中,
,
∴△ABE≌△EMF(AAS),
∴AB=EM=BC,BE=MF,
∵BE=BC﹣CE=EM﹣CE=CM,
∴CM=MF,
∴∠MCF=∠MFC=45°,
∴∠DCF=90°﹣∠MCF=45°,
∴∠DCF的度数是45°.
②证明:如图2,连接AC交BD于点Q,连接CP,则AQ=CQ,DQ=BQ,
∵BD垂直平分AC,
∴AP=CP,
∴∠PCA=∠PAC,
∵AD=CD,∠ADC=90°,
∴∠DCA=∠DAC=45°,
∴∠ACF=∠DCA+∠DCF=90°,
∴∠PCF=90°﹣∠PCA=90°﹣∠PAC=∠PFC,
∴FP=CP,
∴AP=FP,
∴CF=2QP,
∴CF+2DP=2QP+2DP=2DQ=BD,
∵BC=CD,∠BCD=90°,
∴BDBC,
∴CF+2DPBC.
(2)如图1,作FL⊥BC交BC的延长线于点L,在CL上取一点H,使CH=BE,连接FH,
∵四边形ABCD是菱形,∠AEF=∠ABC=α,
∴AB=BC=BE+CE=CH+CE=EH,∠BAE=∠HEF=180°﹣α﹣∠AEB,
在△ABE和△EHF中,
,
∴△ABE≌△EHF(SAS),
∴BE=HF,∠B=∠EHF,
∴CH=HF,
∴∠HCF=∠HFC,
∴∠FHL=∠HCF+∠HFC=2∠HCF,
∵AB∥CD,∠DCF=135°,
∴∠B=∠DCH,
∴∠EHF=∠DCH=135°+∠HCF,
∴135°+∠HCF+2∠HCF=180°,
∴∠HCF=15°,
∴∠FHL=30°,
设FL=m,
∵∠L=90°,
∴CH=HF=2FL=2m,
∴HLm,
∴CF2=(2mm)2+m2=(8+4)m2,
∵,
∴ECCH2m=3m,
∴CD=BC=EH=3m+2m=5m,
∴CD2=(5m)2=25m2,
∴,
∴的值为.
18.解:(1)∵(a+b﹣10)2=0,
∴.
解得:,
∴B(6,4),
又∵四边形OABC为矩形,
∴A(6,0),C(0,4);
(2)由(1)可知:AO=BC=6,CO=BA=4,
∵AO∥BC,
∴∠CPO=∠AOP,
由折叠易知:∠CPO=∠C'PO,
∴∠AOP=∠C'PO,
∴AO=AP=6,
在Rt△ABP中,PB.
∴CP=BC﹣PB=6﹣2,
∴点P坐标为:(6﹣2,4);
(3)连接CC',交PO于点D,如图所示:
在Rt△PCO中,OC=4,PC3,
∴OP,
由折叠易知:OP垂直平分线段CC',即D为CC'的中点,
∴S△PCO,
∴CD,
在Rt△PDC中,PD,
又∵D为CC'的中点,P为BC中点,
∴PD为△CC'B的中位线,
∴BC'=2PD=2.
21世纪教育网(www.21cnjy.com)
