第十八章平行四边形单元测试(含答案)
文档属性
| 名称 | 第十八章平行四边形单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 721.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 16:00:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十八章平行四边形单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
5.下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等且互相平分的四边形是菱形
C.对角线垂直且互相平分的四边形是矩形
D.对角线垂直、相等且互相平分的四边形是正方形
6.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
7.如图,在平行四边形ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED是( )
A.2 B.3 C.4 D.5
8.如图,在菱形ABCD中,AC、BD交于O点,AC=8,BD=6,点P为线段AC上的一个动点,过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
9.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,且AB=2,∠AOB=60°,点E为BD上一点,OE=1.连接AE,则AE的长为 .
12.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
14.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
15.如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,CD=AE.
(1)求证:点D在线段CE的垂直平分线上.
(2)①当点D是BC的中点时,求∠B;
②当CD=5,BD=6,求CE.
16.如图,平行四边形ABCD的对角线AC,BD相交于点O,AC平分∠BAD,DP∥AC,CP∥BD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,求OP的长.
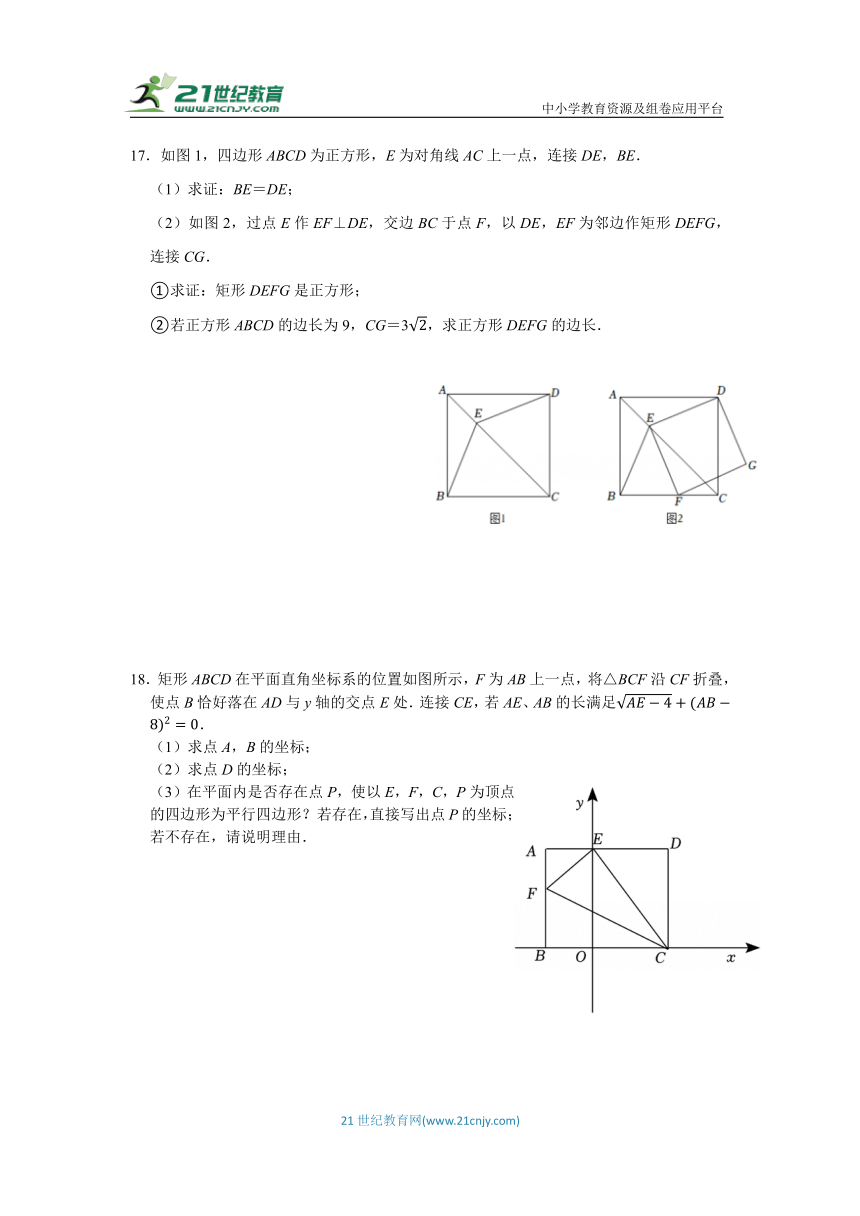
17.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
18.矩形ABCD在平面直角坐标系的位置如图所示,F为AB上一点,将△BCF沿CF折叠,使点B恰好落在AD与y轴的交点E处.连接CE,若AE、AB的长满足.
(1)求点A,B的坐标;
(2)求点D的坐标;
(3)在平面内是否存在点P,使以E,F,C,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1—8:BCCCDDBC
二、填空题
9.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
10.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
11.【解答】解:当点E在OB上或在OD上时,如图,
∵四边形ABCD是矩形,
∴OA=OBAC,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,
①当点E在OB上时,OE=1,
∴BE=1,
∴E是OB的中点,
∴AE⊥OB,
∴OA=2,
∴AE;
②当点E在OD上时为E′,
∴EE′=2,
∴AE′.
则AE的长为:或.
故答案为:或.
12.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
14.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
15.【解答】(1)证明:连接DE,过点E作EH⊥BD于点H,如图所示:
在△ABC中,AD是BC边上的高,
∴△ABD是直角三角形,
∵CE是AB边上的中线,
∴ED是Rt△ABD斜边AB上的中线,
∴ED=AE=BEAB,
∵CD=AE,
∴ED=CD,
∴点D在线段CE的垂直平分线上;
(2)①解:∵点D是BC的中点,
∴BD=CD,
又∵DE=BE=CD,
∴BD=DE=BE,
∴△BDE是等边三角形,
∴∠B=60°;
②解:∵CD=5,BD=6,
由(1)可知:ED=BE=CD=5,
∴△EBD是等腰三角形,
又∵EH⊥BD,
∴BH=DHBD=3,
在Rt△EHD中,由勾股定理得:EH4,
在Rt△EHC中,CH=DH+CD=3+5=8,
由勾股定理得:CE.
16.【解答】(1)证明:∵AC平分∠BAD,
∴∠DAC=∠BAC
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴平行四边形ABCD是菱形;
(2)解:由题意可得:
∴,,AC⊥BD,
∴∠COD=90°,
∵DP∥AC,CP∥BD,∠COD=90°,
∴四边形OCPD是矩形,
∴OP=CD=5.
17.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
18.【解答】解:(1)∵.
又∵0,(AB﹣8)2≥0,
∴AE=4,AB=8,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,AD∥BC,
∴AB⊥BC,
∴A(﹣4,8),B(﹣4,0);
(2)由翻折变换的性质可知CB=CE,
设CB=AD=CE=m,则DE=m﹣4,
∵∠D=90°,
∴CE2=DE2+CD2,
∴m2=(m﹣4)2+82,
∴m=10,
∴AD=BC=10,
∴DE=AD﹣AE=10﹣4=6,
∴D(6,8);
(3)由翻折变换的性质可知FE=FB,
设FE=FB=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴EF2=AF2+AE2,
∴x2=(8﹣x)2+42,
∴x=5,
∴FE=FB=5,
∴F(﹣4,5),
∵E(0,8),C(6,0),
当EF是平行四边形的边时.P(2,﹣3),P′(10,3),
当EF是平行四边形的对角线时,P″(﹣10,13).
综上所述,满足条件的点P的坐标为(2,﹣3)或(10,3)或(﹣10,13).
21世纪教育网(www.21cnjy.com)
第十八章平行四边形单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是( )
A.各角都相等 B.各边都相等
C.有两条对称轴 D.对角线相等
3.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
4.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
5.下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等且互相平分的四边形是菱形
C.对角线垂直且互相平分的四边形是矩形
D.对角线垂直、相等且互相平分的四边形是正方形
6.如图,在Rt△ABC中,∠B=90°,BC=12,AB=5,则斜边上的中线BO长是( )
A.2.5 B.4 C.6 D.6.5
7.如图,在平行四边形ABCD中,AB=4,BC=7,∠ABC的平分线交AD于点E,则ED是( )
A.2 B.3 C.4 D.5
8.如图,在菱形ABCD中,AC、BD交于O点,AC=8,BD=6,点P为线段AC上的一个动点,过点P分别作PM⊥AD于点M,作PN⊥DC于点N,则PM+PN的值为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
9.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,且AB=2,∠AOB=60°,点E为BD上一点,OE=1.连接AE,则AE的长为 .
12.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在平行四边形ABCD中,AC与BD相交于点O,延长CD至点E,使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)若AC平分∠BAE,AC=8,AE=6,求△ACE的面积.
14.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
15.如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,CD=AE.
(1)求证:点D在线段CE的垂直平分线上.
(2)①当点D是BC的中点时,求∠B;
②当CD=5,BD=6,求CE.
16.如图,平行四边形ABCD的对角线AC,BD相交于点O,AC平分∠BAD,DP∥AC,CP∥BD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,求OP的长.
17.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
18.矩形ABCD在平面直角坐标系的位置如图所示,F为AB上一点,将△BCF沿CF折叠,使点B恰好落在AD与y轴的交点E处.连接CE,若AE、AB的长满足.
(1)求点A,B的坐标;
(2)求点D的坐标;
(3)在平面内是否存在点P,使以E,F,C,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题
1—8:BCCCDDBC
二、填空题
9.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
10.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
11.【解答】解:当点E在OB上或在OD上时,如图,
∵四边形ABCD是矩形,
∴OA=OBAC,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,
①当点E在OB上时,OE=1,
∴BE=1,
∴E是OB的中点,
∴AE⊥OB,
∴OA=2,
∴AE;
②当点E在OD上时为E′,
∴EE′=2,
∴AE′.
则AE的长为:或.
故答案为:或.
12.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长CD至点E,使CD=DE,
∴AB∥DE,AB=DE,
∴四边形ABDE是平行四边形.
(2)解:连接OE,
∵ ABCD的对角线AC与BD相交于点O,AC=8,
∴OA=OCAC=4,
∵AC平分∠BAE,
∴∠BAC=∠EAC,
∵AB∥CD,
∴∠BAC=∠ECA,
∴∠EAC=∠ECA,
∴AE=CE=6,
∴OE⊥AC,
∴∠AOE=90°,
∴OE2,
∴S△ACEAC OE8×28,
∴△ACE的面积是8.
14.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
15.【解答】(1)证明:连接DE,过点E作EH⊥BD于点H,如图所示:
在△ABC中,AD是BC边上的高,
∴△ABD是直角三角形,
∵CE是AB边上的中线,
∴ED是Rt△ABD斜边AB上的中线,
∴ED=AE=BEAB,
∵CD=AE,
∴ED=CD,
∴点D在线段CE的垂直平分线上;
(2)①解:∵点D是BC的中点,
∴BD=CD,
又∵DE=BE=CD,
∴BD=DE=BE,
∴△BDE是等边三角形,
∴∠B=60°;
②解:∵CD=5,BD=6,
由(1)可知:ED=BE=CD=5,
∴△EBD是等腰三角形,
又∵EH⊥BD,
∴BH=DHBD=3,
在Rt△EHD中,由勾股定理得:EH4,
在Rt△EHC中,CH=DH+CD=3+5=8,
由勾股定理得:CE.
16.【解答】(1)证明:∵AC平分∠BAD,
∴∠DAC=∠BAC
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠BAC=∠ACB,
∴AB=BC,
∴平行四边形ABCD是菱形;
(2)解:由题意可得:
∴,,AC⊥BD,
∴∠COD=90°,
∵DP∥AC,CP∥BD,∠COD=90°,
∴四边形OCPD是矩形,
∴OP=CD=5.
17.【解答】(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=ACAB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG3,
∴DEEG=3.
∴正方形DEFG的边长为3.
18.【解答】解:(1)∵.
又∵0,(AB﹣8)2≥0,
∴AE=4,AB=8,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,AD∥BC,
∴AB⊥BC,
∴A(﹣4,8),B(﹣4,0);
(2)由翻折变换的性质可知CB=CE,
设CB=AD=CE=m,则DE=m﹣4,
∵∠D=90°,
∴CE2=DE2+CD2,
∴m2=(m﹣4)2+82,
∴m=10,
∴AD=BC=10,
∴DE=AD﹣AE=10﹣4=6,
∴D(6,8);
(3)由翻折变换的性质可知FE=FB,
设FE=FB=x,
∵四边形ABCD是矩形,
∴∠A=90°,
∴EF2=AF2+AE2,
∴x2=(8﹣x)2+42,
∴x=5,
∴FE=FB=5,
∴F(﹣4,5),
∵E(0,8),C(6,0),
当EF是平行四边形的边时.P(2,﹣3),P′(10,3),
当EF是平行四边形的对角线时,P″(﹣10,13).
综上所述,满足条件的点P的坐标为(2,﹣3)或(10,3)或(﹣10,13).
21世纪教育网(www.21cnjy.com)
