2024-2025学年上海育才中学高一下学期期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海育才中学高一下学期期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 903.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 16:24:46 | ||
图片预览




文档简介
育才中学2024-2025学年第二学期高一年级数学期中
2025.4
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的最小正周期为________.
2.化简:________.
3.已知角的终边经过点,则________.
4.水滴是刘慈欣的科幻小说《三体Ⅱ》中提到的由三体文明使用强互作用力(SIM)材料所制成的宇宙探测器,因为其外形与水滴相似,所以被人类称为水滴.如图所示,水滴是由线段,和圆的优弧围成,其中,恰好与圆弧相切.若圆弧所在圆的半径为2,点到圆弧所在圆圆心的距离为4,则该封闭图形的面积为________.
5.已知,,则在方向上的数量投影是________.
6.已知函数有最小值,则实数的取值范围为________.
7.如图,某侦察飞机沿水平直线匀速飞行.在处观测地面目标,测得俯角.飞行后到达处,此时观测地面目标,测得俯角.又飞行一段时间后到达处,此时观测地面目标,测得俯角的余弦值为,则该侦察飞机由至的飞行时间为________.
8.设为平行四边形的对角线、的交点,为平行四边形所在平面内的一个动点,若,则________.
9.在中,角,,的对边分别为,,,且,若,则对任意,的最小值为________.
10.设,当实数变化时,在区间中至少有个零点,至多有个零点,则________.
11.折扇又名“撒扇”、“纸扇”,是一种用竹木或象牙做扇骨,韧纸或绫绢做扇面的能折叠的扇子,如图1.其展开几何图是如图2的扇形,其中,,
,点在上(包含端点),则的取值范围是________.
12.函数,,,,对任意实数,,当时,都有成立,将函数的图像向左平移个单位得到函数,若函数的最大值为10,则的最小值为________.
二、选择题(本大题共4题,每题5分,共20分)
13.“为锐角”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
14.已知平面向量,不共线,,,,则( )
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
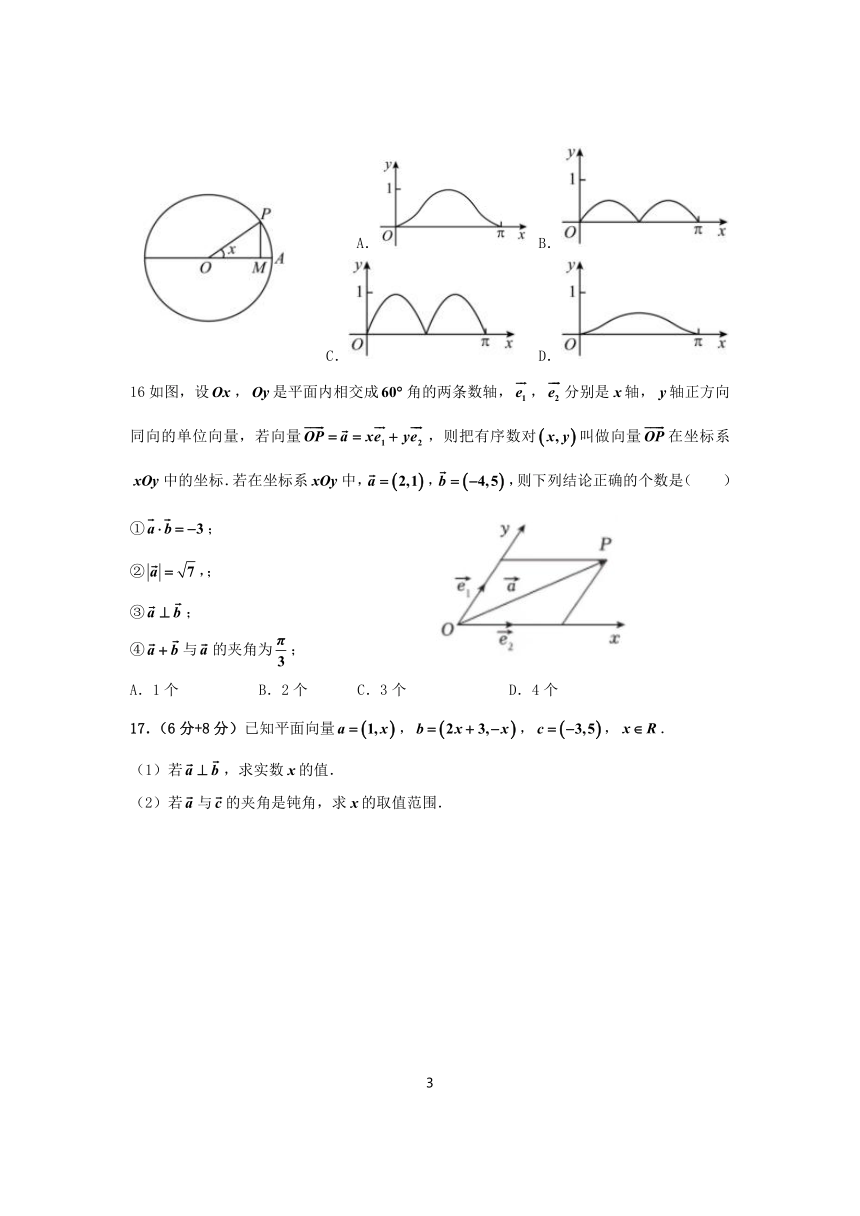
15.如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则在上的图像大致为( )
A. B.
C. D.
16如图,设,是平面内相交成角的两条数轴,,分别是轴,轴正方向同向的单位向量,若向量,则把有序数对叫做向量在坐标系中的坐标.若在坐标系中,,,则下列结论正确的个数是( )
①;
②,;
③;
④与的夹角为;
A.1个 B.2个 C.3个 D.4个
17.(6分+8分)已知平面向量,,,.
(1)若,求实数的值.
(2)若与的夹角是钝角,求的取值范围.
18.(6分+8分)已知二次函数满足,函数满足,且不等式的解集为.
(1)求的解析式;
(2)若关于的不等式对任意的恒成立,求实数的取值范围.
19.(4分+4分+6分)游客坐在摩天轮的座舱里慢慢的往上转,可以从高处俯瞰四周景色.如图1,该摩天轮最高点距离地面高度为90米,转盘直径为88米,设置有56个座舱,摩天轮上的座舱运动可以近似的看作是质点在圆周上做匀速圆周运动,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要18分钟.如图2,设座舱距离地面最近的位置为点,
(1)游客小明坐上摩天轮的座舱,开始转动分钟后距离地面的高度为米,求在转动一周的过程中,关于的函数解析式,;
(2)坐上摩天轮转动一圈,当距离地面68米及以上高度时游客就能俯瞰全景,大有“一览众山小”之感.小明能有多长时间感受这个过程?
(3)小明在摩天轮上发现朋友小华刚要入舱乘坐摩天轮,而且小华的座舱和自己的座舱之间还有13个座舱,求从小明坐上摩天轮座舱开始计时,到小明运行一周结束计时,问在什么时刻两人距离地面的高度差最大,最大值是多少?
20.(5分+5分+6分)已知,,函数.
(1)求函数的解析式及其图象的对称中心;
(2)若,且,求的值;
(3)在锐角中,角,,分别为,,三边所对的角,若,,求周长的取值范围.
21.(4分+6分+8分)“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:
已知的内角,,所对的边分别为,,,
(1)若,求;
(2)在(1)的条件下,若,设点为的费马点,求;
(3)若,设点为的费马点,,求实数的最小值.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
11.折扇又名“撒扇”、“纸扇”,是一种用竹木或象牙做扇骨,韧纸或绫绢做扇面的能折叠的扇子,如图1.其展开几何图是如图2的扇形,其中,,
,点在上(包含端点),则的取值范围是________.
【答案】
【解析】设是弧的中点,连接,
因为,所以三角形和三角形是等边三角形,
所以四边形是菱形,则,且,
因为点在上(包含端点),所以,
因为,所以
因为,所以
所以,所以的取值范围是.故答案为:.
二、选择题
13.A 14.D 15.B 16.C
15.如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则在上的图像大致为( )
A.B.
C. D.
【答案】B
【解析】如图:过作于,
则由题意可得:,
在Rt中,,
所以
所以,其图象即为选项.故选:B.
16如图,设,是平面内相交成角的两条数轴,,分别是轴,轴正方向同向的单位向量,若向量,则把有序数对叫做向量在坐标系中的坐标.若在坐标系中,,,则下列结论正确的个数是( )
①;
②,;
③;
④与的夹角为;
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】因为,,且
所以,选项错误;
,所以,选项正确;
因为,所以,选项正确;
因为,(
所以与的夹角为,选项D正确.
三.解答题
17.(1) (2)
18.(1) (2)
19.(1) (2) (3)
20.(5分+5分+6分)已知,,函数.
(1)求函数的解析式及其图象的对称中心;
(2)若,且,求的值;
(3)在锐角中,角,,分别为,,三边所对的角,若,,求周长的取值范围.
【答案】(1),函数的对称中心为.
(2) (3)
【解析】(1)因为,
所以
令,则,函数的对称中心为.
(2)因为,即,即
因为,所以,
所以
所以
(3)由可得,即,
又,则,则,所以.
因为,则由正弦定理有
所以
因为为锐角三角形,所以,解得.
所以,则,
所以,则,
所以的周长的取值范围为.
21.(4分+6分+8分)“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:
已知的内角,,所对的边分别为,,,
(1)若,求;
(2)在(1)的条件下,若,设点为的费马点,求;
(3)若,设点为的费马点,,求实数的最小值.
【答案】(1) (2) (3)
【解析】(1)由正弦定理得,即
所以,又,所以;
(2)由(1),所以三角形的三个角都小于,
则由费马点定义可知:
设,由
得:,整理得,
则
(2)因为,
所以,
所以,即
所以或,
当时,为直角三角形,
当,
则
得,在三角形形中不可能成立,所以为的直角三角形,
因为点为的费马点,则
设
则由得;
由余弦定理得
故由得
即,而,故
当且仅当,结合,解得时,等号成立,
又,即有,解得或(舍去),
故实数的最小值为.
2025.4
一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)
1.函数的最小正周期为________.
2.化简:________.
3.已知角的终边经过点,则________.
4.水滴是刘慈欣的科幻小说《三体Ⅱ》中提到的由三体文明使用强互作用力(SIM)材料所制成的宇宙探测器,因为其外形与水滴相似,所以被人类称为水滴.如图所示,水滴是由线段,和圆的优弧围成,其中,恰好与圆弧相切.若圆弧所在圆的半径为2,点到圆弧所在圆圆心的距离为4,则该封闭图形的面积为________.
5.已知,,则在方向上的数量投影是________.
6.已知函数有最小值,则实数的取值范围为________.
7.如图,某侦察飞机沿水平直线匀速飞行.在处观测地面目标,测得俯角.飞行后到达处,此时观测地面目标,测得俯角.又飞行一段时间后到达处,此时观测地面目标,测得俯角的余弦值为,则该侦察飞机由至的飞行时间为________.
8.设为平行四边形的对角线、的交点,为平行四边形所在平面内的一个动点,若,则________.
9.在中,角,,的对边分别为,,,且,若,则对任意,的最小值为________.
10.设,当实数变化时,在区间中至少有个零点,至多有个零点,则________.
11.折扇又名“撒扇”、“纸扇”,是一种用竹木或象牙做扇骨,韧纸或绫绢做扇面的能折叠的扇子,如图1.其展开几何图是如图2的扇形,其中,,
,点在上(包含端点),则的取值范围是________.
12.函数,,,,对任意实数,,当时,都有成立,将函数的图像向左平移个单位得到函数,若函数的最大值为10,则的最小值为________.
二、选择题(本大题共4题,每题5分,共20分)
13.“为锐角”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
14.已知平面向量,不共线,,,,则( )
A.,,三点共线 B.,,三点共线
C.,,三点共线 D.,,三点共线
15.如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则在上的图像大致为( )
A. B.
C. D.
16如图,设,是平面内相交成角的两条数轴,,分别是轴,轴正方向同向的单位向量,若向量,则把有序数对叫做向量在坐标系中的坐标.若在坐标系中,,,则下列结论正确的个数是( )
①;
②,;
③;
④与的夹角为;
A.1个 B.2个 C.3个 D.4个
17.(6分+8分)已知平面向量,,,.
(1)若,求实数的值.
(2)若与的夹角是钝角,求的取值范围.
18.(6分+8分)已知二次函数满足,函数满足,且不等式的解集为.
(1)求的解析式;
(2)若关于的不等式对任意的恒成立,求实数的取值范围.
19.(4分+4分+6分)游客坐在摩天轮的座舱里慢慢的往上转,可以从高处俯瞰四周景色.如图1,该摩天轮最高点距离地面高度为90米,转盘直径为88米,设置有56个座舱,摩天轮上的座舱运动可以近似的看作是质点在圆周上做匀速圆周运动,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要18分钟.如图2,设座舱距离地面最近的位置为点,
(1)游客小明坐上摩天轮的座舱,开始转动分钟后距离地面的高度为米,求在转动一周的过程中,关于的函数解析式,;
(2)坐上摩天轮转动一圈,当距离地面68米及以上高度时游客就能俯瞰全景,大有“一览众山小”之感.小明能有多长时间感受这个过程?
(3)小明在摩天轮上发现朋友小华刚要入舱乘坐摩天轮,而且小华的座舱和自己的座舱之间还有13个座舱,求从小明坐上摩天轮座舱开始计时,到小明运行一周结束计时,问在什么时刻两人距离地面的高度差最大,最大值是多少?
20.(5分+5分+6分)已知,,函数.
(1)求函数的解析式及其图象的对称中心;
(2)若,且,求的值;
(3)在锐角中,角,,分别为,,三边所对的角,若,,求周长的取值范围.
21.(4分+6分+8分)“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:
已知的内角,,所对的边分别为,,,
(1)若,求;
(2)在(1)的条件下,若,设点为的费马点,求;
(3)若,设点为的费马点,,求实数的最小值.
参考答案
一、填空题
1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.; 11. 12.
11.折扇又名“撒扇”、“纸扇”,是一种用竹木或象牙做扇骨,韧纸或绫绢做扇面的能折叠的扇子,如图1.其展开几何图是如图2的扇形,其中,,
,点在上(包含端点),则的取值范围是________.
【答案】
【解析】设是弧的中点,连接,
因为,所以三角形和三角形是等边三角形,
所以四边形是菱形,则,且,
因为点在上(包含端点),所以,
因为,所以
因为,所以
所以,所以的取值范围是.故答案为:.
二、选择题
13.A 14.D 15.B 16.C
15.如图,圆的半径为1,是圆上的定点,是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则在上的图像大致为( )
A.B.
C. D.
【答案】B
【解析】如图:过作于,
则由题意可得:,
在Rt中,,
所以
所以,其图象即为选项.故选:B.
16如图,设,是平面内相交成角的两条数轴,,分别是轴,轴正方向同向的单位向量,若向量,则把有序数对叫做向量在坐标系中的坐标.若在坐标系中,,,则下列结论正确的个数是( )
①;
②,;
③;
④与的夹角为;
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】因为,,且
所以,选项错误;
,所以,选项正确;
因为,所以,选项正确;
因为,(
所以与的夹角为,选项D正确.
三.解答题
17.(1) (2)
18.(1) (2)
19.(1) (2) (3)
20.(5分+5分+6分)已知,,函数.
(1)求函数的解析式及其图象的对称中心;
(2)若,且,求的值;
(3)在锐角中,角,,分别为,,三边所对的角,若,,求周长的取值范围.
【答案】(1),函数的对称中心为.
(2) (3)
【解析】(1)因为,
所以
令,则,函数的对称中心为.
(2)因为,即,即
因为,所以,
所以
所以
(3)由可得,即,
又,则,则,所以.
因为,则由正弦定理有
所以
因为为锐角三角形,所以,解得.
所以,则,
所以,则,
所以的周长的取值范围为.
21.(4分+6分+8分)“费马点”是由十七世纪法国数学家费马提出并征解的一个问题.该问题是:“在一个三角形内求作一点,使其与此三角形的三个顶点的距离之和最小.”意大利数学家托里拆利给出了解答,当的三个内角均小于时,使得的点即为费马点;当有一个内角大于或等于时,最大内角的顶点为费马点.试用以上知识解决下面问题:
已知的内角,,所对的边分别为,,,
(1)若,求;
(2)在(1)的条件下,若,设点为的费马点,求;
(3)若,设点为的费马点,,求实数的最小值.
【答案】(1) (2) (3)
【解析】(1)由正弦定理得,即
所以,又,所以;
(2)由(1),所以三角形的三个角都小于,
则由费马点定义可知:
设,由
得:,整理得,
则
(2)因为,
所以,
所以,即
所以或,
当时,为直角三角形,
当,
则
得,在三角形形中不可能成立,所以为的直角三角形,
因为点为的费马点,则
设
则由得;
由余弦定理得
故由得
即,而,故
当且仅当,结合,解得时,等号成立,
又,即有,解得或(舍去),
故实数的最小值为.
同课章节目录
