北师大版八年级数学下册 第5章 分式与分式方程 复习题--分式的运算(加减乘除)(含解析)
文档属性
| 名称 | 北师大版八年级数学下册 第5章 分式与分式方程 复习题--分式的运算(加减乘除)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 319.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-02 06:55:20 | ||
图片预览




文档简介
第5章《分式与分式方程》复习题--分式的运算(加减乘除)
【题型1 已知分式恒等式求分子(分母)】
1.已知,其中,,,为常数,则 .
2.已知,且,则 .
3.若 ,其中a,b为常数,则 .
4.若,对任意自然数都成立,则 .
【题型2 分式的混合运算】
1.美琪在做数学作业时,不小心将式子中除号后边的代数式污染,即,通过查看答案,答案为,则被污染的代数式为( )
A. B. C. D.
2.如图,若x为正整数,则表示的值的点落在( )
A.段① B.段②
C.段③ D.段④
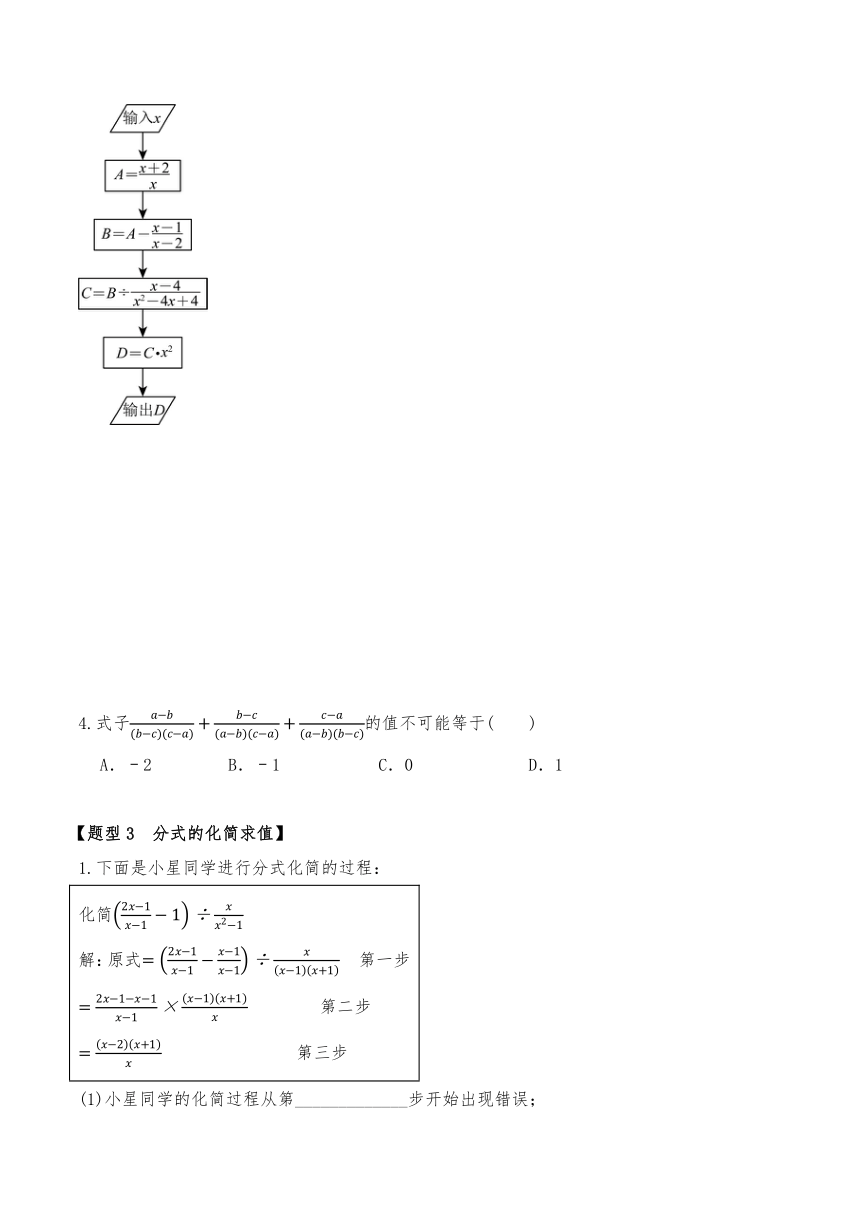
3.根据如图所示的程序,求输出的化简结果.
4.式子的值不可能等于( )
A.﹣2 B.﹣1 C.0 D.1
【题型3 分式的化简求值】
1.下面是小星同学进行分式化简的过程:
化简 解:原式 第一步 第二步 第三步
(1)小星同学的化简过程从第_____________步开始出现错误;
(2)请写出正确的化简过程,并从,0,1,2中选择合适的数带入求值.
2.已知时,代数式的值为( )
A.6 B.-2 C.6或-2 D.0
3.已知
(1)化简W;
(2)若a,2,3恰好是△ABC的三边长,请选取合适的整数a代入W,求出W的值.
4.如图,将四张长、宽分别为的长方形硬纸片拼成一个中间“带孔”的大正方形,已知拼成的大正方形的面积为,中间小正方形的面积为,求的值.
【题型4 比较分式的大小】
1.【阅读理解】在比较两个数或代数式的大小时,解决策略一般是利用“作差法”,即要比较代数式、的大小,只要作出差:若,则;若,则;若,则.
【解决问题】
(1)若,则________0(填、或);
(2)已知,,当时,比较与的大小,并说明理由.
2.两个分式A=,B=﹣,(其中x≠±2,)则A和B的关系是( )
A.A=B B.AB=1 C.A>B D.A+B=0
3.设,,则m,n的关系是( )
A. B. C. D.
4.阅读下列材料,回答问题:爱动脑的小明在学习不等式知识时,查阅资料了解到:当给出不等式时,我们可以将表示为(其中为增量),从而将用代换进一步变形不等式.结合“作差法比较大小”,小明创新出一种证明不等式的方法——增量代换作差法证明不等式.
例如:已知,,求证:.
证明:令,,其中,,
作差得:
∵,
∴,,
∴
所以:.
根据上述材料,解决下列问题:
(1)已知,求证:;
(2)已知,试比较代数式与的大小.
【题型5 分式运算的实际应用】
1.有一块边长为x米的正方形空地,计划按如图所示的方式去种植草皮(图中阴影部分种植草皮).方式一,在正方形空地上留两条宽为2a米的互相垂直的路;方式二,在正方形空地四周各留一块边长为a米的小正方形空地种植树木,现准备用5000元购进草皮.关于哪种方式种植草皮的单价高以及较高的单价是较低的单价的多少倍( )
A.用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
B.用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
C.用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
D.用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
2.有甲,乙两块边长为a米的正方形试验田.负责试验田的杨师傅将试验田的形状进行了调整(如图):沿甲试验田的一边在试验田内修了1米宽的水池,又在邻边增加了1米宽的田地;沿乙试验田的一组邻边在试验田内均修了1米宽的小路.杨师傅在调整后的试验田上种植了某种小麦,其中甲试验田收获了180千克小麦,乙试验田收获了130千克小麦,对于这两块试验田的单位面积产量,下列说法正确的是()
A.甲试验田的单位面积产量高 B.乙试验田的单位面积产量高
C.两块试验田的单位面积产量一样 D.无法判断哪块试验田的单位面积产量高
3.某资料上有这样一段文字:“民用住宅窗户面积应小于地板面积,但窗户面积与地板面积的比值越大,住宅的采光条件会越好.”下面是小刚和小明的对话,请根据对话内容回答问题.
(1)请你通过计算,验证小明的说法;
(2)假设某住宅窗户面积为平方米,地板面积为平方米,且,如果窗户面积和地板面积同时增加1平方米,住宅的采光条件变好了吗?请说明理由.
4.数学来源于生活,生活中处处有数学,用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论.现有克糖水,其中含有克糖,则糖水的浓度(即糖的质量与糖水的质量比)为.
(1)糖水实验一:加入克水,则糖水的浓度为_____________.生活经验告诉我们,糖水加水后会变淡,由此可以写出一个不等式_____________,我们趣称为“糖水不等式”.
(2)糖水实验二:将“糖水实验一”中的“加入克水”改为“加入克糖”,则糖水的浓度为____________.根据生活经验,请你写出一个新的“糖水不等式”____________.
(3)请结合(2)探究得到的结论尝试证明:设为三边的长,求证:.
【题型6 分式运算的规律探究】
1.观察下列各式:
,,,
(1)由此推测________
(2)请你用含字母m的等式表示一般规律(m表示整数)
(3)请直接用(2)的规律计算的值.
2.观察下列等式:,,,…;根据其蕴含的规律可得( )
A. B. C. D.
3.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
……
按照以上规律,解决下列问题:
(1)写出第4个等式:_________;
(2)写出你猜想的第n个等式(用含n的等式表示),并证明.
4.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
【题型7 分式运算的新定义问题】
1.定义:若两个分式A与B满足:,则称A与B这两个分式互为“美妙分式”.若分式与互为“美妙分式”,且a,b均为不等于0的实数,则分式 .
2.定义:若两个分式的差为2,则称这两个分式属于“友好分式组”.
(1)下列3组分式:
①与;②与;③与.其中属于“友好分式组”的有____________(只填序号);
(2)若正实数互为倒数,求证与属于“友好分式组”;
(3)若均为非零实数,且分式与属于“友好分式组”,求分式的值.
3.新定义:若两个分式与的差为(为正整数),则称是的“分式”.例如:,则称分式是分式的“1分式”.根据以上定义,下列选项中说法错误的是( )
A.是的“3分式”
B.若的值为,则是的“2分式”
C.若是的“1分式”,则
D.若与互为倒数,则是的“5分式”
4.定义:代数式中只含有两个字母(如x,y),若把其中的一个字母(x)均换成另一个字母(y),同时另一个字母(y)均换成这个字母(x),若所得代数式是和原代数式相同的代数式,我们称这样的代数式为“对称式”.如,,等.
(1)代数式①,②,③,④中,是对称式的有____.
(2)若关于m,n的代数式(k是常数,)是对称式,求常数k的值.
(3)在(2)的条件下,若,当时,求的值.
【题型8 分式运算的阅读材料题】
1.阅读材料,并解决问题:
我们知道,分子比分母小的分数叫做“真分数”,分子大于或等于分母的分数,叫做“假分数”.类似的,我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于字母的次数时,我们称之为“真分式”.
如,这样的分式就是假分式;再如,这样的分式就是真分式,假分数可以化成(即)带分数的形式,类似的,假分式也可以化为带分式(整式与真分式的和或差)的形式,如:,再如:
,这样,分式就被拆分成了带分式(即一个整式与一个分式的差)的形式.
解决问题:
(1)判断:是真分式还是假分式: (填“真分式”或“假分式”);如果是,化成带分式的形式: ;
(2)思考:当x取什么整数时,分式的值为整数?
(3)探索:当a为何值时,分式有最大值?最大值是多少?
2.【阅读】在处理分式问题时,由于分子的次数不低于分母的次数,在实际运算时往往难度比较大,这时我们可以将分式拆分成一个整式与一个分式的和(差)的形式,通过对简单式子的分析来解决问题,我们称之为分离整式法.
例:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:设,则.
原式
∴.
这样,分式就拆分成一个整式与一个分式的和的形式.
【应用】
(1)使用分离整式法将分式拆分成一个整式与一个分式(分子为整数)的和的形式,则结果为______;
(2)将分式拆分成一个整式与一个分式(分子为整数)的和的形式,则结果为______;
【拓展】
(3)已知分式的值为整数,求正整数x的值.
3.阅读下面的材料:把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例:将分式表示成部分分式.解:设,将等式右边通分,得
,依据题意,得,解得,所以请你适用上面所学到的方法,解决下面的问题:
(1)将分式表示成部分分式;
(2)按照(1)的规律,求的值.
4.阅读下列解题过程:
已知,求的值.
解:由,知,所以,即,
∴,
∴的值为的倒数,即.
以上解法中先将已知等式的两边“取倒数”,然后求出待求式子倒数的值,我们把此题的这种解法叫做“倒数法”,请你利用“倒数法”解决下面问题:
(1)已知,求的值;
(2)已知,求的值.
(3)已知,求的值.
【题型9 整数指数幂】
1.若,则 .
2.已知,,,则a、b、c的大小关系为( )
A. B. C. D.
3.计算a﹣2b2 (a2b﹣2)﹣2正确的结果是( )
A. B. C.a6b6 D.
4.我们知道:,,……,,那么接近于( )
A. B. C. D.
【题型10 利用科学记数法表示小于1的正数】
1.用科学记数法表示0.000032= ,把2.36用小数表示为 .
2.某种细菌直径约为0.00000067mm,若将0.00000067mm用科学记数法表示为mm(n为负整数),则n的值为( )
A.-5 B.-6 C.-7 D.-8
3.地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,地球的体积是太阳体积的倍数约是( )
A.7.1×10-6 B.7.1×10-7
C.1.4×106 D.1.4×107
4.去年11月,在巴黎举行的第27届国际计量大会中宣布引进4个新单位词头,新增的4个词头分别是ronna,quetta,ronto和quecto,其中1ronto,此前,国际单位制最小单位词头为“幺”(yocto).
1幺.一个光子的质量约为幺克.换算后约为 ronto克.
参考答案
【题型1 已知分式恒等式求分子(分母)】
1.6
【分析】由于,利用这个等式首先把已知等式右边通分化简,然后利用分母相同,分式的值相等即可得到分子相等,由此即可得到关于、、、的方程组,解方程组即可求解.
【详解】解:,且,
当时,①
当时,②
当时,③
∵,
即
∴④
联立解之得
、、,
.
故答案为:.
2.2
【分析】本题考查分式的加减,解题的关键是灵活运用所学知识解决问题,学会恒等变形,由题意,可得,因为,所以,推出,由此即可解决问题.
【详解】解析:∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:2.
3.1
【分析】原等式整理变形后得:,可得,求出a、b即可得到答案.
【详解】解:已知等式整理得: ,
∴,
可得,
∴,
∴,
故答案为:1.
4.
【分析】先通分,使得等式左右两边式子分母一致,从而得到,进而得到关于a、b的方程组,解方程得出a、b的值,即可得到答案.
【详解】解:
,
,对任意自然数都成立,
,即,
解得:,
,
故答案为:.
【题型2 分式的混合运算】
1.C
【分析】本题考查了利用平方差公式、提公因式法进行因式分解,分式的化简.熟练掌握利用平方差公式,提公因式法进行因式分解,分式的化简是解题的关键.
利用平方差公式、提公因式法进行因式分解,然后进行除法运算可得化简结果.
【详解】解:由题意知,
被污染的代数式为,
故选:C.
2.B
【分析】先将分式化简、变形为,由x为正整数知,据此可得,从而得出答案.
【详解】解:
=
∵x为正整数,
∴,,
∴,
∴
∴表示的值的点落在②.
故选:B.
3.解:依题意:
.
∴输出的化简结果为
4.C
【分析】根据分式的加减运算,对式子进行化简,然后根据分式有意义,即可得出答案.
【详解】解:
= ,
分式的值不能为0,因为只有a=b=c时,分母才为0,此时分式没意义,
故选:C.
【题型3 分式的化简求值】
1.(1)解:根据题意可得:第二步计算减法时,没有变号,
∴小星同学的化简过程从第二步开始出现错误,
故答案为:二;
(2)解:
;
∵,
∴,
当时,原式.
2.B
【分析】本题考查分式化简求值.先化简分式,再把代入计算即可.
【详解】解:
∵
∴
∵
∴
当时,原式.
故选:B.
3.(1)解:
;
(2)解:∵a,2,3恰好是△ABC的三边长,
∴,
∴,
又∵,,
∴,,
∴a可以取得整数为2或4,
当时,;
当时,.
4.解:由题意得,,,,,
,,
,
,
.
【题型4 比较分式的大小】
1.(1),
,
.
故答案为:.
(2).理由如下:
.
,
,
,
.
2.D
【分析】先把B式进行化简,再判断出A和B的关系即可.
【详解】∵B=
=,
∴A和B互为相反数,即A+B=0.
故选:D.
3.D
【分析】根据分式的运算法则即可求出答案.
【详解】解:
故选:D
4.(1)证明:令,,其中,,
∴
,
∵,,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∴,
∴,
∴
∴
∴
∴,
∴.
【题型5 分式运算的实际应用】
1.A
【分析】先求出每种方式草皮的面积,再5000元除以面积,即可得出答案;列出算式两种草皮单价之比为:,再求出即可.
【详解】解:方式一种植草皮每平方米的单价是5000÷[x2﹣2ax﹣2ax+(2a)2]=(元);
方式二种草皮每平方米的单价是5000÷(x2﹣4a2)==(元),
∵x+2a>x﹣2a,
∴>,
∴用方式一比用方式二种植草皮的单价高,
两种草皮单价之比为:
=
=,
故选:A.
2.D
【分析】根据单位面积产量=产量÷面积,分别表示出甲、乙的单位面积产量,再比较即可.
【详解】解∶甲的单位面积产量为∶(干克/平方米),
乙的单位面积产量为∶(千克/平方米),
则无法判断哪块试验田的单位面积产量高.
故选:D.
3.(1)解:∵住宅窗户面积为3平方米,地板面积为15平方米,∴
∵窗户面积和地板面积同时增加1平方米,∴
∵,∴所以窗户面积和地板面积同时增加1平方米,住宅采光条件会更好.
(2)∵窗户面积为平方米,地板面积为平方米,∴
∵窗户面积和地板面积同时增加1平方米,∴
∴,
∵,∴,,
∴,∴,
∴窗户面积和地板面积同时增加1平方米,住宅的采光条件会更好.
4.(1)解: 由题意得,加入克水,糖水为克,
∴糖水的浓度为;
∵糖水加水后会变淡,即糖水的浓度变小,
∴;
故答案为:;.
(2)解:由题意得,加入克糖,糖水为克,糖为克,
∴糖水的浓度为;
假设新的“糖水不等式”为,下面用数学知识证明:
,其中,
∴,
∴,即,
故答案为:;.
(3)证明:由(2)可知
.
【题型6 分式运算的规律探究】
1.(1)解:;
(2)解:由()可得
;
(3)解:
.
2.D
【分析】归纳总结得到一般性规律,即可得到结果.
【详解】由a1=n,得到:
以为循环节3次一循环,
∵2013÷3=671,
∴
故选D.
3.(1)解:第1个等式:,
第2个等式:,
第3个等式:,
∴第4个等式为:;
故答案为:;
(2)解:第n个等式为:,
证明:∵左边,
右边左边,
∴.
4.(1)解:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第6个等式:;
故答案为:;
(2)猜想:第个等式:,
证明:∵
,
∴成立.
故答案为:.
【题型7 分式运算的新定义问题】
1.或
【分析】本题考查了分式的加减法和实数的性质,绝对值的意义,熟练掌握分式加减法的法则,对新定义的理解是解题关键.
根据分式与互为“美妙分式”,得到,求出①,②,分别把①②代入分式中求出结果即可.
【详解】与互为“美妙分式”,
,
,
或,
或,
、均为不等于的实数,
①,②,
把①代入,
把②代入,
综上:分式的值为或.
故答案为:或.
2.(1)解:①
② ;
③
则
∴属于“友好分式组”的有②③.
故答案为:②③
(2)∵a,b互为倒数,
∴,,
∴
∴与属于“友好分式组”
(3)
∵a,b均为非零实数,且分式与属于“友好分式组”,
或
把①代入
把②代入
∴的值为或
3.C
【分析】根据新定义运算逐个验证正确与否即可.
【详解】A、,A说法正确;
B、,B说法正确;
C、由已知条件得:,化简得:,C说法错误;
D、由已知得:,,D说法正确.
故选:C.
4.(1)解:对于①,将互换后,得到,不符合题意;
对于②,将互换后,得到,符合题意;
对于③,将互换后,得到,符合题意;
对于④,将互换后,得到,符合题意;
故答案为:②③④
(2)∵是对称式,
∴,
∴,
∴,
∴,
∵,
∴;
(3)由题意,得:
∴,
∴,
∴,
∴,
∴.
【题型8 分式运算的阅读材料题】
1.(1)解:分子,分母的次数相等,
故答案为:假分式;
(2)解:原式,
当时,原式为整数;
(3)解:,
,
时,有最小值,值最大,
,即时,,
当a为2,分式有最大值,最大值是5.
2.(1)解: ,
故答案为:;
(2)设,则,
∴
∴,
故答案为:;
(3)设,则,
∴
∵分式的值为整数,且x是正整数,∴,,
由,得或
由,得或(舍)
∴正整数x的值为4或2或16.
3.(1)解:设,
∴,
∴,
∴.
(2)
;
4.(1)解:由,知,所以,即.
∴.
∴的值为2的倒数,即.
(2)由,得到,
即,
∴,
则;
(3)根据题意得:,,,
∴,
∴
∴
∴.
【题型9 整数指数幂】
1.
【分析】根据完全平方公式进行计算即可求解.
【详解】解:∵,
∴,
∴,
∴,
∴,
故答案为:.
2.C
【分析】先计算幂的乘方、负整数指数幂、零指数幂,再进行有理数的大小比较即可.
【详解】解:,,,
∴,
故选:C.
3.B
【分析】根据负整数指数幂,积的乘方,同底数幂的乘法,进行幂的混合运算即可求解.
【详解】解:原式=,
故选B.
4.B
【分析】由负整数指数幂的含义结合整数指数幂的运算可得:再分别把各选项变形,再比较即可得到答案.
【详解】解:
而
即
是一个10位整数,最高位的数字为1,
是一个10位整数,最高位的数字为1,是一个11位整数,最高位的数字为1,
所以更接近
所以最接近
故选B
【题型10 利用科学记数法表示小于1的正数】
1. 0.0000236
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定,据此可得.
【详解】用科学记数法表示0.000032=3.2×10-5,用小数表示2.36×10-5=0.0000236,
故答案为:3.2×10-5,0.0000236.
2.C
【详解】解:∵0.000 000 67mm=6.7×10-7
∴n=-7
故选:C
3.B
【分析】直接利用整式的除法运算法则结合科学记数法求出答案.
【详解】解:∵地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,
∴地球的体积约是太阳体积的倍数是:1012÷1.4×1018≈7.1×10﹣7.
故选:B
4.
【分析】运用科学记数法的运算法则解答即可.
【详解】一个光子的质量约为幺克.换算后约为 ronto克
故答案为.
【题型1 已知分式恒等式求分子(分母)】
1.已知,其中,,,为常数,则 .
2.已知,且,则 .
3.若 ,其中a,b为常数,则 .
4.若,对任意自然数都成立,则 .
【题型2 分式的混合运算】
1.美琪在做数学作业时,不小心将式子中除号后边的代数式污染,即,通过查看答案,答案为,则被污染的代数式为( )
A. B. C. D.
2.如图,若x为正整数,则表示的值的点落在( )
A.段① B.段②
C.段③ D.段④
3.根据如图所示的程序,求输出的化简结果.
4.式子的值不可能等于( )
A.﹣2 B.﹣1 C.0 D.1
【题型3 分式的化简求值】
1.下面是小星同学进行分式化简的过程:
化简 解:原式 第一步 第二步 第三步
(1)小星同学的化简过程从第_____________步开始出现错误;
(2)请写出正确的化简过程,并从,0,1,2中选择合适的数带入求值.
2.已知时,代数式的值为( )
A.6 B.-2 C.6或-2 D.0
3.已知
(1)化简W;
(2)若a,2,3恰好是△ABC的三边长,请选取合适的整数a代入W,求出W的值.
4.如图,将四张长、宽分别为的长方形硬纸片拼成一个中间“带孔”的大正方形,已知拼成的大正方形的面积为,中间小正方形的面积为,求的值.
【题型4 比较分式的大小】
1.【阅读理解】在比较两个数或代数式的大小时,解决策略一般是利用“作差法”,即要比较代数式、的大小,只要作出差:若,则;若,则;若,则.
【解决问题】
(1)若,则________0(填、或);
(2)已知,,当时,比较与的大小,并说明理由.
2.两个分式A=,B=﹣,(其中x≠±2,)则A和B的关系是( )
A.A=B B.AB=1 C.A>B D.A+B=0
3.设,,则m,n的关系是( )
A. B. C. D.
4.阅读下列材料,回答问题:爱动脑的小明在学习不等式知识时,查阅资料了解到:当给出不等式时,我们可以将表示为(其中为增量),从而将用代换进一步变形不等式.结合“作差法比较大小”,小明创新出一种证明不等式的方法——增量代换作差法证明不等式.
例如:已知,,求证:.
证明:令,,其中,,
作差得:
∵,
∴,,
∴
所以:.
根据上述材料,解决下列问题:
(1)已知,求证:;
(2)已知,试比较代数式与的大小.
【题型5 分式运算的实际应用】
1.有一块边长为x米的正方形空地,计划按如图所示的方式去种植草皮(图中阴影部分种植草皮).方式一,在正方形空地上留两条宽为2a米的互相垂直的路;方式二,在正方形空地四周各留一块边长为a米的小正方形空地种植树木,现准备用5000元购进草皮.关于哪种方式种植草皮的单价高以及较高的单价是较低的单价的多少倍( )
A.用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
B.用方式一比用方式二种植草皮的单价高,且较高的单价是较低的单价的倍
C.用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
D.用方式二比用方式一种植草皮的单价高,且较高的单价是较低的单价的倍
2.有甲,乙两块边长为a米的正方形试验田.负责试验田的杨师傅将试验田的形状进行了调整(如图):沿甲试验田的一边在试验田内修了1米宽的水池,又在邻边增加了1米宽的田地;沿乙试验田的一组邻边在试验田内均修了1米宽的小路.杨师傅在调整后的试验田上种植了某种小麦,其中甲试验田收获了180千克小麦,乙试验田收获了130千克小麦,对于这两块试验田的单位面积产量,下列说法正确的是()
A.甲试验田的单位面积产量高 B.乙试验田的单位面积产量高
C.两块试验田的单位面积产量一样 D.无法判断哪块试验田的单位面积产量高
3.某资料上有这样一段文字:“民用住宅窗户面积应小于地板面积,但窗户面积与地板面积的比值越大,住宅的采光条件会越好.”下面是小刚和小明的对话,请根据对话内容回答问题.
(1)请你通过计算,验证小明的说法;
(2)假设某住宅窗户面积为平方米,地板面积为平方米,且,如果窗户面积和地板面积同时增加1平方米,住宅的采光条件变好了吗?请说明理由.
4.数学来源于生活,生活中处处有数学,用我们平时喝的糖水做“糖水实验”也能验证发现一些数学结论.现有克糖水,其中含有克糖,则糖水的浓度(即糖的质量与糖水的质量比)为.
(1)糖水实验一:加入克水,则糖水的浓度为_____________.生活经验告诉我们,糖水加水后会变淡,由此可以写出一个不等式_____________,我们趣称为“糖水不等式”.
(2)糖水实验二:将“糖水实验一”中的“加入克水”改为“加入克糖”,则糖水的浓度为____________.根据生活经验,请你写出一个新的“糖水不等式”____________.
(3)请结合(2)探究得到的结论尝试证明:设为三边的长,求证:.
【题型6 分式运算的规律探究】
1.观察下列各式:
,,,
(1)由此推测________
(2)请你用含字母m的等式表示一般规律(m表示整数)
(3)请直接用(2)的规律计算的值.
2.观察下列等式:,,,…;根据其蕴含的规律可得( )
A. B. C. D.
3.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
……
按照以上规律,解决下列问题:
(1)写出第4个等式:_________;
(2)写出你猜想的第n个等式(用含n的等式表示),并证明.
4.观察以下等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
按照以上规律,解决下列问题:
(1)写出第5个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
【题型7 分式运算的新定义问题】
1.定义:若两个分式A与B满足:,则称A与B这两个分式互为“美妙分式”.若分式与互为“美妙分式”,且a,b均为不等于0的实数,则分式 .
2.定义:若两个分式的差为2,则称这两个分式属于“友好分式组”.
(1)下列3组分式:
①与;②与;③与.其中属于“友好分式组”的有____________(只填序号);
(2)若正实数互为倒数,求证与属于“友好分式组”;
(3)若均为非零实数,且分式与属于“友好分式组”,求分式的值.
3.新定义:若两个分式与的差为(为正整数),则称是的“分式”.例如:,则称分式是分式的“1分式”.根据以上定义,下列选项中说法错误的是( )
A.是的“3分式”
B.若的值为,则是的“2分式”
C.若是的“1分式”,则
D.若与互为倒数,则是的“5分式”
4.定义:代数式中只含有两个字母(如x,y),若把其中的一个字母(x)均换成另一个字母(y),同时另一个字母(y)均换成这个字母(x),若所得代数式是和原代数式相同的代数式,我们称这样的代数式为“对称式”.如,,等.
(1)代数式①,②,③,④中,是对称式的有____.
(2)若关于m,n的代数式(k是常数,)是对称式,求常数k的值.
(3)在(2)的条件下,若,当时,求的值.
【题型8 分式运算的阅读材料题】
1.阅读材料,并解决问题:
我们知道,分子比分母小的分数叫做“真分数”,分子大于或等于分母的分数,叫做“假分数”.类似的,我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于字母的次数时,我们称之为“真分式”.
如,这样的分式就是假分式;再如,这样的分式就是真分式,假分数可以化成(即)带分数的形式,类似的,假分式也可以化为带分式(整式与真分式的和或差)的形式,如:,再如:
,这样,分式就被拆分成了带分式(即一个整式与一个分式的差)的形式.
解决问题:
(1)判断:是真分式还是假分式: (填“真分式”或“假分式”);如果是,化成带分式的形式: ;
(2)思考:当x取什么整数时,分式的值为整数?
(3)探索:当a为何值时,分式有最大值?最大值是多少?
2.【阅读】在处理分式问题时,由于分子的次数不低于分母的次数,在实际运算时往往难度比较大,这时我们可以将分式拆分成一个整式与一个分式的和(差)的形式,通过对简单式子的分析来解决问题,我们称之为分离整式法.
例:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:设,则.
原式
∴.
这样,分式就拆分成一个整式与一个分式的和的形式.
【应用】
(1)使用分离整式法将分式拆分成一个整式与一个分式(分子为整数)的和的形式,则结果为______;
(2)将分式拆分成一个整式与一个分式(分子为整数)的和的形式,则结果为______;
【拓展】
(3)已知分式的值为整数,求正整数x的值.
3.阅读下面的材料:把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例:将分式表示成部分分式.解:设,将等式右边通分,得
,依据题意,得,解得,所以请你适用上面所学到的方法,解决下面的问题:
(1)将分式表示成部分分式;
(2)按照(1)的规律,求的值.
4.阅读下列解题过程:
已知,求的值.
解:由,知,所以,即,
∴,
∴的值为的倒数,即.
以上解法中先将已知等式的两边“取倒数”,然后求出待求式子倒数的值,我们把此题的这种解法叫做“倒数法”,请你利用“倒数法”解决下面问题:
(1)已知,求的值;
(2)已知,求的值.
(3)已知,求的值.
【题型9 整数指数幂】
1.若,则 .
2.已知,,,则a、b、c的大小关系为( )
A. B. C. D.
3.计算a﹣2b2 (a2b﹣2)﹣2正确的结果是( )
A. B. C.a6b6 D.
4.我们知道:,,……,,那么接近于( )
A. B. C. D.
【题型10 利用科学记数法表示小于1的正数】
1.用科学记数法表示0.000032= ,把2.36用小数表示为 .
2.某种细菌直径约为0.00000067mm,若将0.00000067mm用科学记数法表示为mm(n为负整数),则n的值为( )
A.-5 B.-6 C.-7 D.-8
3.地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,地球的体积是太阳体积的倍数约是( )
A.7.1×10-6 B.7.1×10-7
C.1.4×106 D.1.4×107
4.去年11月,在巴黎举行的第27届国际计量大会中宣布引进4个新单位词头,新增的4个词头分别是ronna,quetta,ronto和quecto,其中1ronto,此前,国际单位制最小单位词头为“幺”(yocto).
1幺.一个光子的质量约为幺克.换算后约为 ronto克.
参考答案
【题型1 已知分式恒等式求分子(分母)】
1.6
【分析】由于,利用这个等式首先把已知等式右边通分化简,然后利用分母相同,分式的值相等即可得到分子相等,由此即可得到关于、、、的方程组,解方程组即可求解.
【详解】解:,且,
当时,①
当时,②
当时,③
∵,
即
∴④
联立解之得
、、,
.
故答案为:.
2.2
【分析】本题考查分式的加减,解题的关键是灵活运用所学知识解决问题,学会恒等变形,由题意,可得,因为,所以,推出,由此即可解决问题.
【详解】解析:∵,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:2.
3.1
【分析】原等式整理变形后得:,可得,求出a、b即可得到答案.
【详解】解:已知等式整理得: ,
∴,
可得,
∴,
∴,
故答案为:1.
4.
【分析】先通分,使得等式左右两边式子分母一致,从而得到,进而得到关于a、b的方程组,解方程得出a、b的值,即可得到答案.
【详解】解:
,
,对任意自然数都成立,
,即,
解得:,
,
故答案为:.
【题型2 分式的混合运算】
1.C
【分析】本题考查了利用平方差公式、提公因式法进行因式分解,分式的化简.熟练掌握利用平方差公式,提公因式法进行因式分解,分式的化简是解题的关键.
利用平方差公式、提公因式法进行因式分解,然后进行除法运算可得化简结果.
【详解】解:由题意知,
被污染的代数式为,
故选:C.
2.B
【分析】先将分式化简、变形为,由x为正整数知,据此可得,从而得出答案.
【详解】解:
=
∵x为正整数,
∴,,
∴,
∴
∴表示的值的点落在②.
故选:B.
3.解:依题意:
.
∴输出的化简结果为
4.C
【分析】根据分式的加减运算,对式子进行化简,然后根据分式有意义,即可得出答案.
【详解】解:
= ,
分式的值不能为0,因为只有a=b=c时,分母才为0,此时分式没意义,
故选:C.
【题型3 分式的化简求值】
1.(1)解:根据题意可得:第二步计算减法时,没有变号,
∴小星同学的化简过程从第二步开始出现错误,
故答案为:二;
(2)解:
;
∵,
∴,
当时,原式.
2.B
【分析】本题考查分式化简求值.先化简分式,再把代入计算即可.
【详解】解:
∵
∴
∵
∴
当时,原式.
故选:B.
3.(1)解:
;
(2)解:∵a,2,3恰好是△ABC的三边长,
∴,
∴,
又∵,,
∴,,
∴a可以取得整数为2或4,
当时,;
当时,.
4.解:由题意得,,,,,
,,
,
,
.
【题型4 比较分式的大小】
1.(1),
,
.
故答案为:.
(2).理由如下:
.
,
,
,
.
2.D
【分析】先把B式进行化简,再判断出A和B的关系即可.
【详解】∵B=
=,
∴A和B互为相反数,即A+B=0.
故选:D.
3.D
【分析】根据分式的运算法则即可求出答案.
【详解】解:
故选:D
4.(1)证明:令,,其中,,
∴
,
∵,,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∴,
∴,
∴
∴
∴
∴,
∴.
【题型5 分式运算的实际应用】
1.A
【分析】先求出每种方式草皮的面积,再5000元除以面积,即可得出答案;列出算式两种草皮单价之比为:,再求出即可.
【详解】解:方式一种植草皮每平方米的单价是5000÷[x2﹣2ax﹣2ax+(2a)2]=(元);
方式二种草皮每平方米的单价是5000÷(x2﹣4a2)==(元),
∵x+2a>x﹣2a,
∴>,
∴用方式一比用方式二种植草皮的单价高,
两种草皮单价之比为:
=
=,
故选:A.
2.D
【分析】根据单位面积产量=产量÷面积,分别表示出甲、乙的单位面积产量,再比较即可.
【详解】解∶甲的单位面积产量为∶(干克/平方米),
乙的单位面积产量为∶(千克/平方米),
则无法判断哪块试验田的单位面积产量高.
故选:D.
3.(1)解:∵住宅窗户面积为3平方米,地板面积为15平方米,∴
∵窗户面积和地板面积同时增加1平方米,∴
∵,∴所以窗户面积和地板面积同时增加1平方米,住宅采光条件会更好.
(2)∵窗户面积为平方米,地板面积为平方米,∴
∵窗户面积和地板面积同时增加1平方米,∴
∴,
∵,∴,,
∴,∴,
∴窗户面积和地板面积同时增加1平方米,住宅的采光条件会更好.
4.(1)解: 由题意得,加入克水,糖水为克,
∴糖水的浓度为;
∵糖水加水后会变淡,即糖水的浓度变小,
∴;
故答案为:;.
(2)解:由题意得,加入克糖,糖水为克,糖为克,
∴糖水的浓度为;
假设新的“糖水不等式”为,下面用数学知识证明:
,其中,
∴,
∴,即,
故答案为:;.
(3)证明:由(2)可知
.
【题型6 分式运算的规律探究】
1.(1)解:;
(2)解:由()可得
;
(3)解:
.
2.D
【分析】归纳总结得到一般性规律,即可得到结果.
【详解】由a1=n,得到:
以为循环节3次一循环,
∵2013÷3=671,
∴
故选D.
3.(1)解:第1个等式:,
第2个等式:,
第3个等式:,
∴第4个等式为:;
故答案为:;
(2)解:第n个等式为:,
证明:∵左边,
右边左边,
∴.
4.(1)解:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
第6个等式:;
故答案为:;
(2)猜想:第个等式:,
证明:∵
,
∴成立.
故答案为:.
【题型7 分式运算的新定义问题】
1.或
【分析】本题考查了分式的加减法和实数的性质,绝对值的意义,熟练掌握分式加减法的法则,对新定义的理解是解题关键.
根据分式与互为“美妙分式”,得到,求出①,②,分别把①②代入分式中求出结果即可.
【详解】与互为“美妙分式”,
,
,
或,
或,
、均为不等于的实数,
①,②,
把①代入,
把②代入,
综上:分式的值为或.
故答案为:或.
2.(1)解:①
② ;
③
则
∴属于“友好分式组”的有②③.
故答案为:②③
(2)∵a,b互为倒数,
∴,,
∴
∴与属于“友好分式组”
(3)
∵a,b均为非零实数,且分式与属于“友好分式组”,
或
把①代入
把②代入
∴的值为或
3.C
【分析】根据新定义运算逐个验证正确与否即可.
【详解】A、,A说法正确;
B、,B说法正确;
C、由已知条件得:,化简得:,C说法错误;
D、由已知得:,,D说法正确.
故选:C.
4.(1)解:对于①,将互换后,得到,不符合题意;
对于②,将互换后,得到,符合题意;
对于③,将互换后,得到,符合题意;
对于④,将互换后,得到,符合题意;
故答案为:②③④
(2)∵是对称式,
∴,
∴,
∴,
∴,
∵,
∴;
(3)由题意,得:
∴,
∴,
∴,
∴,
∴.
【题型8 分式运算的阅读材料题】
1.(1)解:分子,分母的次数相等,
故答案为:假分式;
(2)解:原式,
当时,原式为整数;
(3)解:,
,
时,有最小值,值最大,
,即时,,
当a为2,分式有最大值,最大值是5.
2.(1)解: ,
故答案为:;
(2)设,则,
∴
∴,
故答案为:;
(3)设,则,
∴
∵分式的值为整数,且x是正整数,∴,,
由,得或
由,得或(舍)
∴正整数x的值为4或2或16.
3.(1)解:设,
∴,
∴,
∴.
(2)
;
4.(1)解:由,知,所以,即.
∴.
∴的值为2的倒数,即.
(2)由,得到,
即,
∴,
则;
(3)根据题意得:,,,
∴,
∴
∴
∴.
【题型9 整数指数幂】
1.
【分析】根据完全平方公式进行计算即可求解.
【详解】解:∵,
∴,
∴,
∴,
∴,
故答案为:.
2.C
【分析】先计算幂的乘方、负整数指数幂、零指数幂,再进行有理数的大小比较即可.
【详解】解:,,,
∴,
故选:C.
3.B
【分析】根据负整数指数幂,积的乘方,同底数幂的乘法,进行幂的混合运算即可求解.
【详解】解:原式=,
故选B.
4.B
【分析】由负整数指数幂的含义结合整数指数幂的运算可得:再分别把各选项变形,再比较即可得到答案.
【详解】解:
而
即
是一个10位整数,最高位的数字为1,
是一个10位整数,最高位的数字为1,是一个11位整数,最高位的数字为1,
所以更接近
所以最接近
故选B
【题型10 利用科学记数法表示小于1的正数】
1. 0.0000236
【分析】绝对值小于1的负数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定,据此可得.
【详解】用科学记数法表示0.000032=3.2×10-5,用小数表示2.36×10-5=0.0000236,
故答案为:3.2×10-5,0.0000236.
2.C
【详解】解:∵0.000 000 67mm=6.7×10-7
∴n=-7
故选:C
3.B
【分析】直接利用整式的除法运算法则结合科学记数法求出答案.
【详解】解:∵地球的体积约为1012立方千米,太阳的体积约为1.4×1018立方千米,
∴地球的体积约是太阳体积的倍数是:1012÷1.4×1018≈7.1×10﹣7.
故选:B
4.
【分析】运用科学记数法的运算法则解答即可.
【详解】一个光子的质量约为幺克.换算后约为 ronto克
故答案为.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
