浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 15:52:01 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.要使式子有意义,则x的取值范围是( )
A.x≥1 B.x≤1 C.x≠1 D.x≤﹣1
2.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
3.若长和宽分别是a,b的长方形的周长为10,面积为6,则a2b+ab2的值为( )
A.14 B.16 C.20 D.30
4.计算的结果是( )
A. B. C. D.
5.随着全球经济发展,环境保护受到国家的重视.张老师购置了新能源电动汽车,这样他驾车上班比乘公交车所需的时间少用了12分钟,张老师家到学校的距离为8千米.已知电动汽车的平均速度是公交车的2.5倍,若设乘公交车平均每小时走x千米,则可列方程为( )
A. B.
C. D.
6.若关于x的分式方程无解,则a的值为( )
A. B.﹣1 C.或0 D.0或﹣1
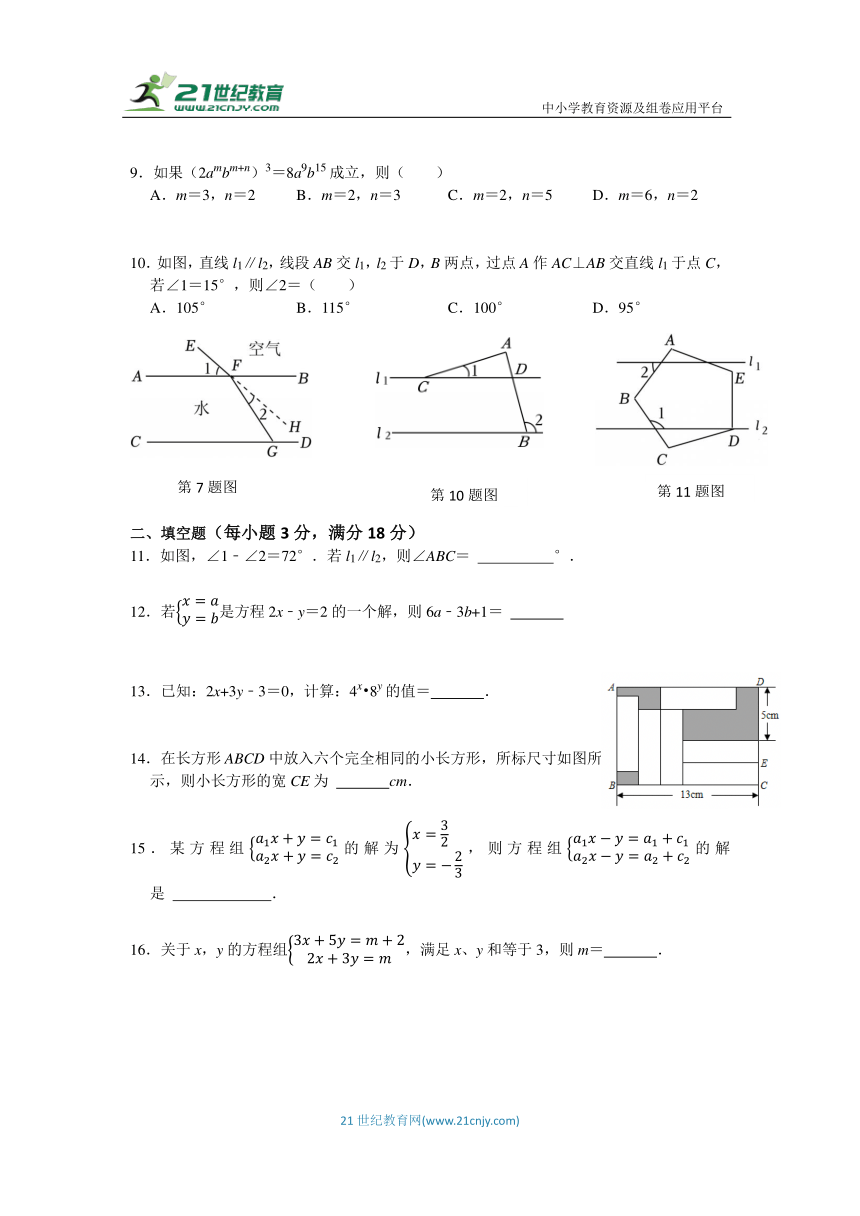
7.光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若∠1=42°,∠2=16°,则∠CGF的度数是( )
A.58° B.48° C.26° D.32°
8.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
9.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
10.如图,直线l1∥l2,线段AB交l1,l2于D,B两点,过点A作AC⊥AB交直线l1于点C,若∠1=15°,则∠2=( )
A.105° B.115° C.100° D.95°
二、填空题(每小题3分,满分18分)
11.如图,∠1﹣∠2=72°.若l1∥l2,则∠ABC= °.
12.若是方程2x﹣y=2的一个解,则6a﹣3b+1=
13.已知:2x+3y﹣3=0,计算:4x 8y的值= .
14.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
15.某方程组的解为,则方程组的解是 .
16.关于x,y的方程组,满足x、y和等于3,则m= .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
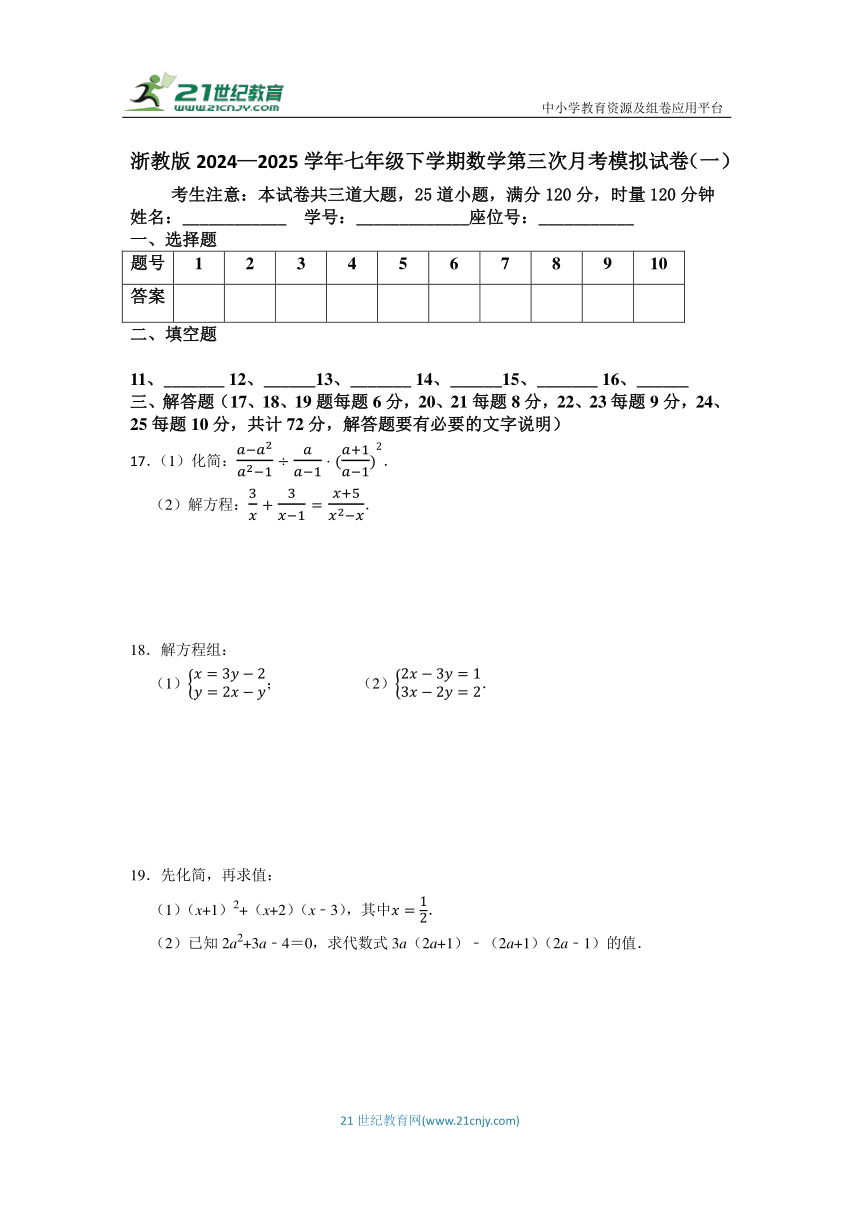
17.(1)化简:.
(2)解方程:.
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,已知∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2:∠3=1:4,求∠BOF的度数.
21.某校组织七年级350名学生去研学,已知1辆A型车和2辆B型车可以载学生110人;3辆A型车和1辆B型车可以载学生130人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好送完学生,并且租车费用最少?
22.已知,关于x的分式方程1.
(1)当a=2,b=1时,求分式方程的解;
(2)当a=1时,求b为何值时分式方程1无解;
(3)若a=3b,且a、b为正整数,当分式方程1的解为整数时,求b的值.
23.我们把形如(m,n不为零),且两个解分别为x1=m,x2=n的方程称为“十字分式方程”.
例如为十字分式方程,可化为,∴x1=2,x2=3;
再如为十字分式方程,可化为,∴x1=﹣1,x2=﹣7.应用上面的结论解答下列问题:
(1)若为十字分式方程,则x1= ,x2= .
(2)若十字分式方程的两个解分别为x1=a,x2=b,求的值.
(3)若关于x的十字分式方程的两个解分别为x1,x2(k>2,x1>x2),求的值.
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.我们在学习“从面积到乘法公式”时,曾用两种不同的方法计算同一个图形的面积,探索了完全平方公式:(a+b)2=a2+2ab+b2(如图1).
(1)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
拓展应用:根据(1)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
(2)若,且x>y,求x﹣y的值;
(3)若(2025﹣m)2+(m﹣2024)2=7,求(2025﹣m)(m﹣2024)的值;
(4)如图3,在△BCE中,∠BCE=90°,CE=8,点M在边BC上,CM=3,在边CE上取一点Q,使BM=EQ,分别以BC,CQ为边在△BCE外部作正方形ABCD和正方形COPQ,连接BQ,若△BCQ的面积等于,设BM=x(x>0),求正方形ABCD和正方形COPQ的面积和.
参考答案
一、选择题
1—10:CBDDD CADAB
二、填空题
11.【解答】解:延长AB交直线l2于点F,设BC与直线l2交于点G,
∵l1∥l2,
∴∠2=∠AFG,
∵∠1是△BFG的一个外角,
∴∠FBG=∠1﹣∠AFG=∠1﹣∠2,
∵∠1﹣∠2=72°,
∴∠FBG=72°,
∴∠ABG=180°﹣∠FBG=108°,
故答案为:108.
12.【解答】解:把代入方程2x﹣y=2得:2a﹣b=2,
∴6a﹣3b+1
=3(2a﹣b)+1
=3×2+1
=6+1
=7,
故答案为:7.
13.【解答】解:∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x 8y=22x 23y=22x+3y=23=8,
故答案为:8.
14.【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
15.【解答】解:将方程组变形为,
∵方程组的解为,
∴方程组的解为,即,
故答案为:.
16.【解答】解:,
由①﹣②得:x+2y=2③,
由x、y和等于3得到x+y=3,
联立③、④得方程组:,
解之得:,
把代入①得:3×4+5×(﹣1)=m+2,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1)原式
;
(2),
3(x﹣1)+3x=x+5,
3x﹣3+3x=x+5,
5x=8,
,
经检验:是方程的解.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵OA,OB分别平分∠COE和∠DOE,
∴∠AOE∠COE,∠BOEDOE,
∴∠AOB=∠AOE+∠BOE(∠COE+∠DOE)=90°,
∴∠AOC+∠2=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD.
(2)解:设∠2=x,则∠3=4x,
∵OB分别平分∠DOE,
∴∠BOE=∠2=x,
∵∠3+∠2+∠BOE=180°,
∴4x+x+x=180°,
∴x=30°,
∴∠BOF=∠3+∠2=5x=150°.
21.【解答】解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人.
根据题意,得,
解得,
∴每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租用A型车a辆,则租用B型车辆.
根据题意,租车费用W=1000a+1200100a+10500,
∵100>0,
∴W随a的减小而减小,
∵a≥0(a为整数),且为非负整数,
∴当a=1时,8,W取最小值,
∴租用A型车1辆,租用B型车8辆使得恰好送完学生,并且租车费用最少.
22.【解答】解:(1)把a=2,b=1代入分式方程 中,得,
方程两边同时乘以(2x+3)(x﹣5),
2(x﹣5)﹣(1﹣x)(2x+3)=(2x+3)(x﹣5),
2x2+3x﹣13=2x2﹣7x﹣15,
10x=﹣2,
x,
检验:把x 代入(2x+3)(x﹣5)≠0,所以原分式方程的解是x.
答:分式方程的解是x.
(2)把a=1代入分式方程 得,
方程两边同时乘以(2x+3)(x﹣5),
(x﹣5)﹣(b﹣x)(2x+3)=(2x+3)(x﹣5),
x﹣5+2x2+3x﹣2bx﹣3b=2x2﹣7x﹣15,
(11﹣2b)x=3b﹣10,
①当11﹣2b=0时,即,方程无解;
②当11﹣2b≠0时,,
时,分式方程无解,即,b不存在;
x=5时,分式方程无解,即,b=5.
综上所述,或b=5时,分式方程 无解.
(3)把a=3b代入分式方程 中,得:
方程两边同时乘以(2x+3)(x﹣5),
3b(x﹣5)+(x﹣b)(2x+3)=(2x+3)(x﹣5),
整理得:(10+b)x=18b﹣15,
∴,
∵,且b为正整数,x为整数,
∴10+b必为195的因数,10+b≥11,
∵195=3×5×13,
∴195的因数有1、3、5、13、15、39、65、195,
但1、3、5 小于11,不合题意,故10+b可以取13、15、39、65、195这五个数.
对应地,方程的解x为3、5、13、15、17,
由于x=5为分式方程的增根,故应舍去.
对应地,b只可以取3、29、55、185,
所以满足条件的b可取3、29、55、185这四个数.
23.【解答】解:(1)由题意,∵x4=1+3,
∴x1=1,x2=3.
故答案为:1;3.
(2)由题意,∵十字分式方程的两个解分别为x1=a,x2=b,
∴ab=﹣2,a+b=﹣3.
又∵11,
∴1.
(3)由题意,∵,
∴x﹣12025k﹣2025.
∴x﹣12024k﹣2025+k.
又∵关于x的十字分式方程的两个解分别为x1,x2(k>2,x1>x2),
∴x1﹣1=2024k﹣2025,x2﹣1=k.
∴x1=2024k﹣2024,x2=k+1.
∴2024.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)由图可知:大正方形的面积等于4个长方形的面积加上阴影正方形的面积,
∴(a+b)2=(a﹣b)2+4ab;
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)可得(x﹣y)2=(x+y)2﹣4xy,
∴(x﹣y)2=(x+y)2﹣4xy,
∵x>y,
∴x﹣y=3;
(3)由条件可知2ab=(a+b)2﹣(a2+b2),
∵(2025﹣m)2+(m﹣2024)2=7,
∴2(2025﹣m)(m﹣2024)
=(2025﹣m+m﹣2024)2﹣[(2025﹣m)2+(m﹣2024)2]
=1﹣7
=﹣6,
∴原式=﹣3;
(4)设BM=x,则BM=EQ=x,
∴CM=3,CE=8,
CQ=CE﹣EQ=8﹣x,BC=BM+CM=3+x,
∵,
∴(8﹣x)(3+x)=21,
令8﹣x=a,x+3=b,
∴a+b=11,ab=21,
∴正方形ABCD和正方形COPQ的面积和:
=a2+b2=(a+b)2﹣2ab=112﹣2×21=121﹣42=79.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.要使式子有意义,则x的取值范围是( )
A.x≥1 B.x≤1 C.x≠1 D.x≤﹣1
2.下列各式不能使用平方差公式的是( )
A.(2a+3b)(2a﹣3b) B.(﹣2a+3b)(3b﹣2a)
C.(﹣2a+3b)(﹣2a﹣3b) D.(2a﹣3b)(﹣2a﹣3b)
3.若长和宽分别是a,b的长方形的周长为10,面积为6,则a2b+ab2的值为( )
A.14 B.16 C.20 D.30
4.计算的结果是( )
A. B. C. D.
5.随着全球经济发展,环境保护受到国家的重视.张老师购置了新能源电动汽车,这样他驾车上班比乘公交车所需的时间少用了12分钟,张老师家到学校的距离为8千米.已知电动汽车的平均速度是公交车的2.5倍,若设乘公交车平均每小时走x千米,则可列方程为( )
A. B.
C. D.
6.若关于x的分式方程无解,则a的值为( )
A. B.﹣1 C.或0 D.0或﹣1
7.光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若∠1=42°,∠2=16°,则∠CGF的度数是( )
A.58° B.48° C.26° D.32°
8.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
9.如果(2ambm+n)3=8a9b15成立,则( )
A.m=3,n=2 B.m=2,n=3 C.m=2,n=5 D.m=6,n=2
10.如图,直线l1∥l2,线段AB交l1,l2于D,B两点,过点A作AC⊥AB交直线l1于点C,若∠1=15°,则∠2=( )
A.105° B.115° C.100° D.95°
二、填空题(每小题3分,满分18分)
11.如图,∠1﹣∠2=72°.若l1∥l2,则∠ABC= °.
12.若是方程2x﹣y=2的一个解,则6a﹣3b+1=
13.已知:2x+3y﹣3=0,计算:4x 8y的值= .
14.在长方形ABCD中放入六个完全相同的小长方形,所标尺寸如图所示,则小长方形的宽CE为 cm.
15.某方程组的解为,则方程组的解是 .
16.关于x,y的方程组,满足x、y和等于3,则m= .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(一)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)化简:.
(2)解方程:.
18.解方程组:
(1); (2).
19.先化简,再求值:
(1)(x+1)2+(x+2)(x﹣3),其中.
(2)已知2a2+3a﹣4=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
20.如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,已知∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2:∠3=1:4,求∠BOF的度数.
21.某校组织七年级350名学生去研学,已知1辆A型车和2辆B型车可以载学生110人;3辆A型车和1辆B型车可以载学生130人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好送完学生,并且租车费用最少?
22.已知,关于x的分式方程1.
(1)当a=2,b=1时,求分式方程的解;
(2)当a=1时,求b为何值时分式方程1无解;
(3)若a=3b,且a、b为正整数,当分式方程1的解为整数时,求b的值.
23.我们把形如(m,n不为零),且两个解分别为x1=m,x2=n的方程称为“十字分式方程”.
例如为十字分式方程,可化为,∴x1=2,x2=3;
再如为十字分式方程,可化为,∴x1=﹣1,x2=﹣7.应用上面的结论解答下列问题:
(1)若为十字分式方程,则x1= ,x2= .
(2)若十字分式方程的两个解分别为x1=a,x2=b,求的值.
(3)若关于x的十字分式方程的两个解分别为x1,x2(k>2,x1>x2),求的值.
24.某段铁路两旁安置了A,D两座可旋转探照灯.已知PQ∥CN,A,B为PQ上两点,连接AC,∠C=20°,AD平分∠CAB交CN于点D,E为AD上一点,连接BE.
(1)求∠EAP= .
(2)如图,G为CN上一点,连接AG.当,∠2=3∠1时,试说明:AC∥BE;
(3)探照灯A、D照出的光线在铁路所在平面旋转,探照灯射出的光线AC以每秒5度的速度逆时针转动,探照灯D射出的光线DN以每秒15度的速度逆时针转动,DN转至射线DC后立即以相同速度回转,若它们同时开始转动,设转动时间为t秒,当DN回到出发时的位置时同时停止转动,则在转动过程中,当AC与DN互相平行或垂直时,请直接写出此时t的值.
25.把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.我们在学习“从面积到乘法公式”时,曾用两种不同的方法计算同一个图形的面积,探索了完全平方公式:(a+b)2=a2+2ab+b2(如图1).
(1)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
拓展应用:根据(1)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
(2)若,且x>y,求x﹣y的值;
(3)若(2025﹣m)2+(m﹣2024)2=7,求(2025﹣m)(m﹣2024)的值;
(4)如图3,在△BCE中,∠BCE=90°,CE=8,点M在边BC上,CM=3,在边CE上取一点Q,使BM=EQ,分别以BC,CQ为边在△BCE外部作正方形ABCD和正方形COPQ,连接BQ,若△BCQ的面积等于,设BM=x(x>0),求正方形ABCD和正方形COPQ的面积和.
参考答案
一、选择题
1—10:CBDDD CADAB
二、填空题
11.【解答】解:延长AB交直线l2于点F,设BC与直线l2交于点G,
∵l1∥l2,
∴∠2=∠AFG,
∵∠1是△BFG的一个外角,
∴∠FBG=∠1﹣∠AFG=∠1﹣∠2,
∵∠1﹣∠2=72°,
∴∠FBG=72°,
∴∠ABG=180°﹣∠FBG=108°,
故答案为:108.
12.【解答】解:把代入方程2x﹣y=2得:2a﹣b=2,
∴6a﹣3b+1
=3(2a﹣b)+1
=3×2+1
=6+1
=7,
故答案为:7.
13.【解答】解:∵2x+3y﹣3=0,
∴2x+3y=3,
∴4x 8y=22x 23y=22x+3y=23=8,
故答案为:8.
14.【解答】解:设小长方形的长为x cm,宽为y cm,
则AD=x+3y,AB=x+y=5+2y,
即x﹣y=5,
根据题意,得:,
解得:,
即CE=2cm,
故答案为:2.
15.【解答】解:将方程组变形为,
∵方程组的解为,
∴方程组的解为,即,
故答案为:.
16.【解答】解:,
由①﹣②得:x+2y=2③,
由x、y和等于3得到x+y=3,
联立③、④得方程组:,
解之得:,
把代入①得:3×4+5×(﹣1)=m+2,
解得m=5.
故答案为:5.
三、解答题
17.【解答】解:(1)原式
;
(2),
3(x﹣1)+3x=x+5,
3x﹣3+3x=x+5,
5x=8,
,
经检验:是方程的解.
18.【解答】解:(1),
把①代入②得:y=2(3y﹣2)﹣y,
解得:y=1,
∴x=3y﹣2=1,
故方程组的解为;
(2),
①×3﹣②×2得:﹣5y=﹣1,
解得:,
把代入①得:,
解得:,
故方程组的解为.
19.【解答】解:(1)(x+1)2+(x+2)(x﹣3)
=x2+2x+1+x2﹣x﹣6
=2x2+x﹣5;
(2)∵2a2+3a﹣4=0,
∴2a2+3a=4,
∴3a(2a+1)﹣(2a+1)(2a﹣1)
=6a2+3a﹣(4a2﹣1)
=6a2+3a﹣4a2+1
=2a2+3a+1
=4+1
=5.
20.【解答】(1)证明:∵OA,OB分别平分∠COE和∠DOE,
∴∠AOE∠COE,∠BOEDOE,
∴∠AOB=∠AOE+∠BOE(∠COE+∠DOE)=90°,
∴∠AOC+∠2=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD.
(2)解:设∠2=x,则∠3=4x,
∵OB分别平分∠DOE,
∴∠BOE=∠2=x,
∵∠3+∠2+∠BOE=180°,
∴4x+x+x=180°,
∴x=30°,
∴∠BOF=∠3+∠2=5x=150°.
21.【解答】解:(1)设每辆A型车可载学生x人,每辆B型车可载学生y人.
根据题意,得,
解得,
∴每辆A型车可载学生30人,每辆B型车可载学生40人.
(2)设租用A型车a辆,则租用B型车辆.
根据题意,租车费用W=1000a+1200100a+10500,
∵100>0,
∴W随a的减小而减小,
∵a≥0(a为整数),且为非负整数,
∴当a=1时,8,W取最小值,
∴租用A型车1辆,租用B型车8辆使得恰好送完学生,并且租车费用最少.
22.【解答】解:(1)把a=2,b=1代入分式方程 中,得,
方程两边同时乘以(2x+3)(x﹣5),
2(x﹣5)﹣(1﹣x)(2x+3)=(2x+3)(x﹣5),
2x2+3x﹣13=2x2﹣7x﹣15,
10x=﹣2,
x,
检验:把x 代入(2x+3)(x﹣5)≠0,所以原分式方程的解是x.
答:分式方程的解是x.
(2)把a=1代入分式方程 得,
方程两边同时乘以(2x+3)(x﹣5),
(x﹣5)﹣(b﹣x)(2x+3)=(2x+3)(x﹣5),
x﹣5+2x2+3x﹣2bx﹣3b=2x2﹣7x﹣15,
(11﹣2b)x=3b﹣10,
①当11﹣2b=0时,即,方程无解;
②当11﹣2b≠0时,,
时,分式方程无解,即,b不存在;
x=5时,分式方程无解,即,b=5.
综上所述,或b=5时,分式方程 无解.
(3)把a=3b代入分式方程 中,得:
方程两边同时乘以(2x+3)(x﹣5),
3b(x﹣5)+(x﹣b)(2x+3)=(2x+3)(x﹣5),
整理得:(10+b)x=18b﹣15,
∴,
∵,且b为正整数,x为整数,
∴10+b必为195的因数,10+b≥11,
∵195=3×5×13,
∴195的因数有1、3、5、13、15、39、65、195,
但1、3、5 小于11,不合题意,故10+b可以取13、15、39、65、195这五个数.
对应地,方程的解x为3、5、13、15、17,
由于x=5为分式方程的增根,故应舍去.
对应地,b只可以取3、29、55、185,
所以满足条件的b可取3、29、55、185这四个数.
23.【解答】解:(1)由题意,∵x4=1+3,
∴x1=1,x2=3.
故答案为:1;3.
(2)由题意,∵十字分式方程的两个解分别为x1=a,x2=b,
∴ab=﹣2,a+b=﹣3.
又∵11,
∴1.
(3)由题意,∵,
∴x﹣12025k﹣2025.
∴x﹣12024k﹣2025+k.
又∵关于x的十字分式方程的两个解分别为x1,x2(k>2,x1>x2),
∴x1﹣1=2024k﹣2025,x2﹣1=k.
∴x1=2024k﹣2024,x2=k+1.
∴2024.
24.【解答】解:(1)∵PQ∥CN,
∴∠PAC=∠C=20°,
∴∠CAB=180°﹣20°=160°,
∵AD平分∠CAB,
∴,
∴∠EAP=∠PAC+∠CAD=20°+80°=100°,
故答案为:100°;
(2)证明:∵,
∴∠ADC=3∠1,
∵∠2=3∠1,
∴∠2=∠ADC,
∵PQ∥CN,
∴∠EAP+∠ADC=180°,
∴∠ADC=180°﹣100°=80°,
∴∠2=80°,
∵∠PAC=20°,∠EAP=100°,
∴∠CAE=100°﹣20°=80°,
∴∠CAE=∠2,
∴AC∥BE;
(3)360°÷15°=24s,当AC∥DN时,则∠ACD=∠HDN,如图,
∵PB∥CH,
∴∠PAC=∠ACD,
∴∠PAC=∠HDN,
由题意得,∠PAC=20°+5t,∠HDN=15°t,
∴20°+5t=15°t,
∴t=2;
当AC⊥DN时,则∠CND=90°,如图,
∵PA∥CD,
∴∠ACD=∠PAC=20+5t,
∵∠NDH=15t,
∴∠NDC=180°﹣15°t,
∴20+5t+180°﹣15t=90°,
∴t=11;
当ND∥AC时,则∠NDC=∠ACH,如图,
由题意得,∠MDN=15t﹣180°,∠PAC=20°+5°t,
∴∠NDC=180°﹣∠MDN=360°﹣15°t,
∴20°+5°t=360°﹣15°t,
∴t=17;
当DN⊥AC时,∠DNC=90°,如图,
∵∠NDC=360°﹣15°t,
∴∠NDC+∠DCN=90°,
∵∠NCD=180°﹣(20°+5t),
∴360°﹣15t+180°﹣(20°+5t)=90°,
∴t=21.5;
综上,t的值为2或11或17或21.5.
25.【解答】解:(1)由图可知:大正方形的面积等于4个长方形的面积加上阴影正方形的面积,
∴(a+b)2=(a﹣b)2+4ab;
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)可得(x﹣y)2=(x+y)2﹣4xy,
∴(x﹣y)2=(x+y)2﹣4xy,
∵x>y,
∴x﹣y=3;
(3)由条件可知2ab=(a+b)2﹣(a2+b2),
∵(2025﹣m)2+(m﹣2024)2=7,
∴2(2025﹣m)(m﹣2024)
=(2025﹣m+m﹣2024)2﹣[(2025﹣m)2+(m﹣2024)2]
=1﹣7
=﹣6,
∴原式=﹣3;
(4)设BM=x,则BM=EQ=x,
∴CM=3,CE=8,
CQ=CE﹣EQ=8﹣x,BC=BM+CM=3+x,
∵,
∴(8﹣x)(3+x)=21,
令8﹣x=a,x+3=b,
∴a+b=11,ab=21,
∴正方形ABCD和正方形COPQ的面积和:
=a2+b2=(a+b)2﹣2ab=112﹣2×21=121﹣42=79.
21世纪教育网(www.21cnjy.com)
同课章节目录
