浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 338.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如图,三角形ABC沿射线BC方向平移到三角形DEF(点E在线段BC上),如果BC=10cm,EC=6cm,那么平移距离为( )
A.4cm B.6cm
C.10cm D.16cm
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.若分式的值为0,则x的值为( )
A.3 B.﹣3 C.±3 D.0
4.解分式方程时,去分母正确的是( )
A.2x﹣3=3x﹣1 B.2x﹣3(x﹣2)=3x﹣1
C.2x﹣3(x﹣2)=﹣3x﹣1 D.2x﹣3(x﹣2)=﹣3x+1
5.我国明代数学读本《算法统宗》中有一道题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”(注:这里1斤=16两,半斤=8两)其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两.若设客人为x人,银子为y两,可列方程组( )
A. B.
C. D.
6.如图,AB∥CD,EB⊥AB于点B,连接CE,若∠C=20°,则∠CEB=( )
A.120° B.115° C.100° D.110°
7.如图,已知AB∥CD∥EF,∠B=55°,∠C=135°,那么∠BEC等于( )
A.5° B.10° C.15° D.20°
8.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
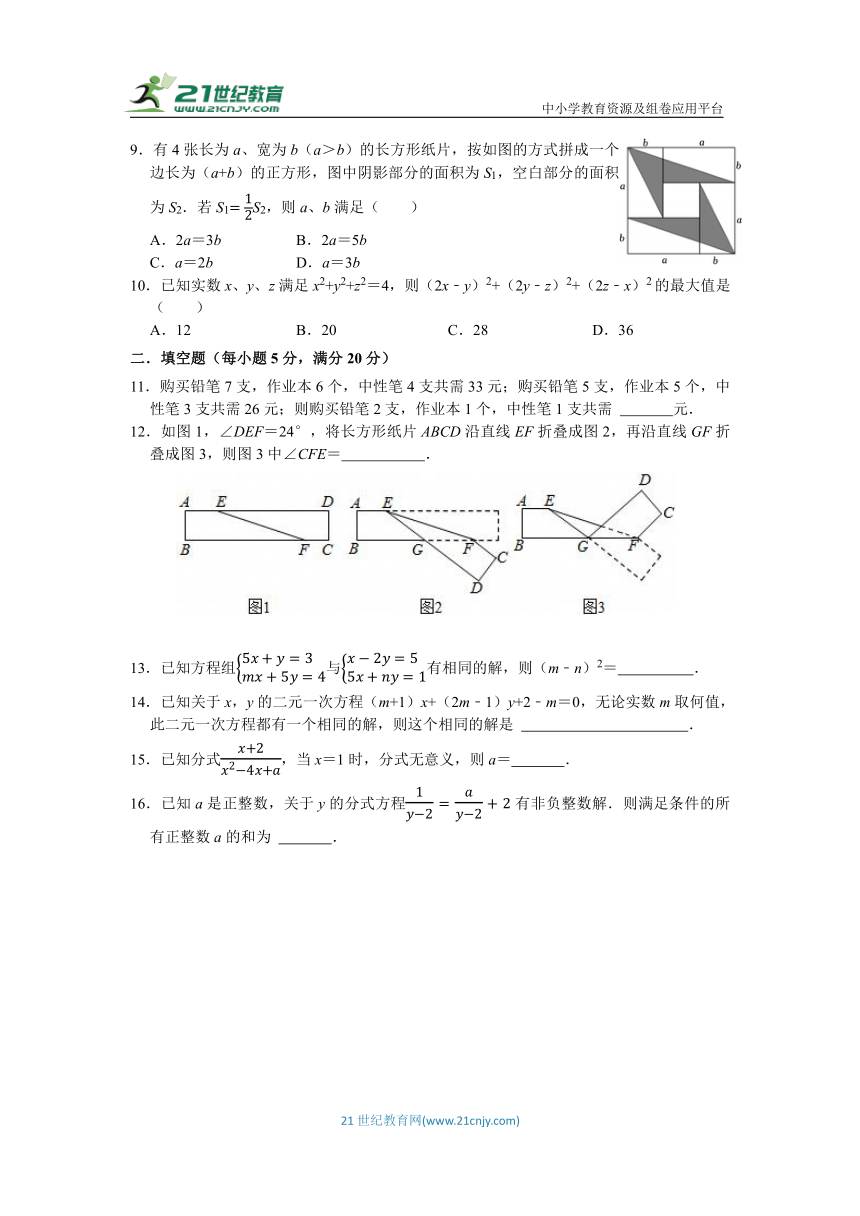
9.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1S2,则a、b满足( )
A.2a=3b B.2a=5b
C.a=2b D.a=3b
10.已知实数x、y、z满足x2+y2+z2=4,则(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是( )
A.12 B.20 C.28 D.36
二.填空题(每小题5分,满分20分)
11.购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
12.如图1,∠DEF=24°,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中∠CFE= .
13.已知方程组与有相同的解,则(m﹣n)2= .
14.已知关于x,y的二元一次方程(m+1)x+(2m﹣1)y+2﹣m=0,无论实数m取何值,此二元一次方程都有一个相同的解,则这个相同的解是 .
15.已知分式,当x=1时,分式无意义,则a= .
16.已知a是正整数,关于y的分式方程有非负整数解.则满足条件的所有正整数a的和为 .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.解方程组:
(1); (2).
19.先化简:,再从﹣2,﹣1,0,1,2中选择一个合适的数代入求值.
20.如图是10×8的正方形网格,每个小正方形的边长为1,其顶点称为格点.请按要求在图中画出格点三角形(顶点均在格点上)
(1)平移格点三角形ABC,画出平移后的格点三角形DEF(点A,B,C的对应点分别为点D,E,F);
(2)求三角形DEF的面积.
21.某大型超市花6000元购进甲、乙两种商品共220件,其中甲种商品每件25元,乙种商品每件30元.
(1)求甲、乙两种商品各购进多少件?
(2)A公司决定花1500元从该超市购买甲商品为员工发福利,B公司决定花1900元从该超市购买乙商品为员工发福利,其中甲商品的售价比乙商品的售价便宜8元,若两个公司购买的商品数量刚好一样,则超市能从这次销售中获利多少元?
22.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
23.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片多少张,B号卡片多少张,C号卡片多少张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2023)2+(x﹣2025)2=20,求x﹣2024的值.
24.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
25.定义:若分式A与分式B的差等于它们的积.即A﹣B=AB,则称分式B是分式A的“可存异分式”.如与.因为,.所以是的“可存异分式”.(1)填空:分式 分式的“可存异分式”.(填“是”或“不是”;)
(2)分式的“可存异分式”是 ;
(3)已知分式是分式A的“可存异分式”.
①求分式A的表达式;
②若整数x使得分式A的值是正整数,直接写出分式A的值;
(4)若关于x的分式是关于x的分式的“可存异分式”,求6n2+19n+534的值.
参考答案
一、选择题
1—10:ACADA ABBCC
二、填空题
11.【解答】解:设铅笔的单价是x元,作业本的单价是y元,中性笔的单价是z元.购买铅笔2支,作业本1本,中性笔1支共需a元.
则由题意得:
,
由①﹣②得2x+y+z=7,
于是:a=7,
故答案为:7.
12.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=24°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=156°,∠BFC=∠EFC﹣∠BFE=132°,
图3中,∠CFE=∠BFC﹣∠BFE=108°.
故答案为:108°.
13.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
14.【解答】解:方程整理得:mx+x+2my﹣y+2﹣m=0,
整理得:(x+2y﹣1)m+x﹣y+2=0,
由无论实数m取何值,此二元一次方程都有一个相同的解,
得到x+2y﹣1=0,x﹣y+2=0,
解得:,
故答案为:.
15.【解答】解:把x=1代入得:,
此时分式无意义,
∴a﹣3=0,
解得a=3.
故答案为:3.
16.【解答】解:,
1=a+2(y﹣2),
1=a+2y﹣4,
2y=4﹣a+1=5﹣a,
,
∵分式方程有非负整数解,
∴且,
∴a≤5且a≠1,
∵a是正整数,
∴a=5或3,
∴满足条件的所有正整数a的和为:5+3=8,
故答案为:8.
三、解答题
17.【解答】解:(1)原方程去分母得:2x﹣x(x+1)=(1﹣x)(x+1),
整理得:x=1,
检验:当x=1时,x(x+1)≠0,
故原方程的解为x=1;
(2)原方程去分母得:3(x﹣2)+2=﹣(x+2),
整理得:3x﹣4=﹣x﹣2,
解得:x=0.5,
检验:当x=0.5时,(x+2)(x﹣2)≠0,
18.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
19.【解答】解:原式
,
当x=2时,
原式.
20.【解答】解:(1)如图,三角形DEF即为所求,
(2)三角形DEF的面积为.
21.【解答】解:(1)设甲种商品购进x件,乙种商品购进y件,
由题意得:,
解得:,
答:甲种商品购进120件,乙种商品购进100件;
(2)设甲商品的售价为a元,则乙商品的售价为(a+8)元,
由题意得:,
解得:a=30,
经检验,a=30是原方程的解,且符合题意,
∴1500÷30=50(件),
∴50×(30﹣25)+50×(30+8﹣30)=650(元),
答:超市能从这次销售中获利650元.
22.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
23.【解答】解:(1)由题知,
图2的面积可表示为:(a+b)2,也可表示为:a2+b2+2ab,
所以(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+b2+2ab.
(2)因为(a+2b)(a+b)=a2+3ab+2b2,且A号卡片的面积为a2,B号卡片的面积为b2,C号卡片的面积为ab,
所以需要A号卡片1张,B号卡片2张,C号卡片3张.
(3)①由(1)知,
ab[(a+b)2﹣(a2+b2)].
②因为(x﹣2023)2+(x﹣2025)2=20,
所以(x﹣2024+1)2+(x﹣2024﹣1)2=20,
则(x﹣2024)2+2(x﹣2024)+1+(x﹣2024)2﹣2(x﹣2024)+1=20,
所以(x﹣2024)2=9,
则x﹣2024=±3.
24.【解答】解:(1)证明:∵AB∥CD,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴EF∥GH;
(2)如图2,过点N作NK∥CD,
∴KN∥CD∥AB,
∴∠KNE=∠4,∠6=∠7,
设∠4=x,∠7=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠5=∠4=x,∠6=∠8=∠7=y,
又∵AB∥CD,
∴∠EFD=180°﹣(∠4+∠5)=180°﹣2x,
又∵FM⊥GH,
∴∠EFM=90°,
∴180°﹣2x+2y=90°,
∴x﹣y=45°,
∴∠ENF=∠ENK﹣∠6=x﹣y=45°,
(3)
∵3∠FEN=4∠HFM,即3x=4×2y,
∴x,
∴x﹣yy=45°
∴y=27°,x=72°,
又∵EN和GQ是角平分线,
∴GQ⊥EN,
∴∠GQH=∠EGQ=180°﹣90°﹣72°=18°,
又∵∠MPN=∠FEN=x=72°,
∴,
故答案为.
25.【解答】解:(1)∵,.
∴,
,
∴,
∴分式不是分式的“可存异分式”;
故答案为:不是.
(2)设的“可存异分式”为N,则,
∴,
∴
.
故答案为:.
(3)①∵分式是分式A的“可存异分式”,
∴,
∴,
∴
;
②∵整数x使得分式A的值是正整数,,
∴x=1时,A=5,
x=3时,A=3,
x=﹣3时,A=1,
∴分式A的值是1,3,5;
(4)设关于x的分式的“可存异分式”为M,则:
,
∴
,
∵关于x的分式是关于x的分式的“可存异分式”,
∴,
整理得:,
解得:,
∴6n2+19n+534
=520.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如图,三角形ABC沿射线BC方向平移到三角形DEF(点E在线段BC上),如果BC=10cm,EC=6cm,那么平移距离为( )
A.4cm B.6cm
C.10cm D.16cm
2.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
3.若分式的值为0,则x的值为( )
A.3 B.﹣3 C.±3 D.0
4.解分式方程时,去分母正确的是( )
A.2x﹣3=3x﹣1 B.2x﹣3(x﹣2)=3x﹣1
C.2x﹣3(x﹣2)=﹣3x﹣1 D.2x﹣3(x﹣2)=﹣3x+1
5.我国明代数学读本《算法统宗》中有一道题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”(注:这里1斤=16两,半斤=8两)其题意为:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两.若设客人为x人,银子为y两,可列方程组( )
A. B.
C. D.
6.如图,AB∥CD,EB⊥AB于点B,连接CE,若∠C=20°,则∠CEB=( )
A.120° B.115° C.100° D.110°
7.如图,已知AB∥CD∥EF,∠B=55°,∠C=135°,那么∠BEC等于( )
A.5° B.10° C.15° D.20°
8.若a,b是正整数,且满足3a+3a+3a=3b×3b×3b,则下列a与b的关系正确的是( )
A.a=b B.a+1=3b C.a+1=b3 D.3a=b3
9.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1S2,则a、b满足( )
A.2a=3b B.2a=5b
C.a=2b D.a=3b
10.已知实数x、y、z满足x2+y2+z2=4,则(2x﹣y)2+(2y﹣z)2+(2z﹣x)2的最大值是( )
A.12 B.20 C.28 D.36
二.填空题(每小题5分,满分20分)
11.购买铅笔7支,作业本6个,中性笔4支共需33元;购买铅笔5支,作业本5个,中性笔3支共需26元;则购买铅笔2支,作业本1个,中性笔1支共需 元.
12.如图1,∠DEF=24°,将长方形纸片ABCD沿直线EF折叠成图2,再沿直线GF折叠成图3,则图3中∠CFE= .
13.已知方程组与有相同的解,则(m﹣n)2= .
14.已知关于x,y的二元一次方程(m+1)x+(2m﹣1)y+2﹣m=0,无论实数m取何值,此二元一次方程都有一个相同的解,则这个相同的解是 .
15.已知分式,当x=1时,分式无意义,则a= .
16.已知a是正整数,关于y的分式方程有非负整数解.则满足条件的所有正整数a的和为 .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解方程:
(1); (2).
18.解方程组:
(1); (2).
19.先化简:,再从﹣2,﹣1,0,1,2中选择一个合适的数代入求值.
20.如图是10×8的正方形网格,每个小正方形的边长为1,其顶点称为格点.请按要求在图中画出格点三角形(顶点均在格点上)
(1)平移格点三角形ABC,画出平移后的格点三角形DEF(点A,B,C的对应点分别为点D,E,F);
(2)求三角形DEF的面积.
21.某大型超市花6000元购进甲、乙两种商品共220件,其中甲种商品每件25元,乙种商品每件30元.
(1)求甲、乙两种商品各购进多少件?
(2)A公司决定花1500元从该超市购买甲商品为员工发福利,B公司决定花1900元从该超市购买乙商品为员工发福利,其中甲商品的售价比乙商品的售价便宜8元,若两个公司购买的商品数量刚好一样,则超市能从这次销售中获利多少元?
22.今年元旦期间某物流公司计划用两种车型运输新年物资,用2辆A型车和1辆B型车装满物资一次可运10吨:用1辆A型车和2辆B型车一次可运11吨.
(1)求每辆A型车和每辆B型车都装满物资一次可分别运多少吨.
(2)某物流公司现有31吨货物资,计划同时租用A型车a辆,B型车b辆,一次运完且恰好每辆车都装满.若A型车每辆需租金每次200元,B型车租金每次300元,求最少租车费用.
23.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b、宽为a的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系;
(2)若要拼出一个面积为(a+2b)(a+b)的矩形,则需要A号卡片多少张,B号卡片多少张,C号卡片多少张.
(3)根据(1)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x﹣2023)2+(x﹣2025)2=20,求x﹣2024的值.
24.已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
25.定义:若分式A与分式B的差等于它们的积.即A﹣B=AB,则称分式B是分式A的“可存异分式”.如与.因为,.所以是的“可存异分式”.(1)填空:分式 分式的“可存异分式”.(填“是”或“不是”;)
(2)分式的“可存异分式”是 ;
(3)已知分式是分式A的“可存异分式”.
①求分式A的表达式;
②若整数x使得分式A的值是正整数,直接写出分式A的值;
(4)若关于x的分式是关于x的分式的“可存异分式”,求6n2+19n+534的值.
参考答案
一、选择题
1—10:ACADA ABBCC
二、填空题
11.【解答】解:设铅笔的单价是x元,作业本的单价是y元,中性笔的单价是z元.购买铅笔2支,作业本1本,中性笔1支共需a元.
则由题意得:
,
由①﹣②得2x+y+z=7,
于是:a=7,
故答案为:7.
12.【解答】解:∵四边形ABCD为长方形,
∴AD∥BC,
∴∠BFE=∠DEF=24°.
由翻折的性质可知:
图2中,∠EFC=180°﹣∠BFE=156°,∠BFC=∠EFC﹣∠BFE=132°,
图3中,∠CFE=∠BFC﹣∠BFE=108°.
故答案为:108°.
13.【解答】解:∵方程组与有相同的解,
∴与有相同的解,
①×2+②得:x=1,
把x=1代入①得:y=﹣2,
把x=1,y=﹣2代入③得:m=14,
把x=1,y=﹣2代入④得:n=2,
∴(m﹣n)2=(14﹣2)2=122=144,
故答案为:144.
14.【解答】解:方程整理得:mx+x+2my﹣y+2﹣m=0,
整理得:(x+2y﹣1)m+x﹣y+2=0,
由无论实数m取何值,此二元一次方程都有一个相同的解,
得到x+2y﹣1=0,x﹣y+2=0,
解得:,
故答案为:.
15.【解答】解:把x=1代入得:,
此时分式无意义,
∴a﹣3=0,
解得a=3.
故答案为:3.
16.【解答】解:,
1=a+2(y﹣2),
1=a+2y﹣4,
2y=4﹣a+1=5﹣a,
,
∵分式方程有非负整数解,
∴且,
∴a≤5且a≠1,
∵a是正整数,
∴a=5或3,
∴满足条件的所有正整数a的和为:5+3=8,
故答案为:8.
三、解答题
17.【解答】解:(1)原方程去分母得:2x﹣x(x+1)=(1﹣x)(x+1),
整理得:x=1,
检验:当x=1时,x(x+1)≠0,
故原方程的解为x=1;
(2)原方程去分母得:3(x﹣2)+2=﹣(x+2),
整理得:3x﹣4=﹣x﹣2,
解得:x=0.5,
检验:当x=0.5时,(x+2)(x﹣2)≠0,
18.【解答】解:(1),
①+②得5x=10,
解得:x=2,
将x=2代入①得8+2y=7,
解得:,
∴原方程组的解是;
(2),
由①得:3x﹣4x+4y=2,
整理得:x=4y﹣2 ③,
把③代入②得:2(4y﹣2)﹣3y=1,
解得:y=1
将y=1代入②得2x﹣3=1,
解得:x=2,
∴原方程组的解是.
19.【解答】解:原式
,
当x=2时,
原式.
20.【解答】解:(1)如图,三角形DEF即为所求,
(2)三角形DEF的面积为.
21.【解答】解:(1)设甲种商品购进x件,乙种商品购进y件,
由题意得:,
解得:,
答:甲种商品购进120件,乙种商品购进100件;
(2)设甲商品的售价为a元,则乙商品的售价为(a+8)元,
由题意得:,
解得:a=30,
经检验,a=30是原方程的解,且符合题意,
∴1500÷30=50(件),
∴50×(30﹣25)+50×(30+8﹣30)=650(元),
答:超市能从这次销售中获利650元.
22.【解答】解:(1)设每辆A型车装满物资一次可运x吨,每辆B型车装满物资一次可运y吨,
依题意得:,
解得:,
答:每辆A型车装满物资一次可运3吨,每辆B型车装满物资一次可运4吨;
(2)依题意得:3a+4b=31,
∵a,b均为正整数,
∴或或,
∴该物流公司共有3种租车方案,
方案1:租用9辆A型车,1辆B型车,所需租金300×9+200×1=2900(元);
方案2:租用5辆A型车,4辆B型车,所需租金为300×5+200×4=2300(元);
方案3:租用1辆A型车,7辆B型车,所需租金为300×1+200×7=1700(元);
∵2900>2300>1700,
∴最省钱的租车方案为租用1辆A型车,7辆B型车,最少租车费为1700元.
23.【解答】解:(1)由题知,
图2的面积可表示为:(a+b)2,也可表示为:a2+b2+2ab,
所以(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+b2+2ab.
(2)因为(a+2b)(a+b)=a2+3ab+2b2,且A号卡片的面积为a2,B号卡片的面积为b2,C号卡片的面积为ab,
所以需要A号卡片1张,B号卡片2张,C号卡片3张.
(3)①由(1)知,
ab[(a+b)2﹣(a2+b2)].
②因为(x﹣2023)2+(x﹣2025)2=20,
所以(x﹣2024+1)2+(x﹣2024﹣1)2=20,
则(x﹣2024)2+2(x﹣2024)+1+(x﹣2024)2﹣2(x﹣2024)+1=20,
所以(x﹣2024)2=9,
则x﹣2024=±3.
24.【解答】解:(1)证明:∵AB∥CD,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴EF∥GH;
(2)如图2,过点N作NK∥CD,
∴KN∥CD∥AB,
∴∠KNE=∠4,∠6=∠7,
设∠4=x,∠7=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠5=∠4=x,∠6=∠8=∠7=y,
又∵AB∥CD,
∴∠EFD=180°﹣(∠4+∠5)=180°﹣2x,
又∵FM⊥GH,
∴∠EFM=90°,
∴180°﹣2x+2y=90°,
∴x﹣y=45°,
∴∠ENF=∠ENK﹣∠6=x﹣y=45°,
(3)
∵3∠FEN=4∠HFM,即3x=4×2y,
∴x,
∴x﹣yy=45°
∴y=27°,x=72°,
又∵EN和GQ是角平分线,
∴GQ⊥EN,
∴∠GQH=∠EGQ=180°﹣90°﹣72°=18°,
又∵∠MPN=∠FEN=x=72°,
∴,
故答案为.
25.【解答】解:(1)∵,.
∴,
,
∴,
∴分式不是分式的“可存异分式”;
故答案为:不是.
(2)设的“可存异分式”为N,则,
∴,
∴
.
故答案为:.
(3)①∵分式是分式A的“可存异分式”,
∴,
∴,
∴
;
②∵整数x使得分式A的值是正整数,,
∴x=1时,A=5,
x=3时,A=3,
x=﹣3时,A=1,
∴分式A的值是1,3,5;
(4)设关于x的分式的“可存异分式”为M,则:
,
∴
,
∵关于x的分式是关于x的分式的“可存异分式”,
∴,
整理得:,
解得:,
∴6n2+19n+534
=520.
21世纪教育网(www.21cnjy.com)
同课章节目录
