浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷(含答案)
文档属性
| 名称 | 浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 15:50:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
2.下列各式是最简分式的是( )
A. B. C. D.
3.如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
4.若实数a,b满足a2+b2=8,ab=4,则a+b的值为( )
A. B.4 C. D.±4
5.若a是大于1的正整数,且满足,则n的值是( )
A.5 B.6 C.7 D.8
6.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
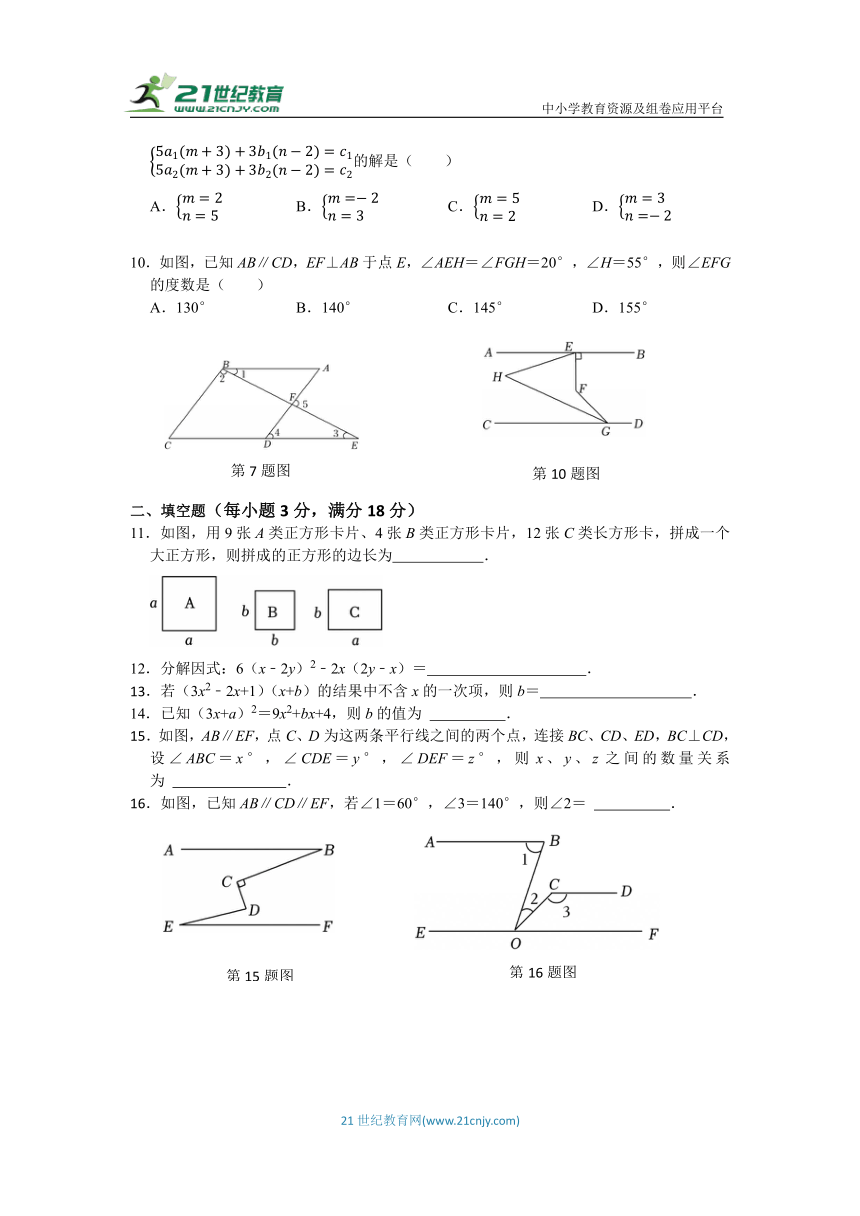
7.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
8.若关于x的分式方程无解,则a的值为( )
A.﹣1 B. C.﹣1或0 D.﹣1或
9.已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是( )
A. B. C. D.
10.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
二、填空题(每小题3分,满分18分)
11.如图,用9张A类正方形卡片、4张B类正方形卡片,12张C类长方形卡,拼成一个大正方形,则拼成的正方形的边长为 .
12.分解因式:6(x﹣2y)2﹣2x(2y﹣x)= .
13.若(3x2﹣2x+1)(x+b)的结果中不含x的一次项,则b= .
14.已知(3x+a)2=9x2+bx+4,则b的值为 .
15.如图,AB∥EF,点C、D为这两条平行线之间的两个点,连接BC、CD、ED,BC⊥CD,设∠ABC=x°,∠CDE=y°,∠DEF=z°,则x、y、z之间的数量关系为 .
16.如图,已知AB∥CD∥EF,若∠1=60°,∠3=140°,则∠2= .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1); (2).
18.计算:.
19.先化简,再求值:[(x﹣2y)2+(x+2y)(x﹣2y)]÷2x,其中x=﹣3,y=5.
20.在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
21.某山区有23名中、小学生因贫困失学需要资助,已知资助一名中学生的学习费用为a元,资助一名小学生的学习费用为b元.某校学生积极捐助,初中各年级学生捐款数额与用其恰好资助贫困中学生和小学生人数的部分情况如下表:
年级 捐款数额(元) 资助贫困中学生人数(名) 资助贫困小学生人数(名)
初一年级 4000 2 4
初二年级 4200 3 3
初三年级 7400
(1)求a、b的值;
(2)初三年级学生的捐款恰好解决了其余贫困中小学生的学习费用,求初三年级学生的捐款可资助的贫困中、小学生人数分别为多少.
22.某大型超市花6000元购进甲、乙两种商品共220件,其中甲种商品每件25元,乙种商品每件30元.
(1)求甲、乙两种商品各购进多少件?
(2)A公司决定花1500元从该超市购买甲商品为员工发福利,B公司决定花1900元从该超市购买乙商品为员工发福利,其中甲商品的售价比乙商品的售价便宜8元,若两个公司购买的商品数量刚好一样,则超市能从这次销售中获利多少元?
23.如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠DEF=∠B,DE∥BC.
(1)求证:∠BDC=∠DFE;
(2)若DE平分∠ADC,∠BDC=2∠B,求∠BDC的度数.
24.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
25.定义:关于x,y的二元一次方程ax+by=c(其中a≠b≠c)中的常数项c与未知数系数a,b之一互换,得到的方程叫“交换系数方程”,例如:ax+by=c的“交换系数方程”为cx+by=a或ax+cy=b.
(1)方程3x+2y=4的“交换系数方程”为 ;
(2)已知关于x,y的二元一次方程ax+by=c的系数满足a+b+c=0,且ax+by=c与它的“交换系数方程”组成的方程组的解恰好是关于x,y的二元一次方程mx+ny=p的一个解,求m+p+n+2024的值;
(3)已知m,n,t都是整数,并且(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,求9m﹣n的值.
参考答案
一、选择题
1—10:CCBDC DDDBC
二、填空题
11.【解答】解:根据题意用9张A类正方形卡片、4张B类正方形卡片,12张C类长方形卡,
可拼成的大正方形的面积为:9a2+12ab+4b2=(3a+2b)2,
故拼成的大正方形边长是:3a+2b,
故答案为:3a+2b.
12.【解答】解:原式=6(x﹣2y)2+2x(x﹣2y)
=(x﹣2y)[6(x﹣2y)+2x]
=4(x﹣2y)(2x﹣3y).
故答案为:4(x﹣2y)(2x﹣3y).
13.【解答】解:∵多项式(3x2﹣2x+1)(x+b)=3x3+(3b﹣2)x2+(1﹣2b)x+b不含x的一次项,
∴1﹣2b=0,
解得b.
故答案为:.
14.【解答】解:(3x+a)2=9x2+6ax+a2,
∵9x2+6ax+a2=9x2+bx+4,
∴a2=4,6a=b,
∴a=±2,b=±12.
故答案为:±12.
15.【解答】解:如图所示,过点C,D分别作CG∥AB,DH∥AB,
∴AB∥CG∥DH∥EF,
∴∠ABC=∠BCG=x°,∠GCD=∠CDH,∠HDE=∠DEF=z°,
∵∠CDH+∠HDE=∠CDE=y°,∠GCD=∠BCD﹣∠BCG=90°﹣x°,
∴90°﹣x°+z°=y°,
∴x°+y°﹣z°=90°,
所以x、y、z之间的数量关系为x°+y°﹣z°=90°,
故答案为:x+y﹣z=90.
16.【解答】解:∵AB∥EF,
∴∠BOF=∠1=60°,
∵CD∥EF,
∴∠COF=180°﹣∠3=180°﹣140°=40°,
∴∠2=∠BOF﹣∠COF=60°﹣40°=20°,
故答案为:20°.
三、解答题
17.【解答】解:(1),
把①代入②,得x+x﹣2=6,
解得:x=4,
把x=4代入①,得y=4﹣2=2,
∴方程组的解为;
(2),
②×2,得10x+4y=20③,
③﹣①,得7x=14,
解得:x=2,
把x=2代入①,得3×2+4y=6,
解得:y=0,
∴方程组的解为.
18.【解答】解:
=﹣1+4+1﹣2
=2.
19.【解答】解:[(x﹣2y)2+(x+2y)(x﹣2y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2)÷2x
=(2x2﹣4xy)÷2x
=2x2÷2x﹣4xy÷2x
=x﹣2y,
当x=﹣3,y=5时,原式=﹣3﹣2×5=﹣13.
20.【解答】解:(1)将代入②得b=﹣10,
将代入①得a=﹣1;
(2)原方程组为,
①×2﹣②得:﹣6x=32,
解得:x,
①×4+②得:30y=58,
解得:y,
即原方程组的解为:.
21.【解答】解:(1)依题意得,
解得.
答:a的值为800,b的值为600;
(2)设初三年级学生的捐款可资助贫困中学生x人,小学生y人,
依题意得,
解得.
答:初三年级学生的捐款可资助贫困中学生4人,小学生7人.
22.【解答】解:(1)设甲种商品购进x件,乙种商品购进y件,
由题意得:,
解得:,
答:甲种商品购进120件,乙种商品购进100件;
(2)设甲商品的售价为a元,则乙商品的售价为(a+8)元,
由题意得:,
解得:a=30,
经检验,a=30是原方程的解,且符合题意,
∴1500÷30=50(件),
∴50×(30﹣25)+50×(30+8﹣30)=650(元),
答:超市能从这次销售中获利650元.
23.【解答】(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠DEF,
∴AD∥EF,
∴∠BDC=∠DFE;
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵∠ADE=∠B,
∴∠ADC=2∠B,
∵∠BDC=2∠B,∠BDC+∠ADC=180°,
∴2∠B+2∠B=180°,
∴∠B=45°,
∴∠BDC=2∠B=90°.
24.【解答】(1)证明:∵AB∥CD,
∴∠FEG=∠EFP,
∵EF∥GH,
∴∠EFP=∠PHG,
∴∠PHG=∠FEG;
(2)解:∵AB∥CD,
∴∠EPF=∠PEA,
∵EP平分∠AEF,
∴∠AEP∠AEF,
∴∠EPF∠AEF,
∵∠AEF+∠FEG=180°,
∴∠EPF(180°﹣∠FEG),
由(1)知∠PHG=∠FEG;
∴∠EPF(180°﹣∠PHG),
∵∠EPF:∠PHG=1:3,
可设∠EPF=x,则∠PHG=3x,
则x(180°﹣3x),
解得x=36°,
∴∠PHG=108°,
∵EF∥GH,
∴∠EFD+∠PHG=180°,
∴∠EFD=72°;
(3)解:∠PEM+∠EMF=90°;理由如下:
设∠EMF=α,∠EMG=β,则∠HFM=∠HMF=α+β,
∵EF∥GH,
∴∠EFM+∠HMF=180°,∠FEM=β,
∴∠EFM=180°﹣(α+β),
∴∠EFH=∠EFM﹣∠HFM=180°﹣2(α+β),
∵AB∥CD,
∴∠AEF=∠EFH=180°﹣2(α+β),
∵EP平分∠AEF,
∴∠PEF∠AEF=90°﹣α﹣β,
∴∠PEM=∠PEF+FEM=90°﹣α﹣β+β=90°﹣α,
∵∠EMF=α,
∴∠PEM=90°﹣∠EMF,
∴∠PEM+∠EMF=90°.
25.【解答】解:(1)根据“交换系数方程”的定义可知方程“3x+2y=4”的交换系数方程为4x+2y=3或3x+4y=2.
故答案为:4x+2y=3或3x+4y=2.
(2)当ax+by=c的“交换系数方程”为ax+cy=b时,
联立,解得:,
∵a+b+c=0,
∴b+c=﹣a,
∴,
当ax+by=c的“交换系数方程”为cx+by=a时,
联立,解得:,
由条件可知b+c=﹣a,
∴.
综上:ax+by=c与它的“交换系数方 程”组成的方程组的解为.
把代入方程mx+ny=p得:﹣m﹣n=p,即p+m+n=0,
∴m+p+n+2024=0+2024=2024.
(3)由条件可知或,
①当时,整理得:,解得:;
;
②当时,解得:,
∴.
综上:9m﹣n=3.
21世纪教育网(www.21cnjy.com)
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷
满分:120分 时间:120分钟 范围:第一章相交线与平行线到第五章分式
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.石墨烯目前是世界上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )
A.0.34×10﹣9 B.3.4×10﹣9 C.3.4×10﹣10 D.3.4×10﹣11
2.下列各式是最简分式的是( )
A. B. C. D.
3.如果分式中的x,y都扩大为原来的2倍,那么分式的值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的4倍 D.缩小为原来的倍
4.若实数a,b满足a2+b2=8,ab=4,则a+b的值为( )
A. B.4 C. D.±4
5.若a是大于1的正整数,且满足,则n的值是( )
A.5 B.6 C.7 D.8
6.解方程组时,一学生把c看错而得到,而正确的解是,那么a+b+c的值为( )
A.4 B.5 C.6 D.7
7.如图,点E在CD的延长线上,BE与AD交于点F,下列条件能判断BC∥AD的是( )
A.∠1=∠3 B.∠A+∠CDA=180°
C.∠4=∠A D.∠2+∠5=180°
8.若关于x的分式方程无解,则a的值为( )
A.﹣1 B. C.﹣1或0 D.﹣1或
9.已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是( )
A. B. C. D.
10.如图,已知AB∥CD,EF⊥AB于点E,∠AEH=∠FGH=20°,∠H=55°,则∠EFG的度数是( )
A.130° B.140° C.145° D.155°
二、填空题(每小题3分,满分18分)
11.如图,用9张A类正方形卡片、4张B类正方形卡片,12张C类长方形卡,拼成一个大正方形,则拼成的正方形的边长为 .
12.分解因式:6(x﹣2y)2﹣2x(2y﹣x)= .
13.若(3x2﹣2x+1)(x+b)的结果中不含x的一次项,则b= .
14.已知(3x+a)2=9x2+bx+4,则b的值为 .
15.如图,AB∥EF,点C、D为这两条平行线之间的两个点,连接BC、CD、ED,BC⊥CD,设∠ABC=x°,∠CDE=y°,∠DEF=z°,则x、y、z之间的数量关系为 .
16.如图,已知AB∥CD∥EF,若∠1=60°,∠3=140°,则∠2= .
浙教版2024—2025学年七年级下学期数学第三次月考模拟试卷B卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列方程组:
(1); (2).
18.计算:.
19.先化简,再求值:[(x﹣2y)2+(x+2y)(x﹣2y)]÷2x,其中x=﹣3,y=5.
20.在解方程组时,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得到的解是.
(1)求原方程组中a、b的值各是多少?
(2)求出原方程组中的正确解.
21.某山区有23名中、小学生因贫困失学需要资助,已知资助一名中学生的学习费用为a元,资助一名小学生的学习费用为b元.某校学生积极捐助,初中各年级学生捐款数额与用其恰好资助贫困中学生和小学生人数的部分情况如下表:
年级 捐款数额(元) 资助贫困中学生人数(名) 资助贫困小学生人数(名)
初一年级 4000 2 4
初二年级 4200 3 3
初三年级 7400
(1)求a、b的值;
(2)初三年级学生的捐款恰好解决了其余贫困中小学生的学习费用,求初三年级学生的捐款可资助的贫困中、小学生人数分别为多少.
22.某大型超市花6000元购进甲、乙两种商品共220件,其中甲种商品每件25元,乙种商品每件30元.
(1)求甲、乙两种商品各购进多少件?
(2)A公司决定花1500元从该超市购买甲商品为员工发福利,B公司决定花1900元从该超市购买乙商品为员工发福利,其中甲商品的售价比乙商品的售价便宜8元,若两个公司购买的商品数量刚好一样,则超市能从这次销售中获利多少元?
23.如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠DEF=∠B,DE∥BC.
(1)求证:∠BDC=∠DFE;
(2)若DE平分∠ADC,∠BDC=2∠B,求∠BDC的度数.
24.已知直线AB∥CD,点E,G为直线AB上不重合的两个点,EF∥GH,分别交直线CD于点F,H,EP平分∠AEF交CD于点P.
(1)如图1,试说明:∠PHG=∠FEG;
(2)如图1,若∠EPF:∠PHG=1:3,求∠EFD的大小.
(3)如图2,点M为线段GH延长线上一点,连结EM,FM.若∠HFM=∠HMF,试探索∠PEM与∠EMF的数量关系,并说明理由.
25.定义:关于x,y的二元一次方程ax+by=c(其中a≠b≠c)中的常数项c与未知数系数a,b之一互换,得到的方程叫“交换系数方程”,例如:ax+by=c的“交换系数方程”为cx+by=a或ax+cy=b.
(1)方程3x+2y=4的“交换系数方程”为 ;
(2)已知关于x,y的二元一次方程ax+by=c的系数满足a+b+c=0,且ax+by=c与它的“交换系数方程”组成的方程组的解恰好是关于x,y的二元一次方程mx+ny=p的一个解,求m+p+n+2024的值;
(3)已知m,n,t都是整数,并且(10m﹣t)x+2023y=m+t是关于x,y的二元一次方程(1+n)x+2023y=2m+2的“交换系数方程”,求9m﹣n的值.
参考答案
一、选择题
1—10:CCBDC DDDBC
二、填空题
11.【解答】解:根据题意用9张A类正方形卡片、4张B类正方形卡片,12张C类长方形卡,
可拼成的大正方形的面积为:9a2+12ab+4b2=(3a+2b)2,
故拼成的大正方形边长是:3a+2b,
故答案为:3a+2b.
12.【解答】解:原式=6(x﹣2y)2+2x(x﹣2y)
=(x﹣2y)[6(x﹣2y)+2x]
=4(x﹣2y)(2x﹣3y).
故答案为:4(x﹣2y)(2x﹣3y).
13.【解答】解:∵多项式(3x2﹣2x+1)(x+b)=3x3+(3b﹣2)x2+(1﹣2b)x+b不含x的一次项,
∴1﹣2b=0,
解得b.
故答案为:.
14.【解答】解:(3x+a)2=9x2+6ax+a2,
∵9x2+6ax+a2=9x2+bx+4,
∴a2=4,6a=b,
∴a=±2,b=±12.
故答案为:±12.
15.【解答】解:如图所示,过点C,D分别作CG∥AB,DH∥AB,
∴AB∥CG∥DH∥EF,
∴∠ABC=∠BCG=x°,∠GCD=∠CDH,∠HDE=∠DEF=z°,
∵∠CDH+∠HDE=∠CDE=y°,∠GCD=∠BCD﹣∠BCG=90°﹣x°,
∴90°﹣x°+z°=y°,
∴x°+y°﹣z°=90°,
所以x、y、z之间的数量关系为x°+y°﹣z°=90°,
故答案为:x+y﹣z=90.
16.【解答】解:∵AB∥EF,
∴∠BOF=∠1=60°,
∵CD∥EF,
∴∠COF=180°﹣∠3=180°﹣140°=40°,
∴∠2=∠BOF﹣∠COF=60°﹣40°=20°,
故答案为:20°.
三、解答题
17.【解答】解:(1),
把①代入②,得x+x﹣2=6,
解得:x=4,
把x=4代入①,得y=4﹣2=2,
∴方程组的解为;
(2),
②×2,得10x+4y=20③,
③﹣①,得7x=14,
解得:x=2,
把x=2代入①,得3×2+4y=6,
解得:y=0,
∴方程组的解为.
18.【解答】解:
=﹣1+4+1﹣2
=2.
19.【解答】解:[(x﹣2y)2+(x+2y)(x﹣2y)]÷2x
=(x2﹣4xy+4y2+x2﹣4y2)÷2x
=(2x2﹣4xy)÷2x
=2x2÷2x﹣4xy÷2x
=x﹣2y,
当x=﹣3,y=5时,原式=﹣3﹣2×5=﹣13.
20.【解答】解:(1)将代入②得b=﹣10,
将代入①得a=﹣1;
(2)原方程组为,
①×2﹣②得:﹣6x=32,
解得:x,
①×4+②得:30y=58,
解得:y,
即原方程组的解为:.
21.【解答】解:(1)依题意得,
解得.
答:a的值为800,b的值为600;
(2)设初三年级学生的捐款可资助贫困中学生x人,小学生y人,
依题意得,
解得.
答:初三年级学生的捐款可资助贫困中学生4人,小学生7人.
22.【解答】解:(1)设甲种商品购进x件,乙种商品购进y件,
由题意得:,
解得:,
答:甲种商品购进120件,乙种商品购进100件;
(2)设甲商品的售价为a元,则乙商品的售价为(a+8)元,
由题意得:,
解得:a=30,
经检验,a=30是原方程的解,且符合题意,
∴1500÷30=50(件),
∴50×(30﹣25)+50×(30+8﹣30)=650(元),
答:超市能从这次销售中获利650元.
23.【解答】(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠DEF,
∴AD∥EF,
∴∠BDC=∠DFE;
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵∠ADE=∠B,
∴∠ADC=2∠B,
∵∠BDC=2∠B,∠BDC+∠ADC=180°,
∴2∠B+2∠B=180°,
∴∠B=45°,
∴∠BDC=2∠B=90°.
24.【解答】(1)证明:∵AB∥CD,
∴∠FEG=∠EFP,
∵EF∥GH,
∴∠EFP=∠PHG,
∴∠PHG=∠FEG;
(2)解:∵AB∥CD,
∴∠EPF=∠PEA,
∵EP平分∠AEF,
∴∠AEP∠AEF,
∴∠EPF∠AEF,
∵∠AEF+∠FEG=180°,
∴∠EPF(180°﹣∠FEG),
由(1)知∠PHG=∠FEG;
∴∠EPF(180°﹣∠PHG),
∵∠EPF:∠PHG=1:3,
可设∠EPF=x,则∠PHG=3x,
则x(180°﹣3x),
解得x=36°,
∴∠PHG=108°,
∵EF∥GH,
∴∠EFD+∠PHG=180°,
∴∠EFD=72°;
(3)解:∠PEM+∠EMF=90°;理由如下:
设∠EMF=α,∠EMG=β,则∠HFM=∠HMF=α+β,
∵EF∥GH,
∴∠EFM+∠HMF=180°,∠FEM=β,
∴∠EFM=180°﹣(α+β),
∴∠EFH=∠EFM﹣∠HFM=180°﹣2(α+β),
∵AB∥CD,
∴∠AEF=∠EFH=180°﹣2(α+β),
∵EP平分∠AEF,
∴∠PEF∠AEF=90°﹣α﹣β,
∴∠PEM=∠PEF+FEM=90°﹣α﹣β+β=90°﹣α,
∵∠EMF=α,
∴∠PEM=90°﹣∠EMF,
∴∠PEM+∠EMF=90°.
25.【解答】解:(1)根据“交换系数方程”的定义可知方程“3x+2y=4”的交换系数方程为4x+2y=3或3x+4y=2.
故答案为:4x+2y=3或3x+4y=2.
(2)当ax+by=c的“交换系数方程”为ax+cy=b时,
联立,解得:,
∵a+b+c=0,
∴b+c=﹣a,
∴,
当ax+by=c的“交换系数方程”为cx+by=a时,
联立,解得:,
由条件可知b+c=﹣a,
∴.
综上:ax+by=c与它的“交换系数方 程”组成的方程组的解为.
把代入方程mx+ny=p得:﹣m﹣n=p,即p+m+n=0,
∴m+p+n+2024=0+2024=2024.
(3)由条件可知或,
①当时,整理得:,解得:;
;
②当时,解得:,
∴.
综上:9m﹣n=3.
21世纪教育网(www.21cnjy.com)
同课章节目录
