浙江省宁波市艺术实验2024-2025学年第二学期八年级4月期中数学评估试卷(含答案)
文档属性
| 名称 | 浙江省宁波市艺术实验2024-2025学年第二学期八年级4月期中数学评估试卷(含答案) | 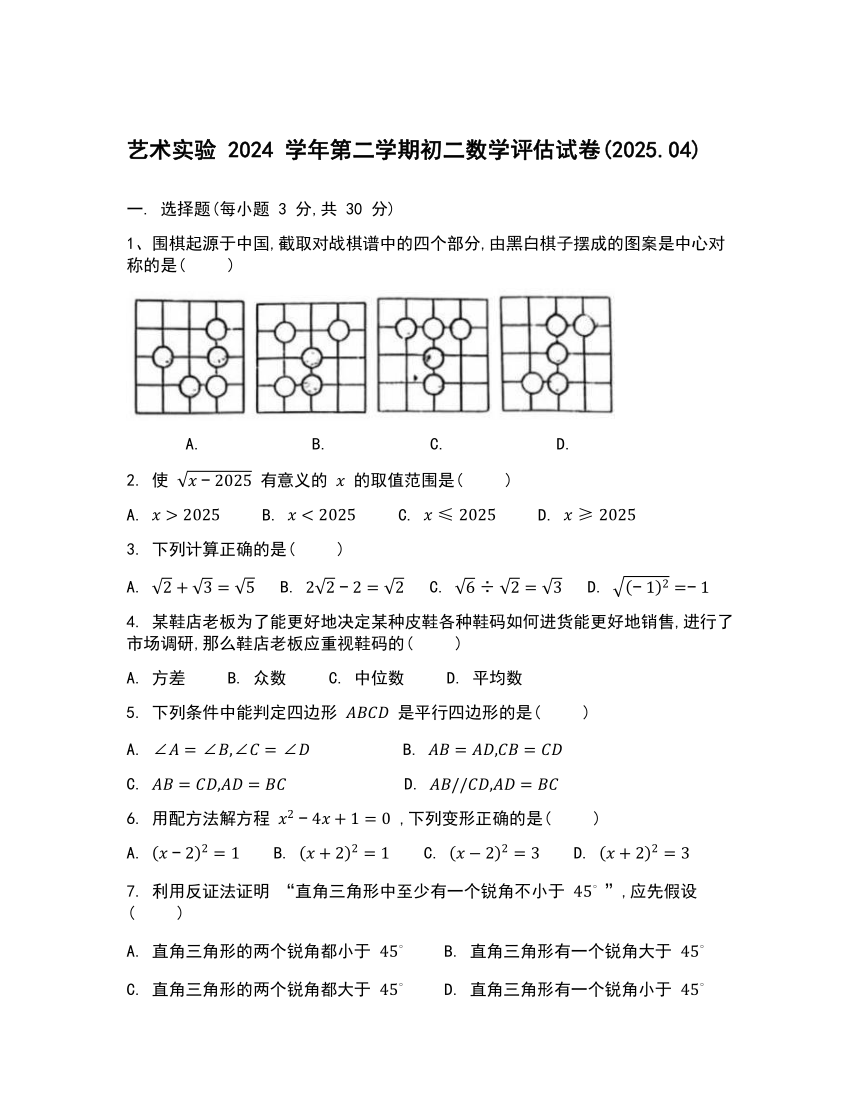 | |
| 格式 | docx | ||
| 文件大小 | 364.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 16:38:23 | ||
图片预览





文档简介
艺术实验 2024 学年第二学期初二数学评估试卷(2025.04)
一. 选择题(每小题 3 分,共 30 分)
1、围棋起源于中国,截取对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )
B. C. D.
2. 使 有意义的 的取值范围是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 某鞋店老板为了能更好地决定某种皮鞋各种鞋码如何进货能更好地销售,进行了市场调研,那么鞋店老板应重视鞋码的( )
A. 方差 B. 众数 C. 中位数 D. 平均数
5. 下列条件中能判定四边形 是平行四边形的是( )
A. B.
C. D.
6. 用配方法解方程 ,下列变形正确的是( )
A. B. C. D.
7. 利用反证法证明 “直角三角形中至少有一个锐角不小于 ”,应先假设( )
A. 直角三角形的两个锐角都小于 B. 直角三角形有一个锐角大于
C. 直角三角形的两个锐角都大于 D. 直角三角形有一个锐角小于
8. 在长为 ,宽为 的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为 , 求道路的宽度设道路的宽度为 ,则可列方程 ( ) .
A. B.
C. D.
9. 已知点 在双曲线 上,若 ,且 ,则 , 的大小关系是( )
A. B. C. D.
10. 如图,在 中,以 和 为斜边分别向内作等腰 和等腰 ,延长 和 分别交 和 于点 和 ,直线 分别交 和 于点 和 . 若四边形 是正方形, 的面积为 ,下列哪条线段的长度不能用 来表示 ( )
A. B. C. D.
二. 填空题(每小题 3 分,共 18 分)
11. 边形的内角和是 ,则 _____.
12. 若关于 的一元二次方程 有两个相等的实数根,则 的值为_____.
13. 观察下列算式:① ,② ,③ ...由此规律猜想第 7 个算式为:_____
14. 如图,在平面直角坐标系 中,函数 的图象经过 的斜边 的中点 , 交 于点 . 若点 在 轴上,点 的坐标为(12,8),则 的面积为_____.
(第 14 题图) (第 15 题图) (第 16 题图)
15. 如图,在 中, 是对角线, , 是 的中点, 平分 ,连结 , . 若 ,则 的长为_____
16. 如图,在等腰 △ABC中, , ,点 从点 出发沿 方向以 的速度向点 匀速运动,同时点 从点 出发沿 方向以 的速度向点 匀速运动,当其中一个点达到终点时,另一点也随之停止运动,设点 运动的时间为 秒. 过点 作 于点 ,若平面内存在一点 ,使得以 、 、 、 为顶点的四边形为菱形,则 的值为_____.
三. 解答题(第 17~19 题各 6 分,第 20~22 题各 8 分,第 23 题 10 分,共 52 分)
17.(6 分)计算:
(1) ; (2) .
18.(6 分)解方程:
(1) ; (2) .
19.(6 分)某学校从九年级同学中任意选取 40 人,随机分成甲、乙两个小组(每组 20 人)进行“引体向上” 体能测试, 根据测试成绩绘制出下面的统计表和统计图.
乙组成绩统计图甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
请根据上面的信息,解答下列问题:
(1)甲组成绩的中位数是_____ ,乙组成绩的众数是_____;
(2)请求出乙组成绩的平均数;
( 3 )已知甲组成绩的方差为 0.81 ,乙组成绩的方差为 0.75 ,请判断哪个小组的成绩更加稳定.
20. (8分)如图,在菱形 中, 是 的中点,连接 并延长,交 的延长线于点 .
(1)求证: ;
(2)若 ,求 的面积.
21. (8 分)如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时, 活塞受到托盘中重物的压力向下压缩装置内的空气. 某同学试着放上不同质量的物体, 并根据筒侧的刻度记录活塞到筒底的距离, 得到下面 5 组数据:
重物质量 2 3 4 6 8
活塞到桶底的距离 24 16 12 8 6
① ②
(1)以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连结.
(2)能否用学过的函数刻画变量 和 之间的关系?如果能,请求出 关于 的解析式;如果不能, 请说明理由.
(3)要使活塞到筒底的距离大于 5,请直接写出在托盘中放入重物的质量 的取值范围.
22. (8分)某超市于今年年初以每件 25 元的进价购进一批商品. 当商品售价为 40 元时,一月份销售 256 件. 二、三月该商品十分畅销. 销售量持续走高. 在售价不变的基础上, 三月底的销售量达到 400 件. 设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价 1 元,销售量增加 5 件,当商品降价多少元时,商场获利 4250 元
23. (10分) 如图 1 ,四边形 为正方形, 为对角线 上一点,连接 , .
(1)求证: ;
(2)如图 2 ,过点 作 ,交边 于点 ,以 , 为邻边作矩形 ,连接 . ①求证:矩形 是正方形;
②若正方形 的边长为 9, ,求正方形 的边长.
四. 附加题 (第 题各 3 分,第 3 题 4 分,共 10 分)
1. 实数 满足 ,且 ,则 _____.
2. 将四个全等的三角形按如图所示的方式围成一个正方形 ,记 的面积为 ,四边形 的面积为 . 若 ,则图中阴影部分的面积为_____.
3. 如果菱形有一条对角线等于它的边长, 那么称此菱形为 “完美菱形”. 如图,已知 “完美菱形” ABCD 的边长为 是它的较短对角线,点 分别是边 上的两个动点,且 ,点 为 的中点,点 为 边上的动点,则 的最小值为_____.
参考答案
1-8:DDCBCCAA
9: 解析: 反比例函数 的图象过第一、三象限,且在每个象限内, 随 的增大而减小. 又 ,且 . 又 . .
综上所述, .
故选: B .
10:解析设 ,
,
四边形 是平行四边形,
,
以 和 为斜边分别向内作等腰 和等腰 ,
,
,
四边形 是正方形,
,
,
,
,
即 ,
在 和 中,
,
,
, ,
,
,
是等腰直角三角形且 ,
由勾股定理得 ,
同理得 是等腰直角三角形,
由勾股定理得 ,
在等腰直角 中,由勾股定理得
,
,
的长度无法用 来表示,
故选: .
11:12
12:4
13:
14:12
15:解析如图,延长 、 交于点 ,
四边形 是平行四边形,
,
,
,
平分 ,
,
在 和 中,
,
,
,
点 是 的中点, ,
,
故答案为: .
16:解析过点 作 的垂线,垂足为 ,如图所示,
是等腰直角三角形, ,且
,
.
点 的运动速度为 ,点 的速度为 ,
,
是等腰直角三角形,
,
.
在 中,
(cm)
是等腰直角三角形,
,
,
是等腰直角三角形,
.
以 为顶点的四边形为菱形,
当 为等腰三角形时满足要求.
当 时,即 ,
,
解得 ,
又 ,
.
当 时,即 ,
,
解得 ,
当 时,点 , 与点 重合,故此情况不存在,
.
当 时,即 ,
,
解得 ,
当 时,点 , 与点 重合,故此情况不存在,
.
综上所述, 的值为 或 或5.
故答案为: 或 或5
17:解析(1)
;
(2)
.
18:解析(1) ,
或 ,
解得 ;
(2) ,
或
解得 .
19;解析(1)把甲组成绩从小到大排列,中位数是第 10、11 个数的平均数,
则中位教是 ,
乙组成绩(8分)出现的次数最多,出现了 9 次,
则乙组成绩的众数是 8 .
故答案为:8.5,8;
(2)乙组成绩的平均数为
(分);
(3)乙组的方差是:
,
乙组的成绩更加稳定.
20:解析(1)证明: 四边形 是菱形,
,
,
是 的中点,
,
,
,
.
(2)由(1)知 ,
,
,
,
,
,
的面积 .
21:解析(1)如图,
(2)猜想: 和 符合反比例函数关系,设 ,
将点(2,24)代入,得 ,
解得: ,
,
验证:当 时, ,符合题意,
关于 的解析式为 ;
(3) 由题意可得: ,即 ,
解得: ,
结合函数图象可得,重物的质量 的取值范围为
22:解析(1)设二、三这两个月的月平均增长率为 ,根据题意可得:
解得: , (不合题意舍去)。
答:二、三这两个月的月平均增长率为 ;
(2)设当商品降价 元时,商品获利4250元,根据题意可得:
,
解得: , (不合题意舍去)。
答: 当商品降价5元时,商场获利4250元.
23:解析(1)证明: 四边形 为正方形,
,
在 和 中,
,
;
(2)①证明:如图,作 于 , 于 , 得矩形 ,
图2
,
点 是正方形 对角线上的点,
,
,
,
,
在 和 中,
,
,
四边形 是矩形,
矩形 是正方形;
② 正方形 和正方形 ,
,
,
,
在 和 中,
,
,
,
,
,
.
,
,
连接 ,
图2
,
.
正方形 的边长为 .
附加题
1: ,且 ,
,
,
,
,
,
,
,
故答案为: .
2:连接 ,如图所示:
依题意得 , , ,
,
四边形 为正方形,
,
即 ,
在 和 中,
,
,
同理: ,
,
四边形 为菱形,
,
又 ,
, , 在同一条直线上,
,
,
菱形 为正方形,
,
同理: 在同一条直线上, 在同一条直线上, , , 在同一条直线上,
设 ,则 ,
,
,
,
整理得: ,
解得: , (不合题意,舍去),
,
.
3:设 与 的交点为 ,连接 , ,
四边形 是菱形,
,
,
,
的最小值为 ,
作点 关于 的对称点 ,延长 交 于点 ,连接 ,
,
的最小值为 ,
四边形 是菱形, ,
,
四边形 是“完美菱形” 的边长为8,
,
,
在 中, ,
,
由对称性和菱形的性质,知 ,
在 中,
,
的最小值为 ,
故答案为: .
一. 选择题(每小题 3 分,共 30 分)
1、围棋起源于中国,截取对战棋谱中的四个部分,由黑白棋子摆成的图案是中心对称的是( )
B. C. D.
2. 使 有意义的 的取值范围是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B. C. D.
4. 某鞋店老板为了能更好地决定某种皮鞋各种鞋码如何进货能更好地销售,进行了市场调研,那么鞋店老板应重视鞋码的( )
A. 方差 B. 众数 C. 中位数 D. 平均数
5. 下列条件中能判定四边形 是平行四边形的是( )
A. B.
C. D.
6. 用配方法解方程 ,下列变形正确的是( )
A. B. C. D.
7. 利用反证法证明 “直角三角形中至少有一个锐角不小于 ”,应先假设( )
A. 直角三角形的两个锐角都小于 B. 直角三角形有一个锐角大于
C. 直角三角形的两个锐角都大于 D. 直角三角形有一个锐角小于
8. 在长为 ,宽为 的长方形田地中开辟三条入口宽度相等的道路,已知剩余田地的面积为 , 求道路的宽度设道路的宽度为 ,则可列方程 ( ) .
A. B.
C. D.
9. 已知点 在双曲线 上,若 ,且 ,则 , 的大小关系是( )
A. B. C. D.
10. 如图,在 中,以 和 为斜边分别向内作等腰 和等腰 ,延长 和 分别交 和 于点 和 ,直线 分别交 和 于点 和 . 若四边形 是正方形, 的面积为 ,下列哪条线段的长度不能用 来表示 ( )
A. B. C. D.
二. 填空题(每小题 3 分,共 18 分)
11. 边形的内角和是 ,则 _____.
12. 若关于 的一元二次方程 有两个相等的实数根,则 的值为_____.
13. 观察下列算式:① ,② ,③ ...由此规律猜想第 7 个算式为:_____
14. 如图,在平面直角坐标系 中,函数 的图象经过 的斜边 的中点 , 交 于点 . 若点 在 轴上,点 的坐标为(12,8),则 的面积为_____.
(第 14 题图) (第 15 题图) (第 16 题图)
15. 如图,在 中, 是对角线, , 是 的中点, 平分 ,连结 , . 若 ,则 的长为_____
16. 如图,在等腰 △ABC中, , ,点 从点 出发沿 方向以 的速度向点 匀速运动,同时点 从点 出发沿 方向以 的速度向点 匀速运动,当其中一个点达到终点时,另一点也随之停止运动,设点 运动的时间为 秒. 过点 作 于点 ,若平面内存在一点 ,使得以 、 、 、 为顶点的四边形为菱形,则 的值为_____.
三. 解答题(第 17~19 题各 6 分,第 20~22 题各 8 分,第 23 题 10 分,共 52 分)
17.(6 分)计算:
(1) ; (2) .
18.(6 分)解方程:
(1) ; (2) .
19.(6 分)某学校从九年级同学中任意选取 40 人,随机分成甲、乙两个小组(每组 20 人)进行“引体向上” 体能测试, 根据测试成绩绘制出下面的统计表和统计图.
乙组成绩统计图甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
请根据上面的信息,解答下列问题:
(1)甲组成绩的中位数是_____ ,乙组成绩的众数是_____;
(2)请求出乙组成绩的平均数;
( 3 )已知甲组成绩的方差为 0.81 ,乙组成绩的方差为 0.75 ,请判断哪个小组的成绩更加稳定.
20. (8分)如图,在菱形 中, 是 的中点,连接 并延长,交 的延长线于点 .
(1)求证: ;
(2)若 ,求 的面积.
21. (8 分)如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时, 活塞受到托盘中重物的压力向下压缩装置内的空气. 某同学试着放上不同质量的物体, 并根据筒侧的刻度记录活塞到筒底的距离, 得到下面 5 组数据:
重物质量 2 3 4 6 8
活塞到桶底的距离 24 16 12 8 6
① ②
(1)以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连结.
(2)能否用学过的函数刻画变量 和 之间的关系?如果能,请求出 关于 的解析式;如果不能, 请说明理由.
(3)要使活塞到筒底的距离大于 5,请直接写出在托盘中放入重物的质量 的取值范围.
22. (8分)某超市于今年年初以每件 25 元的进价购进一批商品. 当商品售价为 40 元时,一月份销售 256 件. 二、三月该商品十分畅销. 销售量持续走高. 在售价不变的基础上, 三月底的销售量达到 400 件. 设二、三这两个月的月平均增长率不变.
(1)求二、三这两个月的月平均增长率;
(2)从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价 1 元,销售量增加 5 件,当商品降价多少元时,商场获利 4250 元
23. (10分) 如图 1 ,四边形 为正方形, 为对角线 上一点,连接 , .
(1)求证: ;
(2)如图 2 ,过点 作 ,交边 于点 ,以 , 为邻边作矩形 ,连接 . ①求证:矩形 是正方形;
②若正方形 的边长为 9, ,求正方形 的边长.
四. 附加题 (第 题各 3 分,第 3 题 4 分,共 10 分)
1. 实数 满足 ,且 ,则 _____.
2. 将四个全等的三角形按如图所示的方式围成一个正方形 ,记 的面积为 ,四边形 的面积为 . 若 ,则图中阴影部分的面积为_____.
3. 如果菱形有一条对角线等于它的边长, 那么称此菱形为 “完美菱形”. 如图,已知 “完美菱形” ABCD 的边长为 是它的较短对角线,点 分别是边 上的两个动点,且 ,点 为 的中点,点 为 边上的动点,则 的最小值为_____.
参考答案
1-8:DDCBCCAA
9: 解析: 反比例函数 的图象过第一、三象限,且在每个象限内, 随 的增大而减小. 又 ,且 . 又 . .
综上所述, .
故选: B .
10:解析设 ,
,
四边形 是平行四边形,
,
以 和 为斜边分别向内作等腰 和等腰 ,
,
,
四边形 是正方形,
,
,
,
,
即 ,
在 和 中,
,
,
, ,
,
,
是等腰直角三角形且 ,
由勾股定理得 ,
同理得 是等腰直角三角形,
由勾股定理得 ,
在等腰直角 中,由勾股定理得
,
,
的长度无法用 来表示,
故选: .
11:12
12:4
13:
14:12
15:解析如图,延长 、 交于点 ,
四边形 是平行四边形,
,
,
,
平分 ,
,
在 和 中,
,
,
,
点 是 的中点, ,
,
故答案为: .
16:解析过点 作 的垂线,垂足为 ,如图所示,
是等腰直角三角形, ,且
,
.
点 的运动速度为 ,点 的速度为 ,
,
是等腰直角三角形,
,
.
在 中,
(cm)
是等腰直角三角形,
,
,
是等腰直角三角形,
.
以 为顶点的四边形为菱形,
当 为等腰三角形时满足要求.
当 时,即 ,
,
解得 ,
又 ,
.
当 时,即 ,
,
解得 ,
当 时,点 , 与点 重合,故此情况不存在,
.
当 时,即 ,
,
解得 ,
当 时,点 , 与点 重合,故此情况不存在,
.
综上所述, 的值为 或 或5.
故答案为: 或 或5
17:解析(1)
;
(2)
.
18:解析(1) ,
或 ,
解得 ;
(2) ,
或
解得 .
19;解析(1)把甲组成绩从小到大排列,中位数是第 10、11 个数的平均数,
则中位教是 ,
乙组成绩(8分)出现的次数最多,出现了 9 次,
则乙组成绩的众数是 8 .
故答案为:8.5,8;
(2)乙组成绩的平均数为
(分);
(3)乙组的方差是:
,
乙组的成绩更加稳定.
20:解析(1)证明: 四边形 是菱形,
,
,
是 的中点,
,
,
,
.
(2)由(1)知 ,
,
,
,
,
,
的面积 .
21:解析(1)如图,
(2)猜想: 和 符合反比例函数关系,设 ,
将点(2,24)代入,得 ,
解得: ,
,
验证:当 时, ,符合题意,
关于 的解析式为 ;
(3) 由题意可得: ,即 ,
解得: ,
结合函数图象可得,重物的质量 的取值范围为
22:解析(1)设二、三这两个月的月平均增长率为 ,根据题意可得:
解得: , (不合题意舍去)。
答:二、三这两个月的月平均增长率为 ;
(2)设当商品降价 元时,商品获利4250元,根据题意可得:
,
解得: , (不合题意舍去)。
答: 当商品降价5元时,商场获利4250元.
23:解析(1)证明: 四边形 为正方形,
,
在 和 中,
,
;
(2)①证明:如图,作 于 , 于 , 得矩形 ,
图2
,
点 是正方形 对角线上的点,
,
,
,
,
在 和 中,
,
,
四边形 是矩形,
矩形 是正方形;
② 正方形 和正方形 ,
,
,
,
在 和 中,
,
,
,
,
,
.
,
,
连接 ,
图2
,
.
正方形 的边长为 .
附加题
1: ,且 ,
,
,
,
,
,
,
,
故答案为: .
2:连接 ,如图所示:
依题意得 , , ,
,
四边形 为正方形,
,
即 ,
在 和 中,
,
,
同理: ,
,
四边形 为菱形,
,
又 ,
, , 在同一条直线上,
,
,
菱形 为正方形,
,
同理: 在同一条直线上, 在同一条直线上, , , 在同一条直线上,
设 ,则 ,
,
,
,
整理得: ,
解得: , (不合题意,舍去),
,
.
3:设 与 的交点为 ,连接 , ,
四边形 是菱形,
,
,
,
的最小值为 ,
作点 关于 的对称点 ,延长 交 于点 ,连接 ,
,
的最小值为 ,
四边形 是菱形, ,
,
四边形 是“完美菱形” 的边长为8,
,
,
在 中, ,
,
由对称性和菱形的性质,知 ,
在 中,
,
的最小值为 ,
故答案为: .
同课章节目录
