第十九章一次函数单元测试(含答案)
图片预览
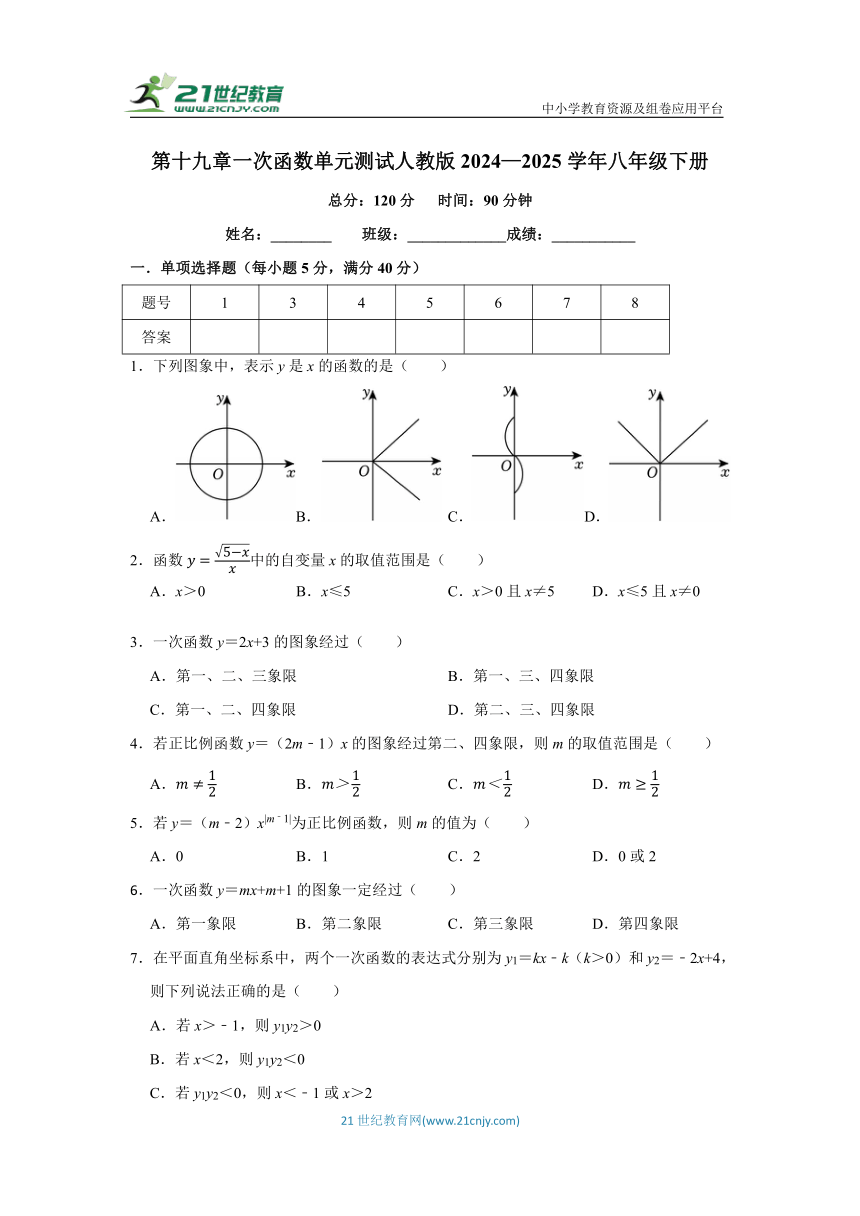


文档简介
中小学教育资源及组卷应用平台
第十九章一次函数单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列图象中,表示y是x的函数的是( )
A.B. C.D.
2.函数中的自变量x的取值范围是( )
A.x>0 B.x≤5 C.x>0且x≠5 D.x≤5且x≠0
3.一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
4.若正比例函数y=(2m﹣1)x的图象经过第二、四象限,则m的取值范围是( )
A. B. C. D.
5.若y=(m﹣2)x|m﹣1|为正比例函数,则m的值为( )
A.0 B.1 C.2 D.0或2
6.一次函数y=mx+m+1的图象一定经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在平面直角坐标系中,两个一次函数的表达式分别为y1=kx﹣k(k>0)和y2=﹣2x+4,则下列说法正确的是( )
A.若x>﹣1,则y1y2>0
B.若x<2,则y1y2<0
C.若y1y2<0,则x<﹣1或x>2
D.若y1y2>0,则1<x<2
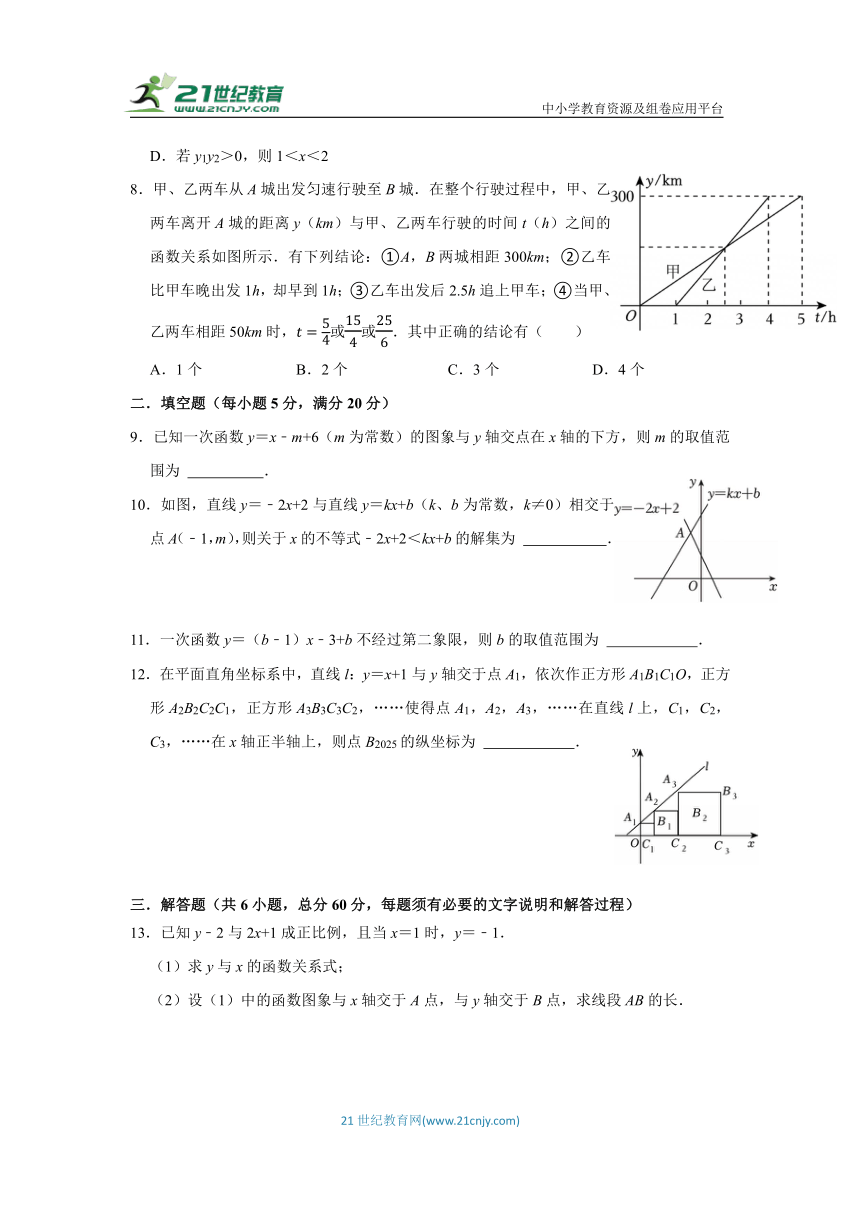
8.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲、乙两车行驶的时间t(h)之间的函数关系如图所示.有下列结论:①A,B两城相距300km;②乙车比甲车晚出发1h,却早到1h;③乙车出发后2.5h追上甲车;④当甲、乙两车相距50km时,或或.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题5分,满分20分)
9.已知一次函数y=x﹣m+6(m为常数)的图象与y轴交点在x轴的下方,则m的取值范围为 .
10.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),则关于x的不等式﹣2x+2<kx+b的解集为 .
11.一次函数y=(b﹣1)x﹣3+b不经过第二象限,则b的取值范围为 .
12.在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,依次作正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,……使得点A1,A2,A3,……在直线l上,C1,C2,C3,……在x轴正半轴上,则点B2025的纵坐标为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知y﹣2与2x+1成正比例,且当x=1时,y=﹣1.
(1)求y与x的函数关系式;
(2)设(1)中的函数图象与x轴交于A点,与y轴交于B点,求线段AB的长.
14.一次函数y=kx﹣k+2(k为常数,且k≠0).
(1)若点(﹣1,3)在一次函数y=kx﹣k+2的图象上,
①求k的值;
②设P=y+x,则当﹣2≤x≤5时,求P的最大值.
(2)若当m﹣3≤x≤m时,函数有最大值M,最小值N,且M﹣N=6,求此时一次函数y的表达式.
15.某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
16.已知一次函数y1=kx+b,y2=bx﹣2k+3(其中k、b为常数且k≠0,b≠0)
(1)若y1与y2的图象交于点(2,3),求k,b的值;
(2)若b=k﹣1,当﹣2≤x≤2时,函数y1有最大值3,求此时一次函数y1的表达式.
(3)若对任意实数x,y1>y2都成立,求k的取值范围.
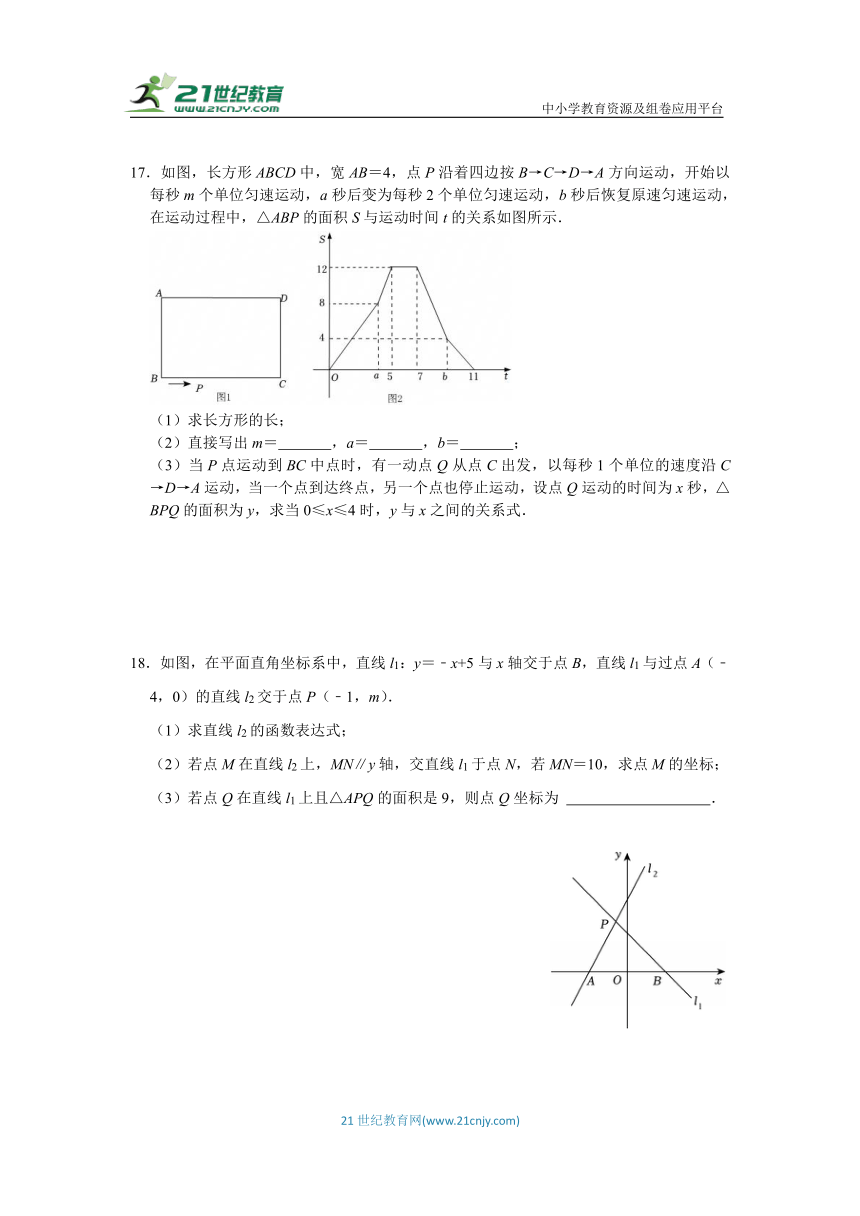
17.如图,长方形ABCD中,宽AB=4,点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,△ABP的面积S与运动时间t的关系如图所示.
(1)求长方形的长;
(2)直接写出m= ,a= ,b= ;
(3)当P点运动到BC中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,△BPQ的面积为y,求当0≤x≤4时,y与x之间的关系式.
18.如图,在平面直角坐标系中,直线l1:y=﹣x+5与x轴交于点B,直线l1与过点A(﹣4,0)的直线l2交于点P(﹣1,m).
(1)求直线l2的函数表达式;
(2)若点M在直线l2上,MN∥y轴,交直线l1于点N,若MN=10,求点M的坐标;
(3)若点Q在直线l1上且△APQ的面积是9,则点Q坐标为 .
参考答案
一、选择题
1—8:DDACABDC
二、填空题
9.【解答】解:∵函数图象与y轴的交点在x轴下方,
∴﹣m+6<0,
∴解得m>6,
∴m的取值范围为m>6.
故答案为:为m>6.
10.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),
∴x>﹣1时,﹣2x+2<kx+b.
∴关于x的不等式﹣2x+2<kx+b的解集为x>﹣1.
故答案为:x>﹣1.
11.【解答】解:∵一次函数y=(b﹣1)x﹣3+b不经过第二象限,
∴函数图象经过第一、三象限或函数图象经过第一、三、四象限,
∴b﹣1>0且﹣3+b≤0,
解得1<b≤3.
故答案为:1<b≤3.
12.【解答】解:对于y=x+1,当x=0时,y=1,当y=0时,x=﹣1,
∴点A1(0,1),点C(﹣1,0),如图所示:
∴OA1=OC=1,
∴△OA1C是等腰直角三角形,
∴∠A1CO=45°,
∵OA1B1C1是正方形,
∴A1B1∥x轴,A1B1=OA1=B1C1=1,
∴∠A2A1B1=∠A1CO=45°,点B1的纵坐标为1,即20=1,
∴△A2A1B1是等腰直角三角形,
∴A2B1=A1B1=1,
∴A2C2=2,
∵四边形A2B2C2C1是正方形,
∴B2C2=A2C1=2,
∴点B2的纵坐标为2,即21=2,
同理得:B3C3=A3C2=4,
∴点B3的纵坐标为4,即22=4,
…,以此类推,点Bn的纵坐标为:2n﹣1,
∴点B2025的纵坐标为:22024.
故答案为:22024.
三、解答题
13.【解答】解:(1)∵y﹣2与2x+1成正比例,
∴可以设y﹣2=k(2x+1),
∵当x=1时,y=﹣1,
∴﹣1﹣2=k(2×1+1),
解得k=﹣1,
∴y﹣2=﹣(2x+1),
∴y=﹣2x+1,
即y与x的函数关系式是y=﹣2x+1;
(2)由(1)知,y=﹣2x+1,
∴当x=0时,y=1;当y=0时,x=0.5;
∵(1)中的函数图象与x轴交于A点,与y轴交于B点,
∴点A的坐标为(0.5,0),点B的坐标为(0,1),
∴OA=0.5,OB=1,
∴AB,
即线段AB的长为.
14.【解答】解:(1)①把(﹣1,3)代入y=kx﹣k+2得﹣k﹣k+2=3,
解得k;
②当k时,yx,
∴P=x+y=xxx,
∵y随x的增大而增大,
∴当﹣2≤x≤5时,x=5时,P的值最大,
当x=5时,P54,
即P的最大值为4;
(2)当k>0时,M=km﹣k+2,N=k(m﹣3)﹣k+2,
∵M﹣N=6,
∴km﹣k+2﹣[k(m﹣3)﹣k+2]=6,
解得k=2,
此时一次函数解析式为y=2x;
当k<0时,N=km﹣k+2,M=k(m﹣3)﹣k+2,
∵M﹣N=6,
∴k(m﹣3)﹣k+2﹣(km﹣k+2)=6,
解得k=﹣2,
此时一次函数解析式为y=﹣2x+4;
综上所述,一次函数解析式为y=2x或y=﹣2x+4.
15.【解答】解:(1)根据题意,y=400x+500(100﹣x)=﹣100x+50000;
(2)∵100﹣x≤2x,
∴x,
∵y=﹣100x+50000中k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为46600,
答:该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;
(3)据题意得,y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,
当a=100时,无论该公司如何进货这100台电脑的销售利润不变.
16.【解答】解:(1)把(2,3)代入y1,y2,得:
,解得:;
(2)若b=k﹣1,则:y1=kx+k﹣1,
①当k>0时,y随x的增大而增大,
∵﹣2≤x≤2,
∴当x=2时,y有最大值为2k+k﹣1=3,解得:;
∴;
①当k<0时,y随x的增大而减小,
∵﹣2≤x≤2,
∴当x=﹣2时,y有最大值为﹣2k+k﹣1=3,解得:k=﹣4;
∴y1=﹣4x﹣5
综上:或y1=﹣4x﹣5.
(3)由题意:两条直线平行且直线y1在直线y2的上方,
∴k=b,b>﹣2k+3,
∴k>﹣2k+3,
∴k>1.
17.【解答】解:(1)在5≤x≤7时,△ABP的面积不变,
此时:点P在CD上运动,速度为每秒2个单位,
∴AB=CD=2×2=4,
在5≤x≤7时,△ABP的面积为12,
∴4×BC=12,
∴BC=6,
∴长方形的长为6.
(2)当x=a时,S△ABP4×BP=8,
∴BP=4,
∴CP=2,
∴a=5﹣(2÷2)=4,
∴m1,
当x=b时,S△ABP4×AP=4,
∴AP=2,
∴DP=4,
∴b=7+(4÷2)=9;
故答案为:1;4;9;
(3)根据题意可知,BC=4×1+1×2=6,CD=2×2=4;
当0≤x≤1时,如图,BP=3+x,CQ=x,
∴yBP CQ(3+x) xx2x;
当1<x≤2时,如图,BP=4+2(x﹣1)=2x+2,CQ=x,
yBP CQ(2x+2) x=x2+x;
当2<x≤4时,如图,CP=2(x﹣2),CQ=x,
∴PQ=x﹣(2x﹣4)=4﹣x,
∴yPQ BC(4﹣x) 6=12﹣3x;
∴y.
18.【解答】解:(1)将点P(﹣1,m)代入y=﹣x+5得:m=﹣(﹣1)+5=6,
∴点P(﹣1,6),
设直线l2的函数表达式为:y=kx+b(k≠0),
将P(﹣1,6)和A(﹣4,0)代入y=kx+b得:
,
解得:,
∴直线l2的函数表达式为:y=2x+8;
(2)设点M的横坐标为n,
∴点M的坐标为(n,2n+8),
∵MN∥y轴,∴N(n,﹣n+5),
由题意得MN=|2n+8﹣(﹣n+5)|=10,
整理得,3n+3=±10,
解得:或,
故点M的坐标为或;
(3)在直线l1中,当y=0时,则﹣x+5=0,
解得:x=5,
∴点B(5,0),
∴AB=5+4=9,
设点Q的坐标为(a,﹣a+5),
根据题意得S9,
即|1+a|=2,
解得a=﹣3或a=1,
∴点Q的坐标为(﹣3,8)或(1,4),
故答案为:(﹣3,8)或(1,4).
21世纪教育网(www.21cnjy.com)
第十九章一次函数单元测试人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列图象中,表示y是x的函数的是( )
A.B. C.D.
2.函数中的自变量x的取值范围是( )
A.x>0 B.x≤5 C.x>0且x≠5 D.x≤5且x≠0
3.一次函数y=2x+3的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
4.若正比例函数y=(2m﹣1)x的图象经过第二、四象限,则m的取值范围是( )
A. B. C. D.
5.若y=(m﹣2)x|m﹣1|为正比例函数,则m的值为( )
A.0 B.1 C.2 D.0或2
6.一次函数y=mx+m+1的图象一定经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.在平面直角坐标系中,两个一次函数的表达式分别为y1=kx﹣k(k>0)和y2=﹣2x+4,则下列说法正确的是( )
A.若x>﹣1,则y1y2>0
B.若x<2,则y1y2<0
C.若y1y2<0,则x<﹣1或x>2
D.若y1y2>0,则1<x<2
8.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲、乙两车行驶的时间t(h)之间的函数关系如图所示.有下列结论:①A,B两城相距300km;②乙车比甲车晚出发1h,却早到1h;③乙车出发后2.5h追上甲车;④当甲、乙两车相距50km时,或或.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(每小题5分,满分20分)
9.已知一次函数y=x﹣m+6(m为常数)的图象与y轴交点在x轴的下方,则m的取值范围为 .
10.如图,直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),则关于x的不等式﹣2x+2<kx+b的解集为 .
11.一次函数y=(b﹣1)x﹣3+b不经过第二象限,则b的取值范围为 .
12.在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,依次作正方形A1B1C1O,正方形A2B2C2C1,正方形A3B3C3C2,……使得点A1,A2,A3,……在直线l上,C1,C2,C3,……在x轴正半轴上,则点B2025的纵坐标为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知y﹣2与2x+1成正比例,且当x=1时,y=﹣1.
(1)求y与x的函数关系式;
(2)设(1)中的函数图象与x轴交于A点,与y轴交于B点,求线段AB的长.
14.一次函数y=kx﹣k+2(k为常数,且k≠0).
(1)若点(﹣1,3)在一次函数y=kx﹣k+2的图象上,
①求k的值;
②设P=y+x,则当﹣2≤x≤5时,求P的最大值.
(2)若当m﹣3≤x≤m时,函数有最大值M,最小值N,且M﹣N=6,求此时一次函数y的表达式.
15.某公司销售A型和B型两种电脑,其中A型电脑每台利润为400元,B型电脑每台利润为500元.该公司计划一次性购进这两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,若该公司保持这两种型号电脑的售价不变,并且无论该公司如何进货这100台电脑的销售利润不变,求a的值.
16.已知一次函数y1=kx+b,y2=bx﹣2k+3(其中k、b为常数且k≠0,b≠0)
(1)若y1与y2的图象交于点(2,3),求k,b的值;
(2)若b=k﹣1,当﹣2≤x≤2时,函数y1有最大值3,求此时一次函数y1的表达式.
(3)若对任意实数x,y1>y2都成立,求k的取值范围.
17.如图,长方形ABCD中,宽AB=4,点P沿着四边按B→C→D→A方向运动,开始以每秒m个单位匀速运动,a秒后变为每秒2个单位匀速运动,b秒后恢复原速匀速运动,在运动过程中,△ABP的面积S与运动时间t的关系如图所示.
(1)求长方形的长;
(2)直接写出m= ,a= ,b= ;
(3)当P点运动到BC中点时,有一动点Q从点C出发,以每秒1个单位的速度沿C→D→A运动,当一个点到达终点,另一个点也停止运动,设点Q运动的时间为x秒,△BPQ的面积为y,求当0≤x≤4时,y与x之间的关系式.
18.如图,在平面直角坐标系中,直线l1:y=﹣x+5与x轴交于点B,直线l1与过点A(﹣4,0)的直线l2交于点P(﹣1,m).
(1)求直线l2的函数表达式;
(2)若点M在直线l2上,MN∥y轴,交直线l1于点N,若MN=10,求点M的坐标;
(3)若点Q在直线l1上且△APQ的面积是9,则点Q坐标为 .
参考答案
一、选择题
1—8:DDACABDC
二、填空题
9.【解答】解:∵函数图象与y轴的交点在x轴下方,
∴﹣m+6<0,
∴解得m>6,
∴m的取值范围为m>6.
故答案为:为m>6.
10.【解答】解:∵直线y=﹣2x+2与直线y=kx+b(k、b为常数,k≠0)相交于点A(﹣1,m),
∴x>﹣1时,﹣2x+2<kx+b.
∴关于x的不等式﹣2x+2<kx+b的解集为x>﹣1.
故答案为:x>﹣1.
11.【解答】解:∵一次函数y=(b﹣1)x﹣3+b不经过第二象限,
∴函数图象经过第一、三象限或函数图象经过第一、三、四象限,
∴b﹣1>0且﹣3+b≤0,
解得1<b≤3.
故答案为:1<b≤3.
12.【解答】解:对于y=x+1,当x=0时,y=1,当y=0时,x=﹣1,
∴点A1(0,1),点C(﹣1,0),如图所示:
∴OA1=OC=1,
∴△OA1C是等腰直角三角形,
∴∠A1CO=45°,
∵OA1B1C1是正方形,
∴A1B1∥x轴,A1B1=OA1=B1C1=1,
∴∠A2A1B1=∠A1CO=45°,点B1的纵坐标为1,即20=1,
∴△A2A1B1是等腰直角三角形,
∴A2B1=A1B1=1,
∴A2C2=2,
∵四边形A2B2C2C1是正方形,
∴B2C2=A2C1=2,
∴点B2的纵坐标为2,即21=2,
同理得:B3C3=A3C2=4,
∴点B3的纵坐标为4,即22=4,
…,以此类推,点Bn的纵坐标为:2n﹣1,
∴点B2025的纵坐标为:22024.
故答案为:22024.
三、解答题
13.【解答】解:(1)∵y﹣2与2x+1成正比例,
∴可以设y﹣2=k(2x+1),
∵当x=1时,y=﹣1,
∴﹣1﹣2=k(2×1+1),
解得k=﹣1,
∴y﹣2=﹣(2x+1),
∴y=﹣2x+1,
即y与x的函数关系式是y=﹣2x+1;
(2)由(1)知,y=﹣2x+1,
∴当x=0时,y=1;当y=0时,x=0.5;
∵(1)中的函数图象与x轴交于A点,与y轴交于B点,
∴点A的坐标为(0.5,0),点B的坐标为(0,1),
∴OA=0.5,OB=1,
∴AB,
即线段AB的长为.
14.【解答】解:(1)①把(﹣1,3)代入y=kx﹣k+2得﹣k﹣k+2=3,
解得k;
②当k时,yx,
∴P=x+y=xxx,
∵y随x的增大而增大,
∴当﹣2≤x≤5时,x=5时,P的值最大,
当x=5时,P54,
即P的最大值为4;
(2)当k>0时,M=km﹣k+2,N=k(m﹣3)﹣k+2,
∵M﹣N=6,
∴km﹣k+2﹣[k(m﹣3)﹣k+2]=6,
解得k=2,
此时一次函数解析式为y=2x;
当k<0时,N=km﹣k+2,M=k(m﹣3)﹣k+2,
∵M﹣N=6,
∴k(m﹣3)﹣k+2﹣(km﹣k+2)=6,
解得k=﹣2,
此时一次函数解析式为y=﹣2x+4;
综上所述,一次函数解析式为y=2x或y=﹣2x+4.
15.【解答】解:(1)根据题意,y=400x+500(100﹣x)=﹣100x+50000;
(2)∵100﹣x≤2x,
∴x,
∵y=﹣100x+50000中k=﹣100<0,
∴y随x的增大而减小,
∵x为整数,
∴x=34时,y取得最大值,最大值为46600,
答:该商店购进A型34台、B型电脑66台,才能使销售总利润最大,最大利润是46600元;
(3)据题意得,y=(400+a)x+500(100﹣x),即y=(a﹣100)x+50000,
当a=100时,无论该公司如何进货这100台电脑的销售利润不变.
16.【解答】解:(1)把(2,3)代入y1,y2,得:
,解得:;
(2)若b=k﹣1,则:y1=kx+k﹣1,
①当k>0时,y随x的增大而增大,
∵﹣2≤x≤2,
∴当x=2时,y有最大值为2k+k﹣1=3,解得:;
∴;
①当k<0时,y随x的增大而减小,
∵﹣2≤x≤2,
∴当x=﹣2时,y有最大值为﹣2k+k﹣1=3,解得:k=﹣4;
∴y1=﹣4x﹣5
综上:或y1=﹣4x﹣5.
(3)由题意:两条直线平行且直线y1在直线y2的上方,
∴k=b,b>﹣2k+3,
∴k>﹣2k+3,
∴k>1.
17.【解答】解:(1)在5≤x≤7时,△ABP的面积不变,
此时:点P在CD上运动,速度为每秒2个单位,
∴AB=CD=2×2=4,
在5≤x≤7时,△ABP的面积为12,
∴4×BC=12,
∴BC=6,
∴长方形的长为6.
(2)当x=a时,S△ABP4×BP=8,
∴BP=4,
∴CP=2,
∴a=5﹣(2÷2)=4,
∴m1,
当x=b时,S△ABP4×AP=4,
∴AP=2,
∴DP=4,
∴b=7+(4÷2)=9;
故答案为:1;4;9;
(3)根据题意可知,BC=4×1+1×2=6,CD=2×2=4;
当0≤x≤1时,如图,BP=3+x,CQ=x,
∴yBP CQ(3+x) xx2x;
当1<x≤2时,如图,BP=4+2(x﹣1)=2x+2,CQ=x,
yBP CQ(2x+2) x=x2+x;
当2<x≤4时,如图,CP=2(x﹣2),CQ=x,
∴PQ=x﹣(2x﹣4)=4﹣x,
∴yPQ BC(4﹣x) 6=12﹣3x;
∴y.
18.【解答】解:(1)将点P(﹣1,m)代入y=﹣x+5得:m=﹣(﹣1)+5=6,
∴点P(﹣1,6),
设直线l2的函数表达式为:y=kx+b(k≠0),
将P(﹣1,6)和A(﹣4,0)代入y=kx+b得:
,
解得:,
∴直线l2的函数表达式为:y=2x+8;
(2)设点M的横坐标为n,
∴点M的坐标为(n,2n+8),
∵MN∥y轴,∴N(n,﹣n+5),
由题意得MN=|2n+8﹣(﹣n+5)|=10,
整理得,3n+3=±10,
解得:或,
故点M的坐标为或;
(3)在直线l1中,当y=0时,则﹣x+5=0,
解得:x=5,
∴点B(5,0),
∴AB=5+4=9,
设点Q的坐标为(a,﹣a+5),
根据题意得S9,
即|1+a|=2,
解得a=﹣3或a=1,
∴点Q的坐标为(﹣3,8)或(1,4),
故答案为:(﹣3,8)或(1,4).
21世纪教育网(www.21cnjy.com)
