2025年九年级数学中考三轮冲刺训练一次函数与几何综合压轴题练习(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练一次函数与几何综合压轴题练习(含解析) | 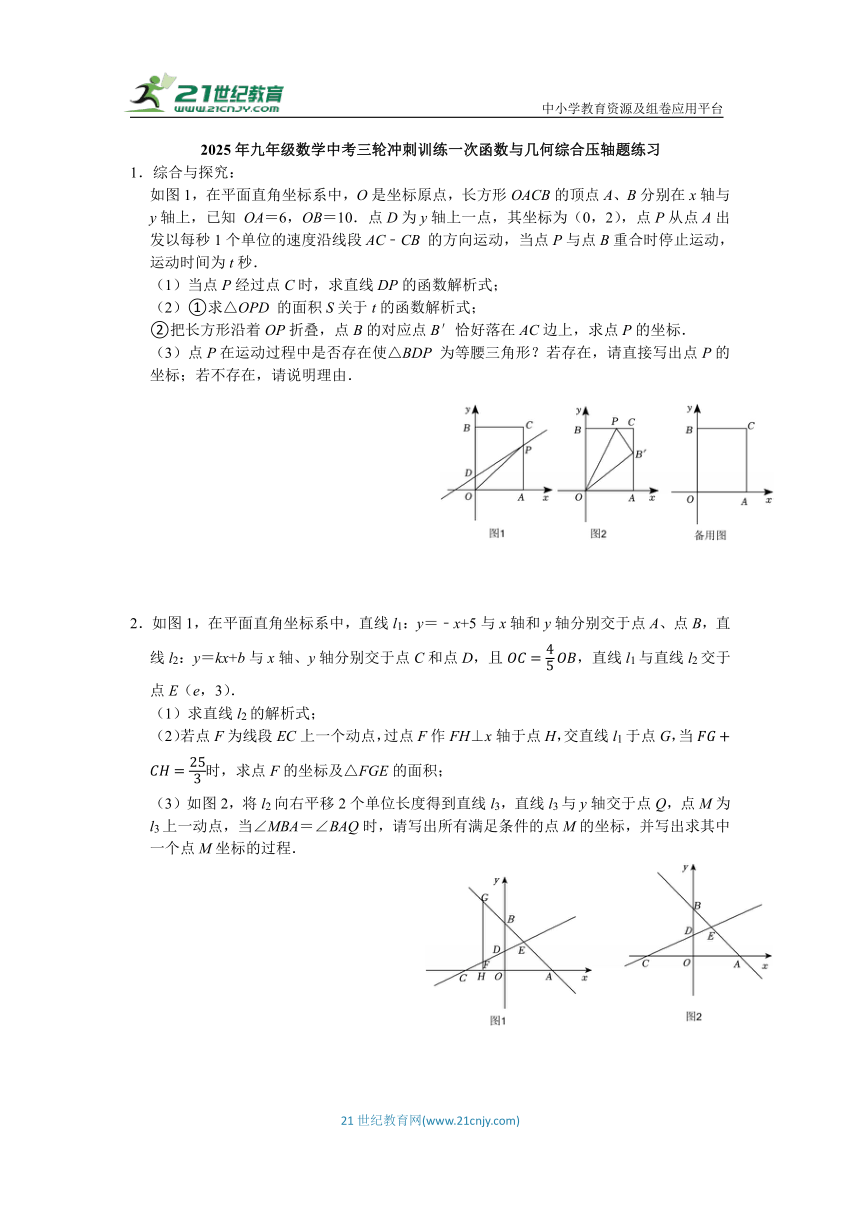 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 16:32:07 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练一次函数与几何综合压轴题练习
1.综合与探究:
如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知 OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB 的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD 的面积S关于t的函数解析式;
②把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP 为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2.如图1,在平面直角坐标系中,直线l1:y=﹣x+5与x轴和y轴分别交于点A、点B,直线l2:y=kx+b与x轴、y轴分别交于点C和点D,且,直线l1与直线l2交于点E(e,3).
(1)求直线l2的解析式;
(2)若点F为线段EC上一个动点,过点F作FH⊥x轴于点H,交直线l1于点G,当时,求点F的坐标及△FGE的面积;
(3)如图2,将l2向右平移2个单位长度得到直线l3,直线l3与y轴交于点Q,点M为l3上一动点,当∠MBA=∠BAQ时,请写出所有满足条件的点M的坐标,并写出求其中一个点M坐标的过程.
3.如图,在平面直角坐标系xOy中,直线y1=mx+n(m≠0)与x轴交于点A,与y轴交于点B(0,6),直线y2=x+2与y轴交于点P,与y1交于点C(3,a).点D为x轴上正半轴一动点,过点D作x轴的垂线与直线y1,y2分别相交于E,F两点,过点E作EH∥x轴的直线交y2于点H.
(1)求a的值及y1的函数表达式;
(2)当EF=4,求D点的坐标;
(3)以EF,EH为边作长方形EFMH,当点D在运动过程中,试探究M的运动轨迹是否为一条直线中的一部分?若是,直接写出该直线解析式;若不是,请说明理由.
4.如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,直线y=kx+5分别交x轴、y轴的正半轴于D,C两点,OC=OD,两直线相交于点E.
(1)求k的值与线段AB的长;
(2)若F为线段AE上的动点,
①连接FC,FD,S△CDF=10时,求点F的坐标;
②G为线段DE上的动点,当△ODG≌△GFO时,求点F的坐标.
5.如图,在平面直角坐标系xOy中,直线AB:y=ax+b(a<0)与y轴、x轴分别交于点A(0,8),B,AB的长为10,点C在y轴的负半轴上,以BC为对称轴作△ABC的轴对称图形,点A的对称点为点D.
(1)求直线AB的解析式;
(2)若点D恰好落在x轴正半轴上,求点D的坐标以及直线CD的解析式;
(3)当AB⊥BD时,直接写出点C的坐标.
6.平面直角坐标系xOy中有点A和点P,若将点P绕点A顺时针旋转90°后得到点Q,则称点Q为点P关于点A的“链垂点”,图1为点P关于点A的“链垂点”Q的示意图.
(1)如图2,已知点A的坐标为(0,0),点P关于点A的“链垂点”为点Q.
①若点P的坐标为(0,3),则点Q的坐标为 ;
②若点Q的坐标为(2,﹣1),则点P的坐标为 ;
(2)已知点C的坐标为(﹣2,0),点D在直线y=﹣2x+4上,若点D关于点C的“链垂点”E在坐标轴上,试求出点D的坐标;
(3)在平面直角坐标系xOy中,已知点A(﹣1,2),点C是x轴上的动点,点A关于点C的“链垂点”是点B,连接BO、BA.
①直接写出BO+BA的最小值;
②直接写出当BO+BA最小时点C的坐标.
7.如图,在平面直角坐标系xOy中,直线分别与x轴、y轴相交于点A、B,且与经过点C(0.﹣6)直线y=kx+b(k≠0)相交于点D.点D的横坐标为4,直线CD与x轴相交于点E.点P(m,n)是线段CD上一点(不含端点),连接BP.
(1)求直线CD的函数表达式;
(2)①若△BDP面积等于△BCP面积的一半,求m的值;
②点D′是点D关于直线BP对称点,连接D′E.当点P在线段CD上运动时,D′E是否存在最大值或最小值?若存在,请直接写出D′E的最值;若不存在,请说明理由;
(3)延长BP至Q,使PQ=BP,连接DQ.若直线y=mx+2n﹣21与△BDQ的边有两个交点,求m的取值范围.
8.如图,在平面直角坐标系中,直线AB:yx+12与x轴、y轴分别交于点A、B,点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处.
(1)求C点的坐标以及直线CD的解析式;
(2)点M是y轴上一动点,若S△MAB,求出点M的坐标;
(3)在第一象限内是否存在点P,使△PAB为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
9.如图,直线y=x+3与坐标轴分别交于点A,C,直线BC与AC关于y轴对称.
(1)求点A、B、C的坐标;
(2)若点P(m,2)在△ABC的内部(不包含边界),求m的取值范围;
(3)O为坐标原点,若过点O的直线将△ABC分成的两部分面积之比为1:2,求该直线的解析式.
10.如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
11.【模型建立】
如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA.
【模型应用】
(1)如图2,在图1中建立平面直角坐标系,使点E与坐标原点O重合,ED和EB所在直线分别为x轴、y轴,若OB=2,OC=1,请解答下列问题:
①点C的坐标是 ,点A的坐标是 ;
②在x轴上存在点M,使得以O,A,B,M为顶点的四边形的面积为4,请直接写出点M的坐标: ;
(2)如图3,已知直线l1:y=2x+4与x轴交于点A,与y轴交于点B,将直线l1绕点B旋转45°至直线l2,求直线l2的函数表达式.
12.在平面直角坐标系中,直线y=kx+8k(k是常数,且k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).
(1)求点A的坐标;
(2)将线段AB绕点A顺时针旋转90°到AD,作直线BD交x轴于点C,求直线BC的解析式;
(3)在(2)的条件下,如果动点P在x轴上运动,当△BDP的面积是△ABD面积的一半时,求出此时点P的坐标.
13.如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在y轴的正半轴上,点C在x轴的正半轴上,OA=8,OC=10.在OA边上取一点E,将纸片沿CE翻折,使点O落在AB边上的点D处.
(1)直接写出点D和点E的坐标:D( ),E( );
(2)求直线DE的表达式;
(3)若直线y=kx+b与DE平行,当它过长方形OABC的顶点C时,且与y轴相交于点F时,求△OCF的面积.
14.如图,在平面直角坐标系中,直线分别交x轴,y轴于A,B两点.已知点C(﹣2,0),作直线BC.
(1)求直线BC的函数表达式;
(2)若点D在直线BC上,且∠DAC=90°,求点D的坐标.
15.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象经过点A(0,2),B(﹣4,0),点C为直线AB上的一点,点C的纵坐标为3,点P是y轴上的一点.
(1)求点C的坐标;
(2)若点P的坐标为(0,4),求△PBC的面积;
(3)若∠BCP=45°,请直接写出点P的坐标.
参考答案
1.【解答】解:(1)∵OA=6,OB=10,四边形OACB为长方形,
∴C(6,10),
设此时直线DP解析式为y=kx+b,
把(0,2),C(6,10)分别代入,
得,
解得,
则此时直线DP解析式为yx+2;
(2)①当点P在线段AC上时,
OD=2,高为6,
∴S2×6=6,
当点P在线段BC上时,
OD=2,高为6+10﹣t=16﹣t,
∴S2×(16﹣t)=16﹣t,
综上:S;
②设P(m,10),则PB=PB'=m,
∵OB′=0B=10,OA=6,
∴AB'8,
∴B'C=10﹣8=2,
在Rt△B′PC中,
m2=22+(6﹣m)2,
解得m,
∴此时点P的坐标是(,10);
(3)存在,理由如下:
若△BDP为等腰三角形,分三种情况考虑:如图,
①当BD=BP1=OB﹣OD=10﹣2=8时,
在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得:CP12,
∴AP1=10﹣2,
即P1(6,10﹣2),
②当BP2=DP2时,此时P2在BD的中垂线上,
即P2(6,6),
③当DB=DP3=8时,
在Rt△DEP3中,DE=6,
根据勾股定理得:P3E2,
AP3=AE+EP3=22,
即P3(6,22),
综上,满足题意的P坐标为(6,6)或(6,22)或(6,10﹣2).
2.【解答】解:(1)∵直线l1:y=﹣x+5与直线l2交于点E.
当y=3时,3=﹣e+5,
e=2,
∴E(2,3),
∵直线l1:y=﹣x+5与x轴和y轴分别交于点A、点B,
∴令x=0,则y=5,令y=0,则x=5,
∴B(0,5),A(5,0),
∴OB=5,
∵,
∴OC=4,
∵点C在x轴的负半轴上,
∴C(﹣4,0)
把C(﹣4,0),E(2,3),代入l2:y=kx+b中得:
,
解得:,
∴直线l2的解析式;
(2)∵点F为线段EC上一个动点,过点F作FH⊥x轴于点H,交直线l1于点G,
设,则G(a,﹣a+5),H(a,0),
∴,
∵C(﹣4,0),
∴CH=a﹣(﹣4)=a+4,
∵,
∴,
解得:,
∴,
∴,
∵△FGE边FG上的高为:,
∴△FGE的面积;
(3)点M的坐标为或.理由如下:
由(1)知B(0,5),A(5,0),
OA=OB=5,
∴△AOB为等腰直角三角形,
∵将l2向右平移2个单位长度得到直线与y轴交于点Q,
∴,Q(0,1),
∴BQ=5﹣1=4,OQ=1,
当点M在直线l1右侧,∠MBA=∠BAQ时,
过点A作AF⊥x轴,交BM于点N,
∴AF∥y轴,
∴∠NAB=∠QBA,
在△NAB和△QBA中,
,
∴△NAB≌△QBA(ASA),
∴AN=BQ=4,
∴N(5,4),
设直线BM的解析式为y=kx+b,将B(0,5),N(5,4)代入得:
,
解得,
∴直线BM的解析式为,
∵直线BM和l3交于点M,联立得:,
,
∴;
当点M在直线l1左侧,∠MBA=∠BAQ时,BM交x轴于点F,
∵△AOB为等腰直角三角形,
∴∠ABO=∠OAB,
∴∠ABO﹣∠ABM=∠OAB﹣QAB,
即∠OAQ=∠OBF,
∵,
∴△AOQ≌△BOF(ASA),
∴OF=OQ=1,
∴F(1,0),
设直线BM的解析式为y=kx+b,将B(0,5),F(1,0)代入得:
,
解得,
∴直线BM的解析式为y=﹣5x+5,
∵直线BM和l3交于点M,联立得:,
,
∴.
综上所述,点M的坐标为或.
3.【解答】解:(1)∵直线y2=x+2过点C(3,a),
∴a=3+2=5,
由题意得,,
∴,
∴直线y1的解析式为:yx+6;
(2)设点D(a,0),则E(a,a+6),F(a,a+2),
由EF=4得,
|(a+2)﹣(a+6)|=4,
∴a=0(舍去)或a=6,
∴D(6,0);
(3)设点D(a,0),则E(a,a+6),F(a,a+2),
∵四边形EFHM是矩形,
∴yM=yF=a+2,yH=yEa+6,
由x+2a+6得,
xa+4,
∴xM=xHa+4,
由得,
y=﹣3x+14,
∴点M在直线y=﹣3x+14上运动.
4.【解答】解:(1)在yx+8中,令x=0得y=8,令y=0得x=﹣6,
∴A(﹣6,0),B(0,8),
∴AB10;
在y=kx+5中,令x=0得y=5,
∴C(0,5),
∵OC=OD,
∴D(5,0),
把D(5,0)代入y=kx+5得:5k+5=0,
解得k=﹣1,
∴k的值为﹣1,线段AB的长为10;
(2)①过F作FK∥CD交x轴于K,连接CK,如图:
设F(m,m+8),直线FK解析式为y=﹣x+t,
∴﹣m+tm+8,
解得tm+8,
∴直线FK解析式为y=﹣xm+8,
令y=0得xm+8,
∴K(m+8,0),
∴DK=5﹣(m+8)m﹣3,
∵FK∥CD,
∴S△CDF=S△CDK=10,
∴(m﹣3)×5=10,
解得m=﹣3,
∴F(﹣3,4);
②如图:
当△ODG≌△GFO时,OD=GF,GD=OF,
∴四边形DOFG是平行四边形,
∴FD的中点与OG的中点重合,
设F(p,p+8),G(q,﹣q+5),
∵O(0,0),D(5,0),
∴,
解得,
∴p+8()+8,
∴F的坐标为(,).
5.【解答】解:(1)∵△OAB为直角三角形,AB=10,OA=8,
∴82+OB2=102,
解得OB=6,
即B点坐标为(6,0),
将A(0,8),B(6,0)两点坐标分别代入y=ax+b,
得,
解得,
故直线AB的解析式为.
(2)由条件可知BD=AB=10,
∴OD=OB+BD=16.
∵点D在x轴的正半轴上,
∴点D的坐标为D(16,0).
设点C的坐标为C(0,y)(y<0),由题意可知CD=AC,CD2=AC2.
在Rt△OCD中,由勾股定理得162+y2=(8﹣y)2,解得y=﹣12.
∴点C的坐标为C(0,﹣12).
设直线CD的解析式为y=kx﹣12(k≠0).
∴16k﹣12=0,解得.
∴直线CD的解析式为.
(3)当AB⊥BD时,由题意得点D在第一象限,如图,
过D作DF⊥x轴于点F,
∴∠AOB=∠BFD=90°,
∴∠ABO=∠BDF,
∵以BC为对称轴作△ABC的轴对称图形为△DBC,
∴AB=DB,
在△AOB和△BFD中,
,
∴△AOB≌△BFD(AAS),
∴BF=AO=8,DF=BO=6,
∴OF=OB+BF=14,
∴D(14,6).
设直线AD与BC交点为E,点E为AD中点,
则E点坐标为(7,7).
设直线BE的解析式为y=mx+n,
将点B(6,0),E(7,7)分别代入直线方程,
得,
解得,
故直线BE的解析式为y=7x﹣42,
上式中,令x=0,则y=﹣42,
则C点坐标为(0,﹣42).
6.【解答】解:(1)①若点P的坐标为(0,3),则点Q的坐标为(3,0),
故答案为:(0,3);
②若点Q的坐标为(2,﹣1),
同理可得:点P的坐标为(1,2),
故答案为:(1,2);
(2)①当点E落在x轴上时,如图,
则CD⊥x轴,
x=﹣2时,y=﹣2x+4=4+4=8,
故点D(﹣2,8);
②当点E落在y轴时,如图:
设点D(m,﹣2m+4),
点D的“链垂点E在y轴上,
过点D作DH⊥x轴于点H,
∴∠DHC=∠COE=90°,
∴∠CDH+∠DCH=90°,
∵∠DCE=∠ECH+∠DCH=90°,
∴∠CDH=∠ECH,
由旋转得CD=EC,
∴△CHD≌△EOC(AAS),
则DH=OC=2,即:﹣2m+4=2,解得:m=1,
故点D(1,2),
综上,点D(﹣2,8)或(1,2);
(3)①如图,过点B作BH⊥x轴于点H,过点A作AG⊥x轴于点G,
则∠AGC=∠CHB,∠ACG=∠CBH,AC=CB,
∴△CHB≌△EOC(AAS),
设点C的坐标为(n,0),
∴GC=HB=n+1,GA=HC=2,
∴点B(n+2,n+1),
∴BO+BA,相当于在直线y=x上寻找一点P(n,n),使得点P到N(﹣2,﹣1),到M(﹣3,1)的距离和最小,
作N关于直线y=x的对称点N′(﹣1,﹣2),连接PN′,MN′,
∴PM+PN=PM+PN′≥NM′,
∴MN′的最小值为,
∴BO+BA的最小值为;
②设直线MN的解析式为y=kx+b,
∵N′(﹣1,﹣2),M(﹣3,1),
∴,解得,
∴直线MN的解析式为yx,
联立y=x解得x,
∴n,
∴当BO+BA最小时点C的坐标为(,0).
7.【解答】解:(1)∵C(0,﹣6)在直线CD上,
∴﹣6=b,
∴CD:y=kx﹣6,
∵D点横坐标为4,
∴D(4,6),
∵D在直线CD上,
∴6=4k﹣6,
∴k=3,
∴CD的解析式为:y=3x﹣6;
(2)①∵△BDP和△BCP等高,且△BDP面积等于△BCP面积的一半,
∴CP=2DP,
∴m﹣0=2(4﹣m),
∴m;
②存在最小值,
连接BD′,如图:
由对称的性质可知,BD=BD′,
∴D′在以B为圆心,BD为半径的圆上,
∴当B,E,D′共线时存在最值,
∵直线分别与x轴、y轴相交于点A、B,
∴B(0,3),
∴BD5,
∵E为直线CD与x轴的交点,
∴E(2,0),
∴BE,
∴D′E的最小值为:5;
当P与C重合时,D和D3关于y轴对称,
∴D3(﹣4,6),
设直线BE的解析式为:y=tx+3,
则0=2t+3,
∴t,
设D2(x,x+3),
∴D2B=BD=5,即5,
∴x4,
∴当P在线段CD上时,取不到D2,
又∵P不与C,D重合,
∴D3也取不到,
∴D′E没有最大值,
综上所述,D′E有最小值5;
(3)∵点P在直线CD上,
∴n=3m﹣6,
∴直线y=mx+2n﹣21=mx+6m﹣12﹣21=(x+6)m﹣33,
∴直线y=mx+2n﹣21恒过点(﹣6,﹣33),
∵BP=PQ,B,P,Q共线,
∴P是BQ的中点,
∴Q(2m,6m﹣15),
当直线y=mx+2n﹣21过点B时,3=6m﹣33,
∴m=6,
当直线y=mx+2n﹣21过点D时,6=4m+6m﹣33,
∴m=3.9,
∵P在线段CD上,
∴0<m<4,
∴当3.9≤m<4时,直线y=mx+2n﹣21与BD有交点,
∴点Q在直线y=mx+2n﹣21下方,
当0<m<3.9时,直线y=mx+2n﹣21与BQ和DQ有交点,
∴点Q在直线y=mx+2n﹣21下方,
∴2m2+6m﹣33>6m﹣15,
解得:m>3或m<﹣3,
∴3<m<4.
8.【解答】解:(1)在yx+12中,令x=0,则y=12,令y=0,则x=9,
∴点A(9,0),B(0,12),
∴OA=9,OB=12,
在Rt△AOB中,由勾股定理得:AB15,
由折叠的性质可知,AD=AB=15,
∴OD=OA+AD=9+15=24,
∴点D的坐标是(24,0),
设OC=x,则BC=OB+OC=12+x,
由折叠的性质可知,CD=BC=12+x,
在Rt△COD中,由勾股定理得:OC2+OD2=CD2,
∴x2+242=(x+12)2,
解得:x=18,即OC=18,
∴点C的坐标为(0,﹣18);
设直线CD的解析式为y=kx+b,
∴,
∴,
∴直线CD的表达式为:yx﹣18;
(2)∵C(0,﹣18),D(24,0),
∴OC=18,OD=24,
则S△COD18×9=135,
则S△MAB,
∵点M是y轴上一动点,
∴设点M的坐标为(0,m),
∴BM=|m﹣12|,
则S△MABBM OA|m﹣12|×9,
∴m=27或﹣3,
∴点M的坐标为(0,27)或(0,﹣3);
(3)在第一象限内存在点P,使△PAB为等腰直角三角形;理由如下:
①当∠BAP=90°,AB=AP,则△PAB为等腰直角三角形,
如图1,过点P作PG⊥x轴于点G,
∴∠PGA=∠AOB=90°,
∵∠BAP=90°,
∴∠BAO+∠PAG=90°,
∵∠ABO+∠BAO=90°,
∴∠ABO=∠PAG,
在△AOB和△PGA中,∠ABO=∠PAG,∠AOB=∠PGA,AB=PA,
∴△AOB≌△PGA(AAS),
∴OA=PG=9,OB=AG=12,
∴OG=OA+AG=21,
∴点P的坐标为(21,9);
②当∠ABP=90°,BA=BP,则△PAB为等腰直角三角形,
如图2,过点P作PH⊥y轴于点H,
同理 可证,△AOB≌△BHP(AAS),
∴OA=BH=9,PH=OB=12,
∴OH=OB+BH=21,
∴点P的坐标为(12,21);
③当∠APB=90°,PA=PB,则△PAB为等腰直角三角形,
如图3,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PNB=∠PMA=∠MPN=90°,
∴∠APN+∠APM=90°,
∵∠APB=90°,
∴∠BPN+∠APN=90°,
∴∠APM=∠BPN,
在△APM和△BPN中,∠APM=∠BPN,PA=PB,∠PMA=∠PNB,
∴△APM≌△BPN(ASA),
∴AM=BN,PM=PN,
∴设点P的坐标为(p,p),
∴OM=ON=p,
∴BN=OB﹣ON=12﹣p,AM=OM﹣OA=p﹣9,
∴12﹣p=p﹣9,
解得:p,则点P的坐标为(,),
综上可知,第一象限内存在点P,使△PAB为等腰直角三角形,点P的坐标(21,9)或(12,21)或(,).
9.【解答】解:(1)在y=x+3中,令x=0得y=3,令y=0得x=﹣3,
∴A(﹣3,0),C(0,3),
∵直线BC与直线AC关于y轴对称,
∴点B与点A关于y轴对称,
∴B(3,0);
(2)设直线BC的解析式为y=kx+b,把点C(0,3)和点B(3,0)的坐标代入得:
,解得:,
∴直线BC的解析式为y=﹣x+3;
当点P在直线CA上时,m+3=2,
解得m=﹣1,
当点P在直线BC上时,﹣m+3=2,
解得m=1,
∴当点P在△ABC的内部时,m的取值范围是﹣1<m<1;
(3)∵A(﹣3,0),C(0,3),B(3,0),
∴S△ABC=×6×3=9;
①设直线L交AC于K,S△AOK:S四边形KOBC=1:2,过K作KH⊥AB于H,如图:
∴S△AOKS△ABC=3,
∴3×HK=3,
则KH=2,
在y=x+3中,令y=2,
即2=x+3,
解得:x=﹣1,
∴K(﹣1,2)
设直线L解析式为y=px,
∴2=﹣p,
解得p=﹣2,
∴直线L解析式为y=﹣2x;
②设直线L交BC于T,S△BOT:S四边形AOTC=1:2,过T作TH'⊥AB于H',如图:
同理可得:3×TH′=3,
解得:TH′=2,
在y=﹣x+3中,令y=2得x=1,
则点T(1,2),
则直线L解析式为y=2x;
综上所述,直线L的解析式为y=﹣2x或y=2x.
10.【解答】解:(1)对于yx,令x=0,则y,令y=0,解得x=﹣2,
故点A、B的坐标分别为(﹣2,0)、(0,);
(2)①设直线AP交y轴于点H,
设直线AP的表达式为:y=k(x+2),
当x=0时,y=2k,当x=2时,y=4k,
即点H、P的坐标分别为(0,2k),(2,4k),
则△ABP的面积=S△HBP+S△HBAAC BH4(2k),
解得:k,
∴点P的坐标为(2,);
当点P在点D的上方时,根据对称性可知P(2,),
综上所述,点P的坐标为(2,)或(2,),
②由(1)(2)知,P(2,),A(﹣2,0),B(0,),设点Q(s,t),
∵点A、B、P、Q为顶点的四边形是平行四边形,
∴①Ⅰ、以AP为对角线,由中点坐标公式得,
∴,
∴点Q(0,﹣3),
Ⅱ、以AB为对角线,由中点坐标公式得,
∴,
∴点Q(﹣4,3);
Ⅲ、以AQ为对角线,由中点坐标公式得,
∴,
∴Q(4,0),
综上所述,以点A、B、P、Q为顶点的四边形是平行四边形,点Q坐标为(0,﹣3)或(﹣4,3)或(4,0).
11.【解答】【模型建立】证明:∵AD⊥ED,BE⊥ED,
∴∠BEC=∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠BCE=∠CAD,
在△BEC和△CDA中,
,
∴△BEC≌△CDA(AAS);
(1)解:①∵OC=1,
∴点C的坐标是(1,0),
由【模型建立】得△BOC≌△CDA,
∴AD=OC=1,CD=OB=2,
∴OD=OC+CD=3,
∴点A的坐标是(3,1);
故答案为:(1,0),(3,1);
②如图2,当M在x轴正半轴时,连接OA,
∵点A的坐标是(3,1),OB=2,
S△AOB2×3=3,
∴S△OAM=S四边形﹣S△AOB=4﹣3=1,
∴OM×1=1,
OM=2,
∴M(2,0),
如图2.2,当M在x轴负半轴时,连接OA,
∵点A的坐标是(3,1),OB=2,
S△AOB2×3=3,
∴S△OBM=S四边形﹣S△AOB=4﹣3=1,
∴OM OB=1,
∴OM=1,
∴M(﹣1,0),
故答案为:(2,0)或(﹣1,0);
(2)解:过点B作BF⊥l2于点F,
∵将直线l1绕点A逆时针旋转45°至直线l2,
∴△ABF是等腰直角三角形,
∵直线l1:y=2x+4与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴AB2,
∴AF=BFAB,
设l2的函数解析式为y=kx+4,则F(a,ka+4),依题意得:
,
解得:或,
∴直线l2的函数解析式为yx+4或y=﹣3x+4.
12.【解答】解:(1)将点B的坐标(0,6)代入解析式y=kx+8k,
得8k=6,
解得,
∴,
当y=0时,,
解得x=﹣8,
∴点A的坐标为(﹣8,0);
(2)过点D作DE⊥x轴于点E,∠DEA=90°,
由旋转可知,AB=AD,∠BAD=90°,
∴∠BAO+∠DAO=90°,
又∵∠BAO+∠ABO=90°,
∴∠DAE=∠ABO,
在△AOB和△DEA中,
,
∴△AOB≌△DEA(AAS),
∴AE=OB=6,DE=OA=8,
∴OE=AO﹣AE=2,
∴D(﹣2,﹣8),
设直线BC的解析式为y=ax+b,
,
解得,
∴直线BC的解析式为y=7x+6;
(3)在Rt△AOB中,,
∵△AOB≌△DEA(AAS),
∴AD=AB=10,
∴,
对于y=7x+6,
当y=0时,7x+6=0,
∴,
则点C的坐标是,
设点P的坐标为(m,0),则,
则,
∵△BDP的面积是△ABD面积的一半,
∴,
∴,或,
∴点P的坐标为或.
13.【解答】解:(1)依题意可知,折痕CE是四边形OCAB的对称轴,
在Rt△CBD中,OC=CD=10,BC=OA=8,
由勾股定理,得BD6,
∴AD=BA﹣BD=10﹣6=4,
∴D(4,8).
在Rt△DAE中,由勾股定理,得AE2+AD2=DE2,
又DE=OE,AE=8﹣OE,
(8﹣OE)2+42=OE2,
解得OE=5,
∴E(0,5).
∴E(0,5),D(4,8);
故答案为:4,8;0,5;
(2)设D、E两点所在的直线的解析式为y=kx+b,
则,解得,
所以过D、E两点的直线函数表达式为yx+5.
(3)∵直线y=kx+b与DE平行,
∴k,
∵直线过长方形OABC的顶点C(10,0),
∴,
∴b,
∴直线CF的解析式为y,
∴x=0时,y,
∴F(0,),
∴OF,
∴△OCF的面积.
14.【解答】解:(1)对于,当x=0时,y=4,当y=0时,x=3,
即点A、B的坐标分别为:(3,0)、(0,4),
设直线BC的表达式为:y=kx+4,
将点C的坐标代入上式得:0=﹣2k+4,则k=2,
则直线BC的表达式为:y=2x+4;
(2)当∠DAC=90°时,则点A、D的横坐标相同,
当x=3时,y=2x+4=10,
即点D(3,10).
15.【解答】解:(1)把A(0,2),B(﹣4,0)代入y=kx+b得:
,
解得,
∴直线AB解析式为yx+2,
令y=3得3x+2,
解得x=2,
∴C的坐标为(2,3);
(2)如图:
∵P(0,4),A(0,2),
∴PA=2,
∵C(2,3),B(﹣4,0),
∴S△APC2×2=2,S△APB2×4=4,
∴S△PBC=2+4=6,
∴△PBC的面积为6;
(3)过B作BH⊥CP交CP延长线于H,过H作MN∥x轴,过B过BN⊥MN于N,过C作CM⊥MN于M,
设H(m,n),
当P在BC上方时,如图:
∵∠BCP=45°,BH⊥CP,
∴△BCH是等腰直角三角形,∠BHC=90°,
∴BH=CH,∠BHN=90°﹣∠MHC=∠MCH,
∵∠N=∠M=90°,
∴△BHN≌△HCM(AAS),
∴BN=HM,NH=CM,
∵B(﹣4,0),C(2,3),
∴,
解得,
∴H(﹣2.5,4.5),
由H(﹣2.5,4.5),C(2,3)得直线CH解析式为yx,
令x=0得y;
∴P(0,);
当P在BC下方时,如图:
同理可得BN=MH,NH=CM,
∴,
解得,
∴H(,),
由H(,),C(2,3)可得CP解析式为y=3x﹣3,
令x=0得y=﹣3,
∴P(0,﹣3);
综上所述,P的坐标为P(0,)或(0,﹣3).
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练一次函数与几何综合压轴题练习
1.综合与探究:
如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知 OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB 的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD 的面积S关于t的函数解析式;
②把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP 为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2.如图1,在平面直角坐标系中,直线l1:y=﹣x+5与x轴和y轴分别交于点A、点B,直线l2:y=kx+b与x轴、y轴分别交于点C和点D,且,直线l1与直线l2交于点E(e,3).
(1)求直线l2的解析式;
(2)若点F为线段EC上一个动点,过点F作FH⊥x轴于点H,交直线l1于点G,当时,求点F的坐标及△FGE的面积;
(3)如图2,将l2向右平移2个单位长度得到直线l3,直线l3与y轴交于点Q,点M为l3上一动点,当∠MBA=∠BAQ时,请写出所有满足条件的点M的坐标,并写出求其中一个点M坐标的过程.
3.如图,在平面直角坐标系xOy中,直线y1=mx+n(m≠0)与x轴交于点A,与y轴交于点B(0,6),直线y2=x+2与y轴交于点P,与y1交于点C(3,a).点D为x轴上正半轴一动点,过点D作x轴的垂线与直线y1,y2分别相交于E,F两点,过点E作EH∥x轴的直线交y2于点H.
(1)求a的值及y1的函数表达式;
(2)当EF=4,求D点的坐标;
(3)以EF,EH为边作长方形EFMH,当点D在运动过程中,试探究M的运动轨迹是否为一条直线中的一部分?若是,直接写出该直线解析式;若不是,请说明理由.
4.如图,在平面直角坐标系中,直线分别交x轴、y轴于A,B两点,直线y=kx+5分别交x轴、y轴的正半轴于D,C两点,OC=OD,两直线相交于点E.
(1)求k的值与线段AB的长;
(2)若F为线段AE上的动点,
①连接FC,FD,S△CDF=10时,求点F的坐标;
②G为线段DE上的动点,当△ODG≌△GFO时,求点F的坐标.
5.如图,在平面直角坐标系xOy中,直线AB:y=ax+b(a<0)与y轴、x轴分别交于点A(0,8),B,AB的长为10,点C在y轴的负半轴上,以BC为对称轴作△ABC的轴对称图形,点A的对称点为点D.
(1)求直线AB的解析式;
(2)若点D恰好落在x轴正半轴上,求点D的坐标以及直线CD的解析式;
(3)当AB⊥BD时,直接写出点C的坐标.
6.平面直角坐标系xOy中有点A和点P,若将点P绕点A顺时针旋转90°后得到点Q,则称点Q为点P关于点A的“链垂点”,图1为点P关于点A的“链垂点”Q的示意图.
(1)如图2,已知点A的坐标为(0,0),点P关于点A的“链垂点”为点Q.
①若点P的坐标为(0,3),则点Q的坐标为 ;
②若点Q的坐标为(2,﹣1),则点P的坐标为 ;
(2)已知点C的坐标为(﹣2,0),点D在直线y=﹣2x+4上,若点D关于点C的“链垂点”E在坐标轴上,试求出点D的坐标;
(3)在平面直角坐标系xOy中,已知点A(﹣1,2),点C是x轴上的动点,点A关于点C的“链垂点”是点B,连接BO、BA.
①直接写出BO+BA的最小值;
②直接写出当BO+BA最小时点C的坐标.
7.如图,在平面直角坐标系xOy中,直线分别与x轴、y轴相交于点A、B,且与经过点C(0.﹣6)直线y=kx+b(k≠0)相交于点D.点D的横坐标为4,直线CD与x轴相交于点E.点P(m,n)是线段CD上一点(不含端点),连接BP.
(1)求直线CD的函数表达式;
(2)①若△BDP面积等于△BCP面积的一半,求m的值;
②点D′是点D关于直线BP对称点,连接D′E.当点P在线段CD上运动时,D′E是否存在最大值或最小值?若存在,请直接写出D′E的最值;若不存在,请说明理由;
(3)延长BP至Q,使PQ=BP,连接DQ.若直线y=mx+2n﹣21与△BDQ的边有两个交点,求m的取值范围.
8.如图,在平面直角坐标系中,直线AB:yx+12与x轴、y轴分别交于点A、B,点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处.
(1)求C点的坐标以及直线CD的解析式;
(2)点M是y轴上一动点,若S△MAB,求出点M的坐标;
(3)在第一象限内是否存在点P,使△PAB为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
9.如图,直线y=x+3与坐标轴分别交于点A,C,直线BC与AC关于y轴对称.
(1)求点A、B、C的坐标;
(2)若点P(m,2)在△ABC的内部(不包含边界),求m的取值范围;
(3)O为坐标原点,若过点O的直线将△ABC分成的两部分面积之比为1:2,求该直线的解析式.
10.如图,直线与坐标轴交于A、B两点,点C与点A关于y轴对称.CD⊥x轴与直线AB交于点D.
(1)求点A和点B的坐标;
(2)点P在直线CD上,且△ABP的面积为,
①求出点P的坐标;
②点Q为平面内一点,当点P在直线AB下方时,以点A、B、P、Q为顶点的四边形是平行四边形,请直接写出所有符合要求的点Q坐标.
11.【模型建立】
如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA.
【模型应用】
(1)如图2,在图1中建立平面直角坐标系,使点E与坐标原点O重合,ED和EB所在直线分别为x轴、y轴,若OB=2,OC=1,请解答下列问题:
①点C的坐标是 ,点A的坐标是 ;
②在x轴上存在点M,使得以O,A,B,M为顶点的四边形的面积为4,请直接写出点M的坐标: ;
(2)如图3,已知直线l1:y=2x+4与x轴交于点A,与y轴交于点B,将直线l1绕点B旋转45°至直线l2,求直线l2的函数表达式.
12.在平面直角坐标系中,直线y=kx+8k(k是常数,且k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).
(1)求点A的坐标;
(2)将线段AB绕点A顺时针旋转90°到AD,作直线BD交x轴于点C,求直线BC的解析式;
(3)在(2)的条件下,如果动点P在x轴上运动,当△BDP的面积是△ABD面积的一半时,求出此时点P的坐标.
13.如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在y轴的正半轴上,点C在x轴的正半轴上,OA=8,OC=10.在OA边上取一点E,将纸片沿CE翻折,使点O落在AB边上的点D处.
(1)直接写出点D和点E的坐标:D( ),E( );
(2)求直线DE的表达式;
(3)若直线y=kx+b与DE平行,当它过长方形OABC的顶点C时,且与y轴相交于点F时,求△OCF的面积.
14.如图,在平面直角坐标系中,直线分别交x轴,y轴于A,B两点.已知点C(﹣2,0),作直线BC.
(1)求直线BC的函数表达式;
(2)若点D在直线BC上,且∠DAC=90°,求点D的坐标.
15.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象经过点A(0,2),B(﹣4,0),点C为直线AB上的一点,点C的纵坐标为3,点P是y轴上的一点.
(1)求点C的坐标;
(2)若点P的坐标为(0,4),求△PBC的面积;
(3)若∠BCP=45°,请直接写出点P的坐标.
参考答案
1.【解答】解:(1)∵OA=6,OB=10,四边形OACB为长方形,
∴C(6,10),
设此时直线DP解析式为y=kx+b,
把(0,2),C(6,10)分别代入,
得,
解得,
则此时直线DP解析式为yx+2;
(2)①当点P在线段AC上时,
OD=2,高为6,
∴S2×6=6,
当点P在线段BC上时,
OD=2,高为6+10﹣t=16﹣t,
∴S2×(16﹣t)=16﹣t,
综上:S;
②设P(m,10),则PB=PB'=m,
∵OB′=0B=10,OA=6,
∴AB'8,
∴B'C=10﹣8=2,
在Rt△B′PC中,
m2=22+(6﹣m)2,
解得m,
∴此时点P的坐标是(,10);
(3)存在,理由如下:
若△BDP为等腰三角形,分三种情况考虑:如图,
①当BD=BP1=OB﹣OD=10﹣2=8时,
在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得:CP12,
∴AP1=10﹣2,
即P1(6,10﹣2),
②当BP2=DP2时,此时P2在BD的中垂线上,
即P2(6,6),
③当DB=DP3=8时,
在Rt△DEP3中,DE=6,
根据勾股定理得:P3E2,
AP3=AE+EP3=22,
即P3(6,22),
综上,满足题意的P坐标为(6,6)或(6,22)或(6,10﹣2).
2.【解答】解:(1)∵直线l1:y=﹣x+5与直线l2交于点E.
当y=3时,3=﹣e+5,
e=2,
∴E(2,3),
∵直线l1:y=﹣x+5与x轴和y轴分别交于点A、点B,
∴令x=0,则y=5,令y=0,则x=5,
∴B(0,5),A(5,0),
∴OB=5,
∵,
∴OC=4,
∵点C在x轴的负半轴上,
∴C(﹣4,0)
把C(﹣4,0),E(2,3),代入l2:y=kx+b中得:
,
解得:,
∴直线l2的解析式;
(2)∵点F为线段EC上一个动点,过点F作FH⊥x轴于点H,交直线l1于点G,
设,则G(a,﹣a+5),H(a,0),
∴,
∵C(﹣4,0),
∴CH=a﹣(﹣4)=a+4,
∵,
∴,
解得:,
∴,
∴,
∵△FGE边FG上的高为:,
∴△FGE的面积;
(3)点M的坐标为或.理由如下:
由(1)知B(0,5),A(5,0),
OA=OB=5,
∴△AOB为等腰直角三角形,
∵将l2向右平移2个单位长度得到直线与y轴交于点Q,
∴,Q(0,1),
∴BQ=5﹣1=4,OQ=1,
当点M在直线l1右侧,∠MBA=∠BAQ时,
过点A作AF⊥x轴,交BM于点N,
∴AF∥y轴,
∴∠NAB=∠QBA,
在△NAB和△QBA中,
,
∴△NAB≌△QBA(ASA),
∴AN=BQ=4,
∴N(5,4),
设直线BM的解析式为y=kx+b,将B(0,5),N(5,4)代入得:
,
解得,
∴直线BM的解析式为,
∵直线BM和l3交于点M,联立得:,
,
∴;
当点M在直线l1左侧,∠MBA=∠BAQ时,BM交x轴于点F,
∵△AOB为等腰直角三角形,
∴∠ABO=∠OAB,
∴∠ABO﹣∠ABM=∠OAB﹣QAB,
即∠OAQ=∠OBF,
∵,
∴△AOQ≌△BOF(ASA),
∴OF=OQ=1,
∴F(1,0),
设直线BM的解析式为y=kx+b,将B(0,5),F(1,0)代入得:
,
解得,
∴直线BM的解析式为y=﹣5x+5,
∵直线BM和l3交于点M,联立得:,
,
∴.
综上所述,点M的坐标为或.
3.【解答】解:(1)∵直线y2=x+2过点C(3,a),
∴a=3+2=5,
由题意得,,
∴,
∴直线y1的解析式为:yx+6;
(2)设点D(a,0),则E(a,a+6),F(a,a+2),
由EF=4得,
|(a+2)﹣(a+6)|=4,
∴a=0(舍去)或a=6,
∴D(6,0);
(3)设点D(a,0),则E(a,a+6),F(a,a+2),
∵四边形EFHM是矩形,
∴yM=yF=a+2,yH=yEa+6,
由x+2a+6得,
xa+4,
∴xM=xHa+4,
由得,
y=﹣3x+14,
∴点M在直线y=﹣3x+14上运动.
4.【解答】解:(1)在yx+8中,令x=0得y=8,令y=0得x=﹣6,
∴A(﹣6,0),B(0,8),
∴AB10;
在y=kx+5中,令x=0得y=5,
∴C(0,5),
∵OC=OD,
∴D(5,0),
把D(5,0)代入y=kx+5得:5k+5=0,
解得k=﹣1,
∴k的值为﹣1,线段AB的长为10;
(2)①过F作FK∥CD交x轴于K,连接CK,如图:
设F(m,m+8),直线FK解析式为y=﹣x+t,
∴﹣m+tm+8,
解得tm+8,
∴直线FK解析式为y=﹣xm+8,
令y=0得xm+8,
∴K(m+8,0),
∴DK=5﹣(m+8)m﹣3,
∵FK∥CD,
∴S△CDF=S△CDK=10,
∴(m﹣3)×5=10,
解得m=﹣3,
∴F(﹣3,4);
②如图:
当△ODG≌△GFO时,OD=GF,GD=OF,
∴四边形DOFG是平行四边形,
∴FD的中点与OG的中点重合,
设F(p,p+8),G(q,﹣q+5),
∵O(0,0),D(5,0),
∴,
解得,
∴p+8()+8,
∴F的坐标为(,).
5.【解答】解:(1)∵△OAB为直角三角形,AB=10,OA=8,
∴82+OB2=102,
解得OB=6,
即B点坐标为(6,0),
将A(0,8),B(6,0)两点坐标分别代入y=ax+b,
得,
解得,
故直线AB的解析式为.
(2)由条件可知BD=AB=10,
∴OD=OB+BD=16.
∵点D在x轴的正半轴上,
∴点D的坐标为D(16,0).
设点C的坐标为C(0,y)(y<0),由题意可知CD=AC,CD2=AC2.
在Rt△OCD中,由勾股定理得162+y2=(8﹣y)2,解得y=﹣12.
∴点C的坐标为C(0,﹣12).
设直线CD的解析式为y=kx﹣12(k≠0).
∴16k﹣12=0,解得.
∴直线CD的解析式为.
(3)当AB⊥BD时,由题意得点D在第一象限,如图,
过D作DF⊥x轴于点F,
∴∠AOB=∠BFD=90°,
∴∠ABO=∠BDF,
∵以BC为对称轴作△ABC的轴对称图形为△DBC,
∴AB=DB,
在△AOB和△BFD中,
,
∴△AOB≌△BFD(AAS),
∴BF=AO=8,DF=BO=6,
∴OF=OB+BF=14,
∴D(14,6).
设直线AD与BC交点为E,点E为AD中点,
则E点坐标为(7,7).
设直线BE的解析式为y=mx+n,
将点B(6,0),E(7,7)分别代入直线方程,
得,
解得,
故直线BE的解析式为y=7x﹣42,
上式中,令x=0,则y=﹣42,
则C点坐标为(0,﹣42).
6.【解答】解:(1)①若点P的坐标为(0,3),则点Q的坐标为(3,0),
故答案为:(0,3);
②若点Q的坐标为(2,﹣1),
同理可得:点P的坐标为(1,2),
故答案为:(1,2);
(2)①当点E落在x轴上时,如图,
则CD⊥x轴,
x=﹣2时,y=﹣2x+4=4+4=8,
故点D(﹣2,8);
②当点E落在y轴时,如图:
设点D(m,﹣2m+4),
点D的“链垂点E在y轴上,
过点D作DH⊥x轴于点H,
∴∠DHC=∠COE=90°,
∴∠CDH+∠DCH=90°,
∵∠DCE=∠ECH+∠DCH=90°,
∴∠CDH=∠ECH,
由旋转得CD=EC,
∴△CHD≌△EOC(AAS),
则DH=OC=2,即:﹣2m+4=2,解得:m=1,
故点D(1,2),
综上,点D(﹣2,8)或(1,2);
(3)①如图,过点B作BH⊥x轴于点H,过点A作AG⊥x轴于点G,
则∠AGC=∠CHB,∠ACG=∠CBH,AC=CB,
∴△CHB≌△EOC(AAS),
设点C的坐标为(n,0),
∴GC=HB=n+1,GA=HC=2,
∴点B(n+2,n+1),
∴BO+BA,相当于在直线y=x上寻找一点P(n,n),使得点P到N(﹣2,﹣1),到M(﹣3,1)的距离和最小,
作N关于直线y=x的对称点N′(﹣1,﹣2),连接PN′,MN′,
∴PM+PN=PM+PN′≥NM′,
∴MN′的最小值为,
∴BO+BA的最小值为;
②设直线MN的解析式为y=kx+b,
∵N′(﹣1,﹣2),M(﹣3,1),
∴,解得,
∴直线MN的解析式为yx,
联立y=x解得x,
∴n,
∴当BO+BA最小时点C的坐标为(,0).
7.【解答】解:(1)∵C(0,﹣6)在直线CD上,
∴﹣6=b,
∴CD:y=kx﹣6,
∵D点横坐标为4,
∴D(4,6),
∵D在直线CD上,
∴6=4k﹣6,
∴k=3,
∴CD的解析式为:y=3x﹣6;
(2)①∵△BDP和△BCP等高,且△BDP面积等于△BCP面积的一半,
∴CP=2DP,
∴m﹣0=2(4﹣m),
∴m;
②存在最小值,
连接BD′,如图:
由对称的性质可知,BD=BD′,
∴D′在以B为圆心,BD为半径的圆上,
∴当B,E,D′共线时存在最值,
∵直线分别与x轴、y轴相交于点A、B,
∴B(0,3),
∴BD5,
∵E为直线CD与x轴的交点,
∴E(2,0),
∴BE,
∴D′E的最小值为:5;
当P与C重合时,D和D3关于y轴对称,
∴D3(﹣4,6),
设直线BE的解析式为:y=tx+3,
则0=2t+3,
∴t,
设D2(x,x+3),
∴D2B=BD=5,即5,
∴x4,
∴当P在线段CD上时,取不到D2,
又∵P不与C,D重合,
∴D3也取不到,
∴D′E没有最大值,
综上所述,D′E有最小值5;
(3)∵点P在直线CD上,
∴n=3m﹣6,
∴直线y=mx+2n﹣21=mx+6m﹣12﹣21=(x+6)m﹣33,
∴直线y=mx+2n﹣21恒过点(﹣6,﹣33),
∵BP=PQ,B,P,Q共线,
∴P是BQ的中点,
∴Q(2m,6m﹣15),
当直线y=mx+2n﹣21过点B时,3=6m﹣33,
∴m=6,
当直线y=mx+2n﹣21过点D时,6=4m+6m﹣33,
∴m=3.9,
∵P在线段CD上,
∴0<m<4,
∴当3.9≤m<4时,直线y=mx+2n﹣21与BD有交点,
∴点Q在直线y=mx+2n﹣21下方,
当0<m<3.9时,直线y=mx+2n﹣21与BQ和DQ有交点,
∴点Q在直线y=mx+2n﹣21下方,
∴2m2+6m﹣33>6m﹣15,
解得:m>3或m<﹣3,
∴3<m<4.
8.【解答】解:(1)在yx+12中,令x=0,则y=12,令y=0,则x=9,
∴点A(9,0),B(0,12),
∴OA=9,OB=12,
在Rt△AOB中,由勾股定理得:AB15,
由折叠的性质可知,AD=AB=15,
∴OD=OA+AD=9+15=24,
∴点D的坐标是(24,0),
设OC=x,则BC=OB+OC=12+x,
由折叠的性质可知,CD=BC=12+x,
在Rt△COD中,由勾股定理得:OC2+OD2=CD2,
∴x2+242=(x+12)2,
解得:x=18,即OC=18,
∴点C的坐标为(0,﹣18);
设直线CD的解析式为y=kx+b,
∴,
∴,
∴直线CD的表达式为:yx﹣18;
(2)∵C(0,﹣18),D(24,0),
∴OC=18,OD=24,
则S△COD18×9=135,
则S△MAB,
∵点M是y轴上一动点,
∴设点M的坐标为(0,m),
∴BM=|m﹣12|,
则S△MABBM OA|m﹣12|×9,
∴m=27或﹣3,
∴点M的坐标为(0,27)或(0,﹣3);
(3)在第一象限内存在点P,使△PAB为等腰直角三角形;理由如下:
①当∠BAP=90°,AB=AP,则△PAB为等腰直角三角形,
如图1,过点P作PG⊥x轴于点G,
∴∠PGA=∠AOB=90°,
∵∠BAP=90°,
∴∠BAO+∠PAG=90°,
∵∠ABO+∠BAO=90°,
∴∠ABO=∠PAG,
在△AOB和△PGA中,∠ABO=∠PAG,∠AOB=∠PGA,AB=PA,
∴△AOB≌△PGA(AAS),
∴OA=PG=9,OB=AG=12,
∴OG=OA+AG=21,
∴点P的坐标为(21,9);
②当∠ABP=90°,BA=BP,则△PAB为等腰直角三角形,
如图2,过点P作PH⊥y轴于点H,
同理 可证,△AOB≌△BHP(AAS),
∴OA=BH=9,PH=OB=12,
∴OH=OB+BH=21,
∴点P的坐标为(12,21);
③当∠APB=90°,PA=PB,则△PAB为等腰直角三角形,
如图3,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PNB=∠PMA=∠MPN=90°,
∴∠APN+∠APM=90°,
∵∠APB=90°,
∴∠BPN+∠APN=90°,
∴∠APM=∠BPN,
在△APM和△BPN中,∠APM=∠BPN,PA=PB,∠PMA=∠PNB,
∴△APM≌△BPN(ASA),
∴AM=BN,PM=PN,
∴设点P的坐标为(p,p),
∴OM=ON=p,
∴BN=OB﹣ON=12﹣p,AM=OM﹣OA=p﹣9,
∴12﹣p=p﹣9,
解得:p,则点P的坐标为(,),
综上可知,第一象限内存在点P,使△PAB为等腰直角三角形,点P的坐标(21,9)或(12,21)或(,).
9.【解答】解:(1)在y=x+3中,令x=0得y=3,令y=0得x=﹣3,
∴A(﹣3,0),C(0,3),
∵直线BC与直线AC关于y轴对称,
∴点B与点A关于y轴对称,
∴B(3,0);
(2)设直线BC的解析式为y=kx+b,把点C(0,3)和点B(3,0)的坐标代入得:
,解得:,
∴直线BC的解析式为y=﹣x+3;
当点P在直线CA上时,m+3=2,
解得m=﹣1,
当点P在直线BC上时,﹣m+3=2,
解得m=1,
∴当点P在△ABC的内部时,m的取值范围是﹣1<m<1;
(3)∵A(﹣3,0),C(0,3),B(3,0),
∴S△ABC=×6×3=9;
①设直线L交AC于K,S△AOK:S四边形KOBC=1:2,过K作KH⊥AB于H,如图:
∴S△AOKS△ABC=3,
∴3×HK=3,
则KH=2,
在y=x+3中,令y=2,
即2=x+3,
解得:x=﹣1,
∴K(﹣1,2)
设直线L解析式为y=px,
∴2=﹣p,
解得p=﹣2,
∴直线L解析式为y=﹣2x;
②设直线L交BC于T,S△BOT:S四边形AOTC=1:2,过T作TH'⊥AB于H',如图:
同理可得:3×TH′=3,
解得:TH′=2,
在y=﹣x+3中,令y=2得x=1,
则点T(1,2),
则直线L解析式为y=2x;
综上所述,直线L的解析式为y=﹣2x或y=2x.
10.【解答】解:(1)对于yx,令x=0,则y,令y=0,解得x=﹣2,
故点A、B的坐标分别为(﹣2,0)、(0,);
(2)①设直线AP交y轴于点H,
设直线AP的表达式为:y=k(x+2),
当x=0时,y=2k,当x=2时,y=4k,
即点H、P的坐标分别为(0,2k),(2,4k),
则△ABP的面积=S△HBP+S△HBAAC BH4(2k),
解得:k,
∴点P的坐标为(2,);
当点P在点D的上方时,根据对称性可知P(2,),
综上所述,点P的坐标为(2,)或(2,),
②由(1)(2)知,P(2,),A(﹣2,0),B(0,),设点Q(s,t),
∵点A、B、P、Q为顶点的四边形是平行四边形,
∴①Ⅰ、以AP为对角线,由中点坐标公式得,
∴,
∴点Q(0,﹣3),
Ⅱ、以AB为对角线,由中点坐标公式得,
∴,
∴点Q(﹣4,3);
Ⅲ、以AQ为对角线,由中点坐标公式得,
∴,
∴Q(4,0),
综上所述,以点A、B、P、Q为顶点的四边形是平行四边形,点Q坐标为(0,﹣3)或(﹣4,3)或(4,0).
11.【解答】【模型建立】证明:∵AD⊥ED,BE⊥ED,
∴∠BEC=∠ADC=90°,
∴∠ACD+∠DAC=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠BCE=∠CAD,
在△BEC和△CDA中,
,
∴△BEC≌△CDA(AAS);
(1)解:①∵OC=1,
∴点C的坐标是(1,0),
由【模型建立】得△BOC≌△CDA,
∴AD=OC=1,CD=OB=2,
∴OD=OC+CD=3,
∴点A的坐标是(3,1);
故答案为:(1,0),(3,1);
②如图2,当M在x轴正半轴时,连接OA,
∵点A的坐标是(3,1),OB=2,
S△AOB2×3=3,
∴S△OAM=S四边形﹣S△AOB=4﹣3=1,
∴OM×1=1,
OM=2,
∴M(2,0),
如图2.2,当M在x轴负半轴时,连接OA,
∵点A的坐标是(3,1),OB=2,
S△AOB2×3=3,
∴S△OBM=S四边形﹣S△AOB=4﹣3=1,
∴OM OB=1,
∴OM=1,
∴M(﹣1,0),
故答案为:(2,0)或(﹣1,0);
(2)解:过点B作BF⊥l2于点F,
∵将直线l1绕点A逆时针旋转45°至直线l2,
∴△ABF是等腰直角三角形,
∵直线l1:y=2x+4与x轴交于点A,与y轴交于点B,
∴A(﹣2,0),B(0,4),
∴OA=2,OB=4,
∴AB2,
∴AF=BFAB,
设l2的函数解析式为y=kx+4,则F(a,ka+4),依题意得:
,
解得:或,
∴直线l2的函数解析式为yx+4或y=﹣3x+4.
12.【解答】解:(1)将点B的坐标(0,6)代入解析式y=kx+8k,
得8k=6,
解得,
∴,
当y=0时,,
解得x=﹣8,
∴点A的坐标为(﹣8,0);
(2)过点D作DE⊥x轴于点E,∠DEA=90°,
由旋转可知,AB=AD,∠BAD=90°,
∴∠BAO+∠DAO=90°,
又∵∠BAO+∠ABO=90°,
∴∠DAE=∠ABO,
在△AOB和△DEA中,
,
∴△AOB≌△DEA(AAS),
∴AE=OB=6,DE=OA=8,
∴OE=AO﹣AE=2,
∴D(﹣2,﹣8),
设直线BC的解析式为y=ax+b,
,
解得,
∴直线BC的解析式为y=7x+6;
(3)在Rt△AOB中,,
∵△AOB≌△DEA(AAS),
∴AD=AB=10,
∴,
对于y=7x+6,
当y=0时,7x+6=0,
∴,
则点C的坐标是,
设点P的坐标为(m,0),则,
则,
∵△BDP的面积是△ABD面积的一半,
∴,
∴,或,
∴点P的坐标为或.
13.【解答】解:(1)依题意可知,折痕CE是四边形OCAB的对称轴,
在Rt△CBD中,OC=CD=10,BC=OA=8,
由勾股定理,得BD6,
∴AD=BA﹣BD=10﹣6=4,
∴D(4,8).
在Rt△DAE中,由勾股定理,得AE2+AD2=DE2,
又DE=OE,AE=8﹣OE,
(8﹣OE)2+42=OE2,
解得OE=5,
∴E(0,5).
∴E(0,5),D(4,8);
故答案为:4,8;0,5;
(2)设D、E两点所在的直线的解析式为y=kx+b,
则,解得,
所以过D、E两点的直线函数表达式为yx+5.
(3)∵直线y=kx+b与DE平行,
∴k,
∵直线过长方形OABC的顶点C(10,0),
∴,
∴b,
∴直线CF的解析式为y,
∴x=0时,y,
∴F(0,),
∴OF,
∴△OCF的面积.
14.【解答】解:(1)对于,当x=0时,y=4,当y=0时,x=3,
即点A、B的坐标分别为:(3,0)、(0,4),
设直线BC的表达式为:y=kx+4,
将点C的坐标代入上式得:0=﹣2k+4,则k=2,
则直线BC的表达式为:y=2x+4;
(2)当∠DAC=90°时,则点A、D的横坐标相同,
当x=3时,y=2x+4=10,
即点D(3,10).
15.【解答】解:(1)把A(0,2),B(﹣4,0)代入y=kx+b得:
,
解得,
∴直线AB解析式为yx+2,
令y=3得3x+2,
解得x=2,
∴C的坐标为(2,3);
(2)如图:
∵P(0,4),A(0,2),
∴PA=2,
∵C(2,3),B(﹣4,0),
∴S△APC2×2=2,S△APB2×4=4,
∴S△PBC=2+4=6,
∴△PBC的面积为6;
(3)过B作BH⊥CP交CP延长线于H,过H作MN∥x轴,过B过BN⊥MN于N,过C作CM⊥MN于M,
设H(m,n),
当P在BC上方时,如图:
∵∠BCP=45°,BH⊥CP,
∴△BCH是等腰直角三角形,∠BHC=90°,
∴BH=CH,∠BHN=90°﹣∠MHC=∠MCH,
∵∠N=∠M=90°,
∴△BHN≌△HCM(AAS),
∴BN=HM,NH=CM,
∵B(﹣4,0),C(2,3),
∴,
解得,
∴H(﹣2.5,4.5),
由H(﹣2.5,4.5),C(2,3)得直线CH解析式为yx,
令x=0得y;
∴P(0,);
当P在BC下方时,如图:
同理可得BN=MH,NH=CM,
∴,
解得,
∴H(,),
由H(,),C(2,3)可得CP解析式为y=3x﹣3,
令x=0得y=﹣3,
∴P(0,﹣3);
综上所述,P的坐标为P(0,)或(0,﹣3).
21世纪教育网(www.21cnjy.com)
同课章节目录
