2025年九年级中考数学三轮冲刺训练一次函数的应用练习(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练一次函数的应用练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 510.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 16:51:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练一次函数的应用练习
一、选择题
1.某公司打算与出租车公司签订租车合同.每月行驶x千米时,甲出租车公司的月租费用是y1元,乙出租车公司的月租车费用是y2元,y1、y2与x之间的函数关系如图所示,那么下列说法错误的是( )
A.x=1500千米时,两家公司的租车费用相同
B.x=750千米时,甲公司的租车费用为150元
C.x>1500千米时,甲公司的费用比乙公司低
D.x=3000千米时,两公司的租车费用相差150元.
2.某种气体在10℃时的体积为100L,温度每升高1C,它的体积增加0.35L,则该气体的体积V(L)与温度t(℃之间的函数表达式是( )
A.V=100+0.35(t﹣10) B.V=100+0.35(t+10)
C.V=100﹣0.35(t﹣10) D.V=100﹣0.35(t+10)
3.某品牌鞋子的长度y cm与鞋子的“码”数x之间满足一次函数关系,若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则42码鞋子的长度为( )
A.23cm B.24cm C.25cm D.26cm
4.某物理兴趣小组调查了解到:声音在干燥空气中传播的速度v(m/s)是空气温度t(℃)的一次函数,部分数据如下表所示,则v与t之间的关系式为( )
温度t/℃ 10 20 40
声速v(m/s) 337 343 355
A.v=0.6t+331 B.y=0.6t﹣331
C.v=6t+337 D.v=6t
5.如图,货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离分别为y1(单位:km)、y2(单位:km),图中的线段OA、折线BCDE分别表示y1,y2与x之间的函数关系.有下列四个结论:①轿车行驶的速度为125km/h;②货车行驶的速度为65km/h;③线段DE所在直线的函数表达式为y=﹣125x+800;④两车出发2小时或4小时后相距150km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.③④
二、填空题
6.已知A、B两地是一条直路,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,两人同时出发,乙先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,则下列结论正确的有 .
①两人出发2h后相遇;
②甲骑自行车的速度为60km/h;
③乙比甲提前2h到达目的地;
④乙到达目的地时两人相距200km.
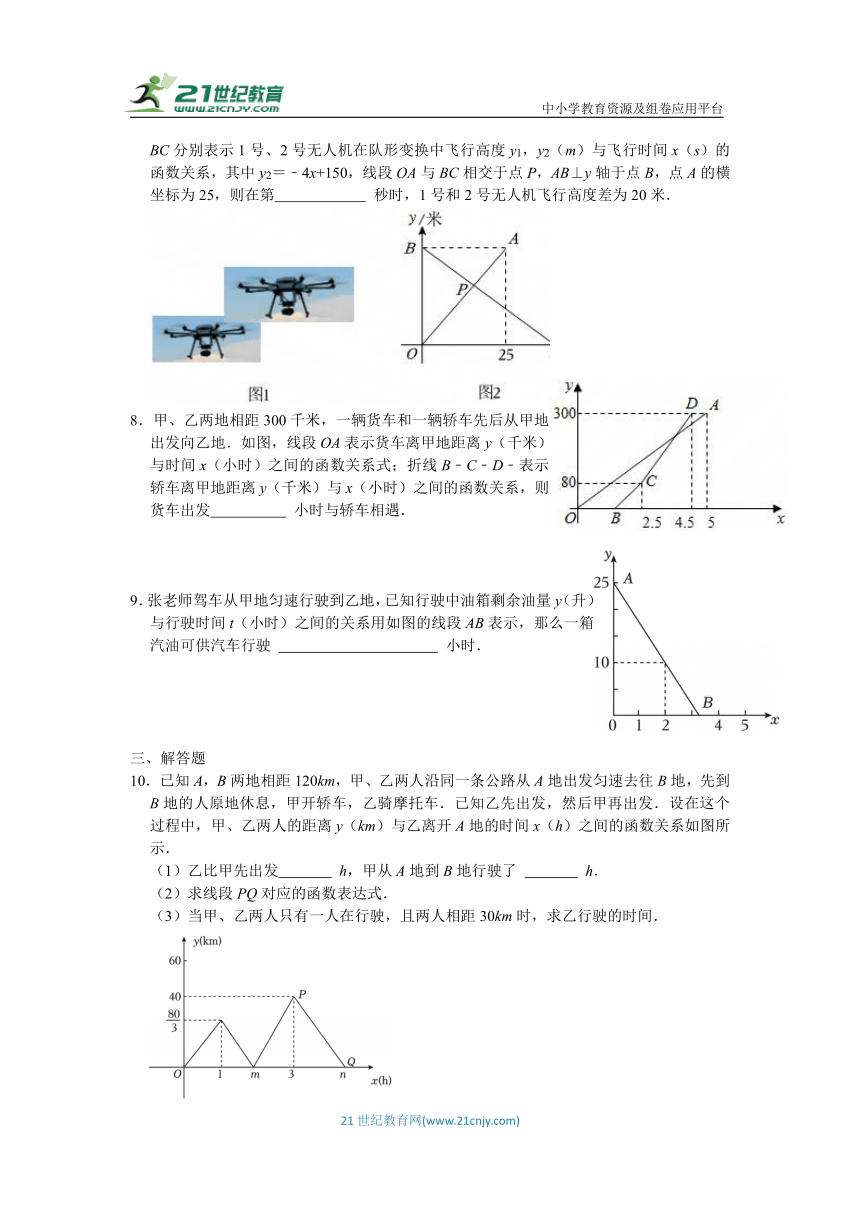
7.如图1,是在空中参与飞行表演的两架无人机,如图2,在平面直角坐标系中,线段OA,BC分别表示1号、2号无人机在队形变换中飞行高度y1,y2(m)与飞行时间x(s)的函数关系,其中y2=﹣4x+150,线段OA与BC相交于点P,AB⊥y轴于点B,点A的横坐标为25,则在第 秒时,1号和2号无人机飞行高度差为20米.
8.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D﹣表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,则货车出发 小时与轿车相遇.
9.张老师驾车从甲地匀速行驶到乙地,已知行驶中油箱剩余油量y(升)与行驶时间t(小时)之间的关系用如图的线段AB表示,那么一箱汽油可供汽车行驶 小时.
三、解答题
10.已知A,B两地相距120km,甲、乙两人沿同一条公路从A地出发匀速去往B地,先到B地的人原地休息,甲开轿车,乙骑摩托车.已知乙先出发,然后甲再出发.设在这个过程中,甲、乙两人的距离y(km)与乙离开A地的时间x(h)之间的函数关系如图所示.
(1)乙比甲先出发 h,甲从A地到B地行驶了 h.
(2)求线段PQ对应的函数表达式.
(3)当甲、乙两人只有一人在行驶,且两人相距30km时,求乙行驶的时间.
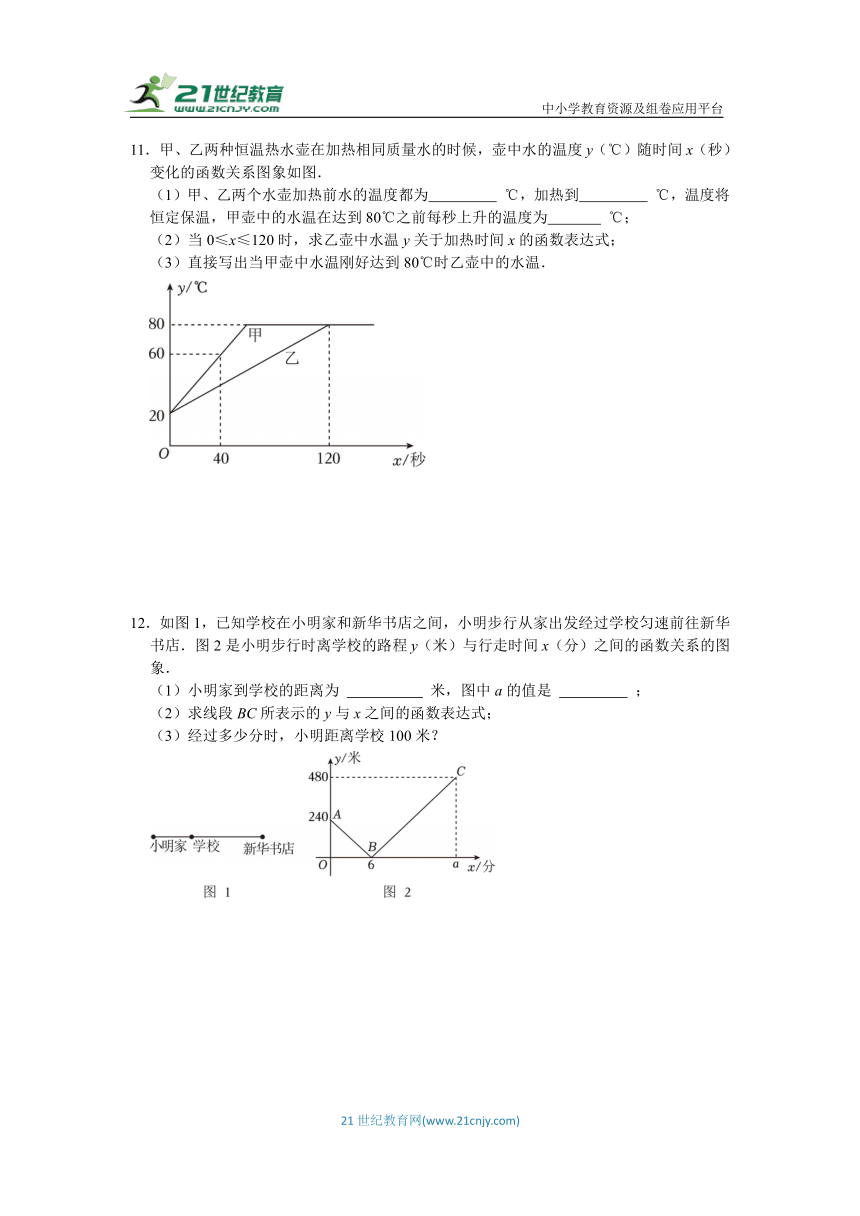
11.甲、乙两种恒温热水壶在加热相同质量水的时候,壶中水的温度y(℃)随时间x(秒)变化的函数关系图象如图.
(1)甲、乙两个水壶加热前水的温度都为 ℃,加热到 ℃,温度将恒定保温,甲壶中的水温在达到80℃之前每秒上升的温度为 ℃;
(2)当0≤x≤120时,求乙壶中水温y关于加热时间x的函数表达式;
(3)直接写出当甲壶中水温刚好达到80℃时乙壶中的水温.
12.如图1,已知学校在小明家和新华书店之间,小明步行从家出发经过学校匀速前往新华书店.图2是小明步行时离学校的路程y(米)与行走时间x(分)之间的函数关系的图象.
(1)小明家到学校的距离为 米,图中a的值是 ;
(2)求线段BC所表示的y与x之间的函数表达式;
(3)经过多少分时,小明距离学校100米?
13.某超市销售A,B两种品牌的牛奶,购买3箱A种品牌的牛奶和2箱B种品牌的牛奶共需285元;购买2箱A种品牌的牛奶和5箱B种品牌的牛奶共需410元.
(1)求A种品牌的牛奶,B种品牌的牛奶每箱价格分别是多少元?
(2)若某公司购买A,B两种品牌的牛奶共20箱,且A种品牌牛奶的数量至少比B种品牌牛奶的数量多6箱,又不超过B种品牌牛奶的3倍,购买A,B两种品牌的牛奶各多少箱才能使总费用最少?最少总费用为多少元?
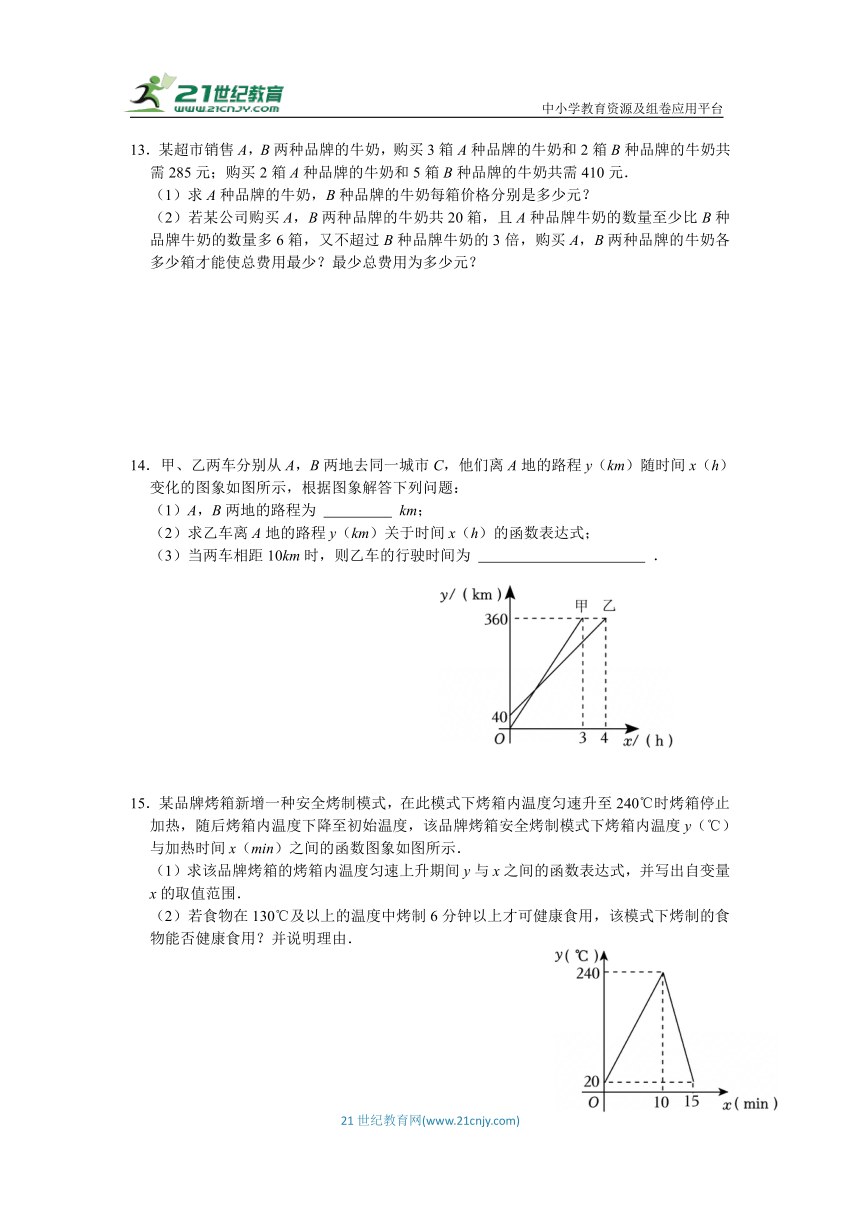
14.甲、乙两车分别从A,B两地去同一城市C,他们离A地的路程y(km)随时间x(h)变化的图象如图所示,根据图象解答下列问题:
(1)A,B两地的路程为 km;
(2)求乙车离A地的路程y(km)关于时间x(h)的函数表达式;
(3)当两车相距10km时,则乙车的行驶时间为 .
15.某品牌烤箱新增一种安全烤制模式,在此模式下烤箱内温度匀速升至240℃时烤箱停止加热,随后烤箱内温度下降至初始温度,该品牌烤箱安全烤制模式下烤箱内温度y(℃)与加热时间x(min)之间的函数图象如图所示.
(1)求该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数表达式,并写出自变量x的取值范围.
(2)若食物在130℃及以上的温度中烤制6分钟以上才可健康食用,该模式下烤制的食物能否健康食用?并说明理由.
参考答案
一、选择题
1.【解答】解:由题意知:当0<x<1500时,y1的图象在y2的图象上方;当x>1500时,y2的图象在y1的图象上方,
A、每月行驶1500千米时,两家公司的租车费用相同,
故该选项说法正确,不符合题意;
B、设y1关于x的函数关系式为y1=kx+b,
由题意得:,
解得:,
∴,
∴每月行驶750千米时,甲公司的租车费用为(元),
∴每月行驶750千米时,甲公司的租车费用为150元,
故该选项说法正确,不符合题意;
C、每月行驶超过1500千米时,租用甲公司的费用比乙公司低,
故该选项说法正确,不符合题意;
D、设y2关于x的函数关系式为y2=k'x,
由题意得:1500k′=200,
解得:,
∴,
∴每月行驶3000千米时,
,
,
400﹣300=100(元),
∴租用乙公司的租车费用比甲公司多100元,
故该选项说法错误,符合题意;
故选:D.
2.【解答】解:V与t之间的函数表达式为V=100+0.35(t﹣10).
故选:A.
3.【解答】解:由某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系,设y=kx+b,
∵22码鞋子的长度为16cm,44码鞋子的长度为27cm,
∴,
解得,
∴yx+5,
当x=42时,y42+5=26,
故选:D.
4.【解答】解:设v与t之间的关系式为v=kt+b(k、b为常数,且k≠0).
将t=10,v=337和t=20,v=343分别代入v=kt+b,
得,
解得,
∴v与t之间的关系式为v=0.6t+331.
故选:A.
5.【解答】解:由图象可得,轿车的速度为:300÷2.4=125km/h,故①正确;
由图象可得,货车行驶的速度为:600÷8=75km/h,故②错误;
由题意可得OA所在直线为关于x的正比例函数,
设直线OA的解析式为:y=px,
由条件可得:600=8p,
解得p=75,
∴直线OA的解析式为y=75x;
在y=75x中,当y=300时,x=4,
∴点D的坐标为(4,300),
由条件可知轿车行驶后300km需2.4h.
∴点E坐标为:(6.4,0).
设线段DE所在直线的函数表达式为y=kx+b,
将点D(4,300),E(6.4,0)代入得:,
解得,
∴线段DE所在直线的函数表达式为y=﹣125x+800,故③正确;
在y=75x中,当x=2.4,y=180,
∴相遇前二者在前2.4h内存在某个时间段相距150km,
设BC段的函数解析式为y=mx+n,
将B(0,600),C(2.4,300)代入得:,
解得,
∴BC段的函数解析式为y=﹣125x+600,
当轿车休息前相距150km时,有﹣125x+600﹣75x=150,
解得x=2.25;
当轿车休息后相距150km时,有75x﹣(﹣125x+800)=150,
解得x=4.75.
即两车出发2.25小时或4.75小时后相距150km.故④错误.
故选:A.
二、填空题
6.【解答】解:∵横轴表示运动时间,纵轴表示两人之间的距离.∴图上的第一个点(0.300),表示甲乙两人还未出发时,相距300km,也就是A、B两地相距300km.第二个点(2,0),表示甲乙两人出发2小时时,两人相距0米,即相遇,故①正确;
最后一个点(5,300)表示走得慢的甲5小时走完300千米,也到了自己的目的地,此时两人相距300千米,所以甲骑自行车的速度为300÷5=60km/h,故②正确;
∵甲、乙两小时走完300km,∴甲、乙的速度和=300÷2=150km/h,∴乙的速度=150﹣60=90km/h.∴乙走完全程的时间=300÷90h.∴乙比甲提前到达的时间为5h,故③不正确;
乙到达目的地A时,走了时,此时甲离开A的路程为:60200km,此时两人相距200km,故④正确.
故答案为:①②④.
7.【解答】解:当x=0时,y2=150,
∴点B的坐标为(0,150),
由题意知点A的坐标为(25,150),
设y1=kx(k≠0),
将(25,150)代入y1=kx得150=25x,
∴x=6,
∴y1=6x,
∴线段OA对应的函数表达式为:y1=6x,
当1号和2号无人机飞行高度差为20米时,得:
|﹣4x+150﹣6x|=20,
解得:x=13或17,
∴在第13或17秒时,1号和2号无人机飞行高度差为20米.
故答案为:13或17.
8.【解答】解:设OA段对应的函数解析式为y=kx,
将(5,300)代入,得:5k=300,
解得k=60,
即OA段对应的函数解析式为y=60x,
设CD段对应的函数解析式为y=ax+b,
,
解得,
即CD段对应的函数解析式为y=110x﹣195,
令110x﹣195=60x,得x=3.9,
即货车出发3.9小时与轿车相遇,
故答案为:3.9.
9.【解答】解:y与t的函数关系式为y=kx+b(k、b为常数,且k≠0).
将坐标(0,25)和(2,10)分别代入y=kx+b,
得,
解得,
∴y与t的函数关系式为yx+25,
当y=0时,得x+25=0,
解得x,
∴一箱汽油可供汽车行驶小时.
故答案为:.
三、解答题
10.【解答】解:(1)由图象可知,乙比甲先出发1小时;甲到达B地用了:3﹣1=2(小时),
故答案为:1;2;
(2)根据题意,,
∴Q(4.5,0),
设线段PQ对应的函数表达式为y=kx+b,将P,Q的坐标分别代入得:
,
解得,
∴线段PQ对应的函数表达式为;
(3)①甲没有出发时,得:,
解得,
不合题意;
②甲到达B地时,得:,
解得.
综上所述,当甲、乙两人只有一人在行驶,且两人相距30km时,乙行驶的时间为小时.
11.【解答】解:(1)由函数图象可知,当x=0时,y=20,
则加热前水温是20℃,
加热到80℃,温度将恒定保温,
甲壶中的水温在达到80℃之前每秒上升的温度为℃,
(2)设乙壶为y=kx+b,
把(0,20),(120,80)代入可得:
,
解得:,
∴;
(3)∵甲壶中的水温在达到80℃之前每秒上升的温度为1℃,
∴当甲壶中水温刚好达到80℃时,t=(80﹣20)×1=60,
∴,
∴当甲壶中水温刚好达到80℃时,乙壶中的水温为50℃.
12.【解答】解:(1)小明家到学校的距离为240米;
小明步行的速度是240÷6=40(米/分),
小明家到新华书店的距离为240+480=720(米),
则小明从家到新华书店所用时间为720÷40=18(分),
∴a=18.
故答案为:240,18.
(2)设线段BC所表示的y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将坐标B(6,0)和C(18,480)分别代入y=kx+b,
得,
解得,
∴线段BC所表示的y与x之间的函数表达式为y=40x﹣240(6≤x≤18).
(3)当0≤x<6时,240﹣40x=100,
解得x=3.5;
当6≤x≤18时,40x﹣240=100,
解得x=8.5.
答:经过3.5分或8.5分时,小明距离学校100米.
13.【解答】解:(1)设A种品牌的牛奶每箱价格是a元,B种品牌的牛奶每箱价格是b元.
根据题意,得,
解得.
答:A种品牌的牛奶每箱价格是55元,B种品牌的牛奶每箱价格是60元.
(2)设购买A品牌的牛奶x箱,则购买B品牌的牛奶(20﹣x)箱.
根据题意,得,
解得13≤x≤15,
设总费用为W元,则W=55x+60(20﹣x)=﹣5x+1200,
∵﹣5<0,
∴W随x的增大而减小,
∵13≤x≤15,
∴当x=15时,W值最小,W最小=﹣5×15+1200=1125,20﹣15=5(箱).
答:购买A品牌的牛奶15箱、B品牌的牛奶5箱才能使总费用最少,最少总费用为1125元.
14.【解答】解:(1)根据图象,A,B两地的路程为40km.
故答案为:40.
(2)乙车的速度为(360﹣40)÷4=80(km/h),
则y=40+80x=80x+40,
∴乙车离A地的路程y关于时间x的函数表达式为y=80x+40(0≤x≤4).
(3)甲车的速度为360÷3=120(km/h),
则甲车离A地的路程y关于时间x的函数表达式为y=120x(0≤x≤3),
当0≤x≤3时,当两车相距10km时,得|120﹣(80x+40)|=10,
解得x或;
当3<x≤4时,当两车相距10km时,得360﹣(80x+40)=10,
解得x.
答:当两车相距10km时,则乙车的行驶时间为h或h或h.
15.【解答】解:(1)设该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数关系为y=kx+b,将(0,20),(10,240)分别代入得:
,
解得,
∴该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数关系式为y=22x+20(0≤x≤10);
(2)设该品牌烤箱的烤箱内温度匀速下降期间y与x之间的函数关系为y=mx+n.将(15,0),(10,240)分别代入得:
,
解得,
∴该品牌烤箱的烤箱内温度匀速下降期间y与x之间的函数关系式为y=﹣44x+680(10≤x≤15).
当0≤x≤10时,
令y=130,得:22 x+20=130,
解得x=5;
当10≤x≤15时,
令y=130,得:130=﹣44x+680,
解得x=12.5,
∵12.5﹣5=7.5>6,
∴该模式下烤制的食物能健康食用.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练一次函数的应用练习
一、选择题
1.某公司打算与出租车公司签订租车合同.每月行驶x千米时,甲出租车公司的月租费用是y1元,乙出租车公司的月租车费用是y2元,y1、y2与x之间的函数关系如图所示,那么下列说法错误的是( )
A.x=1500千米时,两家公司的租车费用相同
B.x=750千米时,甲公司的租车费用为150元
C.x>1500千米时,甲公司的费用比乙公司低
D.x=3000千米时,两公司的租车费用相差150元.
2.某种气体在10℃时的体积为100L,温度每升高1C,它的体积增加0.35L,则该气体的体积V(L)与温度t(℃之间的函数表达式是( )
A.V=100+0.35(t﹣10) B.V=100+0.35(t+10)
C.V=100﹣0.35(t﹣10) D.V=100﹣0.35(t+10)
3.某品牌鞋子的长度y cm与鞋子的“码”数x之间满足一次函数关系,若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则42码鞋子的长度为( )
A.23cm B.24cm C.25cm D.26cm
4.某物理兴趣小组调查了解到:声音在干燥空气中传播的速度v(m/s)是空气温度t(℃)的一次函数,部分数据如下表所示,则v与t之间的关系式为( )
温度t/℃ 10 20 40
声速v(m/s) 337 343 355
A.v=0.6t+331 B.y=0.6t﹣331
C.v=6t+337 D.v=6t
5.如图,货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离分别为y1(单位:km)、y2(单位:km),图中的线段OA、折线BCDE分别表示y1,y2与x之间的函数关系.有下列四个结论:①轿车行驶的速度为125km/h;②货车行驶的速度为65km/h;③线段DE所在直线的函数表达式为y=﹣125x+800;④两车出发2小时或4小时后相距150km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.③④
二、填空题
6.已知A、B两地是一条直路,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,两人同时出发,乙先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,则下列结论正确的有 .
①两人出发2h后相遇;
②甲骑自行车的速度为60km/h;
③乙比甲提前2h到达目的地;
④乙到达目的地时两人相距200km.
7.如图1,是在空中参与飞行表演的两架无人机,如图2,在平面直角坐标系中,线段OA,BC分别表示1号、2号无人机在队形变换中飞行高度y1,y2(m)与飞行时间x(s)的函数关系,其中y2=﹣4x+150,线段OA与BC相交于点P,AB⊥y轴于点B,点A的横坐标为25,则在第 秒时,1号和2号无人机飞行高度差为20米.
8.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系式;折线B﹣C﹣D﹣表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,则货车出发 小时与轿车相遇.
9.张老师驾车从甲地匀速行驶到乙地,已知行驶中油箱剩余油量y(升)与行驶时间t(小时)之间的关系用如图的线段AB表示,那么一箱汽油可供汽车行驶 小时.
三、解答题
10.已知A,B两地相距120km,甲、乙两人沿同一条公路从A地出发匀速去往B地,先到B地的人原地休息,甲开轿车,乙骑摩托车.已知乙先出发,然后甲再出发.设在这个过程中,甲、乙两人的距离y(km)与乙离开A地的时间x(h)之间的函数关系如图所示.
(1)乙比甲先出发 h,甲从A地到B地行驶了 h.
(2)求线段PQ对应的函数表达式.
(3)当甲、乙两人只有一人在行驶,且两人相距30km时,求乙行驶的时间.
11.甲、乙两种恒温热水壶在加热相同质量水的时候,壶中水的温度y(℃)随时间x(秒)变化的函数关系图象如图.
(1)甲、乙两个水壶加热前水的温度都为 ℃,加热到 ℃,温度将恒定保温,甲壶中的水温在达到80℃之前每秒上升的温度为 ℃;
(2)当0≤x≤120时,求乙壶中水温y关于加热时间x的函数表达式;
(3)直接写出当甲壶中水温刚好达到80℃时乙壶中的水温.
12.如图1,已知学校在小明家和新华书店之间,小明步行从家出发经过学校匀速前往新华书店.图2是小明步行时离学校的路程y(米)与行走时间x(分)之间的函数关系的图象.
(1)小明家到学校的距离为 米,图中a的值是 ;
(2)求线段BC所表示的y与x之间的函数表达式;
(3)经过多少分时,小明距离学校100米?
13.某超市销售A,B两种品牌的牛奶,购买3箱A种品牌的牛奶和2箱B种品牌的牛奶共需285元;购买2箱A种品牌的牛奶和5箱B种品牌的牛奶共需410元.
(1)求A种品牌的牛奶,B种品牌的牛奶每箱价格分别是多少元?
(2)若某公司购买A,B两种品牌的牛奶共20箱,且A种品牌牛奶的数量至少比B种品牌牛奶的数量多6箱,又不超过B种品牌牛奶的3倍,购买A,B两种品牌的牛奶各多少箱才能使总费用最少?最少总费用为多少元?
14.甲、乙两车分别从A,B两地去同一城市C,他们离A地的路程y(km)随时间x(h)变化的图象如图所示,根据图象解答下列问题:
(1)A,B两地的路程为 km;
(2)求乙车离A地的路程y(km)关于时间x(h)的函数表达式;
(3)当两车相距10km时,则乙车的行驶时间为 .
15.某品牌烤箱新增一种安全烤制模式,在此模式下烤箱内温度匀速升至240℃时烤箱停止加热,随后烤箱内温度下降至初始温度,该品牌烤箱安全烤制模式下烤箱内温度y(℃)与加热时间x(min)之间的函数图象如图所示.
(1)求该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数表达式,并写出自变量x的取值范围.
(2)若食物在130℃及以上的温度中烤制6分钟以上才可健康食用,该模式下烤制的食物能否健康食用?并说明理由.
参考答案
一、选择题
1.【解答】解:由题意知:当0<x<1500时,y1的图象在y2的图象上方;当x>1500时,y2的图象在y1的图象上方,
A、每月行驶1500千米时,两家公司的租车费用相同,
故该选项说法正确,不符合题意;
B、设y1关于x的函数关系式为y1=kx+b,
由题意得:,
解得:,
∴,
∴每月行驶750千米时,甲公司的租车费用为(元),
∴每月行驶750千米时,甲公司的租车费用为150元,
故该选项说法正确,不符合题意;
C、每月行驶超过1500千米时,租用甲公司的费用比乙公司低,
故该选项说法正确,不符合题意;
D、设y2关于x的函数关系式为y2=k'x,
由题意得:1500k′=200,
解得:,
∴,
∴每月行驶3000千米时,
,
,
400﹣300=100(元),
∴租用乙公司的租车费用比甲公司多100元,
故该选项说法错误,符合题意;
故选:D.
2.【解答】解:V与t之间的函数表达式为V=100+0.35(t﹣10).
故选:A.
3.【解答】解:由某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系,设y=kx+b,
∵22码鞋子的长度为16cm,44码鞋子的长度为27cm,
∴,
解得,
∴yx+5,
当x=42时,y42+5=26,
故选:D.
4.【解答】解:设v与t之间的关系式为v=kt+b(k、b为常数,且k≠0).
将t=10,v=337和t=20,v=343分别代入v=kt+b,
得,
解得,
∴v与t之间的关系式为v=0.6t+331.
故选:A.
5.【解答】解:由图象可得,轿车的速度为:300÷2.4=125km/h,故①正确;
由图象可得,货车行驶的速度为:600÷8=75km/h,故②错误;
由题意可得OA所在直线为关于x的正比例函数,
设直线OA的解析式为:y=px,
由条件可得:600=8p,
解得p=75,
∴直线OA的解析式为y=75x;
在y=75x中,当y=300时,x=4,
∴点D的坐标为(4,300),
由条件可知轿车行驶后300km需2.4h.
∴点E坐标为:(6.4,0).
设线段DE所在直线的函数表达式为y=kx+b,
将点D(4,300),E(6.4,0)代入得:,
解得,
∴线段DE所在直线的函数表达式为y=﹣125x+800,故③正确;
在y=75x中,当x=2.4,y=180,
∴相遇前二者在前2.4h内存在某个时间段相距150km,
设BC段的函数解析式为y=mx+n,
将B(0,600),C(2.4,300)代入得:,
解得,
∴BC段的函数解析式为y=﹣125x+600,
当轿车休息前相距150km时,有﹣125x+600﹣75x=150,
解得x=2.25;
当轿车休息后相距150km时,有75x﹣(﹣125x+800)=150,
解得x=4.75.
即两车出发2.25小时或4.75小时后相距150km.故④错误.
故选:A.
二、填空题
6.【解答】解:∵横轴表示运动时间,纵轴表示两人之间的距离.∴图上的第一个点(0.300),表示甲乙两人还未出发时,相距300km,也就是A、B两地相距300km.第二个点(2,0),表示甲乙两人出发2小时时,两人相距0米,即相遇,故①正确;
最后一个点(5,300)表示走得慢的甲5小时走完300千米,也到了自己的目的地,此时两人相距300千米,所以甲骑自行车的速度为300÷5=60km/h,故②正确;
∵甲、乙两小时走完300km,∴甲、乙的速度和=300÷2=150km/h,∴乙的速度=150﹣60=90km/h.∴乙走完全程的时间=300÷90h.∴乙比甲提前到达的时间为5h,故③不正确;
乙到达目的地A时,走了时,此时甲离开A的路程为:60200km,此时两人相距200km,故④正确.
故答案为:①②④.
7.【解答】解:当x=0时,y2=150,
∴点B的坐标为(0,150),
由题意知点A的坐标为(25,150),
设y1=kx(k≠0),
将(25,150)代入y1=kx得150=25x,
∴x=6,
∴y1=6x,
∴线段OA对应的函数表达式为:y1=6x,
当1号和2号无人机飞行高度差为20米时,得:
|﹣4x+150﹣6x|=20,
解得:x=13或17,
∴在第13或17秒时,1号和2号无人机飞行高度差为20米.
故答案为:13或17.
8.【解答】解:设OA段对应的函数解析式为y=kx,
将(5,300)代入,得:5k=300,
解得k=60,
即OA段对应的函数解析式为y=60x,
设CD段对应的函数解析式为y=ax+b,
,
解得,
即CD段对应的函数解析式为y=110x﹣195,
令110x﹣195=60x,得x=3.9,
即货车出发3.9小时与轿车相遇,
故答案为:3.9.
9.【解答】解:y与t的函数关系式为y=kx+b(k、b为常数,且k≠0).
将坐标(0,25)和(2,10)分别代入y=kx+b,
得,
解得,
∴y与t的函数关系式为yx+25,
当y=0时,得x+25=0,
解得x,
∴一箱汽油可供汽车行驶小时.
故答案为:.
三、解答题
10.【解答】解:(1)由图象可知,乙比甲先出发1小时;甲到达B地用了:3﹣1=2(小时),
故答案为:1;2;
(2)根据题意,,
∴Q(4.5,0),
设线段PQ对应的函数表达式为y=kx+b,将P,Q的坐标分别代入得:
,
解得,
∴线段PQ对应的函数表达式为;
(3)①甲没有出发时,得:,
解得,
不合题意;
②甲到达B地时,得:,
解得.
综上所述,当甲、乙两人只有一人在行驶,且两人相距30km时,乙行驶的时间为小时.
11.【解答】解:(1)由函数图象可知,当x=0时,y=20,
则加热前水温是20℃,
加热到80℃,温度将恒定保温,
甲壶中的水温在达到80℃之前每秒上升的温度为℃,
(2)设乙壶为y=kx+b,
把(0,20),(120,80)代入可得:
,
解得:,
∴;
(3)∵甲壶中的水温在达到80℃之前每秒上升的温度为1℃,
∴当甲壶中水温刚好达到80℃时,t=(80﹣20)×1=60,
∴,
∴当甲壶中水温刚好达到80℃时,乙壶中的水温为50℃.
12.【解答】解:(1)小明家到学校的距离为240米;
小明步行的速度是240÷6=40(米/分),
小明家到新华书店的距离为240+480=720(米),
则小明从家到新华书店所用时间为720÷40=18(分),
∴a=18.
故答案为:240,18.
(2)设线段BC所表示的y与x之间的函数表达式为y=kx+b(k、b为常数,且k≠0).
将坐标B(6,0)和C(18,480)分别代入y=kx+b,
得,
解得,
∴线段BC所表示的y与x之间的函数表达式为y=40x﹣240(6≤x≤18).
(3)当0≤x<6时,240﹣40x=100,
解得x=3.5;
当6≤x≤18时,40x﹣240=100,
解得x=8.5.
答:经过3.5分或8.5分时,小明距离学校100米.
13.【解答】解:(1)设A种品牌的牛奶每箱价格是a元,B种品牌的牛奶每箱价格是b元.
根据题意,得,
解得.
答:A种品牌的牛奶每箱价格是55元,B种品牌的牛奶每箱价格是60元.
(2)设购买A品牌的牛奶x箱,则购买B品牌的牛奶(20﹣x)箱.
根据题意,得,
解得13≤x≤15,
设总费用为W元,则W=55x+60(20﹣x)=﹣5x+1200,
∵﹣5<0,
∴W随x的增大而减小,
∵13≤x≤15,
∴当x=15时,W值最小,W最小=﹣5×15+1200=1125,20﹣15=5(箱).
答:购买A品牌的牛奶15箱、B品牌的牛奶5箱才能使总费用最少,最少总费用为1125元.
14.【解答】解:(1)根据图象,A,B两地的路程为40km.
故答案为:40.
(2)乙车的速度为(360﹣40)÷4=80(km/h),
则y=40+80x=80x+40,
∴乙车离A地的路程y关于时间x的函数表达式为y=80x+40(0≤x≤4).
(3)甲车的速度为360÷3=120(km/h),
则甲车离A地的路程y关于时间x的函数表达式为y=120x(0≤x≤3),
当0≤x≤3时,当两车相距10km时,得|120﹣(80x+40)|=10,
解得x或;
当3<x≤4时,当两车相距10km时,得360﹣(80x+40)=10,
解得x.
答:当两车相距10km时,则乙车的行驶时间为h或h或h.
15.【解答】解:(1)设该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数关系为y=kx+b,将(0,20),(10,240)分别代入得:
,
解得,
∴该品牌烤箱的烤箱内温度匀速上升期间y与x之间的函数关系式为y=22x+20(0≤x≤10);
(2)设该品牌烤箱的烤箱内温度匀速下降期间y与x之间的函数关系为y=mx+n.将(15,0),(10,240)分别代入得:
,
解得,
∴该品牌烤箱的烤箱内温度匀速下降期间y与x之间的函数关系式为y=﹣44x+680(10≤x≤15).
当0≤x≤10时,
令y=130,得:22 x+20=130,
解得x=5;
当10≤x≤15时,
令y=130,得:130=﹣44x+680,
解得x=12.5,
∵12.5﹣5=7.5>6,
∴该模式下烤制的食物能健康食用.
21世纪教育网(www.21cnjy.com)
同课章节目录
