第十九章一次函数单元测试(一)(含答案)
文档属性
| 名称 | 第十九章一次函数单元测试(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 258.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 16:21:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十九章一次函数单元测试(一)人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
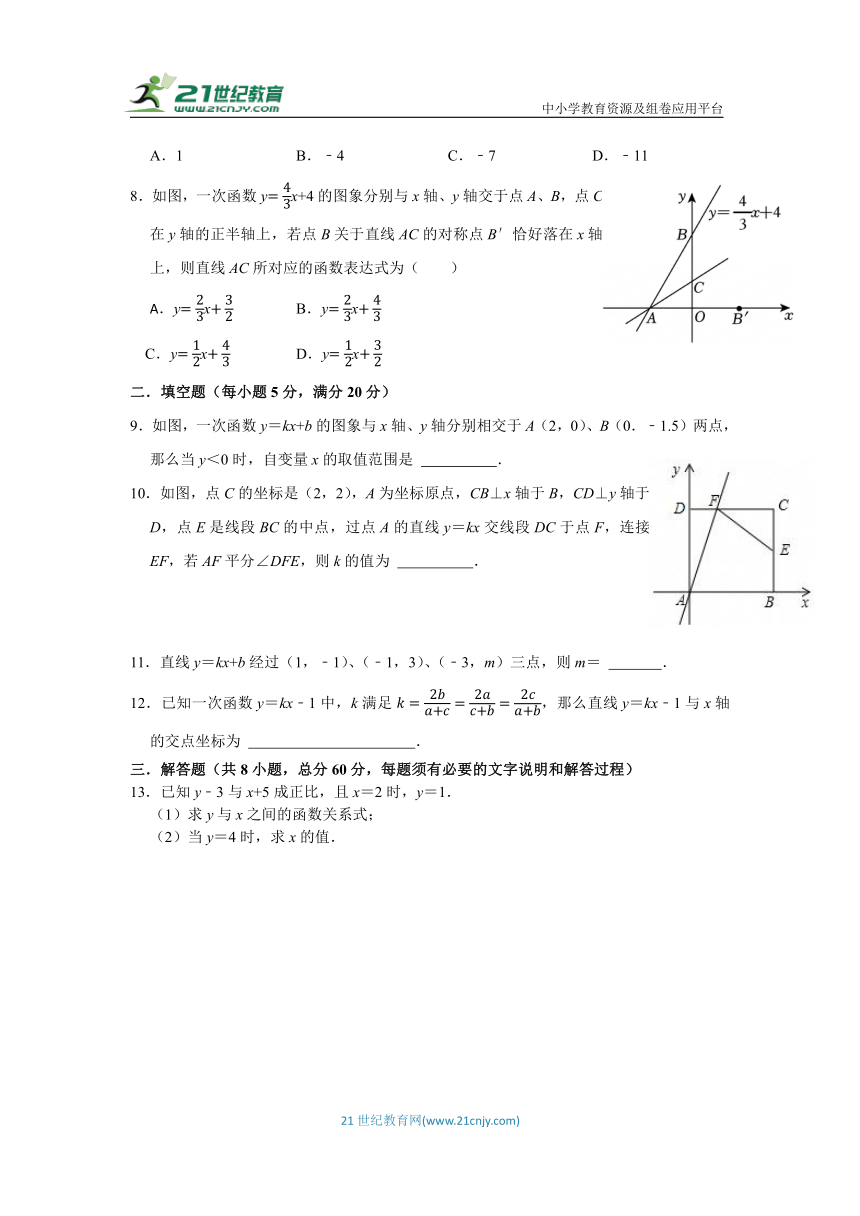
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.已知点(﹣2,y1)与点(5,y2)都在一次函数y=x+3的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1=y2 C.y1>y2 D.大小不能确定
2.一次函数y=2x﹣1的图象不会经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列图象中,表示y是x的函数的是( )
A.B. C.D.
4.若点A(2,﹣3),B(4,3),(5,a)在同一条直线上,则a的值是( )
A.6或﹣6 B.6 C.﹣6 D.6或3
5.在平面直角坐标系中,一次函数y=ax+a﹣1(a为常数,且a≠0)的图象一定经过的点是( )
A.(1,1) B.(﹣1,1) C.(﹣1,﹣1) D.(1,﹣1)
6.一次函数y=kx和y=﹣kx+k在同一平面直角坐标系中的图象可能是( )
A.B. C.D.
7.小磊在画一次函数的图象时列出了如下表格,小颖看到后说有一个函数值求错了.这个错误的函数值是( )
x … ﹣3 ﹣2 ﹣1 0 1 2 …
y … 9 5 1 ﹣4 ﹣7 ﹣11 …
A.1 B.﹣4 C.﹣7 D.﹣11
8.如图,一次函数yx+4的图象分别与x轴、y轴交于点A、B,点C在y轴的正半轴上,若点B关于直线AC的对称点B′恰好落在x轴上,则直线AC所对应的函数表达式为( )
yx B.yx
C.yx D.yx
二.填空题(每小题5分,满分20分)
9.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
10.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为 .
11.直线y=kx+b经过(1,﹣1)、(﹣1,3)、(﹣3,m)三点,则m= .
12.已知一次函数y=kx﹣1中,k满足,那么直线y=kx﹣1与x轴的交点坐标为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知y﹣3与x+5成正比,且x=2时,y=1.
(1)求y与x之间的函数关系式;
(2)当y=4时,求x的值.
14.已知一次函数y=(4+2m)x+m﹣4,求:
(1)m为何值时,y随x的增大而减少?
(2)m为何值时,函数图象与y轴的交点在x轴下方?
(3)若m=﹣1时,求此函数图象与x轴的交点坐标?
15.如图,已知一次函数yx+2的图象与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求△AOB的面积;
(2)若点P在一次函数yx+2的图象上,且在第一象限,S四边形OBPC,求点P的坐标.
16.如图,函数y=﹣2x+3与yx+m的图象交于P(n,﹣2).
(1)求出m、n的值;
(2)直接写出不等式x+m>﹣2x+3的解集;
(3)求出△ABP的面积.
17.如图,直线yx+b与x轴,y轴分别交于点A,点B,与函数y=kx的图象交于点M(1,2).
(1)直接写出k,b的值和不等式0的解集;
(2)在x轴上有一点P,过点P作x轴的垂线,分别交函数yx+b和y=kx的图象于点C,点D.若2CD=OB,求点P的坐标.
18.某家电销售商场电冰箱的销售价为每台1600元,空调的销售价为每台1400元,每台冰箱进价1500元,每台空调的进价1200元.现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售利润为y元,
(1)求出y与x之间的函数关系式;
(2)要求购进空调数量不超过电冰箱数量的2倍,总利润不低于16400元,请分析合理的方案共有多少种?
(3)实际进货时,厂家对电冰箱出厂价下调a(0<a<150)元,若商场保持这两种家电的售价不变,请你根据以上信息及(2)中条件,求出这100台家电销售时的最大利润.
参考答案
一、选择题
1—8:ABDBCBBD
二、填空题
9.答案为:x<2.
10.答案为:1或3.
11.答案为:7.
12.答案为:(,0)或(1,0).
三、解答题
13.【解答】解:(1)∵y﹣3与x+5成正比,
∴设y﹣3=k(x+5),
∵x=2时,y=1,
∴1﹣3=(2+5)k,
∴,
∴,
∴;
(2)当y=4时,
∴
即,
∴.
14.【解答】解:(1)∵y随x的增大而减小,
∴4+2m<0,
即m<﹣2,
当m<﹣2时,y随x的增大而减小.
(2)∵函数图象与y轴的交点在x轴下方,
∴m﹣4<0且4+2m≠0,
即m<4且m≠﹣2,
∴当m<4且m≠﹣2时,函数图象与y轴交点在x轴下方.
(3)若m=﹣1时,
则一次函数解析式为y=2x﹣5,
当函数图象与x轴相交,
∵交点纵坐标为0,
∴0=2x﹣5,即x,
∴此函数图象与x轴的交点坐标为(,0).
15.【解答】解:(1)在一次函数yx+2中,当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
∴S△AOB4;
(2)∵点C与点A关于y轴对称.
∴C(4,0),
如图,连接OP,
设点P(m,)(m>0),
S四边形OBPC=S△BOP+S△POC()=2m+4,
S△APC()=2m+8,
∵S四边形OBPC,
∴2m+4(2m+8),解得m=2.
∴P(2,3).
16.【解答】解:(1)∵y=﹣2x+3过P(n,﹣2).
∴﹣2=﹣2n+3,
解得:n,
∴P(,﹣2),
∵yx+m的图象过P(,﹣2).
∴﹣2m,
解得:m;
(2)不等式x+m>﹣2x+3的解集为x;
(3)∵当y=﹣2x+3中,x=0时,y=3,
∴A(0,3),
∵当yx中,x=0时,y,
∴B(0,),
∴AB=3;
∴△ABP的面积:AB.
17.【解答】解:(1)把M(1,2)代入y=kx得k=2;
把M(1,2)代入yx+b得2b,解得b;
当y=0时,x0,解得x=5,则A(5,0),
所以不等式0的解集为1≤x≤5;
(2)当x=0时,yx,则B(0,),
∴OB,
设P(m,0),则C(m,m),D(m,2m),
∵2CD=OB,
∴2|m2m|,
解得m或,
∴点P的坐标为P (,0)或 (,0).
18.【解答】解;(1)设购进电冰箱x台,这100台家电的销售利润为y元,
根据题意有:y=(1600﹣1500)x+(1400﹣1200)(100﹣x),
整理,得:y=20000﹣100x.
∴y与x之间的函数关系式为y=20000﹣100x;
(2)∵购进空调数量不超过电冰箱数量的2倍,
∴100﹣x≤2x,
解得:.
∵总利润不低于16400元,
∴y≥16400,即20000﹣100x≥16400,
解得:x≤36,
∴.
∵x为整数,
∴x的取值可以为34,35,36,
∴购买方案共有3种.
(3)根据题意有:y=[1600﹣(1500﹣a)]x+(1400﹣1200)(100﹣x),
整理,得:y=(a﹣100)x+20000.
当0<a<100时,a﹣100<0,
∴此时y随x的增大而减小,
∴当x=34时,y最大,ymax=(a﹣100)×34+20000=34a+16600;
当100<a<150时,a﹣100>0,
∴此时y随x的增大而增大,
∴当x=36时,y最大,ymax=(a﹣100)×36+20000=36a+16400;
当a=100时,y=20000.
∴最大利润为(36a+16400)元.
21世纪教育网(www.21cnjy.com)
第十九章一次函数单元测试(一)人教版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.已知点(﹣2,y1)与点(5,y2)都在一次函数y=x+3的图象上,则y1与y2的大小关系为( )
A.y1<y2 B.y1=y2 C.y1>y2 D.大小不能确定
2.一次函数y=2x﹣1的图象不会经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列图象中,表示y是x的函数的是( )
A.B. C.D.
4.若点A(2,﹣3),B(4,3),(5,a)在同一条直线上,则a的值是( )
A.6或﹣6 B.6 C.﹣6 D.6或3
5.在平面直角坐标系中,一次函数y=ax+a﹣1(a为常数,且a≠0)的图象一定经过的点是( )
A.(1,1) B.(﹣1,1) C.(﹣1,﹣1) D.(1,﹣1)
6.一次函数y=kx和y=﹣kx+k在同一平面直角坐标系中的图象可能是( )
A.B. C.D.
7.小磊在画一次函数的图象时列出了如下表格,小颖看到后说有一个函数值求错了.这个错误的函数值是( )
x … ﹣3 ﹣2 ﹣1 0 1 2 …
y … 9 5 1 ﹣4 ﹣7 ﹣11 …
A.1 B.﹣4 C.﹣7 D.﹣11
8.如图,一次函数yx+4的图象分别与x轴、y轴交于点A、B,点C在y轴的正半轴上,若点B关于直线AC的对称点B′恰好落在x轴上,则直线AC所对应的函数表达式为( )
yx B.yx
C.yx D.yx
二.填空题(每小题5分,满分20分)
9.如图,一次函数y=kx+b的图象与x轴、y轴分别相交于A(2,0)、B(0.﹣1.5)两点,那么当y<0时,自变量x的取值范围是 .
10.如图,点C的坐标是(2,2),A为坐标原点,CB⊥x轴于B,CD⊥y轴于D,点E是线段BC的中点,过点A的直线y=kx交线段DC于点F,连接EF,若AF平分∠DFE,则k的值为 .
11.直线y=kx+b经过(1,﹣1)、(﹣1,3)、(﹣3,m)三点,则m= .
12.已知一次函数y=kx﹣1中,k满足,那么直线y=kx﹣1与x轴的交点坐标为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.已知y﹣3与x+5成正比,且x=2时,y=1.
(1)求y与x之间的函数关系式;
(2)当y=4时,求x的值.
14.已知一次函数y=(4+2m)x+m﹣4,求:
(1)m为何值时,y随x的增大而减少?
(2)m为何值时,函数图象与y轴的交点在x轴下方?
(3)若m=﹣1时,求此函数图象与x轴的交点坐标?
15.如图,已知一次函数yx+2的图象与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求△AOB的面积;
(2)若点P在一次函数yx+2的图象上,且在第一象限,S四边形OBPC,求点P的坐标.
16.如图,函数y=﹣2x+3与yx+m的图象交于P(n,﹣2).
(1)求出m、n的值;
(2)直接写出不等式x+m>﹣2x+3的解集;
(3)求出△ABP的面积.
17.如图,直线yx+b与x轴,y轴分别交于点A,点B,与函数y=kx的图象交于点M(1,2).
(1)直接写出k,b的值和不等式0的解集;
(2)在x轴上有一点P,过点P作x轴的垂线,分别交函数yx+b和y=kx的图象于点C,点D.若2CD=OB,求点P的坐标.
18.某家电销售商场电冰箱的销售价为每台1600元,空调的销售价为每台1400元,每台冰箱进价1500元,每台空调的进价1200元.现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售利润为y元,
(1)求出y与x之间的函数关系式;
(2)要求购进空调数量不超过电冰箱数量的2倍,总利润不低于16400元,请分析合理的方案共有多少种?
(3)实际进货时,厂家对电冰箱出厂价下调a(0<a<150)元,若商场保持这两种家电的售价不变,请你根据以上信息及(2)中条件,求出这100台家电销售时的最大利润.
参考答案
一、选择题
1—8:ABDBCBBD
二、填空题
9.答案为:x<2.
10.答案为:1或3.
11.答案为:7.
12.答案为:(,0)或(1,0).
三、解答题
13.【解答】解:(1)∵y﹣3与x+5成正比,
∴设y﹣3=k(x+5),
∵x=2时,y=1,
∴1﹣3=(2+5)k,
∴,
∴,
∴;
(2)当y=4时,
∴
即,
∴.
14.【解答】解:(1)∵y随x的增大而减小,
∴4+2m<0,
即m<﹣2,
当m<﹣2时,y随x的增大而减小.
(2)∵函数图象与y轴的交点在x轴下方,
∴m﹣4<0且4+2m≠0,
即m<4且m≠﹣2,
∴当m<4且m≠﹣2时,函数图象与y轴交点在x轴下方.
(3)若m=﹣1时,
则一次函数解析式为y=2x﹣5,
当函数图象与x轴相交,
∵交点纵坐标为0,
∴0=2x﹣5,即x,
∴此函数图象与x轴的交点坐标为(,0).
15.【解答】解:(1)在一次函数yx+2中,当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
∴S△AOB4;
(2)∵点C与点A关于y轴对称.
∴C(4,0),
如图,连接OP,
设点P(m,)(m>0),
S四边形OBPC=S△BOP+S△POC()=2m+4,
S△APC()=2m+8,
∵S四边形OBPC,
∴2m+4(2m+8),解得m=2.
∴P(2,3).
16.【解答】解:(1)∵y=﹣2x+3过P(n,﹣2).
∴﹣2=﹣2n+3,
解得:n,
∴P(,﹣2),
∵yx+m的图象过P(,﹣2).
∴﹣2m,
解得:m;
(2)不等式x+m>﹣2x+3的解集为x;
(3)∵当y=﹣2x+3中,x=0时,y=3,
∴A(0,3),
∵当yx中,x=0时,y,
∴B(0,),
∴AB=3;
∴△ABP的面积:AB.
17.【解答】解:(1)把M(1,2)代入y=kx得k=2;
把M(1,2)代入yx+b得2b,解得b;
当y=0时,x0,解得x=5,则A(5,0),
所以不等式0的解集为1≤x≤5;
(2)当x=0时,yx,则B(0,),
∴OB,
设P(m,0),则C(m,m),D(m,2m),
∵2CD=OB,
∴2|m2m|,
解得m或,
∴点P的坐标为P (,0)或 (,0).
18.【解答】解;(1)设购进电冰箱x台,这100台家电的销售利润为y元,
根据题意有:y=(1600﹣1500)x+(1400﹣1200)(100﹣x),
整理,得:y=20000﹣100x.
∴y与x之间的函数关系式为y=20000﹣100x;
(2)∵购进空调数量不超过电冰箱数量的2倍,
∴100﹣x≤2x,
解得:.
∵总利润不低于16400元,
∴y≥16400,即20000﹣100x≥16400,
解得:x≤36,
∴.
∵x为整数,
∴x的取值可以为34,35,36,
∴购买方案共有3种.
(3)根据题意有:y=[1600﹣(1500﹣a)]x+(1400﹣1200)(100﹣x),
整理,得:y=(a﹣100)x+20000.
当0<a<100时,a﹣100<0,
∴此时y随x的增大而减小,
∴当x=34时,y最大,ymax=(a﹣100)×34+20000=34a+16600;
当100<a<150时,a﹣100>0,
∴此时y随x的增大而增大,
∴当x=36时,y最大,ymax=(a﹣100)×36+20000=36a+16400;
当a=100时,y=20000.
∴最大利润为(36a+16400)元.
21世纪教育网(www.21cnjy.com)
