中考数学复习专项训练八---网格中的图形变化课件(16张PPT)
文档属性
| 名称 | 中考数学复习专项训练八---网格中的图形变化课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 603.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 18:02:27 | ||
图片预览






文档简介
(共16张PPT)
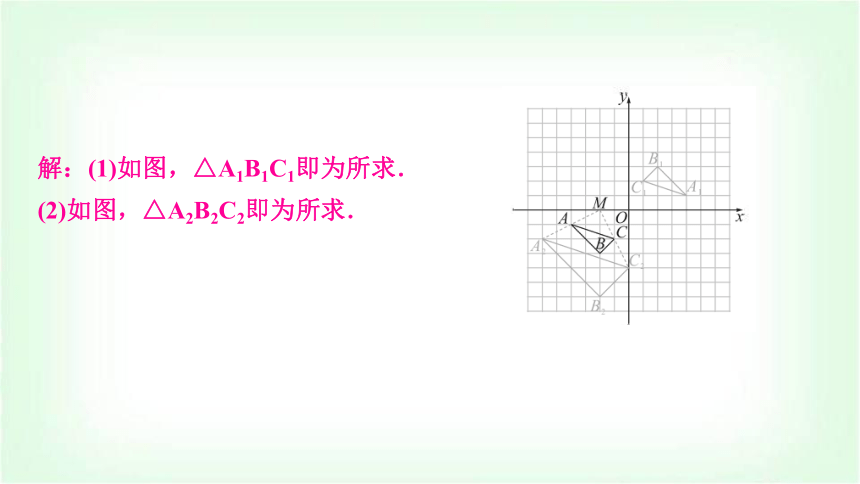
1.(2024·大武口区模拟)如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形),图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)以M(-2,0)为位似中心,在网格中画出△ABC同侧的位似图形△A2B2C2,使△A2B2C2与△ABC的相似比为2∶1.
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
2.(2023·龙东)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度,再向右平移1个单位长度,得到△A1B1C1,请画出△A1B1C1;
(2)请画出△ABC关于y轴对称的△A2B2C2;
(3)将△A2B2C2绕原点O顺时针旋转90°,得到△A3B3C3,求线段A2C2在旋转过程中扫过的面积(结果保留π).
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
3.如图在5×5的正方形网格中,每个小正方形的顶点称为格点.点A,点B都在格点上,按下列要求画图.
(1)在图①中,以AB为一边画△ABC,使点C在格点上,且△ABC是轴对称图形;
(2)在图②中,以AB为一腰画等腰三角形,使点C在格点上;
(3)在图③中,以AB为底边画等腰三角形,使点C在格点上.
解:(1)如图①,△ABC为所作.
(2)如图②,△ABC为所作.
(3)如图③,△ABC为所作.
4.图①,图②,图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A,B均在格点上.按要求作图,所画图形的顶点均在格点上.
(1)在图①中,画等腰三角形ABC,使其面积为3;
(2)在图②中,画等腰直角三角形ABD,使其面积为5;
(3)在图③中,画 ABEF,使∠ABE=135°.
A
解:(1)如图,△ABC即为所求.
(2)如图,△ABD即为所求.
(3)如图, ABEF即为所求.
5.如图①,图②是由边长为1的小正方形构成的网格,图③是由边长为2的小正方形构成的网格,点A,B均在格点上.
(1)在图①中画出以AB为边的菱形ABCD,且点C和点D均在格点上;在图②中画出以AB为对角线的矩形AEBF,且点E和点F均在格点上(画出一个即可);
(2)在图③中画出 ABCD,点C,D均在小正方形的格点上,且此四边形的面积最大;以AD为腰画等腰三角形ADE,点E在小正方形的格点上(不与点B,C重合),且△ADE的面积为16.
解:(1)如图①中,菱形ABCD即为所求,
如图②中,矩形AEBF即为所求.(答案不唯一)
(2)如图③中,四边形ABCD即为所求,△ADE即为所求.
6.如图,是边长为1的小正方形组成的10×10网格,A,B,C,D,E,F均在格点上,下列说法正确的是 (选填序号).
①点E与点C关于点B中心对称;
②连接BF,EC,则BF垂直平分EC;
③连接AB,AD,则AB绕点A逆时
针旋转90°可得到AD.
①②
7.如图,是边长为1的小正方形组成的网格,点A,B,C,D,E,F均在格点上,下列结论:
①△ABC与△DEF关于直线成轴对称;
②BC∥EF;
③△ABC与△DEF是中心对称图形.
其中正确结论的序号是 (选填序号).
②③
1.(2024·大武口区模拟)如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形),图中△ABC是格点三角形,点A,B,C的坐标分别是(-4,-1),(-2,-3),(-1,-2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)以M(-2,0)为位似中心,在网格中画出△ABC同侧的位似图形△A2B2C2,使△A2B2C2与△ABC的相似比为2∶1.
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
2.(2023·龙东)如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,-1),B(1,-2),C(3,-3).
(1)将△ABC向上平移4个单位长度,再向右平移1个单位长度,得到△A1B1C1,请画出△A1B1C1;
(2)请画出△ABC关于y轴对称的△A2B2C2;
(3)将△A2B2C2绕原点O顺时针旋转90°,得到△A3B3C3,求线段A2C2在旋转过程中扫过的面积(结果保留π).
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
3.如图在5×5的正方形网格中,每个小正方形的顶点称为格点.点A,点B都在格点上,按下列要求画图.
(1)在图①中,以AB为一边画△ABC,使点C在格点上,且△ABC是轴对称图形;
(2)在图②中,以AB为一腰画等腰三角形,使点C在格点上;
(3)在图③中,以AB为底边画等腰三角形,使点C在格点上.
解:(1)如图①,△ABC为所作.
(2)如图②,△ABC为所作.
(3)如图③,△ABC为所作.
4.图①,图②,图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A,B均在格点上.按要求作图,所画图形的顶点均在格点上.
(1)在图①中,画等腰三角形ABC,使其面积为3;
(2)在图②中,画等腰直角三角形ABD,使其面积为5;
(3)在图③中,画 ABEF,使∠ABE=135°.
A
解:(1)如图,△ABC即为所求.
(2)如图,△ABD即为所求.
(3)如图, ABEF即为所求.
5.如图①,图②是由边长为1的小正方形构成的网格,图③是由边长为2的小正方形构成的网格,点A,B均在格点上.
(1)在图①中画出以AB为边的菱形ABCD,且点C和点D均在格点上;在图②中画出以AB为对角线的矩形AEBF,且点E和点F均在格点上(画出一个即可);
(2)在图③中画出 ABCD,点C,D均在小正方形的格点上,且此四边形的面积最大;以AD为腰画等腰三角形ADE,点E在小正方形的格点上(不与点B,C重合),且△ADE的面积为16.
解:(1)如图①中,菱形ABCD即为所求,
如图②中,矩形AEBF即为所求.(答案不唯一)
(2)如图③中,四边形ABCD即为所求,△ADE即为所求.
6.如图,是边长为1的小正方形组成的10×10网格,A,B,C,D,E,F均在格点上,下列说法正确的是 (选填序号).
①点E与点C关于点B中心对称;
②连接BF,EC,则BF垂直平分EC;
③连接AB,AD,则AB绕点A逆时
针旋转90°可得到AD.
①②
7.如图,是边长为1的小正方形组成的网格,点A,B,C,D,E,F均在格点上,下列结论:
①△ABC与△DEF关于直线成轴对称;
②BC∥EF;
③△ABC与△DEF是中心对称图形.
其中正确结论的序号是 (选填序号).
②③
同课章节目录
