【期中押题卷】广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷北师大版(含解析)
文档属性
| 名称 | 【期中押题卷】广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-01 20:58:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷
一.选择题(共9小题,满分18分,每小题2分)
1.(2分)(2024春 信宜市期末)一个水池能蓄水600m3,也就是说这个水池的( )是600m3。
A.表面积 B.重量 C.体积 D.容积
2.(2分)下面左边的图形需要添几个同样大的小正方体才能拼成右边的大长方体?( )
A.3个 B.4个 C.5个
3.(2分)(2023 章丘区)有甲、乙两根绳子,甲绳减去,乙绳减去米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
4.(2分)(2024春 临县期中)下列图形中能围成正方体的是( )
A. B.
C. D.
5.(2分)(2024秋 瑶海区期末)m是一个大于又小于的数,m与它的倒数比较大小,结果是( )
A.m更小 B.m更大 C.相等
6.(2分)(2023 平谷区模拟)如果a×b,a×b×c,那么等于( )
A.1 B. C.1 D.
7.(2分)(2023春 鱼台县期末)用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
8.(2分)(2023春 平度市期末)如图是用27个小正方体拼成的,拿走角上的一个小正方体,它的表面积与原来比较( )
A.变大 B.变小 C.不变
9.(2分)(2020秋 湖里区期中)图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分占空白部分面积的( )
A. B. C. D.
二.填空题(共10小题,满分20分)
10.(4分)(2023秋 安丘市期中)填上合适的单位名称。
一支铅笔约重13 ;
一头牛约重240 ;
鲸鱼体重34 ,每小时游30 。
11.(3分)(2022春 华安县期末)将算式改写成小数加法为 + ,计算结果为 。
12.(1分)(2024 张家口)一个长为15分米、宽为0.6米、高为0.4米的长方体。最多可以切出 个棱长为2分米的小正方体。
13.(3分)(2023秋 辉县市校级月考) =0.3× =4× =1。
14.(2分)(2024秋 城厢区期中)“中国交通的发展日新月异。复兴号动车组的速度高达350千米/时,而磁悬浮列车的时速比复兴号快,堪比飞机,磁悬浮列车的速度是多少?”题目中将 看作了单位“1”,根据题目中的信息写出的数量关系式是 。
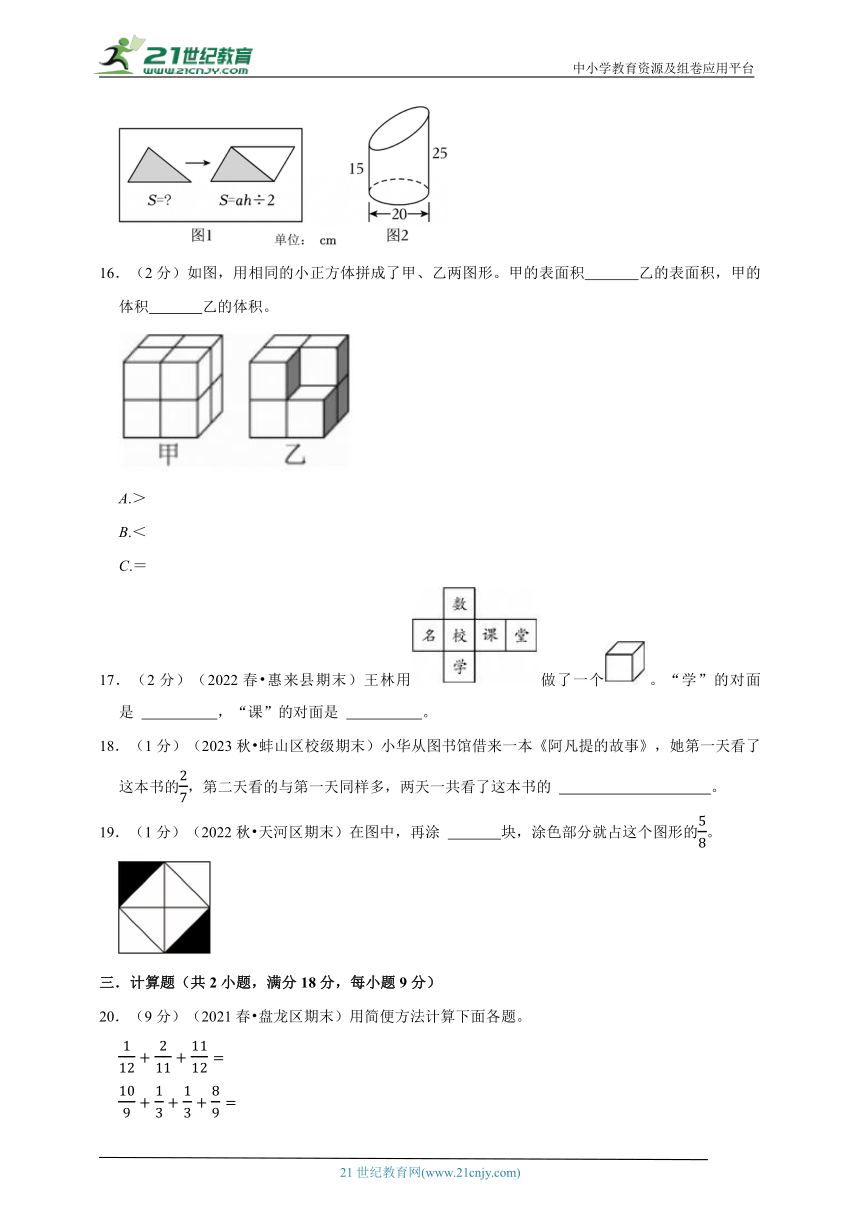
15.(1分)(2024 电白区)我们曾经用如图所示方法解决了求三角形面积的问题,有这样的经验,我能算出图2的几何体体积是 cm3。
16.(2分)如图,用相同的小正方体拼成了甲、乙两图形。甲的表面积 乙的表面积,甲的体积 乙的体积。
A.>
B.<
C.=
17.(2分)(2022春 惠来县期末)王林用做了一个。“学”的对面是 ,“课”的对面是 。
18.(1分)(2023秋 蚌山区校级期末)小华从图书馆借来一本《阿凡提的故事》,她第一天看了这本书的,第二天看的与第一天同样多,两天一共看了这本书的 。
19.(1分)(2022秋 天河区期末)在图中,再涂 块,涂色部分就占这个图形的。
三.计算题(共2小题,满分18分,每小题9分)
20.(9分)(2021春 盘龙区期末)用简便方法计算下面各题。
21.(9分)(2023秋 汝州市校级月考)解下列方程。
3x﹣1.4=4.6
四.解答题(共5小题,满分20分)
22.(3分)(2021春 广元期末)一杯纯牛奶,聪聪喝了杯后,觉得有些凉,就兑满了热水,又喝了杯。他一共喝了多少杯纯牛奶?多少杯水?(用画图的方式解答)
23.(3分)(2023秋 房山区期末)画图表示的过程和结果。
24.(4分)(2022秋 闽清县期末)哪些形状是用4个拼成的?在括号里画“√”。
25.(5分)(2023 南京)我们在小学阶段学过了正方体、长方体、圆柱体和圆锥体的体积,具体如下:
以后,当我研究“球的体积”时,我对这节课的学习目标可能有如下的想法:
(1)我会提出:“如何计算球的体积?”,还会提出: ?
(2)我会提出“怎样推导球的体积?”,我觉得可以用 的方法。
(3)通过观察上面几何形体和体积计算公式,我发现:几何形体的体积都是3个变量的乘积。所以当球的半径为r时,我猜想,球的体积可能是 。
26.(5分)(2021秋 互助县期末)如图,有6个△,把其中涂黑色。
五.应用题(共4小题,满分24分)
27.(5分)(2024春 天河区期末)某森林公园的林木面积是公顷。这个森林公园的草地面积和林木面积一共是多少公顷?
28.(5分)(2023秋 临漳县期中)青藏铁路是世界上海拔最高、线路最长的高原铁路,西宁至拉萨的铁路全长1956千米。一列火车从西宁开出,已经行了全程的,距离拉萨还有多少千米?
29.(5分)(2023春 蠡县期末)一个封闭的长方体玻璃容器(玻璃厚度不计)长4分米,宽3分米,高8分米,里面水深5分米(如图①)。现在以这个容器的右侧为底,侧放在桌面上(如图②)。这时水深多少分米?
30.(9分)(2023春 永嘉县期末)先从一张长40厘米,宽35厘米的长方形铁皮的四个角各剪去一个边长是5厘米的正方形,然后做成一个无盖的长方体盒子。
(1)这个盒子用了多少平方厘米铁皮?
(2)这个铁皮盒子的容积是多少立方厘米?
广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 D B A B A C C C A
一.选择题(共9小题,满分18分,每小题2分)
1.(2分)(2024春 信宜市期末)一个水池能蓄水600m3,也就是说这个水池的( )是600m3。
A.表面积 B.重量 C.体积 D.容积
【考点】体积、容积及其单位.
【专题】综合判断题;应用意识.
【答案】D
【分析】根据容积的意义,物体所能容纳物体的体积是这个物体的容积,一个水池能蓄水600m3,即这个蓄水池能容纳水的体积是600m3,因此,我们就说这个水池的容积是600m3。
【解答】解:一个水池能蓄水600m3,我们就说这个水池的容积是600m3。
故选:D。
【点评】此题是考查容积的意义,属于基本概念,要记住。
2.(2分)下面左边的图形需要添几个同样大的小正方体才能拼成右边的大长方体?( )
A.3个 B.4个 C.5个
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】B
【分析】根据图示可知,上层添了3个,中间一层添了1个,据此解答。
【解答】解:3+1=4(个)
答:左边的图形需要添4个同样大的小正方体才能拼成右边的大长方体。
故选:B。
【点评】本题主要考查几何图形的计数。
3.(2分)(2023 章丘区)有甲、乙两根绳子,甲绳减去,乙绳减去米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
【考点】分数四则复合应用题;分数的意义和读写.
【专题】应用意识.
【答案】A
【分析】先用2除以(1),求出甲绳长;再用2加上,求出乙绳长;最后比较两根绳子的长短即可。
【解答】解:2÷(1)
=2
=2.5(米)
22.2(米)
2.5>2.2
答:甲绳比乙绳长。
故选:A。
【点评】解答本题需明确:表示的是分率,米表示具体的长度。
4.(2分)(2024春 临县期中)下列图形中能围成正方体的是( )
A. B.
C. D.
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】B
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能围成正方体,哪个图形不属于正方体展开图,不能围成正方体。
【解答】解:A、不属于正方体展开图,不能围成正方体;
B、属于正方体展开图的“1﹣4﹣1”型,能围成正方体;
C、不属于正方体展开图,不能围成正方体;
D、不属于正方体展开图,不能围成正方体。
故选:B。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
5.(2分)(2024秋 瑶海区期末)m是一个大于又小于的数,m与它的倒数比较大小,结果是( )
A.m更小 B.m更大 C.相等
【考点】倒数的认识;分数大小的比较.
【专题】分数和百分数;数据分析观念.
【答案】A
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。
求一个分数的倒数,只需把这个分数的分子和分母交换位置,即它的倒数。
【解答】解:m是一个大于又小于的数,m与它的倒数比较m更小。
故选:A。
【点评】本题考查了求一个分数的倒数的方法。
6.(2分)(2023 平谷区模拟)如果a×b,a×b×c,那么等于( )
A.1 B. C.1 D.
【考点】分数除法应用题.
【专题】分数百分数应用题;应用意识.
【答案】C
【分析】由题意可知,c=(a×b×c)÷(a×b),所以1÷c,据此作答即可。
【解答】解:
1
故选:C。
【点评】解答此题的关键是根据a与b的积已知,求出c的值,再用除法计算。
7.(2分)(2023春 鱼台县期末)用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
【考点】长方体的特征.
【专题】数据分析观念.
【答案】C
【分析】因为长方体的棱长总和=(长+宽+高)×4,所以用棱长总和除以4再减去长与宽的和即可,据此解答。
【解答】解:1m=100cm
100÷4﹣(10+5)
=25﹣15
=10(厘米)
答:用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高10厘米的长方体。
故选:C。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用。
8.(2分)(2023春 平度市期末)如图是用27个小正方体拼成的,拿走角上的一个小正方体,它的表面积与原来比较( )
A.变大 B.变小 C.不变
【考点】简单的立方体切拼问题;长方体和正方体的表面积.
【专题】空间观念;几何直观.
【答案】C
【分析】从顶点上取走一个小长方体后,体积明显的减少了;但表面减少了小正方体3个面的面积,同时又增加了3个面,然后据此解答即可。
【解答】解:表面积减少了小正方体3个不同的面的面积,同时又增加了小正方体3个面的面积,即相当于相互抵消,实际上表面积不变,所以体积减少,表面积不变。
故选:C。
【点评】本题关键是理解挖去的小正方体是在什么位置,注意知识的拓展,如果从顶点挖而且没有挖透那么体积变小,表面积不变;如果从一个面的中间挖而且没有挖透那么体积变小,表面积变大。
9.(2分)(2020秋 湖里区期中)图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分占空白部分面积的( )
A. B. C. D.
【考点】分数的意义和读写.
【专题】分数和百分数;数据分析观念.
【答案】A
【分析】设每个小长方形的长为a,宽为b,于是可以分别求出阴影部分和长方形的面积,进而求出阴影部分与空白部分面积的最简整数比。
【解答】解:假设每个小长方形的长为a,宽为b,
则长方形的面积是:a×4b=4ab;
阴影部分的面积是:(a×b÷2)×3=1.5ab;
空白部分的面积是:4ab﹣1.5ab=2.5ab;
所以阴影部分与空白部分面积的最简整数比是:
1.5ab:2.5ab=3:5;
答:阴影部分占空白部分面积的。
故选:A。
【点评】此题主要考查三角形和长方形的面积的计算方法的灵活应用。
二.填空题(共10小题,满分20分)
10.(4分)(2023秋 安丘市期中)填上合适的单位名称。
一支铅笔约重13 克 ;
一头牛约重240 千克 ;
鲸鱼体重34 吨 ,每小时游30 千米 。
【考点】根据情景选择合适的计量单位.
【专题】应用意识.
【答案】克;千克;吨;千米。
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:一支铅笔约重13克;
一头牛约重240千克;
鲸鱼体重34吨,每小时游30千米。
故答案为:克;千克;吨;千米。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
11.(3分)(2022春 华安县期末)将算式改写成小数加法为 0.25 + 0.025 ,计算结果为 0.275 。
【考点】小数与分数的互化;小数的加法和减法.
【专题】运算能力.
【答案】0.25;0.025;0.275。
【分析】根据小数的意义,先把和化成小数后,再计算结果。
【解答】解:
=0.25+0.025
=0.275
答:将算式改写成小数加法为0.25+0.025,计算结果为0.275。
故答案为:0.25;0.025;0.275。
【点评】本题解题关键是理解小数的意义,熟练掌握小数加法的计算方法。
12.(1分)(2024 张家口)一个长为15分米、宽为0.6米、高为0.4米的长方体。最多可以切出 42 个棱长为2分米的小正方体。
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】42。
【分析】分别求出沿长、宽、高切,切出小正方体的个数,再相乘即可解答。
【解答】解:15÷2=7(个)……1(分米)
0.6米=6分米
6÷2=3(个)
0.4米=4分米
4÷2=2(个)
7×3×2
=21×2
=42(个)
答:最多可以切出42个棱长为2分米的小正方体。
故答案为:42。
【点评】此题考查长方体和正方体的体积。解答时注意单位要统一再计算。
13.(3分)(2023秋 辉县市校级月考) =0.3× =4× 0.25 =1。
【考点】倒数的认识.
【专题】分数和百分数;数据分析观念.
【答案】,,0.25。
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。
【解答】解: 0.34×0.25=1
故答案为:,,0.25。
【点评】此题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数。
14.(2分)(2024秋 城厢区期中)“中国交通的发展日新月异。复兴号动车组的速度高达350千米/时,而磁悬浮列车的时速比复兴号快,堪比飞机,磁悬浮列车的速度是多少?”题目中将 复兴号动车组的速度 看作了单位“1”,根据题目中的信息写出的数量关系式是 磁悬浮列车的时速=复兴号动车组的速度×(1) 。
【考点】分数乘法应用题.
【专题】应用题;应用意识.
【答案】复兴号动车组的速度;磁悬浮列车的时速=复兴号动车组的速度×(1)。
【分析】依据题意可知,把复兴号动车组的速度看作单位“1”,磁悬浮列车的时速=复兴号动车组的速度×(1),由此解答本题即可。
【解答】解:把复兴号动车组的速度看作单位“1”,根据题目中的信息写出的数量关系式:磁悬浮列车的时速=复兴号动车组的速度×(1)。
故答案为:复兴号动车组的速度;磁悬浮列车的时速=复兴号动车组的速度×(1)。
【点评】解决本题的关键是找出题中数量关系。
15.(1分)(2024 电白区)我们曾经用如图所示方法解决了求三角形面积的问题,有这样的经验,我能算出图2的几何体体积是 6280 cm3。
【考点】圆柱的体积;长方体和正方体的体积.
【专题】应用题;应用意识.
【答案】6280。
【分析】找两个一模一样大的,几何体上下拼接在一起就会变成一个底面直径为20厘米,高为15+25=40(厘米)的圆柱体,圆柱体的体积是底面积乘高,而该几何体的体积则是圆柱体体积的一半,即可求出该几何体的体积。
【解答】解:如图
20÷2=10厘米
3.14×10×10×(25+15)
=3.14×100×40
=12560(立方厘米)
12560÷2=6280(立方厘米)
故答案为:6280。
【点评】解答此题首先先画图帮助理解题意,然后利用公式V=Sh解答。
16.(2分)如图,用相同的小正方体拼成了甲、乙两图形。甲的表面积 C 乙的表面积,甲的体积 A 乙的体积。
A.>
B.<
C.=
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【专题】几何直观.
【答案】C,A。
【分析】观察图形可知,甲的表面积等于24个小正方形的面积之和,乙的表面积也等于24个小正方形的面积之和,据此比较两个图形的表面积的大小;甲的体积等于8个小正方体的体积之和,乙的体积等于7个小正方体的体积之和,据此比较两个图形的体积的大小。
【解答】解:甲的表面积等于24个小正方形的面积之和,乙的表面积也等于24个小正方形的面积之和,所以两个图形的表面积相等;甲的体积等于8个小正方体的体积之和,乙的体积等于7个小正方体的体积之和,所以甲的体积大于乙的体积。
故答案为:C,A。
【点评】解答本题需熟练掌握表面积和体积的意义,准确识图是关键。
17.(2分)(2022春 惠来县期末)王林用做了一个。“学”的对面是 “教” ,“课”的对面是 “名” 。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】“数”,“名”。
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,“名”与“课”相对,“校”与“堂”相对,“数”与“学”相对。
【解答】解:王林用做了一个。“学”的对面是“数”,“课”的对面是“名”。
故答案为:“数”,“名”。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
18.(1分)(2023秋 蚌山区校级期末)小华从图书馆借来一本《阿凡提的故事》,她第一天看了这本书的,第二天看的与第一天同样多,两天一共看了这本书的 。
【考点】分数加减法应用题.
【专题】应用题;应用意识.
【答案】。
【分析】第二天看的与第一天同样多,则第二天也看了这本书的。用()求出两天一共看了这本书的几分之几。
【解答】解:
答:两天一共看了这本书的。
故答案为:。
【点评】此题考查了运用分数加法解决实际问题。
19.(1分)(2022秋 天河区期末)在图中,再涂 3 块,涂色部分就占这个图形的。
【考点】分数的意义和读写.
【专题】分数和百分数;数据分析观念.
【答案】3。
【分析】将这个图形平均分成8块,其中1块占这个图形的,5块占这个图形的。题图中已经涂了2块,还需要涂(5﹣2)块。据此解答。
【解答】解:5﹣2=3(块)
则再涂3块,涂色部分就占这个图形的。
故答案为:3。
【点评】此题考查分数的认识。把一个整体平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。
三.计算题(共2小题,满分18分,每小题9分)
20.(9分)(2021春 盘龙区期末)用简便方法计算下面各题。
【考点】分数的加减混合运算.
【专题】运算能力.
【答案】1,2。
【分析】(1)运用加法交换律进行简算;
(2)运用加法交换律、结合律进行简算。
【解答】解:(1)
=1
=1
(2)
=()+()
=2
=2
【点评】此题考查了加法交换律、结合律的灵活运用。
21.(9分)(2023秋 汝州市校级月考)解下列方程。
3x﹣1.4=4.6
【考点】分数方程求解;小数方程求解.
【专题】简易方程;运算能力.
【答案】x=30;x=16;x=2。
【分析】(1)根据等式的性质,两边同时乘即可;
(2)首先根据等式的性质,两边同时减去1,然后两边同时乘即可;
(3)首先根据等式的性质,两边同时加上1.4,然后两边再同时除以3即可。
【解答】解:(1)
x25
x=30
(2)
1x﹣1=13﹣1
x=12
x12
x=16
(3)3x﹣1.4=4.6
3x﹣1.4+1.4=4.6+1.4
3x=6
3x÷3=6÷3
x=2
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
四.解答题(共5小题,满分20分)
22.(3分)(2021春 广元期末)一杯纯牛奶,聪聪喝了杯后,觉得有些凉,就兑满了热水,又喝了杯。他一共喝了多少杯纯牛奶?多少杯水?(用画图的方式解答)
【考点】异分母分数加减法.
【专题】数据分析观念;运算能力.
【答案】杯纯牛奶,杯水。
【分析】由题意可知:先喝的这是牛奶,还剩下(1)的牛奶,喝了杯后,觉得有些凉,就兑满了热水。说明加入了的水,这时水杯是满的,聪聪又喝了杯,那么聪聪第二次喝的牛奶就是剩下的(1)的,所以第二次喝的牛奶是(1)杯,两次一共喝的牛奶是杯加上(1)杯;求喝了多少杯水,杯子里的水一共有,第二次喝了杯,则喝的水就是杯的,由此即可解答。
【解答】解:作图如下:
牛奶:
(杯)
水:(杯)
答:他一共喝了杯纯牛奶,杯水。
【点评】此题考查的是分数乘法与分数加减法的混合运算。
23.(3分)(2023秋 房山区期末)画图表示的过程和结果。
【考点】分数乘分数.
【专题】运算能力.
【答案】;。
【分析】根据分数乘法的意义,先表示一个长方形的,再表示的,据此画图表示的过程和结果。
【解答】解:
【点评】本题解题的关键是熟练掌握分数乘法的计算方法。
24.(4分)(2022秋 闽清县期末)哪些形状是用4个拼成的?在括号里画“√”。
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】
【分析】根据图示,图一由3个小正方体拼成,图二和图三都是由4个小正方体拼成,据此解答即可。
【解答】解:解答如下:
【点评】本题考查了立体图形的拼组知识,结合题意分析解答即可。
25.(5分)(2023 南京)我们在小学阶段学过了正方体、长方体、圆柱体和圆锥体的体积,具体如下:
以后,当我研究“球的体积”时,我对这节课的学习目标可能有如下的想法:
(1)我会提出:“如何计算球的体积?”,还会提出: 如何求球的表面积 ?
(2)我会提出“怎样推导球的体积?”,我觉得可以用 转化 的方法。
(3)通过观察上面几何形体和体积计算公式,我发现:几何形体的体积都是3个变量的乘积。所以当球的半径为r时,我猜想,球的体积可能是 Vπr3 。
【考点】探索某些实物体积的测量方法.
【专题】综合填空题;几何直观.
【答案】(1)如何求球的表面积;(答案不唯一)
(2)转化;
(3)Vπr3。
【分析】(1)还会提出:如何求球的表面积?(答案不唯一)
(2)把球放入内直径和高与球直径相等的圆柱形容器里,加满水,分别记录取出球前后,容器内水的高度,由此计算球的体积;(答案不唯一)
(3)依据题意推算球的体积。(答案不唯一)
【解答】解:由分析可知,(1)还会提出:如何求球的表面积?(答案不唯一)
(2)可以用转化的方法。
(3)球的体积可能是Vπr3
故答案为:(1)如何求球的表面积;(答案不唯一)(2)转化;(3)Vπr3。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
26.(5分)(2021秋 互助县期末)如图,有6个△,把其中涂黑色。
【考点】分数乘法应用题.
【专题】应用意识.
【答案】。
【分析】一共有6个△,把三角形的总数看成单位“1”,用6乘即可求出需要涂黑色的个数。
【解答】解:64(个)
答:需要涂黑4个三角形。
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法求解。
五.应用题(共4小题,满分24分)
27.(5分)(2024春 天河区期末)某森林公园的林木面积是公顷。这个森林公园的草地面积和林木面积一共是多少公顷?
【考点】分数加减法应用题.
【专题】应用题;应用意识.
【答案】公顷。
【分析】已知林木面积是公顷,用林木面积减去就是草地面积,然后把林木面积和草地面积相加即可解答此题。
【解答】解:
(公顷)
答:这个森林公园的草地面积和林木面积一共是公顷。
【点评】解答此题的关键是要先求出草地的面积,然后把林木面积和草地面积相加即可。
28.(5分)(2023秋 临漳县期中)青藏铁路是世界上海拔最高、线路最长的高原铁路,西宁至拉萨的铁路全长1956千米。一列火车从西宁开出,已经行了全程的,距离拉萨还有多少千米?
【考点】分数乘法应用题.
【专题】应用题;应用意识.
【答案】326千米。
【分析】距离拉萨的距离=铁路全长×(1),由此列式计算即可。
【解答】解:1956×(1)
=1956
=326(千米)
答:距离拉萨还有326千米。
【点评】解决本题的关键是找出题中的数量关系。
29.(5分)(2023春 蠡县期末)一个封闭的长方体玻璃容器(玻璃厚度不计)长4分米,宽3分米,高8分米,里面水深5分米(如图①)。现在以这个容器的右侧为底,侧放在桌面上(如图②)。这时水深多少分米?
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】2.5分米。
【分析】根据长方体体积公式V=abh,计算出图1中水的体积,也就是图2中水的体积;根据长方体体积公式可得h=V÷a÷b,据此计算出图2的水深。
【解答】解:4×3×5÷8÷3
=12×5÷8÷3
=60÷8÷3
=7.5÷3
=2.5(分米)
答:这时水深2.5分米。
【点评】本题主要考查长方体体积计算公式的应用,熟练掌握长方体体积公式是解答本题的关键。
30.(9分)(2023春 永嘉县期末)先从一张长40厘米,宽35厘米的长方形铁皮的四个角各剪去一个边长是5厘米的正方形,然后做成一个无盖的长方体盒子。
(1)这个盒子用了多少平方厘米铁皮?
(2)这个铁皮盒子的容积是多少立方厘米?
【考点】长方体、正方体表面积与体积计算的应用.
【专题】运算能力.
【答案】(1)1300平方厘米;(2)3750立方厘米。
【分析】(1)观察图形可知,折成的长方体的长为40﹣5×2=30(厘米),宽为35﹣5×2=25(厘米),高是5厘米,铁皮的面积就是长方体的五个面的面积,长方体的五个面的面积=长×宽+(长×高+宽×高)×2,据此计算即可;
(2)根据长方体的容积公式:V=abh,据此代入数值进行计算即可。
【解答】解:(1)40﹣5×2
=40﹣10
=30(厘米)
35﹣5×2
=35﹣10
=25(厘米)
30×25+(30×5+25×5)×2
=750+(150+125)×2
=750+275×2
=750+550
=1300(平方厘米)
答:这个盒子用了1300平方厘米铁皮。
(2)30×25×5
=750×5
=3750(立方厘米)
答:这个铁皮盒子的容积是3750立方厘米。
【点评】本题考查长方体的表面积和容积,熟记公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷
一.选择题(共9小题,满分18分,每小题2分)
1.(2分)(2024春 信宜市期末)一个水池能蓄水600m3,也就是说这个水池的( )是600m3。
A.表面积 B.重量 C.体积 D.容积
2.(2分)下面左边的图形需要添几个同样大的小正方体才能拼成右边的大长方体?( )
A.3个 B.4个 C.5个
3.(2分)(2023 章丘区)有甲、乙两根绳子,甲绳减去,乙绳减去米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
4.(2分)(2024春 临县期中)下列图形中能围成正方体的是( )
A. B.
C. D.
5.(2分)(2024秋 瑶海区期末)m是一个大于又小于的数,m与它的倒数比较大小,结果是( )
A.m更小 B.m更大 C.相等
6.(2分)(2023 平谷区模拟)如果a×b,a×b×c,那么等于( )
A.1 B. C.1 D.
7.(2分)(2023春 鱼台县期末)用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
8.(2分)(2023春 平度市期末)如图是用27个小正方体拼成的,拿走角上的一个小正方体,它的表面积与原来比较( )
A.变大 B.变小 C.不变
9.(2分)(2020秋 湖里区期中)图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分占空白部分面积的( )
A. B. C. D.
二.填空题(共10小题,满分20分)
10.(4分)(2023秋 安丘市期中)填上合适的单位名称。
一支铅笔约重13 ;
一头牛约重240 ;
鲸鱼体重34 ,每小时游30 。
11.(3分)(2022春 华安县期末)将算式改写成小数加法为 + ,计算结果为 。
12.(1分)(2024 张家口)一个长为15分米、宽为0.6米、高为0.4米的长方体。最多可以切出 个棱长为2分米的小正方体。
13.(3分)(2023秋 辉县市校级月考) =0.3× =4× =1。
14.(2分)(2024秋 城厢区期中)“中国交通的发展日新月异。复兴号动车组的速度高达350千米/时,而磁悬浮列车的时速比复兴号快,堪比飞机,磁悬浮列车的速度是多少?”题目中将 看作了单位“1”,根据题目中的信息写出的数量关系式是 。
15.(1分)(2024 电白区)我们曾经用如图所示方法解决了求三角形面积的问题,有这样的经验,我能算出图2的几何体体积是 cm3。
16.(2分)如图,用相同的小正方体拼成了甲、乙两图形。甲的表面积 乙的表面积,甲的体积 乙的体积。
A.>
B.<
C.=
17.(2分)(2022春 惠来县期末)王林用做了一个。“学”的对面是 ,“课”的对面是 。
18.(1分)(2023秋 蚌山区校级期末)小华从图书馆借来一本《阿凡提的故事》,她第一天看了这本书的,第二天看的与第一天同样多,两天一共看了这本书的 。
19.(1分)(2022秋 天河区期末)在图中,再涂 块,涂色部分就占这个图形的。
三.计算题(共2小题,满分18分,每小题9分)
20.(9分)(2021春 盘龙区期末)用简便方法计算下面各题。
21.(9分)(2023秋 汝州市校级月考)解下列方程。
3x﹣1.4=4.6
四.解答题(共5小题,满分20分)
22.(3分)(2021春 广元期末)一杯纯牛奶,聪聪喝了杯后,觉得有些凉,就兑满了热水,又喝了杯。他一共喝了多少杯纯牛奶?多少杯水?(用画图的方式解答)
23.(3分)(2023秋 房山区期末)画图表示的过程和结果。
24.(4分)(2022秋 闽清县期末)哪些形状是用4个拼成的?在括号里画“√”。
25.(5分)(2023 南京)我们在小学阶段学过了正方体、长方体、圆柱体和圆锥体的体积,具体如下:
以后,当我研究“球的体积”时,我对这节课的学习目标可能有如下的想法:
(1)我会提出:“如何计算球的体积?”,还会提出: ?
(2)我会提出“怎样推导球的体积?”,我觉得可以用 的方法。
(3)通过观察上面几何形体和体积计算公式,我发现:几何形体的体积都是3个变量的乘积。所以当球的半径为r时,我猜想,球的体积可能是 。
26.(5分)(2021秋 互助县期末)如图,有6个△,把其中涂黑色。
五.应用题(共4小题,满分24分)
27.(5分)(2024春 天河区期末)某森林公园的林木面积是公顷。这个森林公园的草地面积和林木面积一共是多少公顷?
28.(5分)(2023秋 临漳县期中)青藏铁路是世界上海拔最高、线路最长的高原铁路,西宁至拉萨的铁路全长1956千米。一列火车从西宁开出,已经行了全程的,距离拉萨还有多少千米?
29.(5分)(2023春 蠡县期末)一个封闭的长方体玻璃容器(玻璃厚度不计)长4分米,宽3分米,高8分米,里面水深5分米(如图①)。现在以这个容器的右侧为底,侧放在桌面上(如图②)。这时水深多少分米?
30.(9分)(2023春 永嘉县期末)先从一张长40厘米,宽35厘米的长方形铁皮的四个角各剪去一个边长是5厘米的正方形,然后做成一个无盖的长方体盒子。
(1)这个盒子用了多少平方厘米铁皮?
(2)这个铁皮盒子的容积是多少立方厘米?
广东省深圳市2024-2025学年五年级下学期期中模拟预测数学试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 D B A B A C C C A
一.选择题(共9小题,满分18分,每小题2分)
1.(2分)(2024春 信宜市期末)一个水池能蓄水600m3,也就是说这个水池的( )是600m3。
A.表面积 B.重量 C.体积 D.容积
【考点】体积、容积及其单位.
【专题】综合判断题;应用意识.
【答案】D
【分析】根据容积的意义,物体所能容纳物体的体积是这个物体的容积,一个水池能蓄水600m3,即这个蓄水池能容纳水的体积是600m3,因此,我们就说这个水池的容积是600m3。
【解答】解:一个水池能蓄水600m3,我们就说这个水池的容积是600m3。
故选:D。
【点评】此题是考查容积的意义,属于基本概念,要记住。
2.(2分)下面左边的图形需要添几个同样大的小正方体才能拼成右边的大长方体?( )
A.3个 B.4个 C.5个
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】B
【分析】根据图示可知,上层添了3个,中间一层添了1个,据此解答。
【解答】解:3+1=4(个)
答:左边的图形需要添4个同样大的小正方体才能拼成右边的大长方体。
故选:B。
【点评】本题主要考查几何图形的计数。
3.(2分)(2023 章丘区)有甲、乙两根绳子,甲绳减去,乙绳减去米,两根绳子都剩下2米,比较两根绳子原来的长度,正确的是( )
A.甲比乙长 B.乙比甲长
C.两根绳子一样长 D.无法比较
【考点】分数四则复合应用题;分数的意义和读写.
【专题】应用意识.
【答案】A
【分析】先用2除以(1),求出甲绳长;再用2加上,求出乙绳长;最后比较两根绳子的长短即可。
【解答】解:2÷(1)
=2
=2.5(米)
22.2(米)
2.5>2.2
答:甲绳比乙绳长。
故选:A。
【点评】解答本题需明确:表示的是分率,米表示具体的长度。
4.(2分)(2024春 临县期中)下列图形中能围成正方体的是( )
A. B.
C. D.
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】B
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能围成正方体,哪个图形不属于正方体展开图,不能围成正方体。
【解答】解:A、不属于正方体展开图,不能围成正方体;
B、属于正方体展开图的“1﹣4﹣1”型,能围成正方体;
C、不属于正方体展开图,不能围成正方体;
D、不属于正方体展开图,不能围成正方体。
故选:B。
【点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
5.(2分)(2024秋 瑶海区期末)m是一个大于又小于的数,m与它的倒数比较大小,结果是( )
A.m更小 B.m更大 C.相等
【考点】倒数的认识;分数大小的比较.
【专题】分数和百分数;数据分析观念.
【答案】A
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。
求一个分数的倒数,只需把这个分数的分子和分母交换位置,即它的倒数。
【解答】解:m是一个大于又小于的数,m与它的倒数比较m更小。
故选:A。
【点评】本题考查了求一个分数的倒数的方法。
6.(2分)(2023 平谷区模拟)如果a×b,a×b×c,那么等于( )
A.1 B. C.1 D.
【考点】分数除法应用题.
【专题】分数百分数应用题;应用意识.
【答案】C
【分析】由题意可知,c=(a×b×c)÷(a×b),所以1÷c,据此作答即可。
【解答】解:
1
故选:C。
【点评】解答此题的关键是根据a与b的积已知,求出c的值,再用除法计算。
7.(2分)(2023春 鱼台县期末)用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
【考点】长方体的特征.
【专题】数据分析观念.
【答案】C
【分析】因为长方体的棱长总和=(长+宽+高)×4,所以用棱长总和除以4再减去长与宽的和即可,据此解答。
【解答】解:1m=100cm
100÷4﹣(10+5)
=25﹣15
=10(厘米)
答:用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高10厘米的长方体。
故选:C。
【点评】此题考查的目的是理解掌握长方体的特征,以及长方体棱长总和公式的灵活运用。
8.(2分)(2023春 平度市期末)如图是用27个小正方体拼成的,拿走角上的一个小正方体,它的表面积与原来比较( )
A.变大 B.变小 C.不变
【考点】简单的立方体切拼问题;长方体和正方体的表面积.
【专题】空间观念;几何直观.
【答案】C
【分析】从顶点上取走一个小长方体后,体积明显的减少了;但表面减少了小正方体3个面的面积,同时又增加了3个面,然后据此解答即可。
【解答】解:表面积减少了小正方体3个不同的面的面积,同时又增加了小正方体3个面的面积,即相当于相互抵消,实际上表面积不变,所以体积减少,表面积不变。
故选:C。
【点评】本题关键是理解挖去的小正方体是在什么位置,注意知识的拓展,如果从顶点挖而且没有挖透那么体积变小,表面积不变;如果从一个面的中间挖而且没有挖透那么体积变小,表面积变大。
9.(2分)(2020秋 湖里区期中)图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分占空白部分面积的( )
A. B. C. D.
【考点】分数的意义和读写.
【专题】分数和百分数;数据分析观念.
【答案】A
【分析】设每个小长方形的长为a,宽为b,于是可以分别求出阴影部分和长方形的面积,进而求出阴影部分与空白部分面积的最简整数比。
【解答】解:假设每个小长方形的长为a,宽为b,
则长方形的面积是:a×4b=4ab;
阴影部分的面积是:(a×b÷2)×3=1.5ab;
空白部分的面积是:4ab﹣1.5ab=2.5ab;
所以阴影部分与空白部分面积的最简整数比是:
1.5ab:2.5ab=3:5;
答:阴影部分占空白部分面积的。
故选:A。
【点评】此题主要考查三角形和长方形的面积的计算方法的灵活应用。
二.填空题(共10小题,满分20分)
10.(4分)(2023秋 安丘市期中)填上合适的单位名称。
一支铅笔约重13 克 ;
一头牛约重240 千克 ;
鲸鱼体重34 吨 ,每小时游30 千米 。
【考点】根据情景选择合适的计量单位.
【专题】应用意识.
【答案】克;千克;吨;千米。
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:一支铅笔约重13克;
一头牛约重240千克;
鲸鱼体重34吨,每小时游30千米。
故答案为:克;千克;吨;千米。
【点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
11.(3分)(2022春 华安县期末)将算式改写成小数加法为 0.25 + 0.025 ,计算结果为 0.275 。
【考点】小数与分数的互化;小数的加法和减法.
【专题】运算能力.
【答案】0.25;0.025;0.275。
【分析】根据小数的意义,先把和化成小数后,再计算结果。
【解答】解:
=0.25+0.025
=0.275
答:将算式改写成小数加法为0.25+0.025,计算结果为0.275。
故答案为:0.25;0.025;0.275。
【点评】本题解题关键是理解小数的意义,熟练掌握小数加法的计算方法。
12.(1分)(2024 张家口)一个长为15分米、宽为0.6米、高为0.4米的长方体。最多可以切出 42 个棱长为2分米的小正方体。
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】42。
【分析】分别求出沿长、宽、高切,切出小正方体的个数,再相乘即可解答。
【解答】解:15÷2=7(个)……1(分米)
0.6米=6分米
6÷2=3(个)
0.4米=4分米
4÷2=2(个)
7×3×2
=21×2
=42(个)
答:最多可以切出42个棱长为2分米的小正方体。
故答案为:42。
【点评】此题考查长方体和正方体的体积。解答时注意单位要统一再计算。
13.(3分)(2023秋 辉县市校级月考) =0.3× =4× 0.25 =1。
【考点】倒数的认识.
【专题】分数和百分数;数据分析观念.
【答案】,,0.25。
【分析】若两个数的乘积是1,我们就称这两个数互为倒数。
【解答】解: 0.34×0.25=1
故答案为:,,0.25。
【点评】此题主要考查了倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数。
14.(2分)(2024秋 城厢区期中)“中国交通的发展日新月异。复兴号动车组的速度高达350千米/时,而磁悬浮列车的时速比复兴号快,堪比飞机,磁悬浮列车的速度是多少?”题目中将 复兴号动车组的速度 看作了单位“1”,根据题目中的信息写出的数量关系式是 磁悬浮列车的时速=复兴号动车组的速度×(1) 。
【考点】分数乘法应用题.
【专题】应用题;应用意识.
【答案】复兴号动车组的速度;磁悬浮列车的时速=复兴号动车组的速度×(1)。
【分析】依据题意可知,把复兴号动车组的速度看作单位“1”,磁悬浮列车的时速=复兴号动车组的速度×(1),由此解答本题即可。
【解答】解:把复兴号动车组的速度看作单位“1”,根据题目中的信息写出的数量关系式:磁悬浮列车的时速=复兴号动车组的速度×(1)。
故答案为:复兴号动车组的速度;磁悬浮列车的时速=复兴号动车组的速度×(1)。
【点评】解决本题的关键是找出题中数量关系。
15.(1分)(2024 电白区)我们曾经用如图所示方法解决了求三角形面积的问题,有这样的经验,我能算出图2的几何体体积是 6280 cm3。
【考点】圆柱的体积;长方体和正方体的体积.
【专题】应用题;应用意识.
【答案】6280。
【分析】找两个一模一样大的,几何体上下拼接在一起就会变成一个底面直径为20厘米,高为15+25=40(厘米)的圆柱体,圆柱体的体积是底面积乘高,而该几何体的体积则是圆柱体体积的一半,即可求出该几何体的体积。
【解答】解:如图
20÷2=10厘米
3.14×10×10×(25+15)
=3.14×100×40
=12560(立方厘米)
12560÷2=6280(立方厘米)
故答案为:6280。
【点评】解答此题首先先画图帮助理解题意,然后利用公式V=Sh解答。
16.(2分)如图,用相同的小正方体拼成了甲、乙两图形。甲的表面积 C 乙的表面积,甲的体积 A 乙的体积。
A.>
B.<
C.=
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【专题】几何直观.
【答案】C,A。
【分析】观察图形可知,甲的表面积等于24个小正方形的面积之和,乙的表面积也等于24个小正方形的面积之和,据此比较两个图形的表面积的大小;甲的体积等于8个小正方体的体积之和,乙的体积等于7个小正方体的体积之和,据此比较两个图形的体积的大小。
【解答】解:甲的表面积等于24个小正方形的面积之和,乙的表面积也等于24个小正方形的面积之和,所以两个图形的表面积相等;甲的体积等于8个小正方体的体积之和,乙的体积等于7个小正方体的体积之和,所以甲的体积大于乙的体积。
故答案为:C,A。
【点评】解答本题需熟练掌握表面积和体积的意义,准确识图是关键。
17.(2分)(2022春 惠来县期末)王林用做了一个。“学”的对面是 “教” ,“课”的对面是 “名” 。
【考点】正方体的展开图.
【专题】空间观念;几何直观.
【答案】“数”,“名”。
【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,“名”与“课”相对,“校”与“堂”相对,“数”与“学”相对。
【解答】解:王林用做了一个。“学”的对面是“数”,“课”的对面是“名”。
故答案为:“数”,“名”。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住规律,能快速解答此类题。
18.(1分)(2023秋 蚌山区校级期末)小华从图书馆借来一本《阿凡提的故事》,她第一天看了这本书的,第二天看的与第一天同样多,两天一共看了这本书的 。
【考点】分数加减法应用题.
【专题】应用题;应用意识.
【答案】。
【分析】第二天看的与第一天同样多,则第二天也看了这本书的。用()求出两天一共看了这本书的几分之几。
【解答】解:
答:两天一共看了这本书的。
故答案为:。
【点评】此题考查了运用分数加法解决实际问题。
19.(1分)(2022秋 天河区期末)在图中,再涂 3 块,涂色部分就占这个图形的。
【考点】分数的意义和读写.
【专题】分数和百分数;数据分析观念.
【答案】3。
【分析】将这个图形平均分成8块,其中1块占这个图形的,5块占这个图形的。题图中已经涂了2块,还需要涂(5﹣2)块。据此解答。
【解答】解:5﹣2=3(块)
则再涂3块,涂色部分就占这个图形的。
故答案为:3。
【点评】此题考查分数的认识。把一个整体平均分成若干份,用分数表示,分母是分成的份数,分子是要表示的份数。
三.计算题(共2小题,满分18分,每小题9分)
20.(9分)(2021春 盘龙区期末)用简便方法计算下面各题。
【考点】分数的加减混合运算.
【专题】运算能力.
【答案】1,2。
【分析】(1)运用加法交换律进行简算;
(2)运用加法交换律、结合律进行简算。
【解答】解:(1)
=1
=1
(2)
=()+()
=2
=2
【点评】此题考查了加法交换律、结合律的灵活运用。
21.(9分)(2023秋 汝州市校级月考)解下列方程。
3x﹣1.4=4.6
【考点】分数方程求解;小数方程求解.
【专题】简易方程;运算能力.
【答案】x=30;x=16;x=2。
【分析】(1)根据等式的性质,两边同时乘即可;
(2)首先根据等式的性质,两边同时减去1,然后两边同时乘即可;
(3)首先根据等式的性质,两边同时加上1.4,然后两边再同时除以3即可。
【解答】解:(1)
x25
x=30
(2)
1x﹣1=13﹣1
x=12
x12
x=16
(3)3x﹣1.4=4.6
3x﹣1.4+1.4=4.6+1.4
3x=6
3x÷3=6÷3
x=2
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
四.解答题(共5小题,满分20分)
22.(3分)(2021春 广元期末)一杯纯牛奶,聪聪喝了杯后,觉得有些凉,就兑满了热水,又喝了杯。他一共喝了多少杯纯牛奶?多少杯水?(用画图的方式解答)
【考点】异分母分数加减法.
【专题】数据分析观念;运算能力.
【答案】杯纯牛奶,杯水。
【分析】由题意可知:先喝的这是牛奶,还剩下(1)的牛奶,喝了杯后,觉得有些凉,就兑满了热水。说明加入了的水,这时水杯是满的,聪聪又喝了杯,那么聪聪第二次喝的牛奶就是剩下的(1)的,所以第二次喝的牛奶是(1)杯,两次一共喝的牛奶是杯加上(1)杯;求喝了多少杯水,杯子里的水一共有,第二次喝了杯,则喝的水就是杯的,由此即可解答。
【解答】解:作图如下:
牛奶:
(杯)
水:(杯)
答:他一共喝了杯纯牛奶,杯水。
【点评】此题考查的是分数乘法与分数加减法的混合运算。
23.(3分)(2023秋 房山区期末)画图表示的过程和结果。
【考点】分数乘分数.
【专题】运算能力.
【答案】;。
【分析】根据分数乘法的意义,先表示一个长方形的,再表示的,据此画图表示的过程和结果。
【解答】解:
【点评】本题解题的关键是熟练掌握分数乘法的计算方法。
24.(4分)(2022秋 闽清县期末)哪些形状是用4个拼成的?在括号里画“√”。
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】
【分析】根据图示,图一由3个小正方体拼成,图二和图三都是由4个小正方体拼成,据此解答即可。
【解答】解:解答如下:
【点评】本题考查了立体图形的拼组知识,结合题意分析解答即可。
25.(5分)(2023 南京)我们在小学阶段学过了正方体、长方体、圆柱体和圆锥体的体积,具体如下:
以后,当我研究“球的体积”时,我对这节课的学习目标可能有如下的想法:
(1)我会提出:“如何计算球的体积?”,还会提出: 如何求球的表面积 ?
(2)我会提出“怎样推导球的体积?”,我觉得可以用 转化 的方法。
(3)通过观察上面几何形体和体积计算公式,我发现:几何形体的体积都是3个变量的乘积。所以当球的半径为r时,我猜想,球的体积可能是 Vπr3 。
【考点】探索某些实物体积的测量方法.
【专题】综合填空题;几何直观.
【答案】(1)如何求球的表面积;(答案不唯一)
(2)转化;
(3)Vπr3。
【分析】(1)还会提出:如何求球的表面积?(答案不唯一)
(2)把球放入内直径和高与球直径相等的圆柱形容器里,加满水,分别记录取出球前后,容器内水的高度,由此计算球的体积;(答案不唯一)
(3)依据题意推算球的体积。(答案不唯一)
【解答】解:由分析可知,(1)还会提出:如何求球的表面积?(答案不唯一)
(2)可以用转化的方法。
(3)球的体积可能是Vπr3
故答案为:(1)如何求球的表面积;(答案不唯一)(2)转化;(3)Vπr3。
【点评】本题考查的是探索某些实物体积的测量方法的应用。
26.(5分)(2021秋 互助县期末)如图,有6个△,把其中涂黑色。
【考点】分数乘法应用题.
【专题】应用意识.
【答案】。
【分析】一共有6个△,把三角形的总数看成单位“1”,用6乘即可求出需要涂黑色的个数。
【解答】解:64(个)
答:需要涂黑4个三角形。
【点评】本题的关键是找出单位“1”,已知单位“1”的量求它的几分之几是多少用乘法求解。
五.应用题(共4小题,满分24分)
27.(5分)(2024春 天河区期末)某森林公园的林木面积是公顷。这个森林公园的草地面积和林木面积一共是多少公顷?
【考点】分数加减法应用题.
【专题】应用题;应用意识.
【答案】公顷。
【分析】已知林木面积是公顷,用林木面积减去就是草地面积,然后把林木面积和草地面积相加即可解答此题。
【解答】解:
(公顷)
答:这个森林公园的草地面积和林木面积一共是公顷。
【点评】解答此题的关键是要先求出草地的面积,然后把林木面积和草地面积相加即可。
28.(5分)(2023秋 临漳县期中)青藏铁路是世界上海拔最高、线路最长的高原铁路,西宁至拉萨的铁路全长1956千米。一列火车从西宁开出,已经行了全程的,距离拉萨还有多少千米?
【考点】分数乘法应用题.
【专题】应用题;应用意识.
【答案】326千米。
【分析】距离拉萨的距离=铁路全长×(1),由此列式计算即可。
【解答】解:1956×(1)
=1956
=326(千米)
答:距离拉萨还有326千米。
【点评】解决本题的关键是找出题中的数量关系。
29.(5分)(2023春 蠡县期末)一个封闭的长方体玻璃容器(玻璃厚度不计)长4分米,宽3分米,高8分米,里面水深5分米(如图①)。现在以这个容器的右侧为底,侧放在桌面上(如图②)。这时水深多少分米?
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】2.5分米。
【分析】根据长方体体积公式V=abh,计算出图1中水的体积,也就是图2中水的体积;根据长方体体积公式可得h=V÷a÷b,据此计算出图2的水深。
【解答】解:4×3×5÷8÷3
=12×5÷8÷3
=60÷8÷3
=7.5÷3
=2.5(分米)
答:这时水深2.5分米。
【点评】本题主要考查长方体体积计算公式的应用,熟练掌握长方体体积公式是解答本题的关键。
30.(9分)(2023春 永嘉县期末)先从一张长40厘米,宽35厘米的长方形铁皮的四个角各剪去一个边长是5厘米的正方形,然后做成一个无盖的长方体盒子。
(1)这个盒子用了多少平方厘米铁皮?
(2)这个铁皮盒子的容积是多少立方厘米?
【考点】长方体、正方体表面积与体积计算的应用.
【专题】运算能力.
【答案】(1)1300平方厘米;(2)3750立方厘米。
【分析】(1)观察图形可知,折成的长方体的长为40﹣5×2=30(厘米),宽为35﹣5×2=25(厘米),高是5厘米,铁皮的面积就是长方体的五个面的面积,长方体的五个面的面积=长×宽+(长×高+宽×高)×2,据此计算即可;
(2)根据长方体的容积公式:V=abh,据此代入数值进行计算即可。
【解答】解:(1)40﹣5×2
=40﹣10
=30(厘米)
35﹣5×2
=35﹣10
=25(厘米)
30×25+(30×5+25×5)×2
=750+(150+125)×2
=750+275×2
=750+550
=1300(平方厘米)
答:这个盒子用了1300平方厘米铁皮。
(2)30×25×5
=750×5
=3750(立方厘米)
答:这个铁皮盒子的容积是3750立方厘米。
【点评】本题考查长方体的表面积和容积,熟记公式是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
