苏科版八年级数学下册 9.4.1矩形 复习题(含解析)
文档属性
| 名称 | 苏科版八年级数学下册 9.4.1矩形 复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 00:00:00 | ||
图片预览



文档简介
9.4.1矩形复习题
【类型一:矩形的性质】
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=12cm,则AB的长为 cm.
2.如图,在矩形ABCD中,点E是CD的中点,点F在BD上,BF=3DF,若AB=4,BC=3,则EF的长为( )
A.1 B. C. D.
3.如图,P是矩形ABCD的对角线BD上一点,AB=3,BC=5,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF,则AP+EF的最小值为( )
A. B.4 C. D.8
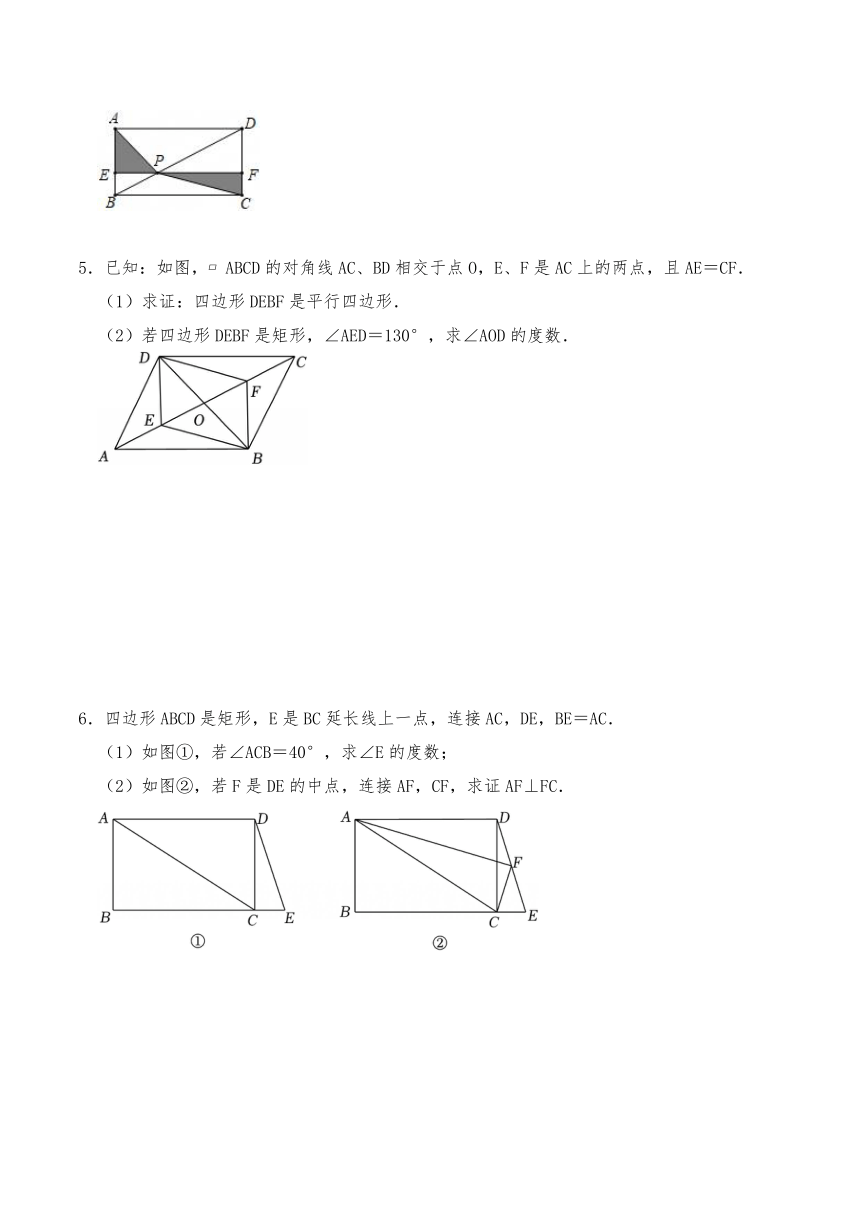
4如图,点P是矩形ABCD的对角线BD上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PA,PC.若BE=2,PF=6,则图中阴影部分的面积为 .
5.已知:如图, ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且AE=CF.
(1)求证:四边形DEBF是平行四边形.
(2)若四边形DEBF是矩形,∠AED=130°,求∠AOD的度数.
6.四边形ABCD是矩形,E是BC延长线上一点,连接AC,DE,BE=AC.
(1)如图①,若∠ACB=40°,求∠E的度数;
(2)如图②,若F是DE的中点,连接AF,CF,求证AF⊥FC.
【类型二:矩形的判定】
7.如图,四边形ABCD的对角线AC,BD交于点O.根据图中所标示的数据,再添加下列一个条件,其中能使四边形ABCD为矩形的条件有①OB=5;②OD=5;③∠ADC=90°.( )
A.0个 B.1个 C.2个 D.3个
8.如图,诚诚用橡胶皮和布料自制了一块四边形鼠标垫,为了检验这块鼠标垫是不是标准的矩形,他想出了以下几种方案,其中合理的是( )
A.测量一组对边是否平行且相等
B.测量两组对边是否分别相等
C.测量其中的三个角是否都为直角
D.测量对角线是否相等
9.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F在对角线BD上,且BE=DF,连接AE,AF,CE,CF.
(1)求证:△AOE≌△COF.
(2)当OA=OE时,求证四边形AECF是矩形.
10.如图,在 ABCD中,O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC,若AB=2,,求OC的长.
【类型三:矩形的翻折问题】
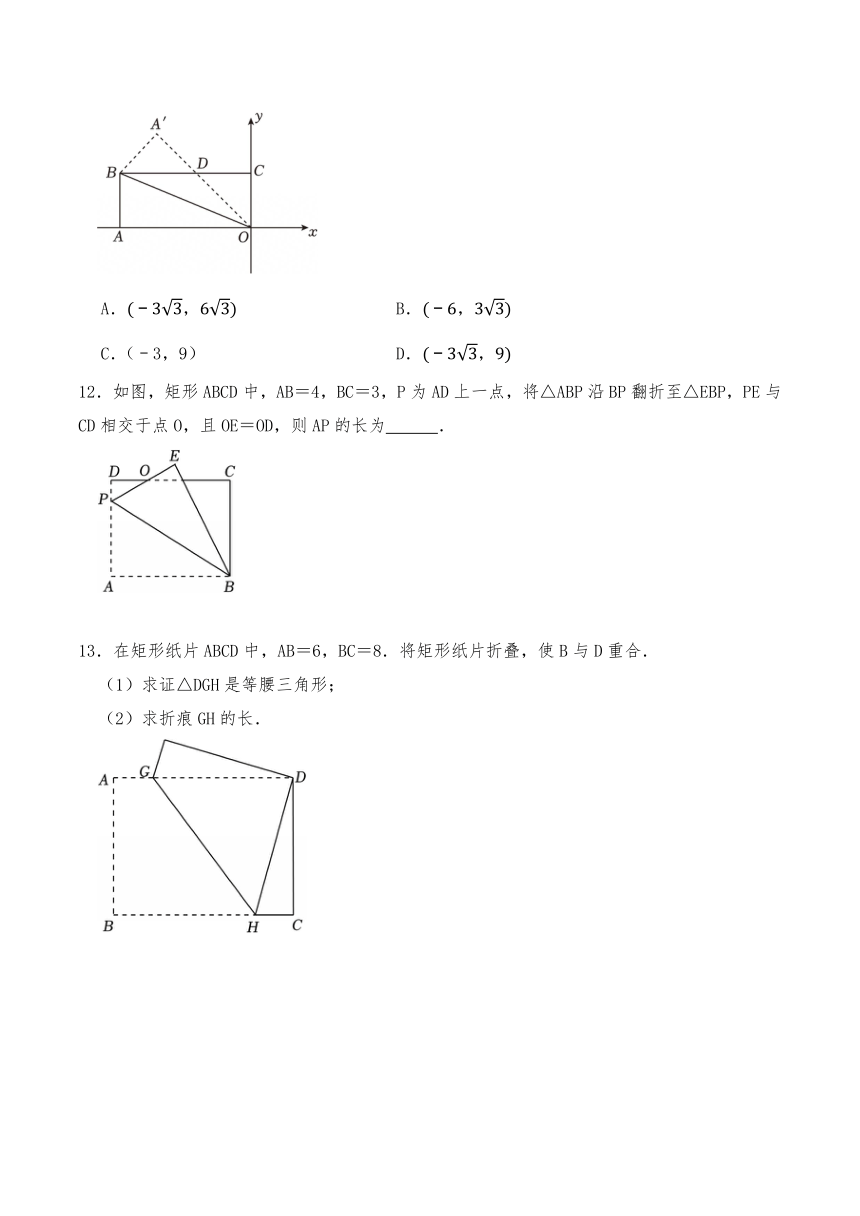
11.如图,矩形ABCO如图放置在平面直角坐标系中,其中AB=6,∠AOB=30°,若将其沿着OB对折后,A′为点A的对应点,则A′的坐标为( )
A. B.
C.(﹣3,9) D.
12.如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 .
13.在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片折叠,使B与D重合.
(1)求证△DGH是等腰三角形;
(2)求折痕GH的长.
14.如图1,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)若∠BAM=32°,则∠ANM= °;
(2)如图2,连接CN.求证:四边形AMCN为菱形;
(3)若△AMN的面积与△ABM的面积比为3:1,BM=1,求MN的长.
【类型四:矩形的旋转问题】
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=114°,则α= °.
16.如图1,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,连接DF、DG.
(1)如图2,点E落在对角线BD上,AD与EF相交于点H,
①连接AF,求证:四边形ABDF是平行四边形;
②求线段AH的长度;
(2)在矩形AEFG绕点A旋转一周的过程中,△DFG面积的最大值为 .
【类型五:矩形的动点问题】
17.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.22 D.26
18.如图,在平行四边形ABCD中,对角线BD=10cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)证明:当E在AO上运动,F在CO上运动,且E与F不重合时,四边形DEBF是平行四边形:
(2)点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.
19.如图①,在矩形ABCD中,AB=3,AD=5,点E在边BC上且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动,作∠PEQ=90°,EQ交边AD或DC于点Q,连接PQ,当Q与点C重合时点P停止运动,设点P的运动时间为t秒(t>0).
(1)当点P与点B重合时,线段PQ的长为 ;
(2)当点Q与点D重合时,求AP的长;
(3)如图②,当点P在AD上运动时,证明△PEQ始终是等腰直角三角形;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分图形为轴对称四边形时,直接写出t的取值范围.
【类型六:与矩形有关的作图题】
20.如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
21.如图,Rt△ABC中,∠ABC=90°.
(1)尺规作图:作矩形ABCD;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若AB=4,BC=8,点E为边AD上一点,若BE的中垂线分别交边AD、边BC于点M、N,则MN的长的取值范围为 .(如需画草图,请使用试题卷中的图2)
22.规定:每个顶点都在格点的四边形叫做格点四边形.在10×6的正方形网格中画出符合要求的格点四边形(设每个小正方形的边长为1).
(1)在图甲中画出一个以AB为边的平行四边形,且它的面积为8.
(2)在图乙中画出一个以AB为对角线的矩形,且它的面积为6.
【类型七:矩形综合题】
23.如图,取一张矩形的纸进行折叠,具体操作过程如下:
(1)【探究发现】:
操作一:先把矩形ABCD对折,折痕为EF;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中∠ABP= °;
(2)【类比应用】:小明将矩形纸片换成边长为4cm的正方形纸片,继续探究,过程如下:将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ= °,CQ= ;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)【拓展延伸】:在(2)的探究中,当QF=1cm,请直接写出AP的长.
24.如图,在矩形ABCD中,AB=8,BC=6,点E是边AB上一点且BE=2,点P是线段AE上一动点(不与端点A重合,可以与端点E重合),将△APD沿PD折叠,得到点A的对称点为点F,连接BF.
(1)若点P在边AB中点时,则BF的长为 ;
(2)若△BPF为直角三角形时,求BF的长;
(3)将△APD绕点D逆时针旋转90°得到△DMN,点A的对应点为点M,点P的对应点为点N,连接FN.若△DFN为等腰三角形时,求BF的长.
25.折纸不仅是一项有趣的活动,也是一项益智的数学活动.今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论.
实践操作,解决问题
如图1,将矩形纸片ABCD沿对角线AC翻折,使点D′落在矩形ABCD所在平面内,边BC和AD′相交于点E,连接BD′.发现:结论①AE=EC;结论②BD′∥AC.
(1)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
(2)东京沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形(如图3所示).沿对称轴EF再次折叠后,得到的仍是轴对称图形,则京京折叠的矩形纸片的长宽之比为 ;
(3)新题探究:如图4所示,平行四边形ABCD中,∠ABC=60°,AB=2(AB≠BC).将△ADC沿对角线AC翻折.使点D′落在ABCD所在平面内,连接BD′,当△BCD′恰好为直角三角形时,BC的长度为 .
参考答案
【类型一:矩形的性质】
1.
【分析】根据相等垂直平分线的性质得到AB=AO,再由矩形的性质得到AO=6cm,则AB=AO=6cm.
【解答】解:∵AE垂直且平分线段BO,
∴AB=AO,
∵四边形ABCD是矩形,对角线AC与BD相交于点O,BD=12cm,
∴,
∴AB=AO=6cm,
故答案为:6.
2.
【分析】根据矩形的性质得到∠C=90°,CD=AB=4,BC=3,根据勾股定理得到BD5,得到DFBD,过F作FH⊥CD于H,根据相似三角形的性质即可得到结论.
【解答】解:在矩形ABCD中,∵∠C=90°,CD=AB=4,BC=3,
∴BD5,
∵BF=3DF,
∴DFBD,
过F作FH⊥CD于H,
∴FH∥BC,
∴△DFH∽△DBC,
∴,
∴,
∴FH,DH=1,
∵点E是CD的中点,
∴DE,
∴EH=DH=1,
∴EF=DF,
故选:B.
3.
【分析】连接CP,根据矩形的性质得到EF=CP,AP+EF的最小值即为AP+CP的最小值,当A,P,C三点共线时,AP+CP的值最小,且为AC的长度,根据勾股定理得到AC,于是得到结论.
【解答】解:连接CP,
∵四边形ABCD是矩形,
∴EF=CP,
∴AP+EF的最小值即为AP+CP的最小值,
当A,P,C三点共线时,AP+CP的值最小,且为AC的长度,
∵四边形ABCD是矩形,
∴AC,
∴AP+EF的最小值为,
故选:C.
4.
【分析】由矩形的性质可证明S△PEA=S△PFC,即可求解.
【解答】解:作PM⊥AD于M,交BC于N.如图2:
则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴CF=BE=2,
∴S△AEP=S△AMP,S△CFP=S△CNP,
∴S△AEP=S△CFPPF×CF6×2=6,
∴图中阴影部分的面积S阴=6+6=12.
故答案为:12.
5.(1)证明:在 ABCD中,OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形;
(2)解:∵四边形DEBF是矩形,
∴OE=OD,
∴∠ODE=∠OED,
∵∠AED+∠OED=180°,
∴∠OED=180°﹣∠AED=50°,
∴∠AOD=180°﹣∠ODE﹣∠OED=80°.
6.(1)解:如图①,连接BD,与AC交于点O,
∵四边形ABCD是矩形,
∴AC=BD,OBBD,OCAC,
∴OB=OC,
∴∠DBC=∠ACB=40°,
∵BE=AC,
∴BD=BE,
∴∠BDE=∠E,
∴∠E70°;
(2)证明:如图②,延长CF交AD延长线于点G,
∵AG∥BE,
∴∠GDF=∠E,∠G=∠ECF,
∵F是DE的中点,
∴DF=EF,
∴△DFG≌△EFC(AAS),
∴DG=EC,GF=CF.
∴BC+CE=AD+DG,即AG=BE,
∵BE=AC,
∴AG=AC,
又∵GF=CF,
∴AF⊥FC.
【类型二:矩形的判定】
7.
【分析】添加OD=5或∠ADC=90°,根据对角线互相平分且相等的四边形是矩形即可判断.
【解答】解:∵∠ABC=90°,AO=CO=5,
∴,AC=10,
①添加OD=5,
则BO=DO,BD=10,
∴四边形ABCD为平行四边形,
又AC=BD=10,
∴平行四边形ABCD为矩形;
②添加∠ADC=90°,
则,
∴BO=DO,BD=10,
∴四边形ABCD为平行四边形,
又AC=BD=10,
∴平行四边形ABCD为矩形;
添加OB=5,无法得到对角线互相平分,无法推出平行四边形ABCD为矩形;
故选:C.
8.
【分析】根据矩形的判定方法,逐一进行判断即可.
【解答】解:A、测量一组对边是否平行且相等,只能判断出这块鼠标垫是不是标准的平行四边形,故A选项不符合题意;
B、测量两组对边是否分别相等,只能判断出这块鼠标垫是不是标准的平行四边形,故B选项不符合题意;
C、测量其中的三个角是否都为直角,可以检验这块鼠标垫是不是标准的矩形,故C选项符合题意;
D、测量对角线是否相等,不能检验这块鼠标垫是不是标准的矩形,故D选项不符合题意;
故选:C.
9.(1)证明:∵ ABCD,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DE,即OE=OF,
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS).
(2)解:由(1)可得△AOE≌△COF.
∴OA=OC,OE=OF,
∴四边形AECF为平行四边形,
∵OA=OE,
∴OA=OE=OC=OF,
∴AC=EF,
∴四边形AECF是矩形.
10.(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=2,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=1,
∴OF为△BDE的中位线,
∴,
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∴CF=CD+DF=3,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
【类型三:矩形的翻折问题】
11.
【分析】作AD⊥x轴,根据含 30°角直角三形的性质,及勾 股定理,求出AO,根据折叠的性质,求出AO,∠AOD,在Rt△ADO中,求出DO,AD,根据 第二象限内点的特征,即可求解,
【解答】解:过点A作AD⊥x轴,交x轴于点D,
在Rt△BAO 中,AB=6,∠AOB=30°,
∴BO=2AB=2×6=12,,
由折叠的性质可得:,
∠A'OB=∠AOB=30°,
即:∠AOD=2∠AOB=2×30°=60°,
在Rt△ADO 中,,,
∵点A在第二象限,,
故选:D.
12.
【分析】由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=4,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=3﹣x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
【解答】解:如图所示:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=3,CD=AB=4,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=4,
在△ODP和△OEG中,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=3﹣x,DG=x,
∴CG=4﹣x,BG=4﹣(3﹣x)=1+x,
根据勾股定理得:BC2+CG2=BG2,
即32+(4﹣x)2=(x+1)2,
解得:x=2.4,
∴AP=2.4;
故答案为:2.4.
13.(1)证明:如图,矩形纸片折叠后,设A与F重合,过点G作GE⊥BC于点E,
由折叠的性质得:DH=BH,FD=BA,FG=AG,∠GHB=∠GHD,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AB=CD,AD=BC,AD∥BC,
∴∠DGH=∠GHB,
∴∠DGH=∠GHD,
∴GD=HD,
∴△DGH是等腰三角形.
(2)解:∵GD=HD,
∴GD=DH=BH,
∵AB=6,BC=8,
∴DF=CD=6,AD=8,
设BH=x,则HC=8﹣x,由勾股定理得:x2=(8﹣x)2+62,
解得:,
∴,
∴,
∴,
在Rt△GEH中,由勾股定理得:,
∴.
14.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∵∠BAM=32°,
∴∠AMB=90°﹣∠BAM=58°,
∵折叠,
∴∠AMN=∠NMC61°,
∵AD∥BC,
∴∠ANM=∠CMN=61°,
故答案为:61;
(2)证明:∵折叠,
∴CM=AM,AE=CD,∠AMN=∠CMN,∠E=∠D=90°,
∴△CDN≌△AEN(SAS),
∴AN=CN,
∵ABCD是矩形,
∴AD∥BC,
∴∠AMN=∠ANM,
∴∠ANM=∠AMN,
∴AM=AN,
∴AM=CM=AN=CN,
∴四边形AMCN为菱形;
(3)解:作MF⊥AN于点F,
∵AD∥BC,
∴△AMN和△ABM是等高的两个三角形
∴S△AMN:S△ABM=3:1=AN:BM,
∵BM=1,
∴AN=3,
∵AM=AN,
∴AM=3,
∵MF⊥AN,∠B=∠DAB=90°,
∴ABMF是矩形,
∴BM=AF=1,
∴根据勾股定理FM2,NF=2,
在Rt△MNF中,MN2.
【类型四:矩形的旋转问题】
15.
【分析】先利用旋转的性质得到∠ADC=∠D=90°,∠DAD′=α,再利用四边形内角和计算出∠BAD=66°,然后利用互余计算出∠DAD′,从而得到α的值.
【解答】解:∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
∴∠ADC=∠D'=90°,∠DAD′=α,
∵∠ABC=90°,
∴∠BAD'=180°﹣∠2,
又∵∠2=∠1=114°,
∴∠BAD'=180°﹣114°=66°,
∴∠DAD′=∠BAD﹣∠BAD'=90°﹣66°=24°,
即α=24°.
故答案为:24.
16.(1)①证明:如图,
∵四边形形ABCD是矩形,
∴AD=BC,∠BAD=∠ABC=90°,
∵旋转,
∴AE=AB,EF=BC=AD,∠1=∠ABC=∠BAD=90°,
在△ABD和△EAF中,
,
∴△ABD≌△EAF(SAS),
∴∠2=∠EAF,BD=AF,
∵AB=AE,
∴∠3=∠2=∠EAF,
∴AF∥BD,
又∵AF=BD,
∴四边形ABDF是平行四边形;
②解:设HD=x,则AH=4﹣x,
∵四边形ABDF是平行四边形,
∴AB∥DF,AB=DF,
∴∠ADF=∠BAD=90°,
又∵∠1=90°,
∴∠ADF=∠1,
∵AE=AB,AB=DF,
∴AE=DF,
在△AEH和△FDH中,
,
∴△AEH≌△FDH(SAS),
∴HE=HD=x,
∵∠1=90°,
∴EA2+EH2=AH2,
又∵AH=4﹣x,EA=AB=3,EH=x,
∴32+x2=(4﹣x)2,
∴x,
∴AH=4﹣x.
(2)解:∵将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,
∴旋转过程中,GF是定值,
当D,A,G三点共时,三角形DFG的面积最大,如图,
此时DG=8,
∴S△DFG12,
故答案为:12.
【类型五:矩形的动点问题】
17.
【分析】根据函数的图象、结合图形求出AB、BC的值,即可得出矩形ABCD的周长.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=4,x=9时,接着变化,说明CD=9﹣4=5,
∴AB=5,BC=4,
∴矩形ABCD的周长=2(AB+BC)=18.
故选:A.
18.解:(1)∵E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形能为矩形.理由如下:
分为两种情况:
①∵四边形DEBF是矩形,
∴BD=EF=10cm,
即AE=CF=0.5t cm,
则16﹣0.5t﹣0.5t=10,
解得:t=6;
②当E到F位置上,F到E位置上时,AE=CF=0.5t cm,
则0.5t﹣10+0.5t=16,
解得:t=26,
即当运动时间t=6s或28s时,以D、E、B、F为顶点的四边形是矩形.
19.解:(1)如图所示,连接BQ,
∵四边形ABCD是矩形,
∴∠BAQ=∠ABE=90°,∠PEQ=90°,
∴四边形ABEQ是矩形,
当点P和点B重合时,
QE=AB=3,BE=2,
在Rt△QBE中,
BQ,
故答案为:;
(2)如图,
设AP=x,则BP=3﹣x,
在Rt△APQ中,AP2+AQ2=PQ2,
∴PQ2=52+x2,
在Rt△PBE中,PB2+BE2=PE2,
∴PE2=(3﹣x)2+22,
在Rt△ECQ中,EC2+CQ2=EQ2,
∴PQ2=32+32,
∵∠PEQ=90°,
∴PE2+EQ2=PQ2,
∴22+(3﹣x)2+32+32=52+x2,
故x=1,
即AP长为1;
(3)证明:如图2,过点P作PH⊥BC于点H,
则PH=3,
同理可得∠EPH=∠QEC,
∵EC=BC﹣BE=3,
∴PH=EC,
又∠PHE=∠C=90°,
∴△PHE≌△ECQ(ASA),
∴PE=HE,
∴△PQE是等腰直角三角形;
(4)①如图所示,当点P在BE上时,
∵QE=QF=3,AQ=BE=2,
在Rt△AQF中,
AF,
则BF=3,
∵PE=t,
∴BP=2﹣t,PF=PE=t,
在Rt△PBF中,PF2=PB2+FB2,
∴t2=(3)2+(2﹣t)2,
解得:t,
t时,点F在矩形内部,
∴0<t,符合题意,
②当P点在AB上时,当F,A重合时符合题意,此时如图,
则PB=t﹣BE=t﹣2,PE=AP=AB﹣PB=3﹣(t﹣2)=5﹣t,
在Rt△PBE中,PE2=PB2+BE2,
∴(5﹣t)2=(t﹣2)2+22,
解得t,
③当点P在AD上,当F,D重合时,此时点Q与点C重合,
则PFQE是正方形,此时t=2+3+2=7,
∴0<t或t或t=7.
【类型六:与矩形有关的作图题】
20.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
21.解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,当点M与A重合时,MN的长最大,最大值AB=4;
如图2中,当点E以D重合时,连接BM,设BD,AC交于点O,MN的长最小,设BM=DM=x,则有x2=42+(8﹣x)2,
解得x=5,
∵∠BAD=90°,AB=4,AD=8,
∴BD4,
∴OB=OD=2,
∴OM=ON,
∴MN=2,
∴2MN≤4.
故答案为:2MN≤4.
22.解:(1)如图甲所示,平行四边形ABCD即为所求(答案不唯一).
(2)如图乙所示,矩形AEBF即为所求(答案不唯一).
【类型七:矩形综合题】
23.解:(1)∵,
∴,
∴∠BEM=90°,
如图1,取BM的中点O,连接EO,
∴,
∴△BEO为等边三角形,
∴∠BME=30°,
∴∠ABM=60°,
∴∠ABP=∠PBM=30°,
故答案为:30;
(2)①四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠C=90°,
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°,
∴BM=BC,
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴MBQ=∠CBQ,QM=QC,
同法(1)可得:∠MBC=30°,
∴∠MBQ=∠CBQ=15°,
∴∠ABM=90°﹣30°=60°,
∴∠APM=180°﹣60°=120°,
∴∠QPD=180°﹣120°=60°,
在Rt△ABP中,BP=2AP,
根据勾股定理:BP2﹣AP2=AB2,
即3AP2=16,
解得:,
∴,
在Rt△PDQ中,PQ=2PD,
根据勾股定理:DQ2=PQ2﹣PD2,即DQ2=3PD2,
∴,
∴,
故答案为:15,;
②∠MBQ=∠CBQ,理由如下:
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ;
(3)当点Q在点F的下方时,如图3.1,
∵FQ=lcm,DF=FC=2cm,AB=4cm,
∴QC=CD﹣DF﹣FQ=4﹣2﹣1=l(cm),DQ=DF+FQ=2+1=3(cm),
由(2)可知,QM=QC,
设AP=PM=x,PD=4﹣x,
∴PD2+DQ2=PQ2,
即(4﹣x)2+32=(x+1)2,
解得:,
∴;
当点Q在点F的上方时,如图3.2,
∵FQ=lcm,DF=FC=2cm,AB=4cm,
∴QC=3cm,DQ=lcm,
由(2)可知,QM=QC,
设AP=PM=x,PD=4﹣x,
∴PD2+DQ2=PQ2,
即(4﹣x)2+12=(x+3)2,
解得:,
∴.
综上所述,或.
24.解:(1)连接AF交DP于点M,
∵将△APD沿PD折叠,得到点A的对称点为点F,
∴DP垂直平分AF,
∵P是AB的中点,
∴PM是△ABF的中位线,
∴BF=2PM,
∵AD=6,APAB=4,
∴DP2,
∵,
∴AM,
∴PM,
∴BF.
故答案为:;
(2)若△BPF为直角三角形.
①当∠PBF=90°时,不存在.
②当∠PFB=90°时(如图4),
∵将△APD 沿PD折叠,得到点A的对称点为点F.
∴∠DFP=∠B=90°,
∴∠DFP+∠PFB=180°,
∴点D,F,B共线.即点F在矩形对角线DB上.
∵AD=6,AB=8,∠A=90°,
∴BD10.
∵DF=DA=6,
∴BF=10﹣6=4.
此时AP=PF=3.
③当∠BPF=90°时(如图 5),
∵∠A=90°,∠DFP=90°,
∴四边形ADFP是矩形.
∴点F在DC边上,
∵BE=2,EF=6,∠BEF=90°,
∴,
∴BF的长为4或;
(3)若△DFN为等腰三角形.
①当DF=DN时,不存在.
②当 FD=FN时(如图6),
设∠ADP=x,
∵将△APD 沿PD折叠,得到点A的对称点为点F.
∴∠ADP=∠PDF=x,
∵将△APD 绕点D逆时针旋转90°得到△DMN.
∴∠PDN=90°,
∴∠FDN=∠FND=∠DPA=90°﹣x,
∴∠FND=∠MND=90°﹣x,
即∠FND与∠MND重合.
∴点F与点M重合,
∴.
③当ND=NF时(如图7),
过点N作NH⊥DF垂足为H.
∵∠ADP=∠PDF=∠MDN,
∴∠ADP=∠DNH,
∵∠A=∠DHN=90°,DN=DP,
∴△NDH≌△DPA(AAS),
∴,
由(2)可知,当AP=3 时,BF=4.
∴BF的长为4或.
25.解:(1)AE=EC,BD′∥AC,理由如下,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠EAC,
∵折叠,
∴AD=AD′,∠DAC=∠D′AC,
∴∠EAC=∠ECA,
∴AE=EC,
∵折叠,
∴AD=AD′,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD′=BC,
∵EC=EA,
∴AD′﹣AE=BC﹣CE,即BE=ED′,
∴,
又∵,∠AEC=∠BED′,
∴∠EAC=∠ED′B,
∴BD′∥AC;
(2)当点D′与B点不重合时,如图,
依题意,EF=ED′=BE,AE=EC,∠EFC=∠AFE=90°,
设∠ACB=α,则∠EAF=∠ACB=∠BAE,
∵∠ACB+∠BAC=90°,
∴α+2α=90°,
解得:α=30°,
∴,
在Rt△ABC中,,
∴矩形纸片的长宽之比为,
当点D′与B点重合时,如图,
此时ABCD是正方形,
∴矩形纸片的长宽之比为1:1,
综上矩形纸片的长宽之比1:1或;
(3)当∠CBD′=90°时,如图,设CD′与AB交于点E,
由(1)可得BD′∥AC,
∴∠ACB=180°﹣∠CBD′=90°,
在Rt△ABC中,∵∠ABC=60°,AB=2,
∴∠BAC=30°,
∴;
如图,当∠CD′B=90°时,由(1)可得BD′∥AC,
∴∠ACD′=180°﹣∠BD′C=90°,
∵折叠,
∴∠ACD=∠ACD′=90°,
∴D,C,D′三点共线,
∵四边形ABCD是平行四边形,∠ABC=60°,AB=2,
∴∠D=60°,CD=AB=2,
∴∠DAC=30°,
在Rt△ACD中,A D=2 C D=4,
∴BC=AD=4;
如图,当∠BCD′=90°时,
∵∠ABC=60°,
∴∠BEC=30°,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DCA=∠EAC,
∵折叠,
∴AD=AD′,∠DCA=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC,
设BC=m,
∴BE=2m,,
∴,
∴,
∴;
如图,当∠BCD′=90°时,同理可得∠CDE=∠D=∠ABC=60°,∠CED=30°=∠AEB,CD=CD′=2=AB,
∴D′E=4,,
同理可得:AE=CE,AD′=AD=BC,
∴BE=D′E=4,
∴;
综上所述:BC的长度为1或4或或.
【类型一:矩形的性质】
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=12cm,则AB的长为 cm.
2.如图,在矩形ABCD中,点E是CD的中点,点F在BD上,BF=3DF,若AB=4,BC=3,则EF的长为( )
A.1 B. C. D.
3.如图,P是矩形ABCD的对角线BD上一点,AB=3,BC=5,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF,则AP+EF的最小值为( )
A. B.4 C. D.8
4如图,点P是矩形ABCD的对角线BD上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PA,PC.若BE=2,PF=6,则图中阴影部分的面积为 .
5.已知:如图, ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,且AE=CF.
(1)求证:四边形DEBF是平行四边形.
(2)若四边形DEBF是矩形,∠AED=130°,求∠AOD的度数.
6.四边形ABCD是矩形,E是BC延长线上一点,连接AC,DE,BE=AC.
(1)如图①,若∠ACB=40°,求∠E的度数;
(2)如图②,若F是DE的中点,连接AF,CF,求证AF⊥FC.
【类型二:矩形的判定】
7.如图,四边形ABCD的对角线AC,BD交于点O.根据图中所标示的数据,再添加下列一个条件,其中能使四边形ABCD为矩形的条件有①OB=5;②OD=5;③∠ADC=90°.( )
A.0个 B.1个 C.2个 D.3个
8.如图,诚诚用橡胶皮和布料自制了一块四边形鼠标垫,为了检验这块鼠标垫是不是标准的矩形,他想出了以下几种方案,其中合理的是( )
A.测量一组对边是否平行且相等
B.测量两组对边是否分别相等
C.测量其中的三个角是否都为直角
D.测量对角线是否相等
9.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F在对角线BD上,且BE=DF,连接AE,AF,CE,CF.
(1)求证:△AOE≌△COF.
(2)当OA=OE时,求证四边形AECF是矩形.
10.如图,在 ABCD中,O为线段AD的中点,延长BO交CD的延长线于点E,连接AE,BD,∠BDC=90°.
(1)求证:四边形ABDE是矩形;
(2)连接OC,若AB=2,,求OC的长.
【类型三:矩形的翻折问题】
11.如图,矩形ABCO如图放置在平面直角坐标系中,其中AB=6,∠AOB=30°,若将其沿着OB对折后,A′为点A的对应点,则A′的坐标为( )
A. B.
C.(﹣3,9) D.
12.如图,矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 .
13.在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片折叠,使B与D重合.
(1)求证△DGH是等腰三角形;
(2)求折痕GH的长.
14.如图1,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)若∠BAM=32°,则∠ANM= °;
(2)如图2,连接CN.求证:四边形AMCN为菱形;
(3)若△AMN的面积与△ABM的面积比为3:1,BM=1,求MN的长.
【类型四:矩形的旋转问题】
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为α(0°<α<90°),若∠1=114°,则α= °.
16.如图1,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,连接DF、DG.
(1)如图2,点E落在对角线BD上,AD与EF相交于点H,
①连接AF,求证:四边形ABDF是平行四边形;
②求线段AH的长度;
(2)在矩形AEFG绕点A旋转一周的过程中,△DFG面积的最大值为 .
【类型五:矩形的动点问题】
17.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则矩形ABCD的周长是( )
A.18 B.20 C.22 D.26
18.如图,在平行四边形ABCD中,对角线BD=10cm,AC=16cm,AC,BD相交于点O,若E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s.
(1)证明:当E在AO上运动,F在CO上运动,且E与F不重合时,四边形DEBF是平行四边形:
(2)点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形是否可能为矩形?如能,求出此时的运动时间t的值;如不能,请说明理由.
19.如图①,在矩形ABCD中,AB=3,AD=5,点E在边BC上且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动,作∠PEQ=90°,EQ交边AD或DC于点Q,连接PQ,当Q与点C重合时点P停止运动,设点P的运动时间为t秒(t>0).
(1)当点P与点B重合时,线段PQ的长为 ;
(2)当点Q与点D重合时,求AP的长;
(3)如图②,当点P在AD上运动时,证明△PEQ始终是等腰直角三角形;
(4)作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分图形为轴对称四边形时,直接写出t的取值范围.
【类型六:与矩形有关的作图题】
20.如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
21.如图,Rt△ABC中,∠ABC=90°.
(1)尺规作图:作矩形ABCD;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若AB=4,BC=8,点E为边AD上一点,若BE的中垂线分别交边AD、边BC于点M、N,则MN的长的取值范围为 .(如需画草图,请使用试题卷中的图2)
22.规定:每个顶点都在格点的四边形叫做格点四边形.在10×6的正方形网格中画出符合要求的格点四边形(设每个小正方形的边长为1).
(1)在图甲中画出一个以AB为边的平行四边形,且它的面积为8.
(2)在图乙中画出一个以AB为对角线的矩形,且它的面积为6.
【类型七:矩形综合题】
23.如图,取一张矩形的纸进行折叠,具体操作过程如下:
(1)【探究发现】:
操作一:先把矩形ABCD对折,折痕为EF;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中∠ABP= °;
(2)【类比应用】:小明将矩形纸片换成边长为4cm的正方形纸片,继续探究,过程如下:将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ= °,CQ= ;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)【拓展延伸】:在(2)的探究中,当QF=1cm,请直接写出AP的长.
24.如图,在矩形ABCD中,AB=8,BC=6,点E是边AB上一点且BE=2,点P是线段AE上一动点(不与端点A重合,可以与端点E重合),将△APD沿PD折叠,得到点A的对称点为点F,连接BF.
(1)若点P在边AB中点时,则BF的长为 ;
(2)若△BPF为直角三角形时,求BF的长;
(3)将△APD绕点D逆时针旋转90°得到△DMN,点A的对应点为点M,点P的对应点为点N,连接FN.若△DFN为等腰三角形时,求BF的长.
25.折纸不仅是一项有趣的活动,也是一项益智的数学活动.今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论.
实践操作,解决问题
如图1,将矩形纸片ABCD沿对角线AC翻折,使点D′落在矩形ABCD所在平面内,边BC和AD′相交于点E,连接BD′.发现:结论①AE=EC;结论②BD′∥AC.
(1)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由;
(2)东京沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形(如图3所示).沿对称轴EF再次折叠后,得到的仍是轴对称图形,则京京折叠的矩形纸片的长宽之比为 ;
(3)新题探究:如图4所示,平行四边形ABCD中,∠ABC=60°,AB=2(AB≠BC).将△ADC沿对角线AC翻折.使点D′落在ABCD所在平面内,连接BD′,当△BCD′恰好为直角三角形时,BC的长度为 .
参考答案
【类型一:矩形的性质】
1.
【分析】根据相等垂直平分线的性质得到AB=AO,再由矩形的性质得到AO=6cm,则AB=AO=6cm.
【解答】解:∵AE垂直且平分线段BO,
∴AB=AO,
∵四边形ABCD是矩形,对角线AC与BD相交于点O,BD=12cm,
∴,
∴AB=AO=6cm,
故答案为:6.
2.
【分析】根据矩形的性质得到∠C=90°,CD=AB=4,BC=3,根据勾股定理得到BD5,得到DFBD,过F作FH⊥CD于H,根据相似三角形的性质即可得到结论.
【解答】解:在矩形ABCD中,∵∠C=90°,CD=AB=4,BC=3,
∴BD5,
∵BF=3DF,
∴DFBD,
过F作FH⊥CD于H,
∴FH∥BC,
∴△DFH∽△DBC,
∴,
∴,
∴FH,DH=1,
∵点E是CD的中点,
∴DE,
∴EH=DH=1,
∴EF=DF,
故选:B.
3.
【分析】连接CP,根据矩形的性质得到EF=CP,AP+EF的最小值即为AP+CP的最小值,当A,P,C三点共线时,AP+CP的值最小,且为AC的长度,根据勾股定理得到AC,于是得到结论.
【解答】解:连接CP,
∵四边形ABCD是矩形,
∴EF=CP,
∴AP+EF的最小值即为AP+CP的最小值,
当A,P,C三点共线时,AP+CP的值最小,且为AC的长度,
∵四边形ABCD是矩形,
∴AC,
∴AP+EF的最小值为,
故选:C.
4.
【分析】由矩形的性质可证明S△PEA=S△PFC,即可求解.
【解答】解:作PM⊥AD于M,交BC于N.如图2:
则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴CF=BE=2,
∴S△AEP=S△AMP,S△CFP=S△CNP,
∴S△AEP=S△CFPPF×CF6×2=6,
∴图中阴影部分的面积S阴=6+6=12.
故答案为:12.
5.(1)证明:在 ABCD中,OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形;
(2)解:∵四边形DEBF是矩形,
∴OE=OD,
∴∠ODE=∠OED,
∵∠AED+∠OED=180°,
∴∠OED=180°﹣∠AED=50°,
∴∠AOD=180°﹣∠ODE﹣∠OED=80°.
6.(1)解:如图①,连接BD,与AC交于点O,
∵四边形ABCD是矩形,
∴AC=BD,OBBD,OCAC,
∴OB=OC,
∴∠DBC=∠ACB=40°,
∵BE=AC,
∴BD=BE,
∴∠BDE=∠E,
∴∠E70°;
(2)证明:如图②,延长CF交AD延长线于点G,
∵AG∥BE,
∴∠GDF=∠E,∠G=∠ECF,
∵F是DE的中点,
∴DF=EF,
∴△DFG≌△EFC(AAS),
∴DG=EC,GF=CF.
∴BC+CE=AD+DG,即AG=BE,
∵BE=AC,
∴AG=AC,
又∵GF=CF,
∴AF⊥FC.
【类型二:矩形的判定】
7.
【分析】添加OD=5或∠ADC=90°,根据对角线互相平分且相等的四边形是矩形即可判断.
【解答】解:∵∠ABC=90°,AO=CO=5,
∴,AC=10,
①添加OD=5,
则BO=DO,BD=10,
∴四边形ABCD为平行四边形,
又AC=BD=10,
∴平行四边形ABCD为矩形;
②添加∠ADC=90°,
则,
∴BO=DO,BD=10,
∴四边形ABCD为平行四边形,
又AC=BD=10,
∴平行四边形ABCD为矩形;
添加OB=5,无法得到对角线互相平分,无法推出平行四边形ABCD为矩形;
故选:C.
8.
【分析】根据矩形的判定方法,逐一进行判断即可.
【解答】解:A、测量一组对边是否平行且相等,只能判断出这块鼠标垫是不是标准的平行四边形,故A选项不符合题意;
B、测量两组对边是否分别相等,只能判断出这块鼠标垫是不是标准的平行四边形,故B选项不符合题意;
C、测量其中的三个角是否都为直角,可以检验这块鼠标垫是不是标准的矩形,故C选项符合题意;
D、测量对角线是否相等,不能检验这块鼠标垫是不是标准的矩形,故D选项不符合题意;
故选:C.
9.(1)证明:∵ ABCD,
∴OA=OC,OB=OD,
∵BE=DF,
∴OB﹣BE=OD﹣DE,即OE=OF,
在△AOE和△COF中,
,
∴△AOE≌△COF(SAS).
(2)解:由(1)可得△AOE≌△COF.
∴OA=OC,OE=OF,
∴四边形AECF为平行四边形,
∵OA=OE,
∴OA=OE=OC=OF,
∴AC=EF,
∴四边形AECF是矩形.
10.(1)证明:∵O为AD的中点,
∴AO=DO,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAO=∠EDO,
又∵∠AOB=∠DOE,
∴△AOB≌△DOE(ASA),
∴AB=DE,
∴四边形ABDE是平行四边形,
∵∠BDC=90°,
∴∠BDE=90°,
∴平行四边形ABDE是矩形;
(2)解:如图,过点O作OF⊥DE于点F,
∵四边形ABDE是矩形,
∴DE=AB=2,ODAD,OB=OEBE,AD=BE,
∴OD=OE,
∵OF⊥DE,
∴DF=EFDE=1,
∴OF为△BDE的中位线,
∴,
∵四边形ABCD是平行四边形,
∴CD=AB=2,
∴CF=CD+DF=3,
在Rt△OCF中,由勾股定理得:OC,
即OC的长为.
【类型三:矩形的翻折问题】
11.
【分析】作AD⊥x轴,根据含 30°角直角三形的性质,及勾 股定理,求出AO,根据折叠的性质,求出AO,∠AOD,在Rt△ADO中,求出DO,AD,根据 第二象限内点的特征,即可求解,
【解答】解:过点A作AD⊥x轴,交x轴于点D,
在Rt△BAO 中,AB=6,∠AOB=30°,
∴BO=2AB=2×6=12,,
由折叠的性质可得:,
∠A'OB=∠AOB=30°,
即:∠AOD=2∠AOB=2×30°=60°,
在Rt△ADO 中,,,
∵点A在第二象限,,
故选:D.
12.
【分析】由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=4,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=3﹣x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
【解答】解:如图所示:∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=3,CD=AB=4,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=4,
在△ODP和△OEG中,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=3﹣x,DG=x,
∴CG=4﹣x,BG=4﹣(3﹣x)=1+x,
根据勾股定理得:BC2+CG2=BG2,
即32+(4﹣x)2=(x+1)2,
解得:x=2.4,
∴AP=2.4;
故答案为:2.4.
13.(1)证明:如图,矩形纸片折叠后,设A与F重合,过点G作GE⊥BC于点E,
由折叠的性质得:DH=BH,FD=BA,FG=AG,∠GHB=∠GHD,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AB=CD,AD=BC,AD∥BC,
∴∠DGH=∠GHB,
∴∠DGH=∠GHD,
∴GD=HD,
∴△DGH是等腰三角形.
(2)解:∵GD=HD,
∴GD=DH=BH,
∵AB=6,BC=8,
∴DF=CD=6,AD=8,
设BH=x,则HC=8﹣x,由勾股定理得:x2=(8﹣x)2+62,
解得:,
∴,
∴,
∴,
在Rt△GEH中,由勾股定理得:,
∴.
14.(1)解:∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∵∠BAM=32°,
∴∠AMB=90°﹣∠BAM=58°,
∵折叠,
∴∠AMN=∠NMC61°,
∵AD∥BC,
∴∠ANM=∠CMN=61°,
故答案为:61;
(2)证明:∵折叠,
∴CM=AM,AE=CD,∠AMN=∠CMN,∠E=∠D=90°,
∴△CDN≌△AEN(SAS),
∴AN=CN,
∵ABCD是矩形,
∴AD∥BC,
∴∠AMN=∠ANM,
∴∠ANM=∠AMN,
∴AM=AN,
∴AM=CM=AN=CN,
∴四边形AMCN为菱形;
(3)解:作MF⊥AN于点F,
∵AD∥BC,
∴△AMN和△ABM是等高的两个三角形
∴S△AMN:S△ABM=3:1=AN:BM,
∵BM=1,
∴AN=3,
∵AM=AN,
∴AM=3,
∵MF⊥AN,∠B=∠DAB=90°,
∴ABMF是矩形,
∴BM=AF=1,
∴根据勾股定理FM2,NF=2,
在Rt△MNF中,MN2.
【类型四:矩形的旋转问题】
15.
【分析】先利用旋转的性质得到∠ADC=∠D=90°,∠DAD′=α,再利用四边形内角和计算出∠BAD=66°,然后利用互余计算出∠DAD′,从而得到α的值.
【解答】解:∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,
∴∠ADC=∠D'=90°,∠DAD′=α,
∵∠ABC=90°,
∴∠BAD'=180°﹣∠2,
又∵∠2=∠1=114°,
∴∠BAD'=180°﹣114°=66°,
∴∠DAD′=∠BAD﹣∠BAD'=90°﹣66°=24°,
即α=24°.
故答案为:24.
16.(1)①证明:如图,
∵四边形形ABCD是矩形,
∴AD=BC,∠BAD=∠ABC=90°,
∵旋转,
∴AE=AB,EF=BC=AD,∠1=∠ABC=∠BAD=90°,
在△ABD和△EAF中,
,
∴△ABD≌△EAF(SAS),
∴∠2=∠EAF,BD=AF,
∵AB=AE,
∴∠3=∠2=∠EAF,
∴AF∥BD,
又∵AF=BD,
∴四边形ABDF是平行四边形;
②解:设HD=x,则AH=4﹣x,
∵四边形ABDF是平行四边形,
∴AB∥DF,AB=DF,
∴∠ADF=∠BAD=90°,
又∵∠1=90°,
∴∠ADF=∠1,
∵AE=AB,AB=DF,
∴AE=DF,
在△AEH和△FDH中,
,
∴△AEH≌△FDH(SAS),
∴HE=HD=x,
∵∠1=90°,
∴EA2+EH2=AH2,
又∵AH=4﹣x,EA=AB=3,EH=x,
∴32+x2=(4﹣x)2,
∴x,
∴AH=4﹣x.
(2)解:∵将矩形ABCD绕点A按逆时针方向旋转得到矩形AEFG,
∴旋转过程中,GF是定值,
当D,A,G三点共时,三角形DFG的面积最大,如图,
此时DG=8,
∴S△DFG12,
故答案为:12.
【类型五:矩形的动点问题】
17.
【分析】根据函数的图象、结合图形求出AB、BC的值,即可得出矩形ABCD的周长.
【解答】解:∵动点P从点B出发,沿BC、CD、DA运动至点A停止,而当点P运动到点C,D之间时,△ABP的面积不变,
函数图象上横轴表示点P运动的路程,x=4时,y开始不变,说明BC=4,x=9时,接着变化,说明CD=9﹣4=5,
∴AB=5,BC=4,
∴矩形ABCD的周长=2(AB+BC)=18.
故选:A.
18.解:(1)∵E,F是AC上两动点,分别从A,C两点以相同的速度向C、A运动,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴OD=OB,OA=OC,
∴OA﹣AE=OC﹣CF,
∴OE=OF,
∴四边形DEBF是平行四边形;
(2)点E,F在AC上运动过程中,以D、E、B、F为顶点的四边形能为矩形.理由如下:
分为两种情况:
①∵四边形DEBF是矩形,
∴BD=EF=10cm,
即AE=CF=0.5t cm,
则16﹣0.5t﹣0.5t=10,
解得:t=6;
②当E到F位置上,F到E位置上时,AE=CF=0.5t cm,
则0.5t﹣10+0.5t=16,
解得:t=26,
即当运动时间t=6s或28s时,以D、E、B、F为顶点的四边形是矩形.
19.解:(1)如图所示,连接BQ,
∵四边形ABCD是矩形,
∴∠BAQ=∠ABE=90°,∠PEQ=90°,
∴四边形ABEQ是矩形,
当点P和点B重合时,
QE=AB=3,BE=2,
在Rt△QBE中,
BQ,
故答案为:;
(2)如图,
设AP=x,则BP=3﹣x,
在Rt△APQ中,AP2+AQ2=PQ2,
∴PQ2=52+x2,
在Rt△PBE中,PB2+BE2=PE2,
∴PE2=(3﹣x)2+22,
在Rt△ECQ中,EC2+CQ2=EQ2,
∴PQ2=32+32,
∵∠PEQ=90°,
∴PE2+EQ2=PQ2,
∴22+(3﹣x)2+32+32=52+x2,
故x=1,
即AP长为1;
(3)证明:如图2,过点P作PH⊥BC于点H,
则PH=3,
同理可得∠EPH=∠QEC,
∵EC=BC﹣BE=3,
∴PH=EC,
又∠PHE=∠C=90°,
∴△PHE≌△ECQ(ASA),
∴PE=HE,
∴△PQE是等腰直角三角形;
(4)①如图所示,当点P在BE上时,
∵QE=QF=3,AQ=BE=2,
在Rt△AQF中,
AF,
则BF=3,
∵PE=t,
∴BP=2﹣t,PF=PE=t,
在Rt△PBF中,PF2=PB2+FB2,
∴t2=(3)2+(2﹣t)2,
解得:t,
t时,点F在矩形内部,
∴0<t,符合题意,
②当P点在AB上时,当F,A重合时符合题意,此时如图,
则PB=t﹣BE=t﹣2,PE=AP=AB﹣PB=3﹣(t﹣2)=5﹣t,
在Rt△PBE中,PE2=PB2+BE2,
∴(5﹣t)2=(t﹣2)2+22,
解得t,
③当点P在AD上,当F,D重合时,此时点Q与点C重合,
则PFQE是正方形,此时t=2+3+2=7,
∴0<t或t或t=7.
【类型六:与矩形有关的作图题】
20.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
21.解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,当点M与A重合时,MN的长最大,最大值AB=4;
如图2中,当点E以D重合时,连接BM,设BD,AC交于点O,MN的长最小,设BM=DM=x,则有x2=42+(8﹣x)2,
解得x=5,
∵∠BAD=90°,AB=4,AD=8,
∴BD4,
∴OB=OD=2,
∴OM=ON,
∴MN=2,
∴2MN≤4.
故答案为:2MN≤4.
22.解:(1)如图甲所示,平行四边形ABCD即为所求(答案不唯一).
(2)如图乙所示,矩形AEBF即为所求(答案不唯一).
【类型七:矩形综合题】
23.解:(1)∵,
∴,
∴∠BEM=90°,
如图1,取BM的中点O,连接EO,
∴,
∴△BEO为等边三角形,
∴∠BME=30°,
∴∠ABM=60°,
∴∠ABP=∠PBM=30°,
故答案为:30;
(2)①四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠C=90°,
由折叠性质得:AB=BM,∠PMB=∠BMQ=∠A=90°,
∴BM=BC,
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴MBQ=∠CBQ,QM=QC,
同法(1)可得:∠MBC=30°,
∴∠MBQ=∠CBQ=15°,
∴∠ABM=90°﹣30°=60°,
∴∠APM=180°﹣60°=120°,
∴∠QPD=180°﹣120°=60°,
在Rt△ABP中,BP=2AP,
根据勾股定理:BP2﹣AP2=AB2,
即3AP2=16,
解得:,
∴,
在Rt△PDQ中,PQ=2PD,
根据勾股定理:DQ2=PQ2﹣PD2,即DQ2=3PD2,
∴,
∴,
故答案为:15,;
②∠MBQ=∠CBQ,理由如下:
∵BM=BC,BQ=BQ,
∴Rt△BQM≌Rt△BQC(HL),
∴∠MBQ=∠CBQ;
(3)当点Q在点F的下方时,如图3.1,
∵FQ=lcm,DF=FC=2cm,AB=4cm,
∴QC=CD﹣DF﹣FQ=4﹣2﹣1=l(cm),DQ=DF+FQ=2+1=3(cm),
由(2)可知,QM=QC,
设AP=PM=x,PD=4﹣x,
∴PD2+DQ2=PQ2,
即(4﹣x)2+32=(x+1)2,
解得:,
∴;
当点Q在点F的上方时,如图3.2,
∵FQ=lcm,DF=FC=2cm,AB=4cm,
∴QC=3cm,DQ=lcm,
由(2)可知,QM=QC,
设AP=PM=x,PD=4﹣x,
∴PD2+DQ2=PQ2,
即(4﹣x)2+12=(x+3)2,
解得:,
∴.
综上所述,或.
24.解:(1)连接AF交DP于点M,
∵将△APD沿PD折叠,得到点A的对称点为点F,
∴DP垂直平分AF,
∵P是AB的中点,
∴PM是△ABF的中位线,
∴BF=2PM,
∵AD=6,APAB=4,
∴DP2,
∵,
∴AM,
∴PM,
∴BF.
故答案为:;
(2)若△BPF为直角三角形.
①当∠PBF=90°时,不存在.
②当∠PFB=90°时(如图4),
∵将△APD 沿PD折叠,得到点A的对称点为点F.
∴∠DFP=∠B=90°,
∴∠DFP+∠PFB=180°,
∴点D,F,B共线.即点F在矩形对角线DB上.
∵AD=6,AB=8,∠A=90°,
∴BD10.
∵DF=DA=6,
∴BF=10﹣6=4.
此时AP=PF=3.
③当∠BPF=90°时(如图 5),
∵∠A=90°,∠DFP=90°,
∴四边形ADFP是矩形.
∴点F在DC边上,
∵BE=2,EF=6,∠BEF=90°,
∴,
∴BF的长为4或;
(3)若△DFN为等腰三角形.
①当DF=DN时,不存在.
②当 FD=FN时(如图6),
设∠ADP=x,
∵将△APD 沿PD折叠,得到点A的对称点为点F.
∴∠ADP=∠PDF=x,
∵将△APD 绕点D逆时针旋转90°得到△DMN.
∴∠PDN=90°,
∴∠FDN=∠FND=∠DPA=90°﹣x,
∴∠FND=∠MND=90°﹣x,
即∠FND与∠MND重合.
∴点F与点M重合,
∴.
③当ND=NF时(如图7),
过点N作NH⊥DF垂足为H.
∵∠ADP=∠PDF=∠MDN,
∴∠ADP=∠DNH,
∵∠A=∠DHN=90°,DN=DP,
∴△NDH≌△DPA(AAS),
∴,
由(2)可知,当AP=3 时,BF=4.
∴BF的长为4或.
25.解:(1)AE=EC,BD′∥AC,理由如下,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAC=∠EAC,
∵折叠,
∴AD=AD′,∠DAC=∠D′AC,
∴∠EAC=∠ECA,
∴AE=EC,
∵折叠,
∴AD=AD′,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD′=BC,
∵EC=EA,
∴AD′﹣AE=BC﹣CE,即BE=ED′,
∴,
又∵,∠AEC=∠BED′,
∴∠EAC=∠ED′B,
∴BD′∥AC;
(2)当点D′与B点不重合时,如图,
依题意,EF=ED′=BE,AE=EC,∠EFC=∠AFE=90°,
设∠ACB=α,则∠EAF=∠ACB=∠BAE,
∵∠ACB+∠BAC=90°,
∴α+2α=90°,
解得:α=30°,
∴,
在Rt△ABC中,,
∴矩形纸片的长宽之比为,
当点D′与B点重合时,如图,
此时ABCD是正方形,
∴矩形纸片的长宽之比为1:1,
综上矩形纸片的长宽之比1:1或;
(3)当∠CBD′=90°时,如图,设CD′与AB交于点E,
由(1)可得BD′∥AC,
∴∠ACB=180°﹣∠CBD′=90°,
在Rt△ABC中,∵∠ABC=60°,AB=2,
∴∠BAC=30°,
∴;
如图,当∠CD′B=90°时,由(1)可得BD′∥AC,
∴∠ACD′=180°﹣∠BD′C=90°,
∵折叠,
∴∠ACD=∠ACD′=90°,
∴D,C,D′三点共线,
∵四边形ABCD是平行四边形,∠ABC=60°,AB=2,
∴∠D=60°,CD=AB=2,
∴∠DAC=30°,
在Rt△ACD中,A D=2 C D=4,
∴BC=AD=4;
如图,当∠BCD′=90°时,
∵∠ABC=60°,
∴∠BEC=30°,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DCA=∠EAC,
∵折叠,
∴AD=AD′,∠DCA=∠ECA,
∴∠EAC=∠ECA,
∴AE=EC,
设BC=m,
∴BE=2m,,
∴,
∴,
∴;
如图,当∠BCD′=90°时,同理可得∠CDE=∠D=∠ABC=60°,∠CED=30°=∠AEB,CD=CD′=2=AB,
∴D′E=4,,
同理可得:AE=CE,AD′=AD=BC,
∴BE=D′E=4,
∴;
综上所述:BC的长度为1或4或或.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
