苏科版八年级数学下册 9.4.2菱形 复习题(含解析)
文档属性
| 名称 | 苏科版八年级数学下册 9.4.2菱形 复习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 07:46:16 | ||
图片预览

文档简介
9.4.2菱形复习题
【类型一:菱形的性质】
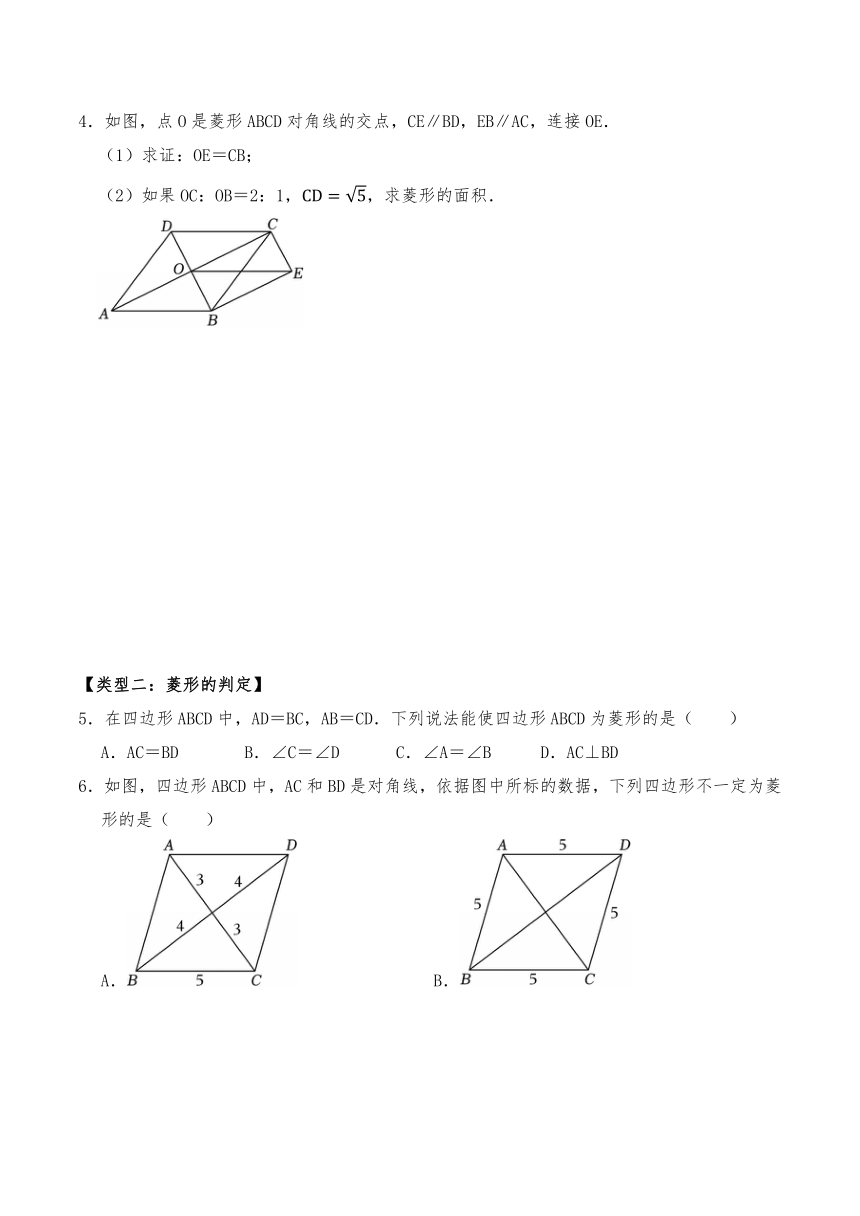
1.如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,AF⊥BC于点F,交BD于点P.若AB=6,则DP的长为( )
A. B. C. D.
2.如图,在菱形ABCD中,AB∥y轴,且B(﹣1,﹣2),C(3,1),则点A的坐标为 .
3.如图,在菱形ABCD中,直线MN分别交AB、CD、AC于点M、N和O.且AM=CN,连接BO.若∠OBC=60°,则∠DAC为( )
A.65° B.30° C.25° D.20°
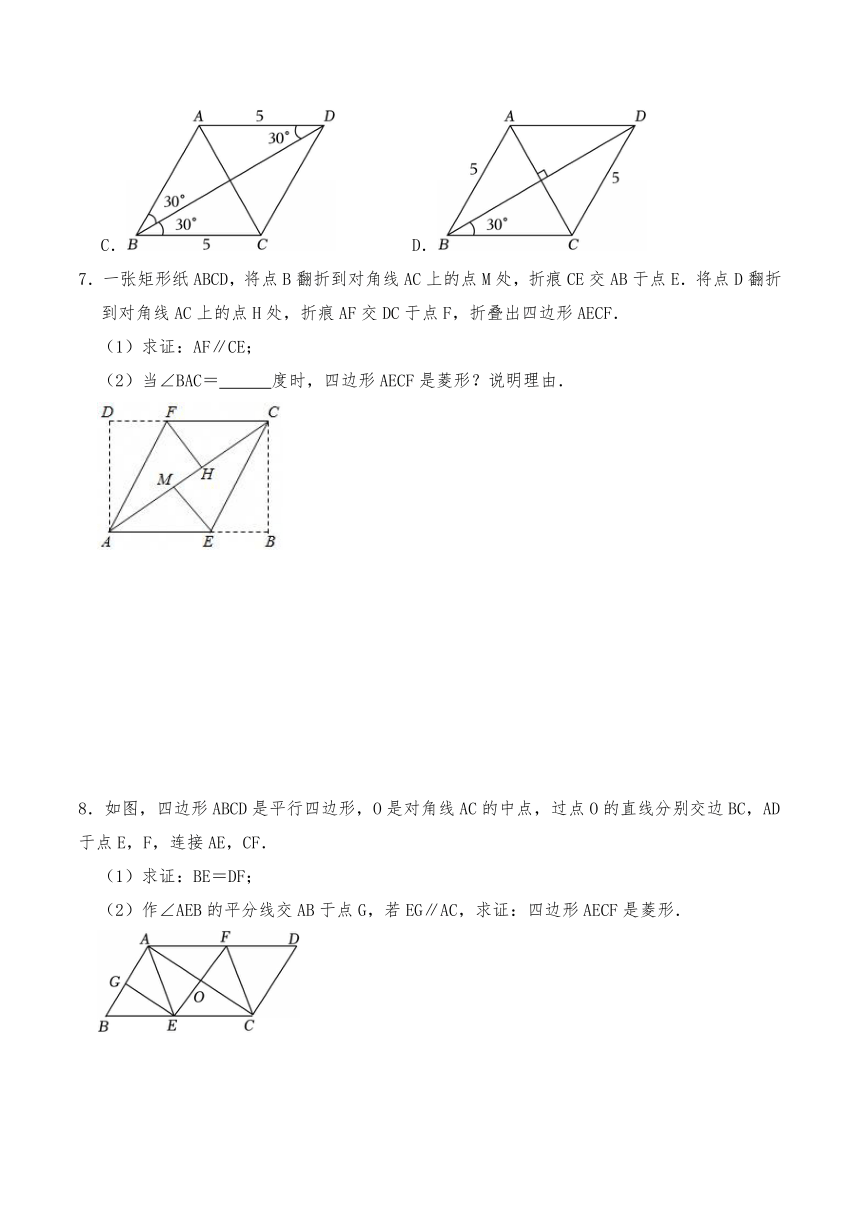
4.如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE.
(1)求证:OE=CB;
(2)如果OC:OB=2:1,,求菱形的面积.
【类型二:菱形的判定】
5.在四边形ABCD中,AD=BC,AB=CD.下列说法能使四边形ABCD为菱形的是( )
A.AC=BD B.∠C=∠D C.∠A=∠B D.AC⊥BD
6.如图,四边形ABCD中,AC和BD是对角线,依据图中所标的数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
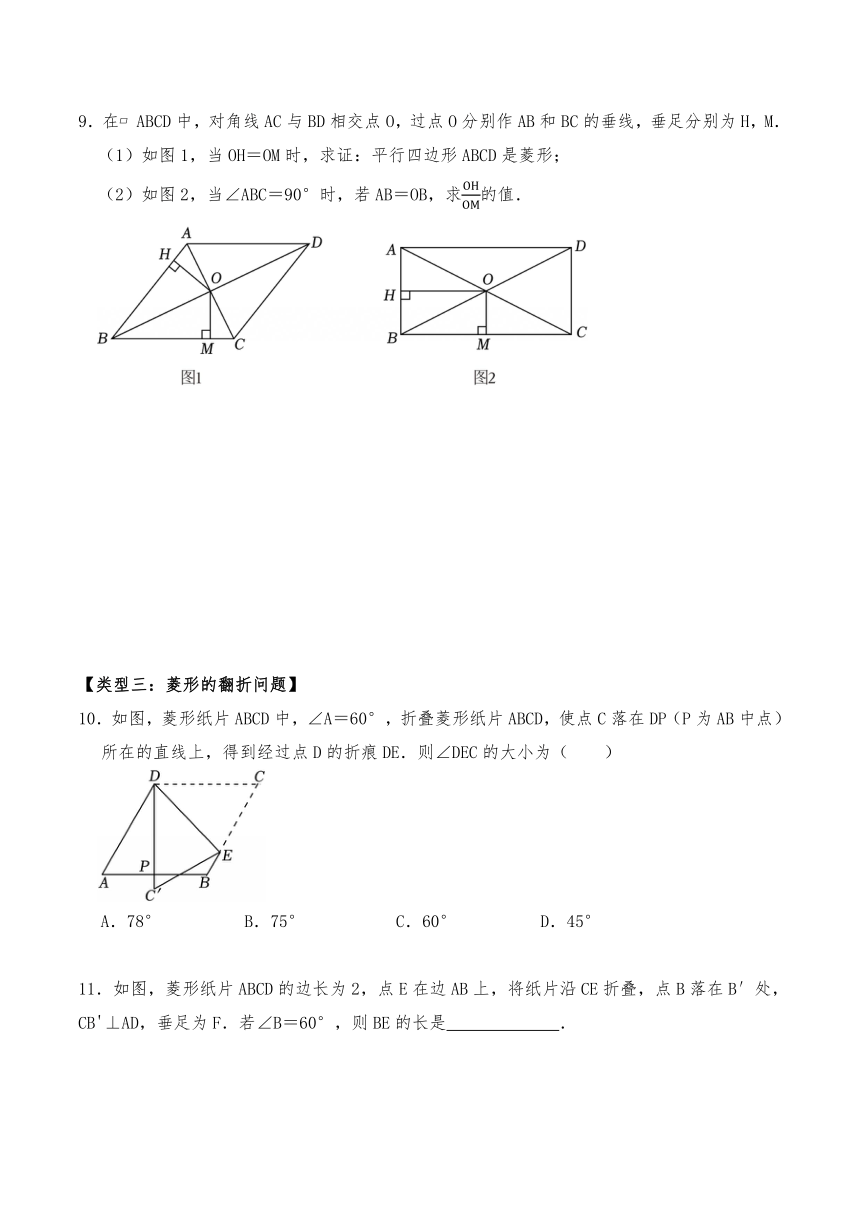
7.一张矩形纸ABCD,将点B翻折到对角线AC上的点M处,折痕CE交AB于点E.将点D翻折到对角线AC上的点H处,折痕AF交DC于点F,折叠出四边形AECF.
(1)求证:AF∥CE;
(2)当∠BAC= 度时,四边形AECF是菱形?说明理由.
8.如图,四边形ABCD是平行四边形,O是对角线AC的中点,过点O的直线分别交边BC,AD于点E,F,连接AE,CF.
(1)求证:BE=DF;
(2)作∠AEB的平分线交AB于点G,若EG∥AC,求证:四边形AECF是菱形.
9.在 ABCD中,对角线AC与BD相交点O,过点O分别作AB和BC的垂线,垂足分别为H,M.
(1)如图1,当OH=OM时,求证:平行四边形ABCD是菱形;
(2)如图2,当∠ABC=90°时,若AB=OB,求的值.
【类型三:菱形的翻折问题】
10.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A.78° B.75° C.60° D.45°
11.如图,菱形纸片ABCD的边长为2,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB'⊥AD,垂足为F.若∠B=60°,则BE的长是 .
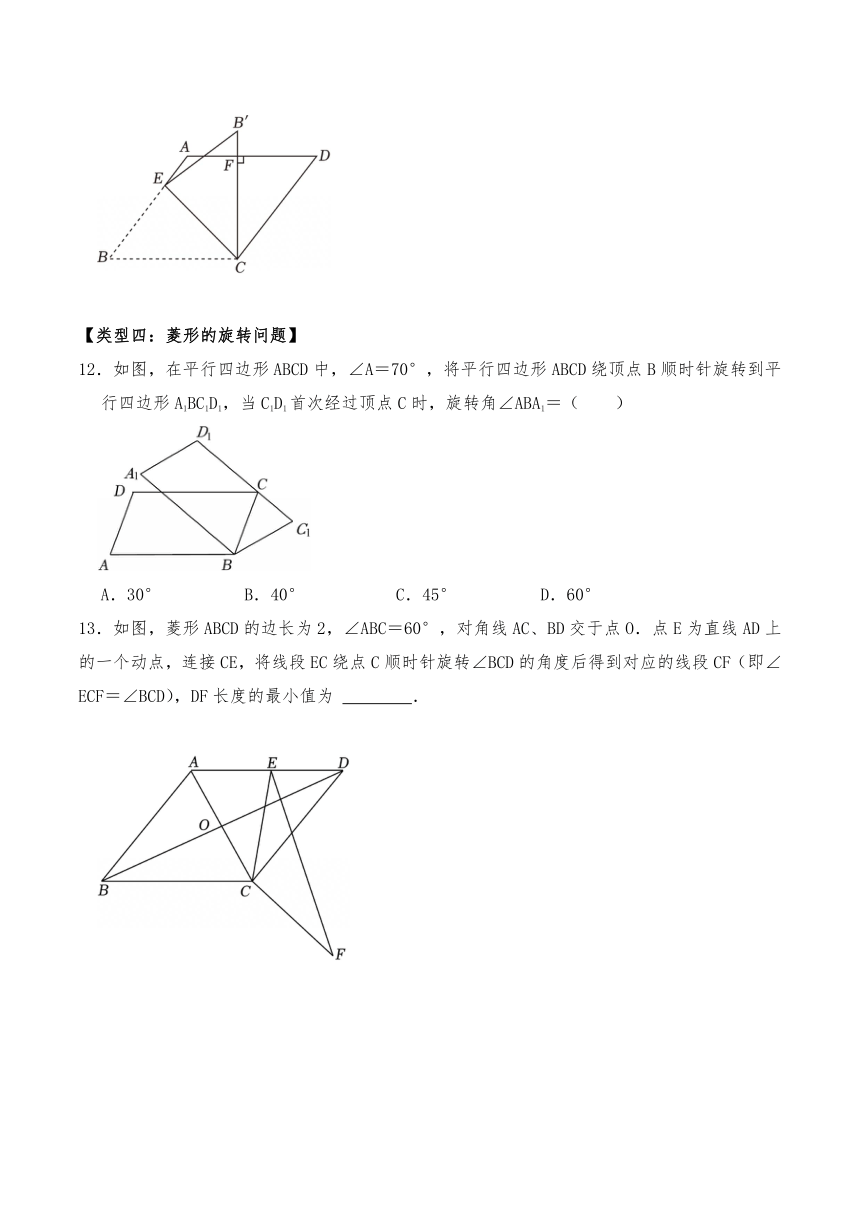
【类型四:菱形的旋转问题】
12.如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=( )
A.30° B.40° C.45° D.60°
13.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为 .
【类型五:菱形的动点问题】
14.如图1,在菱形ABCD中,点P沿A﹣B﹣C方向从点A移动到点C,设点P的移动路程为x,线段AP的长为y,点P在运动过程中y与x的变化关系如图2所示,点P运动到BC边上时,当x=18,y的值最小为12,则a的值是 .
15.如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)DH= ;DM= ;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
【类型六:菱形在一次函数中的存在性问题】
16.已知,如图,O为坐标原点,在四边形OABC中,BC∥OA,BC=24,A(26,0),C(0,12),点D是OA的中点,动点P在线段BC上以每秒2个单位长度的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当P运动 秒,四边形PDAB是平行四边形.
(2)在直线CB上是否存在一点Q,使得以O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.
17.如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒3个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,请直接写出所有满足条件的点N的坐标.
【类型七:与菱形有关的作图题】
18.(1)图1是在Rt△ABC中,∠B=90°,用直尺和圆规作矩形ABCD,作法是“以点A为圆心,BC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D“,请判断所作的四边形ABCD是不是矩形,并说明理由.
(2)如图2,在矩形ABCD的边AB上任取一点E,O是AC中点,在BC、CD、DA上各找一点F、G、H,使得四边形EFGH是菱形.(要求:利用直尺和圆规,作出图形,保留作图痕迹)
19.如图,在矩形ABCD中,BD是对角线.
(1)在AD边上确定一点E,将△BED沿BD翻折后,点E的对应点F恰好落在BC边上;(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,连接BE、DF,判断四边形BEDF的形状.
20.在平行四边形ABCD中,E、F分别是线段AD、BC上的点,请用直尺和圆规作菱形ABFE.
要求:
(1)用两种不同方法,不写作图过程,保留作图痕迹;
(2)选择其中一种给出证明过程.
21.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4.求作菱形AEFG,使点E在边AD上,点F,G在边BC上.
小宁的作法1.如图②,在边AD上取一点E.
2.以点A为圆心,AE长为半径画弧,交BC于点G.
3.在BC上截取GF=AE,连接EF,则四边形AEFG为所求作的菱形.
(1)证明小宁所作的四边形AEFG是菱形.
(2)小宁进一步探索,发现可作出的菱形的个数随着点E的位置变化而变化.请你继续探索,直接写出菱形的个数及对应的AE的长的取值范围.
【类型八:菱形综合题】
22.邻边长分别为1,a(a>1)的平行四边形纸片,如图那样折一下,剪下一个边长等于1的菱形(称为第一次操作);再把剩下的平行四边形如图那样折一下,剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作);再把剩下的平行四边形如此反复操作下去.若在第三次操作后,剩下的平行四边形为菱形,则a的值 .
23.如图,E为菱形ABCD对角线AC上一点,直线DE交射线AB于点F,AD=10,AC=8.
(1)求此菱形的面积;
(2)当△BEF是直角三角形时,求AE的长.
参考答案
【类型一:菱形的性质】
1.
【分析】先由菱形的性质得到AD=AB=BC=6,AC⊥BD,AC=2OA,再证明△ABC是等边三角形,则AC=AB=6,进而得到OA=3,由三线合一定理得到∠OAP=30°,则可求出,利用勾股定理得到,则.
【解答】解:∵四边形ABCD是菱形,
∴AD=AB=BC=6,AC⊥BD,AC=2OA,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6,
∴OA=3,
∵AF⊥BC,
∴∠OAP=30°,
∴,
在Rt△AOD中,由勾股定理得,
∴,
故选:C.
2.
【分析】过B作BM⊥DC于点M,与y轴交于点N,由勾股定理求出BC=5,再由菱形的性质得AB=BC=5,即可解决问题.
【解答】解:如图,过B作BM⊥DC于点M,与y轴交于点N,
∵B(﹣1,﹣2),C(3,1),
∴BN=1,BF=EM=2,MN=3,CE=1,
∴BM=MN+BN=3+1=4,CM=CE+EM=1+2=3,
∵四边形ABCD是菱形,
∴AB=BC,
在Rt△BCM中,由勾股定理得:BC5,
∴AB=BC=5,
∴AF=AB﹣BF=5﹣2=3,
∵AB∥y轴,
∴点A的坐标为(﹣1,3),
故答案为:(﹣1,3).
3.
【分析】先由菱形性质得出AB∥CD,BC∥AD,BA=BC.结合AM=CN,证明△OAM≌△OCN(ASA),则OA=OC,因为∠OBC=60°,所以运用三角形内角和性质来计算,即可作答.
【解答】解:∵四边形ABCD是菱形,
∴AB∥CD,BC∥AD,BA=BC.
∴∠OMA=∠ONC,∠OAM=∠OCN,∠DAC=∠OCB.
在△OAM和△OCN中,
,
∴△OAM≌△OCN(ASA).
∴OA=OC.
∴BO⊥AC.
∴∠BOC=90°.
∵∠OBC=60°,
∴∠OCB=180°﹣∠BOC﹣∠OBC=30°.
∴∠DAC=∠OCB=30°.
故选:B.
4.(1)证明:点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,
∴AC⊥BD,四边形OCEB是平行四边形,∠COB=90°,
∴四边形OCEB是矩形,
∴OE=CB;
(2)解:∵四边形ABCD是菱形,OC:OB=2:1,,
∴,OC=2OB,
由(1)知,AC⊥BD,
在Rt△BOC中,由勾股定理得BC2=OC2+OB2,
即5=OC2+(2OC)2,
∴CO=2,OB=1.
∵四边形ABCD是菱形,
∴AC=4,BD=2,
∴菱形ABCD的面积.
【类型二:菱形的判定】
5.
【分析】先证四边形ABCD是平行四边形,再由菱形的判定和矩形的判定分别对各个选项进行判断即可.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
A、∵AC=BD,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、由AB=CD,不能判定四边形ABCD为菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵AC⊥BD,
∴平行四边形ABCD为菱形,故选项D符合题意;
故选:D.
6.
【分析】AC与BD交于点O,由OC=OA=3,OB=OD=4,可证明四边形ABCD是平行四边形,由OB2+OC2=BC2=25,证明∠BOC=90°,则四边形ABCD是菱形,可判断A不符合题意;由AB=AD=CB=CD=5,可证明四边形ABCD是菱形,可判断B不符合题意;由AD∥BC,AD=BC=5,证明四边形ABCD是平行四边形,由∠ADB=∠ABD=30°,得AB=AD,则四边形ABCD是菱形,可判断C不符合题意;若AB∥CD,则四边形ABCD是菱形;C′D与AB不平行,则四边形ABC′D不是菱形,可判断D符合题意,于是得到问题的答案.
【解答】解:如图1,AC与BD交于点O,
∵OC=OA=3,OB=OD=4,
∴四边形ABCD是平行四边形,
∵BC=5,
∴OB2+OC2=42+32=25,BC2=52=25,
∴OB2+OC2=BC2,
∴△BOC是直角三角形,且∠BOC=90°,
∴AC⊥BD,
∴四边形ABCD是菱形,
故A不符合题意;
如图2,∵AB=AD=CB=CD=5,
∴四边形ABCD是菱形,
故B不符合题意;
如图3,∵∠ADB=∠CBD=30°,
∴AD∥BC,
∵AD=BC=5,
∴四边形ABCD是平行四边形,
∵∠ADB=∠ABD=30°,
∴AB=AD,
∴四边形ABCD是菱形,
故C不符合题意;
若AB∥CD,
∵AB=CD=5,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
若C′D=AB=5,但C′D与AB不平行,则四边形ABC′D不是菱形,
∴四边形ABCD不一定是菱形,
故D符合题意,
故选:D.
7.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
由翻折知,∠DAF=∠HAF∠DAC,∠BCE=∠MCE∠BCA,
∴∠HAF=∠MCE,
∴AF∥CE;
(2)解:当∠BAC=30°时四边形AECF为菱形,理由如下:
∵四边形ABCD是矩形,
∴∠D=∠BAD=90°,AB∥CD,
由(1)得:AF∥CE,
∴四边形AECF是平行四边形,
∵∠BAC=30°,
∴∠DAC=60°.
∴∠ACD=30°,
由折叠的性质得∠DAF=∠HAF=30°,
∴∠HAF=∠ACD,
∴AF=CF,
∴四边形AECF是菱形;
故答案为:30.
8.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,AD=BC,
∴∠FAO=∠ECO,
在△FAO与△CEO中,
,
∴△FAO≌△CEO(ASA),
∴AF=CE,
∴AD﹣AF=BC﹣CE,
即BE=DF;
(2)∵AF=CE,AF∥CE,
∴四边形AECF是平行四边形,
∵EG∥AC,
∴∠GEB=∠ACE,∠GEA=∠EAC,
∵∠AEB的平分线交AB于点G,
∴∠GEB=∠GEA,
∴∠ACE=∠EAC,
∴AE=EC,
∴ AECF是菱形.
9.(1)证明:∵OH⊥AB,OM⊥BC,OH=OM,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,BD=AC,
∴OA=OC=OB=OD,
∵AB=OB,
∴△ABC是等边三角形,
∴∠ABO=60°,
∴∠OBM=30°,
∵OH⊥AB,OM⊥BC,
∴四边形OHBM是矩形,
∴OH=BM,OB=2OM,
∴BMOM,
∴.
【类型三:菱形的翻折问题】
10.
【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选:B.
11.
【分析】作EH⊥BC于点H,则∠BHE=∠CHE=90°,求出∠ECB=45°,得到EH=CH,在Rt△EBH中,用BE表示EH,BH,再利用BH+CH=BC列方程解出即可.
【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,
由折叠得BC=B′C=2,∠BCE=∠B′CE,
∵四边形ABCD是菱形,
∴BC∥AD,DC=BC=2,∠B=∠D=60°,
∵CB′⊥AD于点F,
∴∠BCB′=∠CFD=90°,
∴∠BCE=∠B′CE∠BCB′90°=45°,
∵∠B=60°,
∴∠DCF=30°,
∴DFDC2=1,
∴∠HEC=∠BCE=45°,
∴CH=EH,
在Rt△EBH中,
∵sinB,cosB,
∴CH=EHBE,BHBE,
∴BEBE=2,
∴BE,
故答案为:.
【类型四:菱形的旋转问题】
12.
【分析】根据平行四边形的性质及旋转的性质可知∠A=∠C=∠C1=70°,BC=BC1,然后可得∠BCC1=∠C1=70°,则有∠CBC1=40°,进而问题可求解.
【解答】解:∵四边形ABCD是平行四边形,∠A=70°,
∴∠A=∠C=70°,
由旋转的性质可得∠C=∠C1=70°,BC=BC1,∠ABA1=∠CBC1,
∴∠BCC1=∠C1=70°,
∴∠ABA1=∠CBC1=40°.
故选:B.
13.
【分析】连接BE,作BH⊥AD,由旋转的性质可得△DCF≌△BCE,把求DF的最小值转化为求BE的最小值,再根据垂线段最短可得答案.
【解答】解:连接BE,作BH⊥AD交DA的延长线于H,
菱形ABCD中,∠ABC=60°,
∴∠BCD=120°.
∵∠ECF=120°,
∴∠BCD=∠ECF,
∴∠BCE=∠DCF
由旋转可得:EC=FC,
在△BEC和△DFC中,
,
∴△DCF≌△BCE(SAS),
∴DF=BE,
即求DF的最小值转化为求BE的最小值.
∵在Rt△AHB中,∠BAH=60°,AB=2,
∴BH=2sin60°,
当E与H重合时,BE最小值是,
∴DF的最小值是.
故答案为:.
【类型五:菱形的动点问题】
14.
【分析】根据菱形的性质,再结合P运动时y随x的变化的关系图象,运用勾股定理即可求解.
【解答】解:如图1,过A点作AE⊥BC于E,
根据图2知:当点P与点E重合时,AB+BP=18,AP=12,
∴AB+BE=18,AE=12,
设AB=m,则BE=18﹣m,
在Rt△ABE中,AE2+BE2=AB2,
∴122+(18﹣m)2=m2,
解得:m=13,
∴AB=BC=CD=AD=13,BE=5,
∴EC=BC﹣BE=13﹣5=8,
当点P到达点C时,AP=AC=a,
在Rt△ACE中,AC2=AE2+EC2,即a2=122+82=208,
∵a>0,
∴a=4,
故答案为:4.
15.解:(1)在Rt△ADH中,AD=5,AH=3,
∴DH4,
在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵AC是菱形ABCD的对角线,
∴∠ACD=∠ACB,CD=CB,
在△DCM和△BCM中,
,
∴△DCM≌△BCM(SAS),
∴DM=BM,
在Rt△BHM中,BM=DM,HM=DH﹣DM=4﹣DM,BH=AB﹣AH=2,
根据勾股定理得,DM2﹣MH2=BH2,
即:DM2﹣(4﹣DM)2=4,
∴DM;
故答案为:4,;
(2)在△BCM和△DCM中,
,
∴△BCM≌△DCM(SAS),
∴BM=DM,∠CDM=∠CBM=90°
①当P在AB之间时,0<t,S(5﹣2t)t.
②当P在BC之间时,t<5,S(2t﹣5)t,
综上,S与t之间的函数关系式为S;
(3)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四边形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM(AAS),
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=2,
∴BP=2BH=4,
∵AB=5,
∴AP=1,
∴t.
【类型六:菱形在一次函数中的存在性问题】
16.解:(1)∵A(26,0),C(0,12),
∴OA=26,OC=8,
∵点D时OA的中点,
∴OD=1OA=13,
由运动知,PC=2t,
∵BC=24,
∴BP=BC﹣PC=24﹣2t,
∵四边形PDAB是平行四边形,
∴PB=AD=13,
∴24﹣2t=13,
解得t=5.5,
∴当t值为5.5时,四边形PDAB是平行四边形.
故答案为:5.5;
(2)存在,分三种情况:
①当Q点在P点的右边时,如图,
∵四边形ODQP是菱形,
∴OD=OP=PQ=13,
∴在Rt△OPC中,由勾股定理得:PC=5,
∴2t=5,
解得t=2.5,
∴Q(18,12);
②当Q点在P点左侧且在BC线段上时,如图,
同理①得PC=18,
即2t=18,
解得t=9,
∴Q(5,12);
③当Q点在P点左侧且在BC延长线上时,如图3,
同理①求出QC=5,PC=13﹣5=8,
即2t=8,
解得t=4,
∴Q(﹣5,12);
综上,t=2.5时,Q(18,12),t=9时,Q(5,12),t=4时,Q(﹣5,12).
17.解:(1)若点P在点A的左侧,四边形PABQ为平行四边形,PA=QB,
由题意得4﹣3t=t,
解得t=1,
若点P在点A的右侧,四边形PAQB为平行四边形,PA=QB,
∴3t﹣4=t,
解得t=2,
综上:t=1或2时,以A,B,P,Q为顶点的四边形为平行四边形.
(2)N点坐标为(﹣5,3),(5,3),(0,﹣3),.
∵点A(4,0),C(0,3),
∴AO=4,OC=3,
∴AC5,
如图,以AC为边,四边形ACMN是菱形,
∵C(0,3),
∴N(0,﹣3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(5,3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(﹣5,3);
如图,以AC为对角线,四边形ACNM是菱形,
设CM=AM=CN=x,
∴OM=4﹣x,
∵OC2+OM2=CM2,
∴32+(4﹣x)2=x2,
∴,
∴CN,
∴N(,3);
综上所述,以A、C、M、N为顶点的四边形是菱形时,点N的坐标为(﹣5,3),(5,3),(0,﹣3),.
【类型七:与菱形有关的作图题】
18.解:(1)如图1中,四边形ABCD是矩形.
理由:∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴四边形ABCD是矩形;
(2)四边形EFGH即为所求.
19.解:(1)所作的图形如图:
;
(2)证明:四边形BEDF是菱形.理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,
由翻折知,BE=BF,
由作图知,BE=DE,
∴DE=BF,
∴四边形BEDF是平行四边形,
∵BE=BF,
∴四边形BEDF是菱形.
20.解:(1)如图1、如图2,菱形ABFE为所作;
(2)如图1:∵四边形ABCD为平行四边形,
∴AD∥BC,
∵AE=AB,BF=AB,
∴AE=BF,
而AE∥BF,
∴四边形ABFE为平行四边形,
∵AB=AE,
∴四边形ABFE为菱形;
如图2:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AEB=∠FBE,
∵BE平分ABC,
∴∠FBE=∠ABE,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得BF=BA,
由图1的结论得到四边形ABFE为菱形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形.
(2)解:如图①中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图象可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
【类型八:菱形综合题】
22.
【分析】根据题意,进行分类讨论,再根据菱形的性质,列出方程求解即可.
【解答】解:①如图,经历三次折叠后,四边形IJHF为菱形,
∵四边形ABCD为菱形,
∴AB=AD=BC=CD=1,
∴DF=CE=a﹣1,
∵四边形GCEH为菱形,
∴GC=CE=a﹣1,
∴DG=FH=1﹣(a﹣1)=2﹣a,
∵四边形DGJI为菱形,
∴DI=DG=2﹣a,
∴IF=a﹣1﹣(2﹣a)=2a﹣3,
∵四边形IJHF为菱形,
∴IF=HF,即2﹣a=2a﹣3,
解得:;
②如图,经历三次折叠后,四边形DIHF为菱形,
∵四边形ABCD为菱形,
∴AB=AD=BC=CD=1,
∴DF=CE=a﹣1,
∵四边形JCEG,IJGH,DIHF都为菱形,
∴,
∴,
解得:;
③如图,经历三次折叠后,四边形FIJH为菱形,
∵四边形ABCD,DCEF为菱形,
∴AB=AD=BC=CD=CE=DF=EF=1,
∴FH=a﹣2,
∵四边形FIJH,IEGJ都为菱形,
∴,
∴,
解得:;
④如图,经历三次折叠后,四边形HGIJ为菱形,
∵四边形ABCD,DCEF,FEGH,HGIJ都为菱形,
∴AB=AD=DF=FH=1,
∴HJ=a﹣3,
∴HJ=IJ,
∴a﹣3=1,
解得:a=4;
综上:a的值为或4或或.
23.解:(1)连接BD,交AC于点O,
∵四边形ABCD是菱形,
∴BO=DO,AOAC=4,AC⊥BD,
∴OD2,
∴BD=4,
∴菱形的面积 8 480;
(2)①当∠EFB=90°时,如图1,
∵∠EFB=90°,
∴菱形的面积=10 DF=80,
∴DF=8,
∴AF6,
∴BF=4,
∵AC垂直平分BD,
∴DE=BE,
∵BE2=FE2+BF2,
∴EF2+42=(8﹣EF)2,
得EF=3,
在△AEF中,AE3,
②当∠BEF=90°时,如图2,连接BD交AC于O,当点E在AO上时,
则△EDB是等腰直角三角形,BD=4,
∴OE=2,
∴AE=2;
当点E在OC上时,同理可求AE=6,
③当∠FBE=90°时,如图3,
∵AE2=BE2+AB2,AE OB=BA BE,
∴AE2=BE2+100,2AE=10BE,
∴AE2=(AE)2+100,
∴AE=5,
综上:AE的长为3或2或6或5.
【类型一:菱形的性质】
1.如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,AF⊥BC于点F,交BD于点P.若AB=6,则DP的长为( )
A. B. C. D.
2.如图,在菱形ABCD中,AB∥y轴,且B(﹣1,﹣2),C(3,1),则点A的坐标为 .
3.如图,在菱形ABCD中,直线MN分别交AB、CD、AC于点M、N和O.且AM=CN,连接BO.若∠OBC=60°,则∠DAC为( )
A.65° B.30° C.25° D.20°
4.如图,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE.
(1)求证:OE=CB;
(2)如果OC:OB=2:1,,求菱形的面积.
【类型二:菱形的判定】
5.在四边形ABCD中,AD=BC,AB=CD.下列说法能使四边形ABCD为菱形的是( )
A.AC=BD B.∠C=∠D C.∠A=∠B D.AC⊥BD
6.如图,四边形ABCD中,AC和BD是对角线,依据图中所标的数据,下列四边形不一定为菱形的是( )
A. B.
C. D.
7.一张矩形纸ABCD,将点B翻折到对角线AC上的点M处,折痕CE交AB于点E.将点D翻折到对角线AC上的点H处,折痕AF交DC于点F,折叠出四边形AECF.
(1)求证:AF∥CE;
(2)当∠BAC= 度时,四边形AECF是菱形?说明理由.
8.如图,四边形ABCD是平行四边形,O是对角线AC的中点,过点O的直线分别交边BC,AD于点E,F,连接AE,CF.
(1)求证:BE=DF;
(2)作∠AEB的平分线交AB于点G,若EG∥AC,求证:四边形AECF是菱形.
9.在 ABCD中,对角线AC与BD相交点O,过点O分别作AB和BC的垂线,垂足分别为H,M.
(1)如图1,当OH=OM时,求证:平行四边形ABCD是菱形;
(2)如图2,当∠ABC=90°时,若AB=OB,求的值.
【类型三:菱形的翻折问题】
10.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A.78° B.75° C.60° D.45°
11.如图,菱形纸片ABCD的边长为2,点E在边AB上,将纸片沿CE折叠,点B落在B′处,CB'⊥AD,垂足为F.若∠B=60°,则BE的长是 .
【类型四:菱形的旋转问题】
12.如图,在平行四边形ABCD中,∠A=70°,将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1BC1D1,当C1D1首次经过顶点C时,旋转角∠ABA1=( )
A.30° B.40° C.45° D.60°
13.如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O.点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),DF长度的最小值为 .
【类型五:菱形的动点问题】
14.如图1,在菱形ABCD中,点P沿A﹣B﹣C方向从点A移动到点C,设点P的移动路程为x,线段AP的长为y,点P在运动过程中y与x的变化关系如图2所示,点P运动到BC边上时,当x=18,y的值最小为12,则a的值是 .
15.如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)DH= ;DM= ;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
【类型六:菱形在一次函数中的存在性问题】
16.已知,如图,O为坐标原点,在四边形OABC中,BC∥OA,BC=24,A(26,0),C(0,12),点D是OA的中点,动点P在线段BC上以每秒2个单位长度的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当P运动 秒,四边形PDAB是平行四边形.
(2)在直线CB上是否存在一点Q,使得以O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由.
17.如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒3个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,请直接写出所有满足条件的点N的坐标.
【类型七:与菱形有关的作图题】
18.(1)图1是在Rt△ABC中,∠B=90°,用直尺和圆规作矩形ABCD,作法是“以点A为圆心,BC长为半径画弧;以点C为圆心,AB长为半径画弧,两弧交于点D“,请判断所作的四边形ABCD是不是矩形,并说明理由.
(2)如图2,在矩形ABCD的边AB上任取一点E,O是AC中点,在BC、CD、DA上各找一点F、G、H,使得四边形EFGH是菱形.(要求:利用直尺和圆规,作出图形,保留作图痕迹)
19.如图,在矩形ABCD中,BD是对角线.
(1)在AD边上确定一点E,将△BED沿BD翻折后,点E的对应点F恰好落在BC边上;(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,连接BE、DF,判断四边形BEDF的形状.
20.在平行四边形ABCD中,E、F分别是线段AD、BC上的点,请用直尺和圆规作菱形ABFE.
要求:
(1)用两种不同方法,不写作图过程,保留作图痕迹;
(2)选择其中一种给出证明过程.
21.如图①,在 ABCD中,AB=5,BC=13,BC边上的高为4.求作菱形AEFG,使点E在边AD上,点F,G在边BC上.
小宁的作法1.如图②,在边AD上取一点E.
2.以点A为圆心,AE长为半径画弧,交BC于点G.
3.在BC上截取GF=AE,连接EF,则四边形AEFG为所求作的菱形.
(1)证明小宁所作的四边形AEFG是菱形.
(2)小宁进一步探索,发现可作出的菱形的个数随着点E的位置变化而变化.请你继续探索,直接写出菱形的个数及对应的AE的长的取值范围.
【类型八:菱形综合题】
22.邻边长分别为1,a(a>1)的平行四边形纸片,如图那样折一下,剪下一个边长等于1的菱形(称为第一次操作);再把剩下的平行四边形如图那样折一下,剪下一个边长等于此时平行四边形一边长的菱形(称为第二次操作);再把剩下的平行四边形如此反复操作下去.若在第三次操作后,剩下的平行四边形为菱形,则a的值 .
23.如图,E为菱形ABCD对角线AC上一点,直线DE交射线AB于点F,AD=10,AC=8.
(1)求此菱形的面积;
(2)当△BEF是直角三角形时,求AE的长.
参考答案
【类型一:菱形的性质】
1.
【分析】先由菱形的性质得到AD=AB=BC=6,AC⊥BD,AC=2OA,再证明△ABC是等边三角形,则AC=AB=6,进而得到OA=3,由三线合一定理得到∠OAP=30°,则可求出,利用勾股定理得到,则.
【解答】解:∵四边形ABCD是菱形,
∴AD=AB=BC=6,AC⊥BD,AC=2OA,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=6,
∴OA=3,
∵AF⊥BC,
∴∠OAP=30°,
∴,
在Rt△AOD中,由勾股定理得,
∴,
故选:C.
2.
【分析】过B作BM⊥DC于点M,与y轴交于点N,由勾股定理求出BC=5,再由菱形的性质得AB=BC=5,即可解决问题.
【解答】解:如图,过B作BM⊥DC于点M,与y轴交于点N,
∵B(﹣1,﹣2),C(3,1),
∴BN=1,BF=EM=2,MN=3,CE=1,
∴BM=MN+BN=3+1=4,CM=CE+EM=1+2=3,
∵四边形ABCD是菱形,
∴AB=BC,
在Rt△BCM中,由勾股定理得:BC5,
∴AB=BC=5,
∴AF=AB﹣BF=5﹣2=3,
∵AB∥y轴,
∴点A的坐标为(﹣1,3),
故答案为:(﹣1,3).
3.
【分析】先由菱形性质得出AB∥CD,BC∥AD,BA=BC.结合AM=CN,证明△OAM≌△OCN(ASA),则OA=OC,因为∠OBC=60°,所以运用三角形内角和性质来计算,即可作答.
【解答】解:∵四边形ABCD是菱形,
∴AB∥CD,BC∥AD,BA=BC.
∴∠OMA=∠ONC,∠OAM=∠OCN,∠DAC=∠OCB.
在△OAM和△OCN中,
,
∴△OAM≌△OCN(ASA).
∴OA=OC.
∴BO⊥AC.
∴∠BOC=90°.
∵∠OBC=60°,
∴∠OCB=180°﹣∠BOC﹣∠OBC=30°.
∴∠DAC=∠OCB=30°.
故选:B.
4.(1)证明:点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,
∴AC⊥BD,四边形OCEB是平行四边形,∠COB=90°,
∴四边形OCEB是矩形,
∴OE=CB;
(2)解:∵四边形ABCD是菱形,OC:OB=2:1,,
∴,OC=2OB,
由(1)知,AC⊥BD,
在Rt△BOC中,由勾股定理得BC2=OC2+OB2,
即5=OC2+(2OC)2,
∴CO=2,OB=1.
∵四边形ABCD是菱形,
∴AC=4,BD=2,
∴菱形ABCD的面积.
【类型二:菱形的判定】
5.
【分析】先证四边形ABCD是平行四边形,再由菱形的判定和矩形的判定分别对各个选项进行判断即可.
【解答】解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
A、∵AC=BD,
∴平行四边形ABCD为矩形,故选项A不符合题意;
B、由AB=CD,不能判定四边形ABCD为菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠B,
∴∠A=∠B=90°,
∴平行四边形ABCD是矩形,故选项C不符合题意;
D、∵AC⊥BD,
∴平行四边形ABCD为菱形,故选项D符合题意;
故选:D.
6.
【分析】AC与BD交于点O,由OC=OA=3,OB=OD=4,可证明四边形ABCD是平行四边形,由OB2+OC2=BC2=25,证明∠BOC=90°,则四边形ABCD是菱形,可判断A不符合题意;由AB=AD=CB=CD=5,可证明四边形ABCD是菱形,可判断B不符合题意;由AD∥BC,AD=BC=5,证明四边形ABCD是平行四边形,由∠ADB=∠ABD=30°,得AB=AD,则四边形ABCD是菱形,可判断C不符合题意;若AB∥CD,则四边形ABCD是菱形;C′D与AB不平行,则四边形ABC′D不是菱形,可判断D符合题意,于是得到问题的答案.
【解答】解:如图1,AC与BD交于点O,
∵OC=OA=3,OB=OD=4,
∴四边形ABCD是平行四边形,
∵BC=5,
∴OB2+OC2=42+32=25,BC2=52=25,
∴OB2+OC2=BC2,
∴△BOC是直角三角形,且∠BOC=90°,
∴AC⊥BD,
∴四边形ABCD是菱形,
故A不符合题意;
如图2,∵AB=AD=CB=CD=5,
∴四边形ABCD是菱形,
故B不符合题意;
如图3,∵∠ADB=∠CBD=30°,
∴AD∥BC,
∵AD=BC=5,
∴四边形ABCD是平行四边形,
∵∠ADB=∠ABD=30°,
∴AB=AD,
∴四边形ABCD是菱形,
故C不符合题意;
若AB∥CD,
∵AB=CD=5,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形;
若C′D=AB=5,但C′D与AB不平行,则四边形ABC′D不是菱形,
∴四边形ABCD不一定是菱形,
故D符合题意,
故选:D.
7.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DAC=∠BCA,
由翻折知,∠DAF=∠HAF∠DAC,∠BCE=∠MCE∠BCA,
∴∠HAF=∠MCE,
∴AF∥CE;
(2)解:当∠BAC=30°时四边形AECF为菱形,理由如下:
∵四边形ABCD是矩形,
∴∠D=∠BAD=90°,AB∥CD,
由(1)得:AF∥CE,
∴四边形AECF是平行四边形,
∵∠BAC=30°,
∴∠DAC=60°.
∴∠ACD=30°,
由折叠的性质得∠DAF=∠HAF=30°,
∴∠HAF=∠ACD,
∴AF=CF,
∴四边形AECF是菱形;
故答案为:30.
8.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,AD=BC,
∴∠FAO=∠ECO,
在△FAO与△CEO中,
,
∴△FAO≌△CEO(ASA),
∴AF=CE,
∴AD﹣AF=BC﹣CE,
即BE=DF;
(2)∵AF=CE,AF∥CE,
∴四边形AECF是平行四边形,
∵EG∥AC,
∴∠GEB=∠ACE,∠GEA=∠EAC,
∵∠AEB的平分线交AB于点G,
∴∠GEB=∠GEA,
∴∠ACE=∠EAC,
∴AE=EC,
∴ AECF是菱形.
9.(1)证明:∵OH⊥AB,OM⊥BC,OH=OM,
∴∠ABD=∠CBD,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴OA=OC,OB=OD,BD=AC,
∴OA=OC=OB=OD,
∵AB=OB,
∴△ABC是等边三角形,
∴∠ABO=60°,
∴∠OBM=30°,
∵OH⊥AB,OM⊥BC,
∴四边形OHBM是矩形,
∴OH=BM,OB=2OM,
∴BMOM,
∴.
【类型三:菱形的翻折问题】
10.
【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.
【解答】解:连接BD,
∵四边形ABCD为菱形,∠A=60°,
∴△ABD为等边三角形,∠ADC=120°,∠C=60°,
∵P为AB的中点,
∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,
∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.
故选:B.
11.
【分析】作EH⊥BC于点H,则∠BHE=∠CHE=90°,求出∠ECB=45°,得到EH=CH,在Rt△EBH中,用BE表示EH,BH,再利用BH+CH=BC列方程解出即可.
【解答】解:作EH⊥BC于点H,则∠BHE=∠CHE=90°,
由折叠得BC=B′C=2,∠BCE=∠B′CE,
∵四边形ABCD是菱形,
∴BC∥AD,DC=BC=2,∠B=∠D=60°,
∵CB′⊥AD于点F,
∴∠BCB′=∠CFD=90°,
∴∠BCE=∠B′CE∠BCB′90°=45°,
∵∠B=60°,
∴∠DCF=30°,
∴DFDC2=1,
∴∠HEC=∠BCE=45°,
∴CH=EH,
在Rt△EBH中,
∵sinB,cosB,
∴CH=EHBE,BHBE,
∴BEBE=2,
∴BE,
故答案为:.
【类型四:菱形的旋转问题】
12.
【分析】根据平行四边形的性质及旋转的性质可知∠A=∠C=∠C1=70°,BC=BC1,然后可得∠BCC1=∠C1=70°,则有∠CBC1=40°,进而问题可求解.
【解答】解:∵四边形ABCD是平行四边形,∠A=70°,
∴∠A=∠C=70°,
由旋转的性质可得∠C=∠C1=70°,BC=BC1,∠ABA1=∠CBC1,
∴∠BCC1=∠C1=70°,
∴∠ABA1=∠CBC1=40°.
故选:B.
13.
【分析】连接BE,作BH⊥AD,由旋转的性质可得△DCF≌△BCE,把求DF的最小值转化为求BE的最小值,再根据垂线段最短可得答案.
【解答】解:连接BE,作BH⊥AD交DA的延长线于H,
菱形ABCD中,∠ABC=60°,
∴∠BCD=120°.
∵∠ECF=120°,
∴∠BCD=∠ECF,
∴∠BCE=∠DCF
由旋转可得:EC=FC,
在△BEC和△DFC中,
,
∴△DCF≌△BCE(SAS),
∴DF=BE,
即求DF的最小值转化为求BE的最小值.
∵在Rt△AHB中,∠BAH=60°,AB=2,
∴BH=2sin60°,
当E与H重合时,BE最小值是,
∴DF的最小值是.
故答案为:.
【类型五:菱形的动点问题】
14.
【分析】根据菱形的性质,再结合P运动时y随x的变化的关系图象,运用勾股定理即可求解.
【解答】解:如图1,过A点作AE⊥BC于E,
根据图2知:当点P与点E重合时,AB+BP=18,AP=12,
∴AB+BE=18,AE=12,
设AB=m,则BE=18﹣m,
在Rt△ABE中,AE2+BE2=AB2,
∴122+(18﹣m)2=m2,
解得:m=13,
∴AB=BC=CD=AD=13,BE=5,
∴EC=BC﹣BE=13﹣5=8,
当点P到达点C时,AP=AC=a,
在Rt△ACE中,AC2=AE2+EC2,即a2=122+82=208,
∵a>0,
∴a=4,
故答案为:4.
15.解:(1)在Rt△ADH中,AD=5,AH=3,
∴DH4,
在Rt△ADH中,AD=5,AH=3,
∴DH=4,
∵AC是菱形ABCD的对角线,
∴∠ACD=∠ACB,CD=CB,
在△DCM和△BCM中,
,
∴△DCM≌△BCM(SAS),
∴DM=BM,
在Rt△BHM中,BM=DM,HM=DH﹣DM=4﹣DM,BH=AB﹣AH=2,
根据勾股定理得,DM2﹣MH2=BH2,
即:DM2﹣(4﹣DM)2=4,
∴DM;
故答案为:4,;
(2)在△BCM和△DCM中,
,
∴△BCM≌△DCM(SAS),
∴BM=DM,∠CDM=∠CBM=90°
①当P在AB之间时,0<t,S(5﹣2t)t.
②当P在BC之间时,t<5,S(2t﹣5)t,
综上,S与t之间的函数关系式为S;
(3)存在,
∵∠ADM+∠BAD=90°,∠BCD=∠BAD,
∴∠ADM+∠BCD=90°,
∵∠MPB+∠BCD=90°,
∴∠MPB=∠ADM,
∵四边形ABCD是菱形,
∴∠DAM=∠BAM,
∵AM=AM,
∴△ADM≌△ABM(AAS),
∴∠ADM=∠ABM,
∴∠MPB=∠ABM,
∵MH⊥AB,
∴PH=BH=2,
∴BP=2BH=4,
∵AB=5,
∴AP=1,
∴t.
【类型六:菱形在一次函数中的存在性问题】
16.解:(1)∵A(26,0),C(0,12),
∴OA=26,OC=8,
∵点D时OA的中点,
∴OD=1OA=13,
由运动知,PC=2t,
∵BC=24,
∴BP=BC﹣PC=24﹣2t,
∵四边形PDAB是平行四边形,
∴PB=AD=13,
∴24﹣2t=13,
解得t=5.5,
∴当t值为5.5时,四边形PDAB是平行四边形.
故答案为:5.5;
(2)存在,分三种情况:
①当Q点在P点的右边时,如图,
∵四边形ODQP是菱形,
∴OD=OP=PQ=13,
∴在Rt△OPC中,由勾股定理得:PC=5,
∴2t=5,
解得t=2.5,
∴Q(18,12);
②当Q点在P点左侧且在BC线段上时,如图,
同理①得PC=18,
即2t=18,
解得t=9,
∴Q(5,12);
③当Q点在P点左侧且在BC延长线上时,如图3,
同理①求出QC=5,PC=13﹣5=8,
即2t=8,
解得t=4,
∴Q(﹣5,12);
综上,t=2.5时,Q(18,12),t=9时,Q(5,12),t=4时,Q(﹣5,12).
17.解:(1)若点P在点A的左侧,四边形PABQ为平行四边形,PA=QB,
由题意得4﹣3t=t,
解得t=1,
若点P在点A的右侧,四边形PAQB为平行四边形,PA=QB,
∴3t﹣4=t,
解得t=2,
综上:t=1或2时,以A,B,P,Q为顶点的四边形为平行四边形.
(2)N点坐标为(﹣5,3),(5,3),(0,﹣3),.
∵点A(4,0),C(0,3),
∴AO=4,OC=3,
∴AC5,
如图,以AC为边,四边形ACMN是菱形,
∵C(0,3),
∴N(0,﹣3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(5,3);
如图,以AC为边,四边形ACNM是菱形,
∵CN=AC=5,CN∥AM,
∴N(﹣5,3);
如图,以AC为对角线,四边形ACNM是菱形,
设CM=AM=CN=x,
∴OM=4﹣x,
∵OC2+OM2=CM2,
∴32+(4﹣x)2=x2,
∴,
∴CN,
∴N(,3);
综上所述,以A、C、M、N为顶点的四边形是菱形时,点N的坐标为(﹣5,3),(5,3),(0,﹣3),.
【类型七:与菱形有关的作图题】
18.解:(1)如图1中,四边形ABCD是矩形.
理由:∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=90°,
∴四边形ABCD是矩形;
(2)四边形EFGH即为所求.
19.解:(1)所作的图形如图:
;
(2)证明:四边形BEDF是菱形.理由如下:
∵四边形ABCD为矩形,
∴AD∥BC,
由翻折知,BE=BF,
由作图知,BE=DE,
∴DE=BF,
∴四边形BEDF是平行四边形,
∵BE=BF,
∴四边形BEDF是菱形.
20.解:(1)如图1、如图2,菱形ABFE为所作;
(2)如图1:∵四边形ABCD为平行四边形,
∴AD∥BC,
∵AE=AB,BF=AB,
∴AE=BF,
而AE∥BF,
∴四边形ABFE为平行四边形,
∵AB=AE,
∴四边形ABFE为菱形;
如图2:∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AEB=∠FBE,
∵BE平分ABC,
∴∠FBE=∠ABE,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得BF=BA,
由图1的结论得到四边形ABFE为菱形.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴AE∥GF,
∵AE=GF,
∴四边形AEFG是平行四边形,
∵AE=AG,
∴四边形AEFG是菱形.
(2)解:如图①中,过点A作AT⊥BC于点T,
在Rt△ABT中,BT3,
∵BC=13,
∴CT=13﹣3=10,
在TC上取一点G,使得AG=CG,设AG=CG=x,
则有x2=42+(10﹣x)2,
∴x,
观察图象可知:
①当0<AE<4时,菱形的个数为0;
②当AE=4时,菱形的个数为1;
③当4<AE≤5时,菱形的个数为2;
④当5<AE时,菱形的个数为1;
⑤当AE≤13时,菱形的个数为0.
【类型八:菱形综合题】
22.
【分析】根据题意,进行分类讨论,再根据菱形的性质,列出方程求解即可.
【解答】解:①如图,经历三次折叠后,四边形IJHF为菱形,
∵四边形ABCD为菱形,
∴AB=AD=BC=CD=1,
∴DF=CE=a﹣1,
∵四边形GCEH为菱形,
∴GC=CE=a﹣1,
∴DG=FH=1﹣(a﹣1)=2﹣a,
∵四边形DGJI为菱形,
∴DI=DG=2﹣a,
∴IF=a﹣1﹣(2﹣a)=2a﹣3,
∵四边形IJHF为菱形,
∴IF=HF,即2﹣a=2a﹣3,
解得:;
②如图,经历三次折叠后,四边形DIHF为菱形,
∵四边形ABCD为菱形,
∴AB=AD=BC=CD=1,
∴DF=CE=a﹣1,
∵四边形JCEG,IJGH,DIHF都为菱形,
∴,
∴,
解得:;
③如图,经历三次折叠后,四边形FIJH为菱形,
∵四边形ABCD,DCEF为菱形,
∴AB=AD=BC=CD=CE=DF=EF=1,
∴FH=a﹣2,
∵四边形FIJH,IEGJ都为菱形,
∴,
∴,
解得:;
④如图,经历三次折叠后,四边形HGIJ为菱形,
∵四边形ABCD,DCEF,FEGH,HGIJ都为菱形,
∴AB=AD=DF=FH=1,
∴HJ=a﹣3,
∴HJ=IJ,
∴a﹣3=1,
解得:a=4;
综上:a的值为或4或或.
23.解:(1)连接BD,交AC于点O,
∵四边形ABCD是菱形,
∴BO=DO,AOAC=4,AC⊥BD,
∴OD2,
∴BD=4,
∴菱形的面积 8 480;
(2)①当∠EFB=90°时,如图1,
∵∠EFB=90°,
∴菱形的面积=10 DF=80,
∴DF=8,
∴AF6,
∴BF=4,
∵AC垂直平分BD,
∴DE=BE,
∵BE2=FE2+BF2,
∴EF2+42=(8﹣EF)2,
得EF=3,
在△AEF中,AE3,
②当∠BEF=90°时,如图2,连接BD交AC于O,当点E在AO上时,
则△EDB是等腰直角三角形,BD=4,
∴OE=2,
∴AE=2;
当点E在OC上时,同理可求AE=6,
③当∠FBE=90°时,如图3,
∵AE2=BE2+AB2,AE OB=BA BE,
∴AE2=BE2+100,2AE=10BE,
∴AE2=(AE)2+100,
∴AE=5,
综上:AE的长为3或2或6或5.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
