2.1 折扣 (课件)(共23张PPT)人教版数学六年级下册
文档属性
| 名称 | 2.1 折扣 (课件)(共23张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 06:24:26 | ||
图片预览







文档简介
(共23张PPT)
第1课时 折扣
② 百分数(二)
人教版六年级数学下册
学习目标
1.结合具体情境,理解“打折”的含义。
2.能利用折扣和百分数之间的关系,解决折扣问题,提高解决问题的能力。
3.体会折扣在现实生活中的应用价值,懂得数学与生活的密切联系,增强学习数学的兴趣和信心。
课堂导入
12元/瓶
甲超市:买四送一
乙超市:八五折
我要买5瓶油。
同学们,张叔叔在哪家超市买合算呢?
商店有时会采用打折扣销售的方式,降价出售商品,俗称“打折”。几折就表示十分之几,也就是百分之几十。例如,打九折出售,就是按原价的90%出售。
(教科书第8页)
新知探究
280×_____=____(元)
(教科书第8页例1)
爸爸给小雨买了一辆自行车,原价280元,现在打八五折出售。买这辆自行车用了多少钱?
(1)
理解题意,抓住关键句。
1
85%
85%
打八五折出售
现在商品的价格是原价的85%
原来商品的价格是单位“1”
接下来用图示表示数量关系。
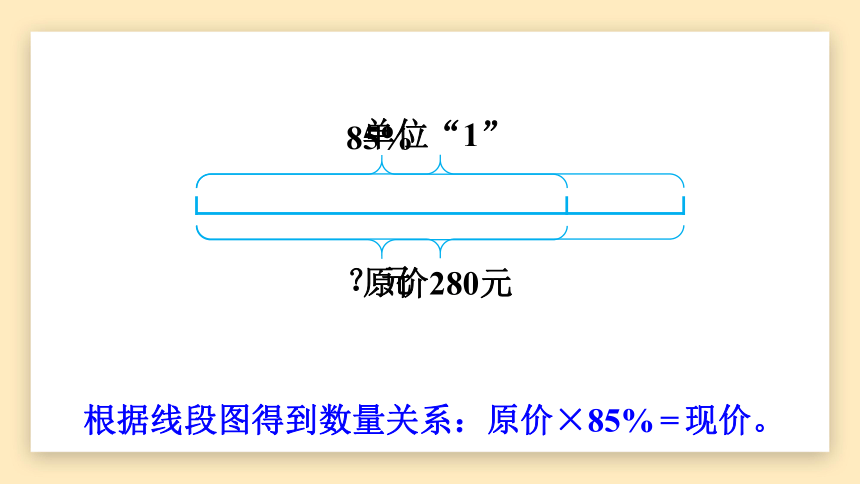
单位“1”
85%
原价280元
?元
根据线段图得到数量关系:原价×85%=现价。
爸爸给小雨买了一辆自行车,原价280元,现在打八五折出售。买这辆自行车用了多少钱?
(1)
1
280×85%=238 (元)
答:买这辆自行车用了238元钱。
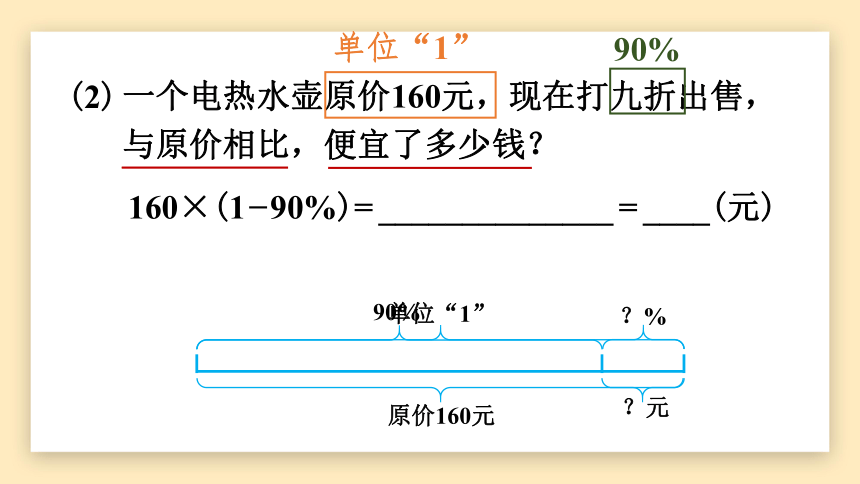
一个电热水壶原价160元,现在打九折出售,与原价相比,便宜了多少钱?
(2)
160×(1 90%)=______________=____(元)
单位“1”
90%
单位“1”
90%
原价160元
?%
?元
一个电热水壶原价160元,现在打九折出售,与原价相比,便宜了多少钱?
(2)
160×(1 90%)=______________=____(元)
根据线段图得到数量关系:
原价 现价=便宜的价钱;
原价×便宜的百分率=便宜的价钱。
160×10%
16
160 160×90%=160 144=16(元)
一件商品,按比进价高40%的价格出售,后来因为季节原因又打七折出售,降价后每件商品卖147元,现在卖出一件这种商品是赔还是赚?
实际是求进价是大于147元还是小于147元。
画图分析
>
把一件商品的进价看做单位“1”。
进价
进价的40%
原价
设一件商品的进价为x,则上图可用下面的等式来表示:
原价=x+40%x
画图分析
>
把一件商品的原价看做单位“1”。
原价的70%
原价
设一件商品的原价为y,则上图可用下面的等式来表示:
70%y=147
现价:147元
画图分析
>
把一件商品的进价看做单位“1”。
进价
进价的40%
原价
设一件商品的进价为x,则上图可用下面的等式来表示:
原价=x+40%x
y=x+40%x
(x+40%)70%=147
画图分析
>
把一件商品的原价看做单位“1”。
原价
设一件商品的原价为y,则上图可用下面的等式来表示:
现价:147元
70%y=147
规范答
>
设每件商品的进价是x元。
(x+40%)70%=147
1.4x×0.7=147
0.98x=147
x=150
147<150
答:现在卖出一件这种商品赔了。
算出下面各物品打折后的价钱。(单位:元)
现价:
原价:80.00
原价:105.00
原价:35.00
现价:
现价:
原价×折扣=现价
52.00
73.50
30.80
【教材P8 做一做】
随堂练习
2. (1)打折后,每种面包各多少元?
4×50%=2(元)
8.8×50%=4.4(元)
6×50%=3(元)
5×50%=2.5(元)
(2)晚8:00以后,玲玲拿了10元去买面包,她可以怎样买?
答案不唯一,合理即可。如:她可以买4个标价为5元的面包。
【教材P13 练习二 第1题】
3. 晓风的爸爸妈妈去买新家具,他们选中了图中
的4种家具。打折后, 4种家具分别应付多少钱?
220×80%=176(元)
120×80%=96(元)
2400×80%=1920(元)
880×80%=704(元)
【教材P13 练习二 第2题】
4. 书店的图书凭优惠卡购买可打八折,小明用优惠卡买了一套书,省了9.6元。这套书原价多少钱?
原价×(1-折扣)=节省的钱
9.6÷(1-80%)=48(元)
答:这套书原价是48元。
【教材P13 练习二 第3题】
课后小结
折扣问题的基本数量关系
现价=原价×折扣
折扣=现价÷原价
便宜的钱数=原价-原价×折扣
=原价×(1-折扣)
原价=现价÷折扣
第1课时 折扣
② 百分数(二)
人教版六年级数学下册
第1课时 折扣
② 百分数(二)
人教版六年级数学下册
学习目标
1.结合具体情境,理解“打折”的含义。
2.能利用折扣和百分数之间的关系,解决折扣问题,提高解决问题的能力。
3.体会折扣在现实生活中的应用价值,懂得数学与生活的密切联系,增强学习数学的兴趣和信心。
课堂导入
12元/瓶
甲超市:买四送一
乙超市:八五折
我要买5瓶油。
同学们,张叔叔在哪家超市买合算呢?
商店有时会采用打折扣销售的方式,降价出售商品,俗称“打折”。几折就表示十分之几,也就是百分之几十。例如,打九折出售,就是按原价的90%出售。
(教科书第8页)
新知探究
280×_____=____(元)
(教科书第8页例1)
爸爸给小雨买了一辆自行车,原价280元,现在打八五折出售。买这辆自行车用了多少钱?
(1)
理解题意,抓住关键句。
1
85%
85%
打八五折出售
现在商品的价格是原价的85%
原来商品的价格是单位“1”
接下来用图示表示数量关系。
单位“1”
85%
原价280元
?元
根据线段图得到数量关系:原价×85%=现价。
爸爸给小雨买了一辆自行车,原价280元,现在打八五折出售。买这辆自行车用了多少钱?
(1)
1
280×85%=238 (元)
答:买这辆自行车用了238元钱。
一个电热水壶原价160元,现在打九折出售,与原价相比,便宜了多少钱?
(2)
160×(1 90%)=______________=____(元)
单位“1”
90%
单位“1”
90%
原价160元
?%
?元
一个电热水壶原价160元,现在打九折出售,与原价相比,便宜了多少钱?
(2)
160×(1 90%)=______________=____(元)
根据线段图得到数量关系:
原价 现价=便宜的价钱;
原价×便宜的百分率=便宜的价钱。
160×10%
16
160 160×90%=160 144=16(元)
一件商品,按比进价高40%的价格出售,后来因为季节原因又打七折出售,降价后每件商品卖147元,现在卖出一件这种商品是赔还是赚?
实际是求进价是大于147元还是小于147元。
画图分析
>
把一件商品的进价看做单位“1”。
进价
进价的40%
原价
设一件商品的进价为x,则上图可用下面的等式来表示:
原价=x+40%x
画图分析
>
把一件商品的原价看做单位“1”。
原价的70%
原价
设一件商品的原价为y,则上图可用下面的等式来表示:
70%y=147
现价:147元
画图分析
>
把一件商品的进价看做单位“1”。
进价
进价的40%
原价
设一件商品的进价为x,则上图可用下面的等式来表示:
原价=x+40%x
y=x+40%x
(x+40%)70%=147
画图分析
>
把一件商品的原价看做单位“1”。
原价
设一件商品的原价为y,则上图可用下面的等式来表示:
现价:147元
70%y=147
规范答
>
设每件商品的进价是x元。
(x+40%)70%=147
1.4x×0.7=147
0.98x=147
x=150
147<150
答:现在卖出一件这种商品赔了。
算出下面各物品打折后的价钱。(单位:元)
现价:
原价:80.00
原价:105.00
原价:35.00
现价:
现价:
原价×折扣=现价
52.00
73.50
30.80
【教材P8 做一做】
随堂练习
2. (1)打折后,每种面包各多少元?
4×50%=2(元)
8.8×50%=4.4(元)
6×50%=3(元)
5×50%=2.5(元)
(2)晚8:00以后,玲玲拿了10元去买面包,她可以怎样买?
答案不唯一,合理即可。如:她可以买4个标价为5元的面包。
【教材P13 练习二 第1题】
3. 晓风的爸爸妈妈去买新家具,他们选中了图中
的4种家具。打折后, 4种家具分别应付多少钱?
220×80%=176(元)
120×80%=96(元)
2400×80%=1920(元)
880×80%=704(元)
【教材P13 练习二 第2题】
4. 书店的图书凭优惠卡购买可打八折,小明用优惠卡买了一套书,省了9.6元。这套书原价多少钱?
原价×(1-折扣)=节省的钱
9.6÷(1-80%)=48(元)
答:这套书原价是48元。
【教材P13 练习二 第3题】
课后小结
折扣问题的基本数量关系
现价=原价×折扣
折扣=现价÷原价
便宜的钱数=原价-原价×折扣
=原价×(1-折扣)
原价=现价÷折扣
第1课时 折扣
② 百分数(二)
人教版六年级数学下册
