3.1.3 圆柱的表面积 (课件)(共19张PPT)人教版数学六年级下册
文档属性
| 名称 | 3.1.3 圆柱的表面积 (课件)(共19张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 06:29:43 | ||
图片预览


文档简介
(共19张PPT)
第3课时 圆柱的表面积
③ 圆柱与圆锥
人教版六年级数学下册
学习目标
1.理解圆柱侧面积和表面积的意义。
2.通过观察思考、交流讨论推导并掌握求圆柱的侧面积和表面积的方法。
3.体验成功与失败的收获,体会合作的愉悦。
新课导入
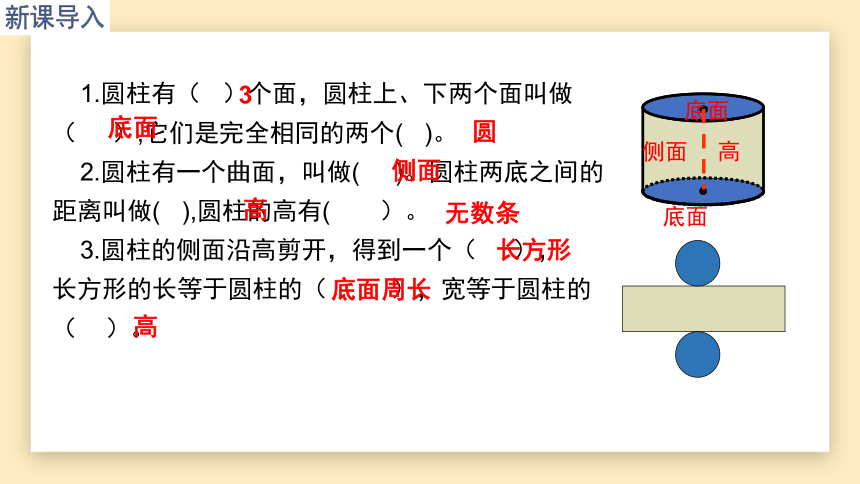
1.圆柱有( )个面,圆柱上、下两个面叫做( ),它们是完全相同的两个( )。
2.圆柱有一个曲面,叫做( )。圆柱两底之间的距离叫做( ),圆柱的高有( )。
3.圆柱的侧面沿高剪开,得到一个( ),
长方形的长等于圆柱的( ),宽等于圆柱的( )。
底面
底面
侧面
高
底面
侧面
无数条
3
圆
高
长方形
底面周长
高
新知探究
(教科书第20页例3)
3
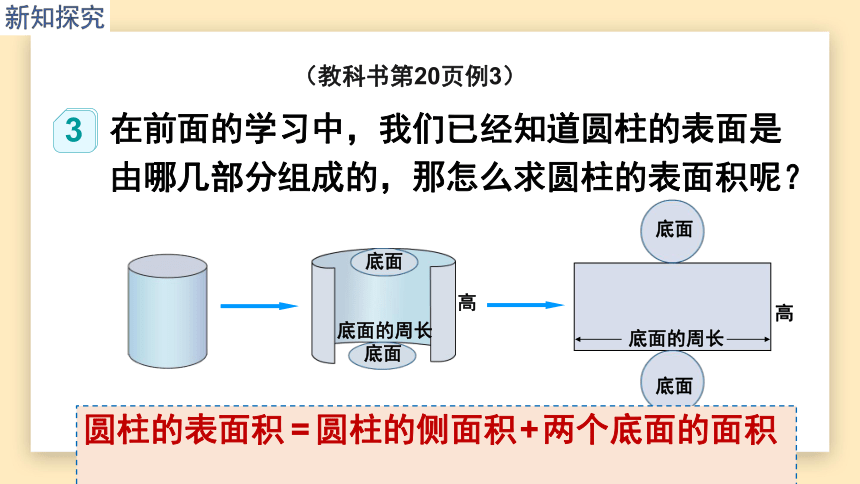
在前面的学习中,我们已经知道圆柱的表面是由哪几部分组成的,那怎么求圆柱的表面积呢?
底面
底面
高
底面的周长
底面
底面的周长
高
底面
观察上图,你能发现什么?
圆柱的表面积=圆柱的侧面积+两个底面的面积
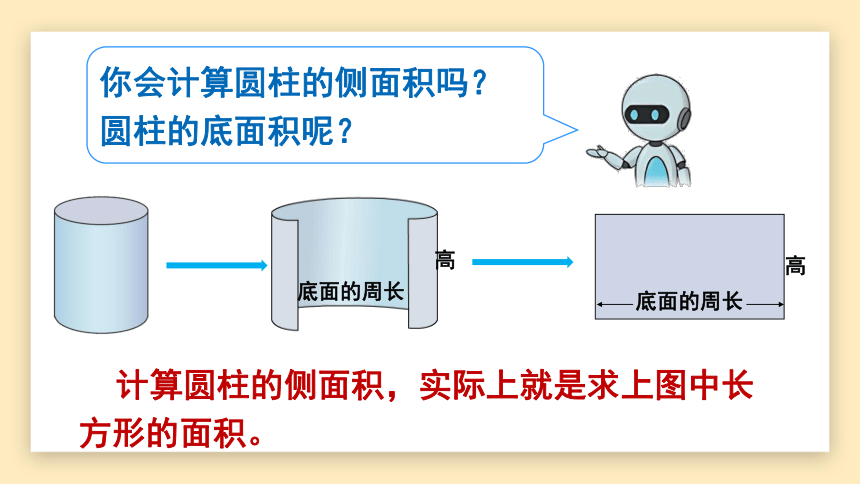
你会计算圆柱的侧面积吗?
圆柱的底面积呢?
计算圆柱的侧面积,实际上就是求上图中长
方形的面积。
底面的周长
高
高
底面的周长
底面的周长
高
高
底面的周长
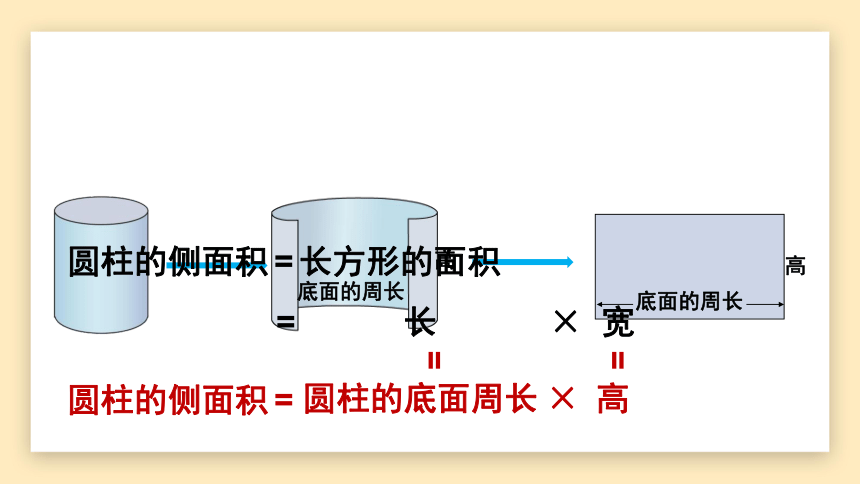
圆柱的侧面积=长方形的面积
= 长 × 宽
圆柱的底面周长
=
高
=
×
圆柱的侧面积=
底面的周长
高
高
底面的周长
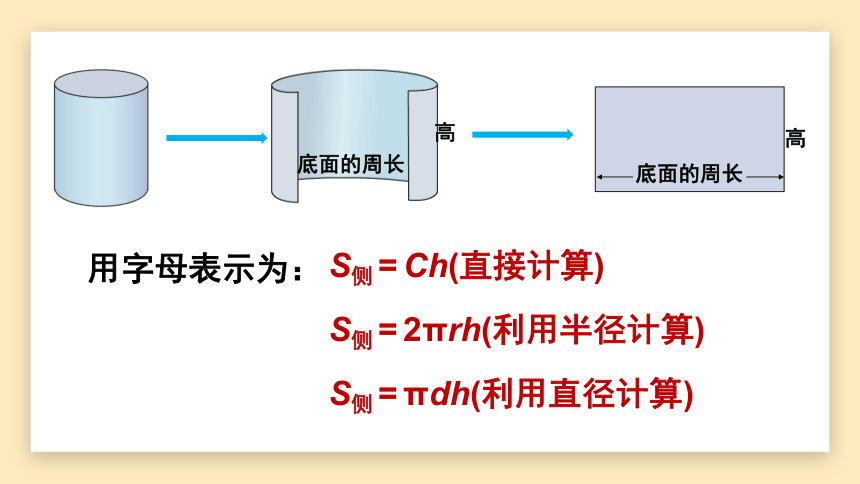
用字母表示为:
S侧=Ch(直接计算)
S侧=2πrh(利用半径计算)
S侧=πdh(利用直径计算)
圆柱的表面积=圆柱的侧面积+两个底面的面积
两个圆的面积
2πr2
=
S表=2πrh+2πr2 (利用半径计算)
一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)
求大约要用多少面料,就是求……
(教科书第21页例4)
4
一顶厨师帽近似圆柱形的表面积
帽子的侧面积+帽顶的面积
=
帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子大约要用2200cm2的面料。
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
在取近似值时,个位上的数即使是4或者比4小的数,也要向前一位进1,这种取近似值的方法叫做“进一法”。
随堂练习
教材第21页“做一做”第1题
1.求下面各圆柱的侧面积。
(1)底面周长是1.6 m,高是0.7 m。
1.6×0.7=1.12( m2 )
答:圆柱的侧面积是1.12 m2 。
(2)底面半径是3.2 dm,高是5 dm。
2×3.14×3.2 ×5=100.48(dm2 )
答:圆柱的侧面积是100.48 dm2。
S侧=Ch
S侧=2πrh
答:这张商标纸的面积是314 cm2。
2.一个圆柱形罐头的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
2×3.14×5×10=314(cm2)
S侧=2πrh
教材第20页“做一做”
3.计算下面图形的表面积。
C=31.4 cm
h=8 cm
高10 dm
直径
3 dm
(1)S表=Ch+2π(C÷2π)2
=251.2+157
31.4×8+2×3.14×(31.4÷2÷3.14)
=408.2(cm )
(1)
(2)
3.计算下面图形的表面积。
C=31.4 cm
h=8 cm
高10 dm
直径
3 dm
(2)S表=πdh+2π(d÷2)2
= 94.2+14.13
3.14×3×10 + 2×3.14×(3÷2)
=108.33(dm )
(1)
(2)
4.小亚做了一个笔筒,她想给笔筒的外侧面和外底面贴上彩纸,大约需要用多少彩纸?(得数保留整十数。)
8 cm
13 cm
(1)侧面积:3.14×8×13=326.56(cm2 )
(2)一个底面的面积:3.14×(8÷2) =50.24(cm2 )
(3)大约需要用的彩纸:326.56+50.24=376.8(cm2 )
答:大约需要用380 cm2的彩纸。
笔筒只需计算侧面积和1个底面积。
教材第21页“做一做”第2题
376.8 cm2≈ 380 cm2
5.一个刷油漆的滚筒(如图所示)长为1.4 dm,直径为5 cm。如果它向一个方向滚动100周,能刷墙多少平方分米?
滚筒滚一周刷墙面积:S=πdh
3.14×0.5×1.4×100=219.8(dm2 )
5 cm=0.5 dm
答:能刷墙219.8 dm2。
课堂小结
回顾本节课,你学会了什么?
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
第3课时 圆柱的表面积
③ 圆柱与圆锥
人教版六年级数学下册
第3课时 圆柱的表面积
③ 圆柱与圆锥
人教版六年级数学下册
学习目标
1.理解圆柱侧面积和表面积的意义。
2.通过观察思考、交流讨论推导并掌握求圆柱的侧面积和表面积的方法。
3.体验成功与失败的收获,体会合作的愉悦。
新课导入
1.圆柱有( )个面,圆柱上、下两个面叫做( ),它们是完全相同的两个( )。
2.圆柱有一个曲面,叫做( )。圆柱两底之间的距离叫做( ),圆柱的高有( )。
3.圆柱的侧面沿高剪开,得到一个( ),
长方形的长等于圆柱的( ),宽等于圆柱的( )。
底面
底面
侧面
高
底面
侧面
无数条
3
圆
高
长方形
底面周长
高
新知探究
(教科书第20页例3)
3
在前面的学习中,我们已经知道圆柱的表面是由哪几部分组成的,那怎么求圆柱的表面积呢?
底面
底面
高
底面的周长
底面
底面的周长
高
底面
观察上图,你能发现什么?
圆柱的表面积=圆柱的侧面积+两个底面的面积
你会计算圆柱的侧面积吗?
圆柱的底面积呢?
计算圆柱的侧面积,实际上就是求上图中长
方形的面积。
底面的周长
高
高
底面的周长
底面的周长
高
高
底面的周长
圆柱的侧面积=长方形的面积
= 长 × 宽
圆柱的底面周长
=
高
=
×
圆柱的侧面积=
底面的周长
高
高
底面的周长
用字母表示为:
S侧=Ch(直接计算)
S侧=2πrh(利用半径计算)
S侧=πdh(利用直径计算)
圆柱的表面积=圆柱的侧面积+两个底面的面积
两个圆的面积
2πr2
=
S表=2πrh+2πr2 (利用半径计算)
一顶厨师帽近似圆柱形,高30cm,帽顶直径20cm,做这样一顶帽子大约要用多少平方厘米的面料?(得数保留整十数。)
求大约要用多少面料,就是求……
(教科书第21页例4)
4
一顶厨师帽近似圆柱形的表面积
帽子的侧面积+帽顶的面积
=
帽子的侧面积:3.14×20×30=1884(cm2)
帽顶的面积:3.14×(20÷2)2=314(cm2)
需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子大约要用2200cm2的面料。
实际使用的面料要比计算的结果多一些,所以这类问题往往用“进一法”取近似数。
在取近似值时,个位上的数即使是4或者比4小的数,也要向前一位进1,这种取近似值的方法叫做“进一法”。
随堂练习
教材第21页“做一做”第1题
1.求下面各圆柱的侧面积。
(1)底面周长是1.6 m,高是0.7 m。
1.6×0.7=1.12( m2 )
答:圆柱的侧面积是1.12 m2 。
(2)底面半径是3.2 dm,高是5 dm。
2×3.14×3.2 ×5=100.48(dm2 )
答:圆柱的侧面积是100.48 dm2。
S侧=Ch
S侧=2πrh
答:这张商标纸的面积是314 cm2。
2.一个圆柱形罐头的侧面贴着商标纸,圆柱底面半径是5 cm,高是10 cm。这张商标纸的面积是多少?
2×3.14×5×10=314(cm2)
S侧=2πrh
教材第20页“做一做”
3.计算下面图形的表面积。
C=31.4 cm
h=8 cm
高10 dm
直径
3 dm
(1)S表=Ch+2π(C÷2π)2
=251.2+157
31.4×8+2×3.14×(31.4÷2÷3.14)
=408.2(cm )
(1)
(2)
3.计算下面图形的表面积。
C=31.4 cm
h=8 cm
高10 dm
直径
3 dm
(2)S表=πdh+2π(d÷2)2
= 94.2+14.13
3.14×3×10 + 2×3.14×(3÷2)
=108.33(dm )
(1)
(2)
4.小亚做了一个笔筒,她想给笔筒的外侧面和外底面贴上彩纸,大约需要用多少彩纸?(得数保留整十数。)
8 cm
13 cm
(1)侧面积:3.14×8×13=326.56(cm2 )
(2)一个底面的面积:3.14×(8÷2) =50.24(cm2 )
(3)大约需要用的彩纸:326.56+50.24=376.8(cm2 )
答:大约需要用380 cm2的彩纸。
笔筒只需计算侧面积和1个底面积。
教材第21页“做一做”第2题
376.8 cm2≈ 380 cm2
5.一个刷油漆的滚筒(如图所示)长为1.4 dm,直径为5 cm。如果它向一个方向滚动100周,能刷墙多少平方分米?
滚筒滚一周刷墙面积:S=πdh
3.14×0.5×1.4×100=219.8(dm2 )
5 cm=0.5 dm
答:能刷墙219.8 dm2。
课堂小结
回顾本节课,你学会了什么?
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
第3课时 圆柱的表面积
③ 圆柱与圆锥
人教版六年级数学下册
