3.2.2 圆锥的体积 (课件)(共18张PPT)人教版数学六年级下册
文档属性
| 名称 | 3.2.2 圆锥的体积 (课件)(共18张PPT)人教版数学六年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第2课时 圆锥的体积
③ 圆柱与圆锥
人教版六年级数学下册
学习目标
1.掌握圆锥体积的计算方法,会用公式计算体积,解决简单的实际问题。
2.理解圆锥体积计算公式的推导过程,理解圆柱与圆锥的关系。
新课导入
建筑工地上常用铅锤来确定建筑物是否竖直。
观察下,它是一个什么形状的物体呢?
圆锥
一、新课引入
可以怎样测量这个圆锥形铅锤的体积呢?
排水法可以测量物体的体积,把铅锤放入盛有水的量杯里,观察水面上升的高度,就可以求出铅锤的体积。
那沙堆、小麦堆等能用排水法测量它们的体积吗?
沙堆
小麦堆
新知探究
我们会计算圆柱的体积,怎样计算圆锥的体积呢?
(教科书第32页例2)
2
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
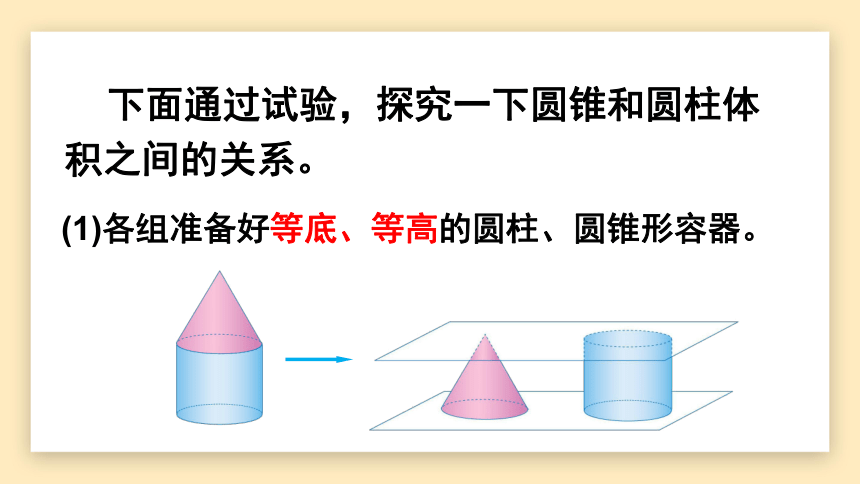
下面通过试验,探究一下圆锥和圆柱体
积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或倒水的方法试一试。
我把圆柱装满沙子,再往圆锥里倒。
圆锥装满后,我把沙子倒进盒子里,正好到了三次,
三次正好装满。
等高
(3)通过实验,你能发现圆锥的体积与同它等底、等
高的圆柱的体积之间的关系吗?
等底
(3)通过实验,你能发现圆锥的体积与同它等底、等
高的圆柱的体积之间的关系吗?
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子大约重1.5t,这堆沙子大约重多少吨?
(教科书第33页例3)
4m
1.5m
3
在利用公式算出沙堆的体积:
先求沙堆底面积:
6.28×1.5=9.42(t)
最后求出沙子的重量:
答:这堆沙子大约重9.42t。
3.14 ×(4÷2)2=3.14×4=12.56(m2)
随堂练习
1.填空。
(1)圆锥的体积等于和它( )的圆柱体积的( ),圆锥的体积计算公式可以写成( )。
等底、等高
(2)一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是( )立方米。
21.6
1
3
V圆锥= V圆柱= Sh
1
3
1
3
(2)圆锥的体积扩大到原来的3倍,它就变成了圆柱。( )
(1)圆柱的高是3 cm,与它等底、等体积的圆锥的高是9 cm。( )
×
√
(3)圆锥的体积是总是比圆柱的体积小。( )
×
2.判断。
3.一个圆锥形的零件,底面积是19 cm ,高是12 cm,这个零件的体积是多少?
答:这个零件的体积是76 cm3。
×19 ×12=76(cm )
V圆锥= Sh
教材第33页“做一做”第1题
4.如图,一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高是6 cm。每立方厘米钢大约重7.9 g。这个铅锤大约重多少克?(得数保留整数。)
(1)铅锤底面积:
3.14×(4÷2)2=12.56(cm2)
(2)铅锤的体积:
25.12×7.9≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198 g。
教材第33页“做一做”第2题
×12.56×6=25.12(cm3)
课堂小结
等底、等高
圆柱体积等于圆锥体积的3倍
圆锥体积等于圆柱体积的
第2课时 圆锥的体积
③ 圆柱与圆锥
人教版六年级数学下册
第2课时 圆锥的体积
③ 圆柱与圆锥
人教版六年级数学下册
学习目标
1.掌握圆锥体积的计算方法,会用公式计算体积,解决简单的实际问题。
2.理解圆锥体积计算公式的推导过程,理解圆柱与圆锥的关系。
新课导入
建筑工地上常用铅锤来确定建筑物是否竖直。
观察下,它是一个什么形状的物体呢?
圆锥
一、新课引入
可以怎样测量这个圆锥形铅锤的体积呢?
排水法可以测量物体的体积,把铅锤放入盛有水的量杯里,观察水面上升的高度,就可以求出铅锤的体积。
那沙堆、小麦堆等能用排水法测量它们的体积吗?
沙堆
小麦堆
新知探究
我们会计算圆柱的体积,怎样计算圆锥的体积呢?
(教科书第32页例2)
2
圆锥的体积和圆柱的体积有没有关系呢?
圆柱的底面是圆,圆锥的底面也是圆……
下面通过试验,探究一下圆锥和圆柱体
积之间的关系。
(1)各组准备好等底、等高的圆柱、圆锥形容器。
(2)用倒沙子或倒水的方法试一试。
我把圆柱装满沙子,再往圆锥里倒。
圆锥装满后,我把沙子倒进盒子里,正好到了三次,
三次正好装满。
等高
(3)通过实验,你能发现圆锥的体积与同它等底、等
高的圆柱的体积之间的关系吗?
等底
(3)通过实验,你能发现圆锥的体积与同它等底、等
高的圆柱的体积之间的关系吗?
工地上有一堆沙子,其形状近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子大约重1.5t,这堆沙子大约重多少吨?
(教科书第33页例3)
4m
1.5m
3
在利用公式算出沙堆的体积:
先求沙堆底面积:
6.28×1.5=9.42(t)
最后求出沙子的重量:
答:这堆沙子大约重9.42t。
3.14 ×(4÷2)2=3.14×4=12.56(m2)
随堂练习
1.填空。
(1)圆锥的体积等于和它( )的圆柱体积的( ),圆锥的体积计算公式可以写成( )。
等底、等高
(2)一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是( )立方米。
21.6
1
3
V圆锥= V圆柱= Sh
1
3
1
3
(2)圆锥的体积扩大到原来的3倍,它就变成了圆柱。( )
(1)圆柱的高是3 cm,与它等底、等体积的圆锥的高是9 cm。( )
×
√
(3)圆锥的体积是总是比圆柱的体积小。( )
×
2.判断。
3.一个圆锥形的零件,底面积是19 cm ,高是12 cm,这个零件的体积是多少?
答:这个零件的体积是76 cm3。
×19 ×12=76(cm )
V圆锥= Sh
教材第33页“做一做”第1题
4.如图,一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高是6 cm。每立方厘米钢大约重7.9 g。这个铅锤大约重多少克?(得数保留整数。)
(1)铅锤底面积:
3.14×(4÷2)2=12.56(cm2)
(2)铅锤的体积:
25.12×7.9≈198(g)
(3)铅锤的质量:
答:这个铅锤大约重198 g。
教材第33页“做一做”第2题
×12.56×6=25.12(cm3)
课堂小结
等底、等高
圆柱体积等于圆锥体积的3倍
圆锥体积等于圆柱体积的
第2课时 圆锥的体积
③ 圆柱与圆锥
人教版六年级数学下册
