函数的单调性与导数公开课课件

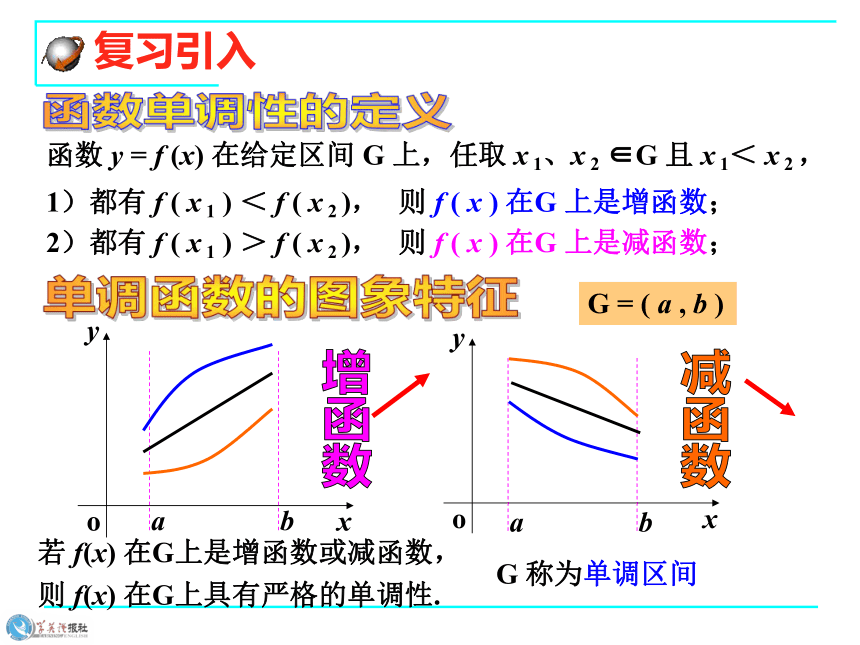
课件23张PPT。1.3.1函数的单调性与导数执教者： 涂海滨 同学们都知道，函数贯穿高中数学的始终，之前，我们学习了许多函数，那之前我们研究函数都研究哪些性质呢？ 情境引入思考 情境引入 函数的单调性（又叫增减性）是函数的一个重要性质，以前我们学习了函数单调性的判定一般有两种方法：定义法和图像法。函数 y = f (x) 在给定区间 G 上，任取 x 1、x 2 ∈G 且 x 1＜ x 2 ，函数单调性的定义单调函数的图象特征1）都有 f ( x 1 ) ＜ f ( x 2 )，则 f ( x ) 在G 上是增函数；2）都有 f ( x 1 ) ＞ f ( x 2 )，则 f ( x ) 在G 上是减函数；若 f(x) 在G上是增函数或减函数，增函数减函数则 f(x) 在G上具有严格的单调性.G 称为单调区间G = ( a , b ) 复习引入 复习引入思考 以前,我们用定义来判断函数的单调性.在假设x1f (x1)与f (x2) 的大小,在函数y= f (x)比较复杂的情况下,比较 f (x1)与 f (x2)的大小并不很容易.导数作为研究函数的一个重要工具，那能不能利用导数来判断函数的单调性呢？ 引入（4）对数函数的导数:（5）指数函数的导数: （3）三角函数 ： （1）常数函数：(C)/ ? 0 , (c为常数)； （2）幂函数 ： (xn)/ ? nxn?1 1. 基本初等函数的导数公式 复习回顾 2. 导数的运算法则（1）．函数的和或差的导数
(u±v)/＝u/±v/.（3）．函数的商的导数
（ ） / = (v≠0).
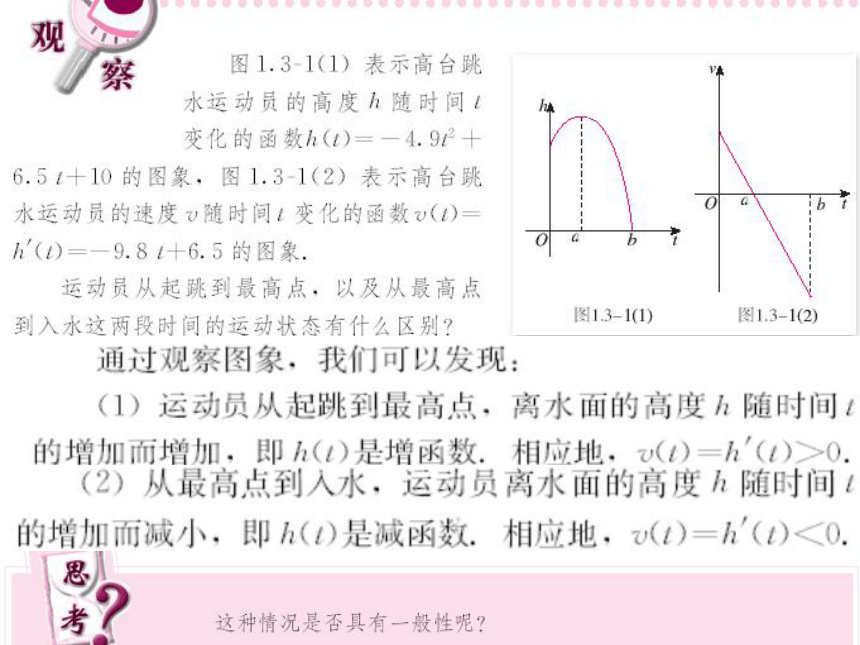
（2）．函数的积的导数 (uv)/＝u/v+uv/. 复习回顾 我们已经知道,曲线y=f (x)的切线的斜率就是函数y=f (x)的导数. 从函数y=x2-4x+3的图像可以看到: 在区间(2,+∞)内,切线的斜率为正,函数y=f (x)的值随着x的增大而增大,即 >0 时,函数y=f (x) 在区间(2, +∞)内为增函数. 在区间(-∞,2)内,切线的斜率为负,函数y= f (x)的值随着x的增大而减小,即 <0 时,函数y=f (x) 在区间(-∞,2)内为减函数. 新课f '(x)>0f '(x)<0由上我们可得以下的结论:如果在某个区间内恒有 ,则 为常数. 定义:一般地,设函数y=f (x)在某个区间（a，b）内有导数,如果在 这个区间内 >0,那么函数y=f (x) 在为这个区间内 的增函数;如果在这个区间内 <0,那么函数y=f (x) 在为这个区间内的减函数. 例题讲解①当1②当x>4,或x<1时， ;
③当x=4,或x=1时， .
试画出函数f(x)图象的大致形状.
CD判断下列函数的单调性, 并求出单调区间:例2你能小结求解函数单调区间的步骤吗？（2）求导数 ；（1）确定函数 的定义域；（3）解不等式 ，解集在定义域内的部分
为增区间； 解不等式 ，解集在定义域内的部分
为减区间．归纳总结1、判断下列函数的单调性, 并求出单调区间:练习：P 26小结1.本节课我们学习了什么？2.如何利用导数来求函数的单调区间？课本31页 A组1，2.课后作业谢谢指导！解: 2.求证: 函数 在 内是减函数. 由 , 解得 , 所以函数 的递减区间是 , 即函数 在 内是减函数.练习：P 263.讨论二次函数 的单调区间. 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是 由 , 得 , 即函数 的递增区间是 ; 相应地, 函数的递减区间是练习：P 26解: 4.函数 的图象如图所示, 试画出导函数 图象的大致形状练习：P 26