【期中押题卷】上海市2024-2025学年六年级下学期期中模拟预测数学试卷沪教版(含解析)
文档属性
| 名称 | 【期中押题卷】上海市2024-2025学年六年级下学期期中模拟预测数学试卷沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 08:45:54 | ||
图片预览




文档简介
上海市2024-2025学年六年级下学期期中模拟预测数学试卷
一.填空题(共10小题,满分20分,每小题2分)
1.(2分)同学们去看电影,小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的 边。
2.(2分)把一根长3米、底面直径是2分米的圆柱形钢材平均截成3个小圆柱,表面积增加了 平方分米。
3.(2分)(2022 永年区)把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是 立方分米。
4.(2分)三个内角的度数比为1:2:3的三角形,它是 三角形。
5.(2分)(2021春 渭滨区期中)一个圆柱和一个圆锥等底等高,它们的体积之和是48dm3,圆柱的体积是 dm3。
6.(2分)阳阳参加诗歌朗诵比赛,七名评委给他的评分分别是9.4分、9.2分、9.9分、9.3分、9.1分、9.7分、9.4分。
(1)这七名评委给阳阳打的平均分是 分。(结果保留两位小数)
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是 分。
7.(2分)(2023春 宜春期中)某校自来水管的内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手走时忘记关闭水龙头,3分钟浪费 升水。
8.(2分)(2022 怀安县)三角形的底一定,面积和高成 比例;三角形的面积一定,底和高成 比例。
9.(2分)(2022春 电白区期中)一个圆柱的底面直径扩大3倍,侧面积也扩大3倍。
10.(2分)(2020秋 兰考县期末)用 个相同的能拼成一个大的正方体。
二.判断题(共5小题,满分10分,每小题2分)
11.(2分)每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。
12.(2分)(2023 邢台模拟)50立方厘米比5平方厘米显然要大得多。
13.(2分)(2024 郾城区)把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是2:3。
14.(2分)(2024 神木市)如果将向东走40m记作+40m,那么向西走20m记作﹣20m。
15.(2分)明辨是非我会断。
(1)一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积不变。
(2)底面积相等的圆柱和圆锥,圆锥的体积一定小于圆柱的体积。
(3)圆柱的底面直径是2cm,高是6.28cm,它的侧面展开后是一个正方形。
(4)如果一个圆柱和一个圆锥的体积相等,那么它们的高的比是3:1。
(5)如果两个圆柱的体积相等,那么它们的侧面积也相等。
(6)圆柱的侧面积等于底面积乘以高。
三.选择题(共5小题,满分10分,每小题2分)
16.(2分)今年春节,某地下午2:00的气温是+4℃;到了晚上9:00,气温是﹣10℃。说明该地( )
A.晚上9:00气温比下午2:00下降了10℃
B.晚上9:00气温是10℃
C.晚上9:00气温比下午2:00的气温高
D.晚上9:00的气温比下午2:00下降了14℃
17.(2分)(2020 红花岗区)一个零件实际长度是3米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )
A.1:20 B.20:1 C.1:50
18.(2分)一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的( )
A.一半 B.2倍 C.4倍 D.8倍
19.(2分)在10、25、40这三个数中添上( )不能组成比例。
A.16 B.100 C. D.8
20.(2分)(2022 裕华区)—个圆柱的体积是36立方米,与它等底等高的圆锥的体积是( )立方米。
A.12 B.24 C.108
四.计算题(共5小题,满分25分)
21.(4分)(2021秋 中山市期末)涂色表示下面的分数,并计算。
22.(6分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
23.(9分)
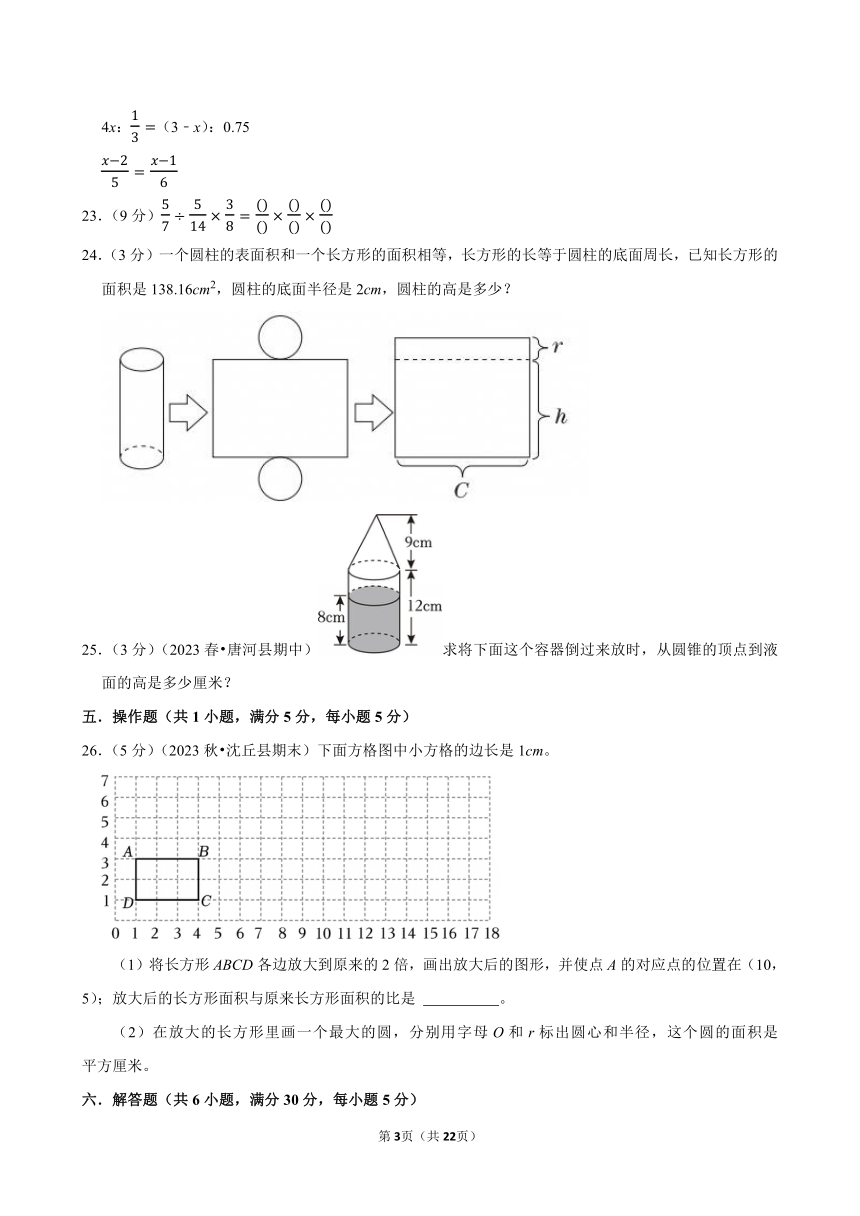
24.(3分)一个圆柱的表面积和一个长方形的面积相等,长方形的长等于圆柱的底面周长,已知长方形的面积是138.16cm2,圆柱的底面半径是2cm,圆柱的高是多少?
25.(3分)(2023春 唐河县期中)求将下面这个容器倒过来放时,从圆锥的顶点到液面的高是多少厘米?
五.操作题(共1小题,满分5分,每小题5分)
26.(5分)(2023秋 沈丘县期末)下面方格图中小方格的边长是1cm。
(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是 。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,这个圆的面积是 平方厘米。
六.解答题(共6小题,满分30分,每小题5分)
27.(5分)铺一间边长6米的正方形客厅,需用288块地砖。用同样的地砖铺边长9米的正方形客厅,需要多少块?(用比例解)
28.(5分)(2023 吉首市)一个圆锥形沙堆,底面积是56.52m2,高是3m。用这堆沙在10m宽的公路上铺3cm厚的路面,能铺多少米?
29.(5分)(2021 姜堰区)张村计划从村里修一条通往进城公路的最短水泥路(如图)。
(1)请你在图中画出这条最短的路线。
(2)量出这条最短的路线的图上距离,并标注在图上。(精确到毫米)
(3)这幅图的比例尺是1:30000,算出这条最短水泥路的实际距离是多少米?
30.(5分)(2022 息县)一个圆柱体水箱中水高为10厘米,圆柱的底面积为20平方厘米,现将一个石块放进水中(完全淹没),水溢出了30毫升。拿出石块,水面下降了4厘米,石块的体积是 立方厘米。
31.(5分)(2023 万源市)一堆水果,卖掉20%后,又卖掉了120千克,这时卖出的比剩下的多50%,这堆水果原来有多少千克?
32.(5分)(2022春 长兴县期中)如图,蜡烛每分钟燃烧的长度一定。(单位:cm)蜡烛最初的长度是多少厘米?
上海市2024-2025学年六年级下学期期中模拟预测数学试卷
参考答案与试题解析
一.填空题(共10小题,满分20分,每小题2分)
1.(2分)同学们去看电影,小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的 右 边。
【考点】位置.
【专题】应用意识.
【答案】右。
【分析】座位的顺序从左向右的顺序是:小丁丁、小巧、小亚,所以小亚在小丁丁的右边。
【解答】解:小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的右边。
故答案为:右。
【点评】本题考查位置,解决本题的关键是明确座位的顺序。
2.(2分)把一根长3米、底面直径是2分米的圆柱形钢材平均截成3个小圆柱,表面积增加了 12.56 平方分米。
【考点】圆柱的侧面积、表面积和体积.
【专题】运算能力.
【答案】12.56。
【分析】表面积增加部分就是指截取后增加的底面的面积;根据圆柱的截取方法可知,截成3个小圆柱,需要截取2次,那么增加了4个底面直径为2分米的圆柱的底面积,由此利用圆柱的底面积公式代入数据即可解决问题。
【解答】解:3.14×(2÷2)2×4
=3.14×1×4
=12.56(平方分米)
答:表面积增加了12.56平方分米。
故答案为:12.56。
【点评】正确找出增加的面是解决本题的关键。
3.(2分)(2022 永年区)把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是 56.52 立方分米。
【考点】圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】56.52。
【分析】这个圆锥的底面直径是6分米,高是6分米,再根据圆锥的体积=底面积×高÷3,解答即可。
【解答】解:3.14×(6÷2)2×6
3.14×9×6
=3.14×18
=56.52(立方分米)
答:这个圆锥的体积是56.52立方分米。
【点评】熟练掌握圆锥的体积公式,是解答此题的关键。
4.(2分)三个内角的度数比为1:2:3的三角形,它是 直角 三角形。
【考点】按比例分配应用题.
【专题】比和比例应用题;应用意识.
【答案】直角。
【分析】根据三角形的内角和是180°,把180°按1:2:3进行分配,求出最大角的度数,即可解答。
【解答】解:180°
=180°
=90°
答:它是直角三角形。
故答案为:直角。
【点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
5.(2分)(2021春 渭滨区期中)一个圆柱和一个圆锥等底等高,它们的体积之和是48dm3,圆柱的体积是 36 dm3。
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】36。
【分析】等底等高的圆柱的体积是圆锥的体积的3倍,把圆锥体积看作单位“1”,那么等底等高的圆柱和圆锥的体积之和是(1+3)倍,已知一个数的几倍是多少求这个数,用除法计算,由此即可解答。
【解答】解:48÷(1+3)
=48÷4
=12(dm3)
12×3=36(dm3)
答:圆柱的体积是36dm3。
故答案为:36。
【点评】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
6.(2分)阳阳参加诗歌朗诵比赛,七名评委给他的评分分别是9.4分、9.2分、9.9分、9.3分、9.1分、9.7分、9.4分。
(1)这七名评委给阳阳打的平均分是 9.43 分。(结果保留两位小数)
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是 9.4 分。
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题.
【答案】(1)9.43;(2)9.4。
【分析】对于(1),利用加法求出七位评委的总分,然后除以人数即可求出答案;
对于(2),去掉一个最高分、去掉一个最低分,用与(1)相同的方法解答。
【解答】解:(1)这七名评委给阳阳打的平均分是:
(9.4+9.2+9.9+9.3+9.1+9.7+9.4)÷7
=66÷7
≈9.43(分)
答:这七名评委给阳阳打的平均分是9.43分。
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是:
(9.4+9.2+9.3+9.7+9.4)÷5
=47÷5
=9.4(分)
答:阳阳的平均分是9.4分。
故答案为:9.43,9.4。
【点评】这是一道关于求平均数的题目,关键是掌握平均数的求法。
7.(2分)(2023春 宜春期中)某校自来水管的内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手走时忘记关闭水龙头,3分钟浪费 5.652 升水。
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】5.652。
【分析】分析题意,先求每秒流出的水的体积,即求直径是2cm,高是10cm的圆柱体积,用直径除以2,求出半径,将相关数据代入圆柱的体积公式即可求解;然后用每秒流出的水的体积乘以时间(注意单位的换算),即可求出3分钟流出的水的体积。
【解答】解:3分=180秒
3.14×(2÷2)2×10×180
=3.14×1800
=5652(立方厘米)
5652立方厘米=5.652升
答:3分钟浪费5.652升水。
故答案为:5.652。
【点评】本题主要考查圆柱体积的实际运用,关键是熟练掌握圆柱的体积公式。
8.(2分)(2022 怀安县)三角形的底一定,面积和高成 正 比例;三角形的面积一定,底和高成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:(1)因为三角形的面积=底×高÷2,
所以三角形的面积×2÷高=底(一定),
符合正比例的意义,
所以三角形的底一定,面积和高成正比例;
(2)因为三角形的面积=底×高÷2,
即底×高=长方形的面积×2(一定),
符合反比例的意义,
所以三角形形的面积一定,底和高成反比例。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
9.(2分)(2022春 电白区期中)一个圆柱的底面直径扩大3倍,侧面积也扩大3倍。 ×
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】因为圆柱的侧面积公式S=πdh可得,若高不变时,圆柱体的底面直径扩大3倍,它的侧面积就扩大3倍,据此解答。
【解答】解:圆柱的高不变,圆柱体的底面直径扩大3倍,它的侧面积就扩大3倍;但是本题没有说明高不变这个条件;
故答案为:×。
【点评】本题主要是利用圆柱的侧面积公式与积的变化规律解决问题。
10.(2分)(2020秋 兰考县期末)用 8 个相同的能拼成一个大的正方体。
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】8。
【分析】用小正方体拼组大正方体时,每个棱长上至少需要2个小正方体,由此即可解答。
【解答】解:用小正方体拼组大正方体时,每个棱长上至少需要2个小正方体,
所以拼成一个大正方体至少需要小正方体:2×2×2=8(个)
答:用8个相同的能拼成一个大的正方体。
故答案为:8。
【点评】抓住小正方体拼组大正方体的方法,是解决此类问题的关键。
二.判断题(共5小题,满分10分,每小题2分)
11.(2分)每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;推理能力.
【答案】√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。据此进行判断即可。
【解答】解:因为订餐的总钱数÷订餐的份数=每份快餐的单价(一定),因此每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(2分)(2023 邢台模拟)50立方厘米比5平方厘米显然要大得多。 ×
【考点】体积、容积及其单位.
【专题】综合判断题;应用意识.
【答案】×
【分析】立方厘米表示体积单位,平方厘米表示面积单位,无法比较。
【解答】解:立方厘米表示体积单位,平方厘米表示面积单位,无法比较。
50立方厘米比5平方厘米显然要大得多的说法错误。
故答案为:×。
【点评】本题考查的主要内容是体积单位的认识问题。
13.(2分)(2024 郾城区)把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是2:3。 √
【考点】圆锥的体积;圆柱的体积.
【专题】综合判断题;立体图形的认识与计算.
【答案】√
【分析】圆柱的体积是和它等底等高的圆锥体积的三倍,把圆柱削成最大的圆锥,则圆锥与圆柱等底等高,削去了两个圆锥的体积;也就是削去部分的体积是圆锥体积的2倍;据此判断。
【解答】解:圆柱体削成一个最大的圆锥体,
则:V圆柱=3V圆锥
(V圆柱﹣V圆锥):V圆柱
V圆柱:V圆柱
=2:3
答:削去部分的体积与圆柱的体积的比是2:3。
故题干的说法是正确。
故答案为:√。
【点评】此题考查等底等高的圆柱和圆锥体积间的关系。
14.(2分)(2024 神木市)如果将向东走40m记作+40m,那么向西走20m记作﹣20m。 √
【考点】负数的意义及其应用.
【专题】整数的认识;数感.
【答案】√
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,由此直接得出结论即可。
【解答】解:如果向东走600m记作+600m,那么向西走20m记作﹣20m,所以本题说法正确。
故答案为:√。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
15.(2分)明辨是非我会断。
(1)一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积不变。 ×
(2)底面积相等的圆柱和圆锥,圆锥的体积一定小于圆柱的体积。 ×
(3)圆柱的底面直径是2cm,高是6.28cm,它的侧面展开后是一个正方形。 √
(4)如果一个圆柱和一个圆锥的体积相等,那么它们的高的比是3:1。 ×
(5)如果两个圆柱的体积相等,那么它们的侧面积也相等。 ×
(6)圆柱的侧面积等于底面积乘以高。 ×
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】×,×,√,×,×,×
【分析】圆柱的体积=圆柱的底面积×高,圆柱的体积由圆柱的底面积和高两个因素共同决定的。
圆柱的侧面展开图是一个长方形,长是圆柱的底面周长,宽是圆柱的高。
若圆柱的底面周长=圆柱的高,则它的展开图是正方形。
【解答】解:1.一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积变为原来的,故原题说法错误;
2.底面积相等的圆柱和圆锥,没有给出高,无法判断圆锥的体积与圆柱的体积的大小,故原题说法错误;
3.圆柱的底面直径是2cm,则底面周长是3.14×2=6.28cm,高是6.28cm,它的侧面展开后是一个正方形,故原题说法正确;
4.如果一个圆柱和一个圆锥的体积相等,它们的高的比无法确定,故原题说法错误;
5.如果两个圆柱的体积相等,则底面积与高的乘积相等,侧面积的大小无法判断,故原题说法错误;
6.圆柱的侧面积等于底面周长乘以高,故原题说法错误。
故答案为:1.×;2.×;3. ;4.×;5.×;6.×。
【点评】本题是一道有关圆锥的体积、圆柱的体积的题目,解决本题的关键是利用公式计算即可。
三.选择题(共5小题,满分10分,每小题2分)
16.(2分)今年春节,某地下午2:00的气温是+4℃;到了晚上9:00,气温是﹣10℃。说明该地( )
A.晚上9:00气温比下午2:00下降了10℃
B.晚上9:00气温是10℃
C.晚上9:00气温比下午2:00的气温高
D.晚上9:00的气温比下午2:00下降了14℃
【考点】正、负数的运算.
【专题】数的运算.
【答案】D
【分析】用下午2:00的气温减去晚上9:00的气温即可。
【解答】解:4﹣(﹣10)
=4+10
=14(℃)
答:晚上9:00的气温比下午2:00下降了14℃。
故选:D。
【点评】根据正负数的运算方法,解答此题即可。
17.(2分)(2020 红花岗区)一个零件实际长度是3米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )
A.1:20 B.20:1 C.1:50
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】C
【分析】根据比例尺=图上距离:实际距离,代入数值计算即可。
【解答】解:6厘米:3米
=6:300
=1:50
答:这张图纸的比例尺是1:50。
故选:C。
【点评】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离:实际距离。
18.(2分)一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的( )
A.一半 B.2倍 C.4倍 D.8倍
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】B
【分析】长方体的体积与正方体的体积都等于底面积乘高,当长方体与正方体的体积相等时,它们的底面积与高的乘积相等;再根据长方体的高是正方体的高的一半,即可得出长方体底面积与正方体底面积的关系。
【解答】解:由分析可得:一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的2倍。
故选:B。
【点评】本题是一道关于长方体和正方体体积的题目,掌握体积计算公式是解题的关键。
19.(2分)在10、25、40这三个数中添上( )不能组成比例。
A.16 B.100 C. D.8
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】D
【分析】根据比例的基本性质内项之积等于外项之积,即可判断。
【解答】解:A.10×40=400
25×16=400
能组成比例。
B.25×40=1000
10×100=1000
能组成比例。
C.40250
10×25=250
能组成比例。
D.10×25=250
40×8=320
不能组成比例。
故选:D。
【点评】本题考查的是比例的基本性质,理解和应用比例的基本性质是解答关键。
20.(2分)(2022 裕华区)—个圆柱的体积是36立方米,与它等底等高的圆锥的体积是( )立方米。
A.12 B.24 C.108
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】空间观念.
【答案】A
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【解答】解:3612(立方米)
答:与它等底等高的圆锥的体积是12立方米。
故选:A。
【点评】此题考查了等底等高的圆柱与圆锥的体积的倍数关系的灵活应用。
四.计算题(共5小题,满分25分)
21.(4分)(2021秋 中山市期末)涂色表示下面的分数,并计算。
【考点】分数的加法和减法.
【专题】运算能力.
【答案】;。
【分析】把一个圆平均分成4份,每份是,涂其中2份表示,涂其中1份表示,把它们合起来就是3份,就是。据此解答。
【解答】解:
故答案为:。
【点评】此题考查的目的是理解掌握分数的意义及应用。
22.(6分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
【考点】分数方程求解;解比例.
【专题】简易方程;运算能力.
【答案】x=11,x,x=7。
【分析】(1)根据等式的性质可得x,接下来对方程两边同时除以,求出x的值,即可解答;
(2)根据比例的性质可得(3﹣x)=4x×0.75,接下来根据等式的性质进行求解,即可解答;
(3)根据比例的性质可得6×(x﹣2)=5×(x﹣1),接下来根据等式的性质进行求解,即可解答。
【解答】解:1xx﹣2
x
x=11
4x:(3﹣x):0.75
(3﹣x)=4x×0.75
1x=3x
x=1
1
x
6(x﹣2)=5(x﹣1)
6x﹣12=5x﹣5
6x﹣5x=12﹣5
x=7
【点评】本题是一道关于解方程与解比例的题目,解答本题的关键是掌握等式的性质与比例的性质。
23.(9分)
【考点】分数的四则混合运算.
【专题】运算顺序及法则;运算能力.
【答案】,,。
【分析】本题根据乘法交换律分析填空即可。
【解答】解:
故答案为:,,。
【点评】本题主要考查分数除法的运算法则,除以一个数等于乘这个数的倒数。
24.(3分)一个圆柱的表面积和一个长方形的面积相等,长方形的长等于圆柱的底面周长,已知长方形的面积是138.16cm2,圆柱的底面半径是2cm,圆柱的高是多少?
【考点】圆柱的展开图;圆柱的侧面积和表面积.
【专题】应用题;应用意识.
【答案】9厘米。
【分析】依据圆柱的表面积公式,用圆柱的表面积减去上下底面积,即可求出侧面积;然后用圆柱的侧面积除以底面周长,即可求出圆柱的高。
【解答】解:(138.16﹣3.14×22×2)÷(3.14×2×2)
=113.04÷12.56
=9(厘米)
答:圆柱的高是9厘米。
【点评】本题考查圆柱的表面积,掌握圆柱的表面积公式是解题的关键。
25.(3分)(2023春 唐河县期中)求将下面这个容器倒过来放时,从圆锥的顶点到液面的高是多少厘米?
【考点】圆锥的体积;圆柱的体积.
【专题】应用意识.
【答案】14厘米。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此可以求出圆柱容器中的水倒满圆锥容器需要水的高是(9)厘米,然后用圆锥的高加上圆柱容器剩余水的高即可。
【解答】解:8﹣99
=8﹣3+9
=5+9
=14(厘米)
答:从圆锥的顶点到液面的高是14厘米。
【点评】此题考查的目的是理解掌握等底等高是圆柱与圆锥体积之间的关系及应用。
五.操作题(共1小题,满分5分,每小题5分)
26.(5分)(2023秋 沈丘县期末)下面方格图中小方格的边长是1cm。
(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是 4:1 。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,这个圆的面积是 12.56 平方厘米。
【考点】图形的放大与缩小;比的意义;画圆;圆、圆环的面积.
【专题】几何直观.
【答案】(1)4:1; (2)12.56。
【分析】(1)根据图形放大的方法,将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是长度比的平方比,据此解答即可。
(2)根据圆的画法,在放大的长方形里画一个最大的圆,以长方形的宽为半径,在长方形中画圆,分别用字母O和r标出圆心和半径,再结合圆的面积公式解答即可。
【解答】解:(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);如图:
放大后的长方形面积与原来长方形面积的比是长度比的平方比,所以放大后的长方形面积与原来长方形面积的比是是4:1。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,如图:
3.14×22=12.56(平方厘米)
答:这个圆的面积是12.56平方厘米。
故答案为:4:1;12.56。
【点评】本题考查图形的放大以及圆的画法、圆面积的计算方法等知识,结合题意分析解答即可。
六.解答题(共6小题,满分30分,每小题5分)
27.(5分)铺一间边长6米的正方形客厅,需用288块地砖。用同样的地砖铺边长9米的正方形客厅,需要多少块?(用比例解)
【考点】正、反比例应用题.
【专题】运算能力.
【答案】648块。
【分析】分析题目,根据单位面积需要地砖的块数相同可得288:(6×6)=x:(9×9);接下来根据比例的性质进行求解,即可解答。
【解答】解:设需要x块。
288:(6×6)=x:(9×9)
36x=288×81
x=648
答:需要648块。
【点评】本题是一道关于正比例应用的题目,解答本题的关键是掌握比例的性质。
28.(5分)(2023 吉首市)一个圆锥形沙堆,底面积是56.52m2,高是3m。用这堆沙在10m宽的公路上铺3cm厚的路面,能铺多少米?
【考点】关于圆锥的应用题;长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】188.4米。
【分析】首先根据圆锥的体积底面积×高求出沙堆的体积,然后用沙的体积除以长方体的侧面积=高×宽即可,据此解答。
【解答】解:3厘米=0.03米
56.52×3÷(10×0.03)
=56.52÷0.3
=188.4(米)
答:能铺188.4米。
【点评】此题主要考查圆锥的体积公式、长方体的体积公式在实际生活中的应用,关键是熟记公式。
29.(5分)(2021 姜堰区)张村计划从村里修一条通往进城公路的最短水泥路(如图)。
(1)请你在图中画出这条最短的路线。
(2)量出这条最短的路线的图上距离,并标注在图上。(精确到毫米)
(3)这幅图的比例尺是1:30000,算出这条最短水泥路的实际距离是多少米?
【考点】比例尺应用题;作最短线路图.
【专题】比和比例应用题;应用意识.
【答案】600米。
【分析】(1)根据点到直线的垂直线段最短,即可解答;
(2)量出这条最短的路线的图上距离,并标注在图上;
( 3 )根据实际距离=图上距离÷比例尺,即可解答。
【解答】解:(1)、(2)作图如下:
(3)20600000(毫米)
600000毫米=600米
答:这条最短水泥路的实际距离是600米。
【点评】本题考查的是比例尺应用题,掌握实际距离=图上距离÷比例尺是解答关键。
30.(5分)(2022 息县)一个圆柱体水箱中水高为10厘米,圆柱的底面积为20平方厘米,现将一个石块放进水中(完全淹没),水溢出了30毫升。拿出石块,水面下降了4厘米,石块的体积是 80 立方厘米。
【考点】探索某些实物体积的测量方法.
【专题】立体图形的认识与计算;几何直观.
【答案】80立方厘米。
【分析】石块的体积等于下降的水的体积,用底面积乘下降的厘米数即可。
【解答】解:20×4=80(立方厘米)
答:石块的体积是80立方厘米。
故答案为:80。
【点评】此题主要考查某些实物体积的测量方法。
31.(5分)(2023 万源市)一堆水果,卖掉20%后,又卖掉了120千克,这时卖出的比剩下的多50%,这堆水果原来有多少千克?
【考点】百分数的实际应用.
【专题】分数百分数应用题;应用意识.
【答案】300千克。
【分析】已知卖出两次后,卖出的比剩下的多50%,把卖出两次后剩下的质量看作单位“1”,卖出两次后卖出的就是(1+50%),则这堆水果的总质量就是(1+1+50%),用卖出两次后卖出的占的百分率÷总质量占的百分率×100%,求出卖出两次后卖出的相当于总重量的百分之几;把水果的总质量看作单位“1”,用卖出两次的占总重量的百分率减去第一次卖出的占的百分率,求出第二次卖出的占的百分率;用第二次卖出的质量÷对应的分率,求出这堆水果原来的质量。
【解答】解:(1+50%)÷(1+1+50%)×100%
=150%÷250%×100%
=0.6×100%
=60%
120÷(60%﹣20%)
=120÷40%
=300(千克)
答:这堆水果原来有300千克。
【点评】本题考查百分数的应用。关键是把“卖出两次后卖出的比剩下的多50%”转化为“卖出两次后卖出的占水果总质量的百分之几”。
32.(5分)(2022春 长兴县期中)如图,蜡烛每分钟燃烧的长度一定。(单位:cm)蜡烛最初的长度是多少厘米?
【考点】正、反比例应用题.
【专题】比和比例应用题.
【答案】14.2cm。
【分析】分析可知,蜡烛每分钟燃烧的长度一定,则蜡烛燃烧的长度和燃烧时间成正比例关系;
设蜡烛18分钟燃烧xcm,根据题意可得(18﹣8):(12﹣7)=18:x,至此,再试着进行求解即可。
【解答】解:设蜡烛18分钟燃烧xcm。
(18﹣8):(12﹣7)=18:x
解得x=7.2
7.2+7=14.2(cm)
答:蜡烛未点燃前是14.2cm。
【点评】本题考查的是正比例的应用,关键是确定蜡烛燃烧的长度和燃烧时间成正比例关系。
第1页(共1页)
一.填空题(共10小题,满分20分,每小题2分)
1.(2分)同学们去看电影,小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的 边。
2.(2分)把一根长3米、底面直径是2分米的圆柱形钢材平均截成3个小圆柱,表面积增加了 平方分米。
3.(2分)(2022 永年区)把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是 立方分米。
4.(2分)三个内角的度数比为1:2:3的三角形,它是 三角形。
5.(2分)(2021春 渭滨区期中)一个圆柱和一个圆锥等底等高,它们的体积之和是48dm3,圆柱的体积是 dm3。
6.(2分)阳阳参加诗歌朗诵比赛,七名评委给他的评分分别是9.4分、9.2分、9.9分、9.3分、9.1分、9.7分、9.4分。
(1)这七名评委给阳阳打的平均分是 分。(结果保留两位小数)
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是 分。
7.(2分)(2023春 宜春期中)某校自来水管的内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手走时忘记关闭水龙头,3分钟浪费 升水。
8.(2分)(2022 怀安县)三角形的底一定,面积和高成 比例;三角形的面积一定,底和高成 比例。
9.(2分)(2022春 电白区期中)一个圆柱的底面直径扩大3倍,侧面积也扩大3倍。
10.(2分)(2020秋 兰考县期末)用 个相同的能拼成一个大的正方体。
二.判断题(共5小题,满分10分,每小题2分)
11.(2分)每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。
12.(2分)(2023 邢台模拟)50立方厘米比5平方厘米显然要大得多。
13.(2分)(2024 郾城区)把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是2:3。
14.(2分)(2024 神木市)如果将向东走40m记作+40m,那么向西走20m记作﹣20m。
15.(2分)明辨是非我会断。
(1)一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积不变。
(2)底面积相等的圆柱和圆锥,圆锥的体积一定小于圆柱的体积。
(3)圆柱的底面直径是2cm,高是6.28cm,它的侧面展开后是一个正方形。
(4)如果一个圆柱和一个圆锥的体积相等,那么它们的高的比是3:1。
(5)如果两个圆柱的体积相等,那么它们的侧面积也相等。
(6)圆柱的侧面积等于底面积乘以高。
三.选择题(共5小题,满分10分,每小题2分)
16.(2分)今年春节,某地下午2:00的气温是+4℃;到了晚上9:00,气温是﹣10℃。说明该地( )
A.晚上9:00气温比下午2:00下降了10℃
B.晚上9:00气温是10℃
C.晚上9:00气温比下午2:00的气温高
D.晚上9:00的气温比下午2:00下降了14℃
17.(2分)(2020 红花岗区)一个零件实际长度是3米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )
A.1:20 B.20:1 C.1:50
18.(2分)一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的( )
A.一半 B.2倍 C.4倍 D.8倍
19.(2分)在10、25、40这三个数中添上( )不能组成比例。
A.16 B.100 C. D.8
20.(2分)(2022 裕华区)—个圆柱的体积是36立方米,与它等底等高的圆锥的体积是( )立方米。
A.12 B.24 C.108
四.计算题(共5小题,满分25分)
21.(4分)(2021秋 中山市期末)涂色表示下面的分数,并计算。
22.(6分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
23.(9分)
24.(3分)一个圆柱的表面积和一个长方形的面积相等,长方形的长等于圆柱的底面周长,已知长方形的面积是138.16cm2,圆柱的底面半径是2cm,圆柱的高是多少?
25.(3分)(2023春 唐河县期中)求将下面这个容器倒过来放时,从圆锥的顶点到液面的高是多少厘米?
五.操作题(共1小题,满分5分,每小题5分)
26.(5分)(2023秋 沈丘县期末)下面方格图中小方格的边长是1cm。
(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是 。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,这个圆的面积是 平方厘米。
六.解答题(共6小题,满分30分,每小题5分)
27.(5分)铺一间边长6米的正方形客厅,需用288块地砖。用同样的地砖铺边长9米的正方形客厅,需要多少块?(用比例解)
28.(5分)(2023 吉首市)一个圆锥形沙堆,底面积是56.52m2,高是3m。用这堆沙在10m宽的公路上铺3cm厚的路面,能铺多少米?
29.(5分)(2021 姜堰区)张村计划从村里修一条通往进城公路的最短水泥路(如图)。
(1)请你在图中画出这条最短的路线。
(2)量出这条最短的路线的图上距离,并标注在图上。(精确到毫米)
(3)这幅图的比例尺是1:30000,算出这条最短水泥路的实际距离是多少米?
30.(5分)(2022 息县)一个圆柱体水箱中水高为10厘米,圆柱的底面积为20平方厘米,现将一个石块放进水中(完全淹没),水溢出了30毫升。拿出石块,水面下降了4厘米,石块的体积是 立方厘米。
31.(5分)(2023 万源市)一堆水果,卖掉20%后,又卖掉了120千克,这时卖出的比剩下的多50%,这堆水果原来有多少千克?
32.(5分)(2022春 长兴县期中)如图,蜡烛每分钟燃烧的长度一定。(单位:cm)蜡烛最初的长度是多少厘米?
上海市2024-2025学年六年级下学期期中模拟预测数学试卷
参考答案与试题解析
一.填空题(共10小题,满分20分,每小题2分)
1.(2分)同学们去看电影,小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的 右 边。
【考点】位置.
【专题】应用意识.
【答案】右。
【分析】座位的顺序从左向右的顺序是:小丁丁、小巧、小亚,所以小亚在小丁丁的右边。
【解答】解:小丁丁坐在小巧的左边,小亚坐在小巧的右边,那么小亚坐在小丁丁的右边。
故答案为:右。
【点评】本题考查位置,解决本题的关键是明确座位的顺序。
2.(2分)把一根长3米、底面直径是2分米的圆柱形钢材平均截成3个小圆柱,表面积增加了 12.56 平方分米。
【考点】圆柱的侧面积、表面积和体积.
【专题】运算能力.
【答案】12.56。
【分析】表面积增加部分就是指截取后增加的底面的面积;根据圆柱的截取方法可知,截成3个小圆柱,需要截取2次,那么增加了4个底面直径为2分米的圆柱的底面积,由此利用圆柱的底面积公式代入数据即可解决问题。
【解答】解:3.14×(2÷2)2×4
=3.14×1×4
=12.56(平方分米)
答:表面积增加了12.56平方分米。
故答案为:12.56。
【点评】正确找出增加的面是解决本题的关键。
3.(2分)(2022 永年区)把一个棱长为6分米的正方体木块削成一个最大的圆锥,这个圆锥的体积是 56.52 立方分米。
【考点】圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】56.52。
【分析】这个圆锥的底面直径是6分米,高是6分米,再根据圆锥的体积=底面积×高÷3,解答即可。
【解答】解:3.14×(6÷2)2×6
3.14×9×6
=3.14×18
=56.52(立方分米)
答:这个圆锥的体积是56.52立方分米。
【点评】熟练掌握圆锥的体积公式,是解答此题的关键。
4.(2分)三个内角的度数比为1:2:3的三角形,它是 直角 三角形。
【考点】按比例分配应用题.
【专题】比和比例应用题;应用意识.
【答案】直角。
【分析】根据三角形的内角和是180°,把180°按1:2:3进行分配,求出最大角的度数,即可解答。
【解答】解:180°
=180°
=90°
答:它是直角三角形。
故答案为:直角。
【点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
5.(2分)(2021春 渭滨区期中)一个圆柱和一个圆锥等底等高,它们的体积之和是48dm3,圆柱的体积是 36 dm3。
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】36。
【分析】等底等高的圆柱的体积是圆锥的体积的3倍,把圆锥体积看作单位“1”,那么等底等高的圆柱和圆锥的体积之和是(1+3)倍,已知一个数的几倍是多少求这个数,用除法计算,由此即可解答。
【解答】解:48÷(1+3)
=48÷4
=12(dm3)
12×3=36(dm3)
答:圆柱的体积是36dm3。
故答案为:36。
【点评】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
6.(2分)阳阳参加诗歌朗诵比赛,七名评委给他的评分分别是9.4分、9.2分、9.9分、9.3分、9.1分、9.7分、9.4分。
(1)这七名评委给阳阳打的平均分是 9.43 分。(结果保留两位小数)
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是 9.4 分。
【考点】平均数的含义及求平均数的方法.
【专题】平均数问题.
【答案】(1)9.43;(2)9.4。
【分析】对于(1),利用加法求出七位评委的总分,然后除以人数即可求出答案;
对于(2),去掉一个最高分、去掉一个最低分,用与(1)相同的方法解答。
【解答】解:(1)这七名评委给阳阳打的平均分是:
(9.4+9.2+9.9+9.3+9.1+9.7+9.4)÷7
=66÷7
≈9.43(分)
答:这七名评委给阳阳打的平均分是9.43分。
(2)按照去掉一个最高分、一个最低分的规则进行计算,阳阳的平均分是:
(9.4+9.2+9.3+9.7+9.4)÷5
=47÷5
=9.4(分)
答:阳阳的平均分是9.4分。
故答案为:9.43,9.4。
【点评】这是一道关于求平均数的题目,关键是掌握平均数的求法。
7.(2分)(2023春 宜春期中)某校自来水管的内直径是2cm,水管内水流速度是每秒10cm。一个同学洗手走时忘记关闭水龙头,3分钟浪费 5.652 升水。
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】5.652。
【分析】分析题意,先求每秒流出的水的体积,即求直径是2cm,高是10cm的圆柱体积,用直径除以2,求出半径,将相关数据代入圆柱的体积公式即可求解;然后用每秒流出的水的体积乘以时间(注意单位的换算),即可求出3分钟流出的水的体积。
【解答】解:3分=180秒
3.14×(2÷2)2×10×180
=3.14×1800
=5652(立方厘米)
5652立方厘米=5.652升
答:3分钟浪费5.652升水。
故答案为:5.652。
【点评】本题主要考查圆柱体积的实际运用,关键是熟练掌握圆柱的体积公式。
8.(2分)(2022 怀安县)三角形的底一定,面积和高成 正 比例;三角形的面积一定,底和高成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:(1)因为三角形的面积=底×高÷2,
所以三角形的面积×2÷高=底(一定),
符合正比例的意义,
所以三角形的底一定,面积和高成正比例;
(2)因为三角形的面积=底×高÷2,
即底×高=长方形的面积×2(一定),
符合反比例的意义,
所以三角形形的面积一定,底和高成反比例。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
9.(2分)(2022春 电白区期中)一个圆柱的底面直径扩大3倍,侧面积也扩大3倍。 ×
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】因为圆柱的侧面积公式S=πdh可得,若高不变时,圆柱体的底面直径扩大3倍,它的侧面积就扩大3倍,据此解答。
【解答】解:圆柱的高不变,圆柱体的底面直径扩大3倍,它的侧面积就扩大3倍;但是本题没有说明高不变这个条件;
故答案为:×。
【点评】本题主要是利用圆柱的侧面积公式与积的变化规律解决问题。
10.(2分)(2020秋 兰考县期末)用 8 个相同的能拼成一个大的正方体。
【考点】简单的立方体切拼问题.
【专题】空间观念.
【答案】8。
【分析】用小正方体拼组大正方体时,每个棱长上至少需要2个小正方体,由此即可解答。
【解答】解:用小正方体拼组大正方体时,每个棱长上至少需要2个小正方体,
所以拼成一个大正方体至少需要小正方体:2×2×2=8(个)
答:用8个相同的能拼成一个大的正方体。
故答案为:8。
【点评】抓住小正方体拼组大正方体的方法,是解决此类问题的关键。
二.判断题(共5小题,满分10分,每小题2分)
11.(2分)每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;推理能力.
【答案】√
【分析】判断两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。据此进行判断即可。
【解答】解:因为订餐的总钱数÷订餐的份数=每份快餐的单价(一定),因此每份快餐的单价一定,订快餐的份数和所用的总钱数成正比例。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(2分)(2023 邢台模拟)50立方厘米比5平方厘米显然要大得多。 ×
【考点】体积、容积及其单位.
【专题】综合判断题;应用意识.
【答案】×
【分析】立方厘米表示体积单位,平方厘米表示面积单位,无法比较。
【解答】解:立方厘米表示体积单位,平方厘米表示面积单位,无法比较。
50立方厘米比5平方厘米显然要大得多的说法错误。
故答案为:×。
【点评】本题考查的主要内容是体积单位的认识问题。
13.(2分)(2024 郾城区)把一个圆柱削成一个最大的圆锥,削去部分与圆柱体积的比是2:3。 √
【考点】圆锥的体积;圆柱的体积.
【专题】综合判断题;立体图形的认识与计算.
【答案】√
【分析】圆柱的体积是和它等底等高的圆锥体积的三倍,把圆柱削成最大的圆锥,则圆锥与圆柱等底等高,削去了两个圆锥的体积;也就是削去部分的体积是圆锥体积的2倍;据此判断。
【解答】解:圆柱体削成一个最大的圆锥体,
则:V圆柱=3V圆锥
(V圆柱﹣V圆锥):V圆柱
V圆柱:V圆柱
=2:3
答:削去部分的体积与圆柱的体积的比是2:3。
故题干的说法是正确。
故答案为:√。
【点评】此题考查等底等高的圆柱和圆锥体积间的关系。
14.(2分)(2024 神木市)如果将向东走40m记作+40m,那么向西走20m记作﹣20m。 √
【考点】负数的意义及其应用.
【专题】整数的认识;数感.
【答案】√
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,由此直接得出结论即可。
【解答】解:如果向东走600m记作+600m,那么向西走20m记作﹣20m,所以本题说法正确。
故答案为:√。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
15.(2分)明辨是非我会断。
(1)一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积不变。 ×
(2)底面积相等的圆柱和圆锥,圆锥的体积一定小于圆柱的体积。 ×
(3)圆柱的底面直径是2cm,高是6.28cm,它的侧面展开后是一个正方形。 √
(4)如果一个圆柱和一个圆锥的体积相等,那么它们的高的比是3:1。 ×
(5)如果两个圆柱的体积相等,那么它们的侧面积也相等。 ×
(6)圆柱的侧面积等于底面积乘以高。 ×
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】×,×,√,×,×,×
【分析】圆柱的体积=圆柱的底面积×高,圆柱的体积由圆柱的底面积和高两个因素共同决定的。
圆柱的侧面展开图是一个长方形,长是圆柱的底面周长,宽是圆柱的高。
若圆柱的底面周长=圆柱的高,则它的展开图是正方形。
【解答】解:1.一个圆柱的高扩大到原来的2倍,底面半径缩小到原来的,体积变为原来的,故原题说法错误;
2.底面积相等的圆柱和圆锥,没有给出高,无法判断圆锥的体积与圆柱的体积的大小,故原题说法错误;
3.圆柱的底面直径是2cm,则底面周长是3.14×2=6.28cm,高是6.28cm,它的侧面展开后是一个正方形,故原题说法正确;
4.如果一个圆柱和一个圆锥的体积相等,它们的高的比无法确定,故原题说法错误;
5.如果两个圆柱的体积相等,则底面积与高的乘积相等,侧面积的大小无法判断,故原题说法错误;
6.圆柱的侧面积等于底面周长乘以高,故原题说法错误。
故答案为:1.×;2.×;3. ;4.×;5.×;6.×。
【点评】本题是一道有关圆锥的体积、圆柱的体积的题目,解决本题的关键是利用公式计算即可。
三.选择题(共5小题,满分10分,每小题2分)
16.(2分)今年春节,某地下午2:00的气温是+4℃;到了晚上9:00,气温是﹣10℃。说明该地( )
A.晚上9:00气温比下午2:00下降了10℃
B.晚上9:00气温是10℃
C.晚上9:00气温比下午2:00的气温高
D.晚上9:00的气温比下午2:00下降了14℃
【考点】正、负数的运算.
【专题】数的运算.
【答案】D
【分析】用下午2:00的气温减去晚上9:00的气温即可。
【解答】解:4﹣(﹣10)
=4+10
=14(℃)
答:晚上9:00的气温比下午2:00下降了14℃。
故选:D。
【点评】根据正负数的运算方法,解答此题即可。
17.(2分)(2020 红花岗区)一个零件实际长度是3米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )
A.1:20 B.20:1 C.1:50
【考点】比例尺.
【专题】比和比例;应用意识.
【答案】C
【分析】根据比例尺=图上距离:实际距离,代入数值计算即可。
【解答】解:6厘米:3米
=6:300
=1:50
答:这张图纸的比例尺是1:50。
故选:C。
【点评】此题主要考查比例尺、图上距离、实际距离三者的关系式:比例尺=图上距离:实际距离。
18.(2分)一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的( )
A.一半 B.2倍 C.4倍 D.8倍
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】B
【分析】长方体的体积与正方体的体积都等于底面积乘高,当长方体与正方体的体积相等时,它们的底面积与高的乘积相等;再根据长方体的高是正方体的高的一半,即可得出长方体底面积与正方体底面积的关系。
【解答】解:由分析可得:一个长方体和一个正方体的体积相等,且长方体的高是正方体的高的一半,长方体的底面积是正方体底面积的2倍。
故选:B。
【点评】本题是一道关于长方体和正方体体积的题目,掌握体积计算公式是解题的关键。
19.(2分)在10、25、40这三个数中添上( )不能组成比例。
A.16 B.100 C. D.8
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】D
【分析】根据比例的基本性质内项之积等于外项之积,即可判断。
【解答】解:A.10×40=400
25×16=400
能组成比例。
B.25×40=1000
10×100=1000
能组成比例。
C.40250
10×25=250
能组成比例。
D.10×25=250
40×8=320
不能组成比例。
故选:D。
【点评】本题考查的是比例的基本性质,理解和应用比例的基本性质是解答关键。
20.(2分)(2022 裕华区)—个圆柱的体积是36立方米,与它等底等高的圆锥的体积是( )立方米。
A.12 B.24 C.108
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【专题】空间观念.
【答案】A
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【解答】解:3612(立方米)
答:与它等底等高的圆锥的体积是12立方米。
故选:A。
【点评】此题考查了等底等高的圆柱与圆锥的体积的倍数关系的灵活应用。
四.计算题(共5小题,满分25分)
21.(4分)(2021秋 中山市期末)涂色表示下面的分数,并计算。
【考点】分数的加法和减法.
【专题】运算能力.
【答案】;。
【分析】把一个圆平均分成4份,每份是,涂其中2份表示,涂其中1份表示,把它们合起来就是3份,就是。据此解答。
【解答】解:
故答案为:。
【点评】此题考查的目的是理解掌握分数的意义及应用。
22.(6分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
【考点】分数方程求解;解比例.
【专题】简易方程;运算能力.
【答案】x=11,x,x=7。
【分析】(1)根据等式的性质可得x,接下来对方程两边同时除以,求出x的值,即可解答;
(2)根据比例的性质可得(3﹣x)=4x×0.75,接下来根据等式的性质进行求解,即可解答;
(3)根据比例的性质可得6×(x﹣2)=5×(x﹣1),接下来根据等式的性质进行求解,即可解答。
【解答】解:1xx﹣2
x
x=11
4x:(3﹣x):0.75
(3﹣x)=4x×0.75
1x=3x
x=1
1
x
6(x﹣2)=5(x﹣1)
6x﹣12=5x﹣5
6x﹣5x=12﹣5
x=7
【点评】本题是一道关于解方程与解比例的题目,解答本题的关键是掌握等式的性质与比例的性质。
23.(9分)
【考点】分数的四则混合运算.
【专题】运算顺序及法则;运算能力.
【答案】,,。
【分析】本题根据乘法交换律分析填空即可。
【解答】解:
故答案为:,,。
【点评】本题主要考查分数除法的运算法则,除以一个数等于乘这个数的倒数。
24.(3分)一个圆柱的表面积和一个长方形的面积相等,长方形的长等于圆柱的底面周长,已知长方形的面积是138.16cm2,圆柱的底面半径是2cm,圆柱的高是多少?
【考点】圆柱的展开图;圆柱的侧面积和表面积.
【专题】应用题;应用意识.
【答案】9厘米。
【分析】依据圆柱的表面积公式,用圆柱的表面积减去上下底面积,即可求出侧面积;然后用圆柱的侧面积除以底面周长,即可求出圆柱的高。
【解答】解:(138.16﹣3.14×22×2)÷(3.14×2×2)
=113.04÷12.56
=9(厘米)
答:圆柱的高是9厘米。
【点评】本题考查圆柱的表面积,掌握圆柱的表面积公式是解题的关键。
25.(3分)(2023春 唐河县期中)求将下面这个容器倒过来放时,从圆锥的顶点到液面的高是多少厘米?
【考点】圆锥的体积;圆柱的体积.
【专题】应用意识.
【答案】14厘米。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆柱的高是圆锥高的,据此可以求出圆柱容器中的水倒满圆锥容器需要水的高是(9)厘米,然后用圆锥的高加上圆柱容器剩余水的高即可。
【解答】解:8﹣99
=8﹣3+9
=5+9
=14(厘米)
答:从圆锥的顶点到液面的高是14厘米。
【点评】此题考查的目的是理解掌握等底等高是圆柱与圆锥体积之间的关系及应用。
五.操作题(共1小题,满分5分,每小题5分)
26.(5分)(2023秋 沈丘县期末)下面方格图中小方格的边长是1cm。
(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是 4:1 。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,这个圆的面积是 12.56 平方厘米。
【考点】图形的放大与缩小;比的意义;画圆;圆、圆环的面积.
【专题】几何直观.
【答案】(1)4:1; (2)12.56。
【分析】(1)根据图形放大的方法,将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);放大后的长方形面积与原来长方形面积的比是长度比的平方比,据此解答即可。
(2)根据圆的画法,在放大的长方形里画一个最大的圆,以长方形的宽为半径,在长方形中画圆,分别用字母O和r标出圆心和半径,再结合圆的面积公式解答即可。
【解答】解:(1)将长方形ABCD各边放大到原来的2倍,画出放大后的图形,并使点A的对应点的位置在(10,5);如图:
放大后的长方形面积与原来长方形面积的比是长度比的平方比,所以放大后的长方形面积与原来长方形面积的比是是4:1。
(2)在放大的长方形里画一个最大的圆,分别用字母O和r标出圆心和半径,如图:
3.14×22=12.56(平方厘米)
答:这个圆的面积是12.56平方厘米。
故答案为:4:1;12.56。
【点评】本题考查图形的放大以及圆的画法、圆面积的计算方法等知识,结合题意分析解答即可。
六.解答题(共6小题,满分30分,每小题5分)
27.(5分)铺一间边长6米的正方形客厅,需用288块地砖。用同样的地砖铺边长9米的正方形客厅,需要多少块?(用比例解)
【考点】正、反比例应用题.
【专题】运算能力.
【答案】648块。
【分析】分析题目,根据单位面积需要地砖的块数相同可得288:(6×6)=x:(9×9);接下来根据比例的性质进行求解,即可解答。
【解答】解:设需要x块。
288:(6×6)=x:(9×9)
36x=288×81
x=648
答:需要648块。
【点评】本题是一道关于正比例应用的题目,解答本题的关键是掌握比例的性质。
28.(5分)(2023 吉首市)一个圆锥形沙堆,底面积是56.52m2,高是3m。用这堆沙在10m宽的公路上铺3cm厚的路面,能铺多少米?
【考点】关于圆锥的应用题;长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】188.4米。
【分析】首先根据圆锥的体积底面积×高求出沙堆的体积,然后用沙的体积除以长方体的侧面积=高×宽即可,据此解答。
【解答】解:3厘米=0.03米
56.52×3÷(10×0.03)
=56.52÷0.3
=188.4(米)
答:能铺188.4米。
【点评】此题主要考查圆锥的体积公式、长方体的体积公式在实际生活中的应用,关键是熟记公式。
29.(5分)(2021 姜堰区)张村计划从村里修一条通往进城公路的最短水泥路(如图)。
(1)请你在图中画出这条最短的路线。
(2)量出这条最短的路线的图上距离,并标注在图上。(精确到毫米)
(3)这幅图的比例尺是1:30000,算出这条最短水泥路的实际距离是多少米?
【考点】比例尺应用题;作最短线路图.
【专题】比和比例应用题;应用意识.
【答案】600米。
【分析】(1)根据点到直线的垂直线段最短,即可解答;
(2)量出这条最短的路线的图上距离,并标注在图上;
( 3 )根据实际距离=图上距离÷比例尺,即可解答。
【解答】解:(1)、(2)作图如下:
(3)20600000(毫米)
600000毫米=600米
答:这条最短水泥路的实际距离是600米。
【点评】本题考查的是比例尺应用题,掌握实际距离=图上距离÷比例尺是解答关键。
30.(5分)(2022 息县)一个圆柱体水箱中水高为10厘米,圆柱的底面积为20平方厘米,现将一个石块放进水中(完全淹没),水溢出了30毫升。拿出石块,水面下降了4厘米,石块的体积是 80 立方厘米。
【考点】探索某些实物体积的测量方法.
【专题】立体图形的认识与计算;几何直观.
【答案】80立方厘米。
【分析】石块的体积等于下降的水的体积,用底面积乘下降的厘米数即可。
【解答】解:20×4=80(立方厘米)
答:石块的体积是80立方厘米。
故答案为:80。
【点评】此题主要考查某些实物体积的测量方法。
31.(5分)(2023 万源市)一堆水果,卖掉20%后,又卖掉了120千克,这时卖出的比剩下的多50%,这堆水果原来有多少千克?
【考点】百分数的实际应用.
【专题】分数百分数应用题;应用意识.
【答案】300千克。
【分析】已知卖出两次后,卖出的比剩下的多50%,把卖出两次后剩下的质量看作单位“1”,卖出两次后卖出的就是(1+50%),则这堆水果的总质量就是(1+1+50%),用卖出两次后卖出的占的百分率÷总质量占的百分率×100%,求出卖出两次后卖出的相当于总重量的百分之几;把水果的总质量看作单位“1”,用卖出两次的占总重量的百分率减去第一次卖出的占的百分率,求出第二次卖出的占的百分率;用第二次卖出的质量÷对应的分率,求出这堆水果原来的质量。
【解答】解:(1+50%)÷(1+1+50%)×100%
=150%÷250%×100%
=0.6×100%
=60%
120÷(60%﹣20%)
=120÷40%
=300(千克)
答:这堆水果原来有300千克。
【点评】本题考查百分数的应用。关键是把“卖出两次后卖出的比剩下的多50%”转化为“卖出两次后卖出的占水果总质量的百分之几”。
32.(5分)(2022春 长兴县期中)如图,蜡烛每分钟燃烧的长度一定。(单位:cm)蜡烛最初的长度是多少厘米?
【考点】正、反比例应用题.
【专题】比和比例应用题.
【答案】14.2cm。
【分析】分析可知,蜡烛每分钟燃烧的长度一定,则蜡烛燃烧的长度和燃烧时间成正比例关系;
设蜡烛18分钟燃烧xcm,根据题意可得(18﹣8):(12﹣7)=18:x,至此,再试着进行求解即可。
【解答】解:设蜡烛18分钟燃烧xcm。
(18﹣8):(12﹣7)=18:x
解得x=7.2
7.2+7=14.2(cm)
答:蜡烛未点燃前是14.2cm。
【点评】本题考查的是正比例的应用,关键是确定蜡烛燃烧的长度和燃烧时间成正比例关系。
第1页(共1页)
同课章节目录
