初中数学苏科版八年级下册 《第9章中心对称图形--平行四边形》单元测试卷(含解析)
文档属性
| 名称 | 初中数学苏科版八年级下册 《第9章中心对称图形--平行四边形》单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 09:48:25 | ||
图片预览


文档简介
《第9章中心对称图形--平行四边形》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.为培养学生利用现代信息技术解决数学问题的能力,十堰经开区数学教研室在本学期组织辖区内初中生开展了“运用几何画板,探寻美丽的数学世界”比赛活动.下列图形是部分参赛作品,是中心对称图形的是( )
A. B.
C. D.
2.如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
3.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
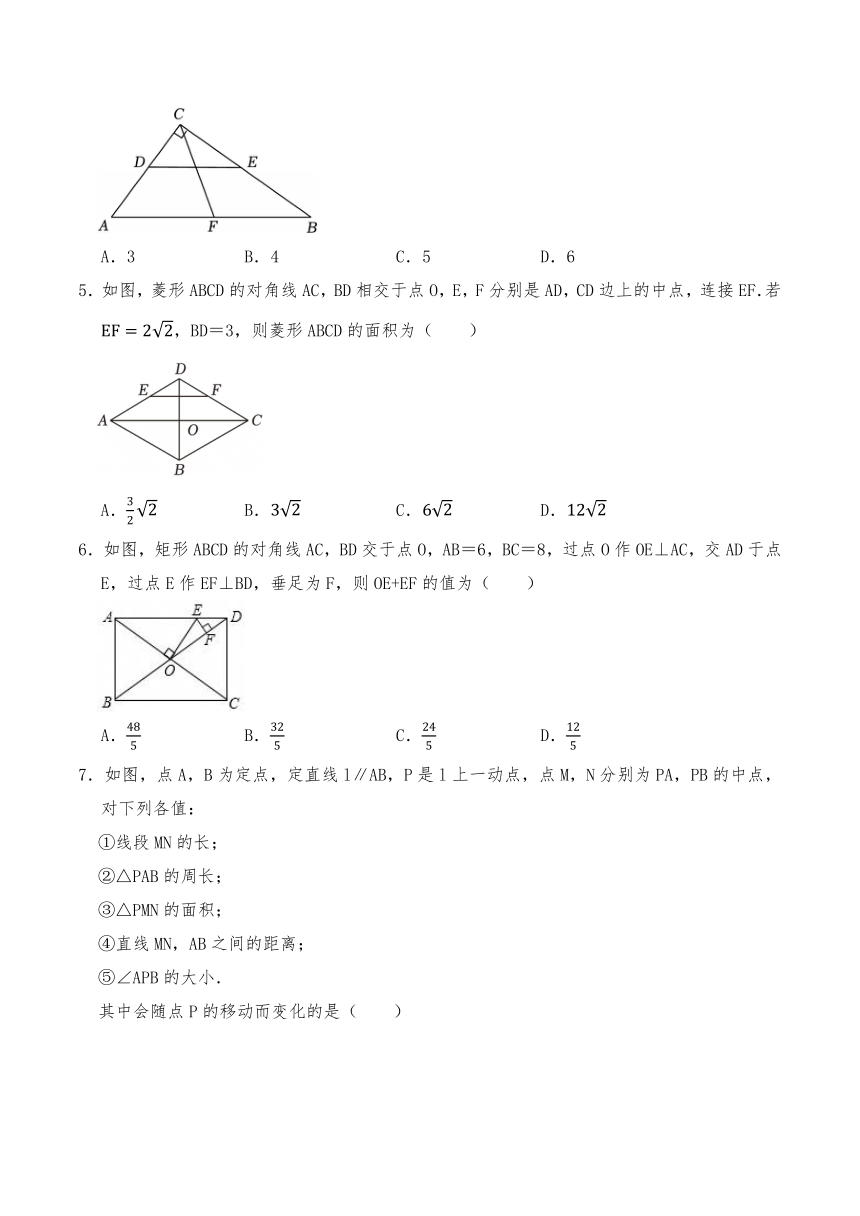
4.如图,在Rt△ABC中,∠ACB=90°,CF是AB边上的中线,DE是△ABC的中位线,若CF=6,则DE的长( )
A.3 B.4 C.5 D.6
5.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若,BD=3,则菱形ABCD的面积为( )
A. B. C. D.
6.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
A. B. C. D.
7.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
8.如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=θ1,∠PBA=θ2,∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°,则( )
A.(θ1+θ4)﹣(θ2+θ3)=30°
B.(θ2+θ4)﹣(θ1+θ3)=40°
C.(θ1+θ2)﹣(θ3+θ4)=70°
D.(θ1+θ2)+(θ3+θ4)=180°
9.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B.2 C.2 D.4
10.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共8小题,满分24分,每小题3分)
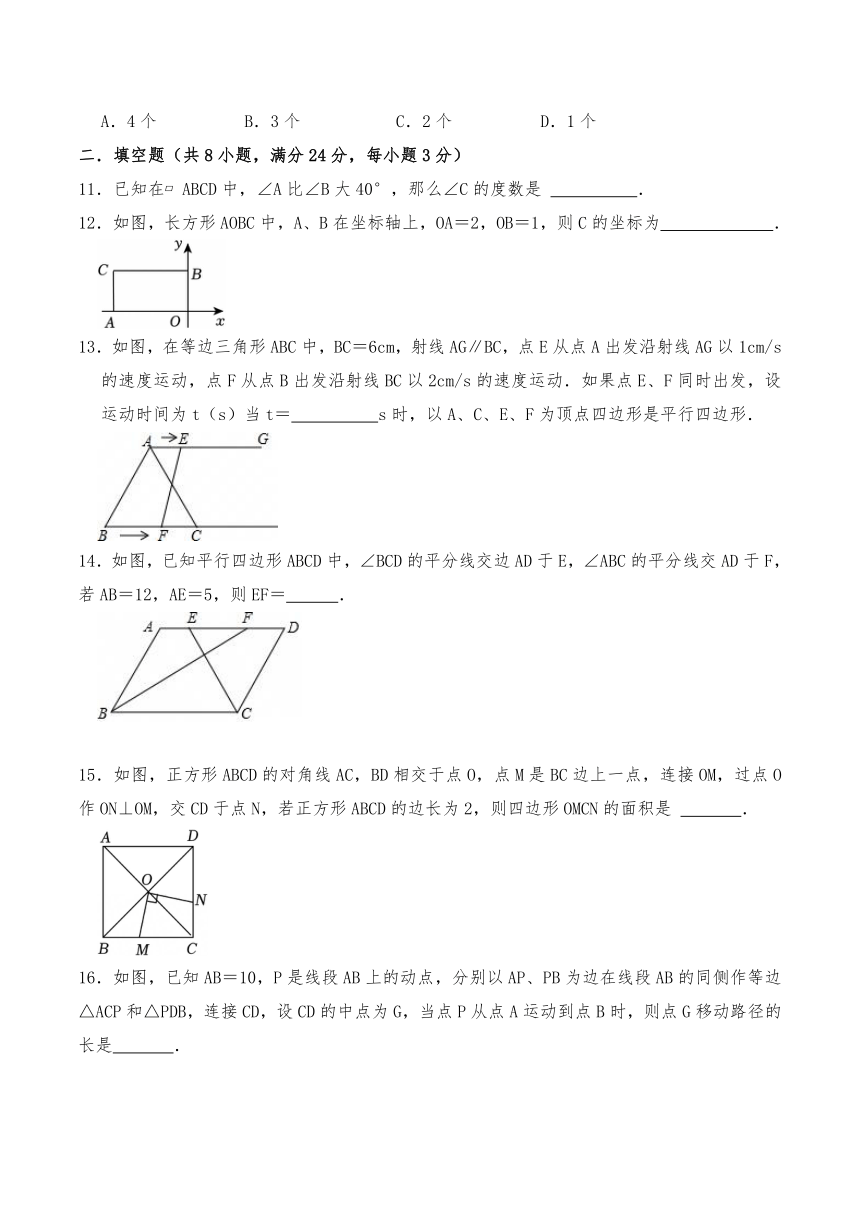
11.已知在 ABCD中,∠A比∠B大40°,那么∠C的度数是 .
12.如图,长方形AOBC中,A、B在坐标轴上,OA=2,OB=1,则C的坐标为 .
13.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t= s时,以A、C、E、F为顶点四边形是平行四边形.
14.如图,已知平行四边形ABCD中,∠BCD的平分线交边AD于E,∠ABC的平分线交AD于F,若AB=12,AE=5,则EF= .
15.如图,正方形ABCD的对角线AC,BD相交于点O,点M是BC边上一点,连接OM,过点O作ON⊥OM,交CD于点N,若正方形ABCD的边长为2,则四边形OMCN的面积是 .
16.如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是 .
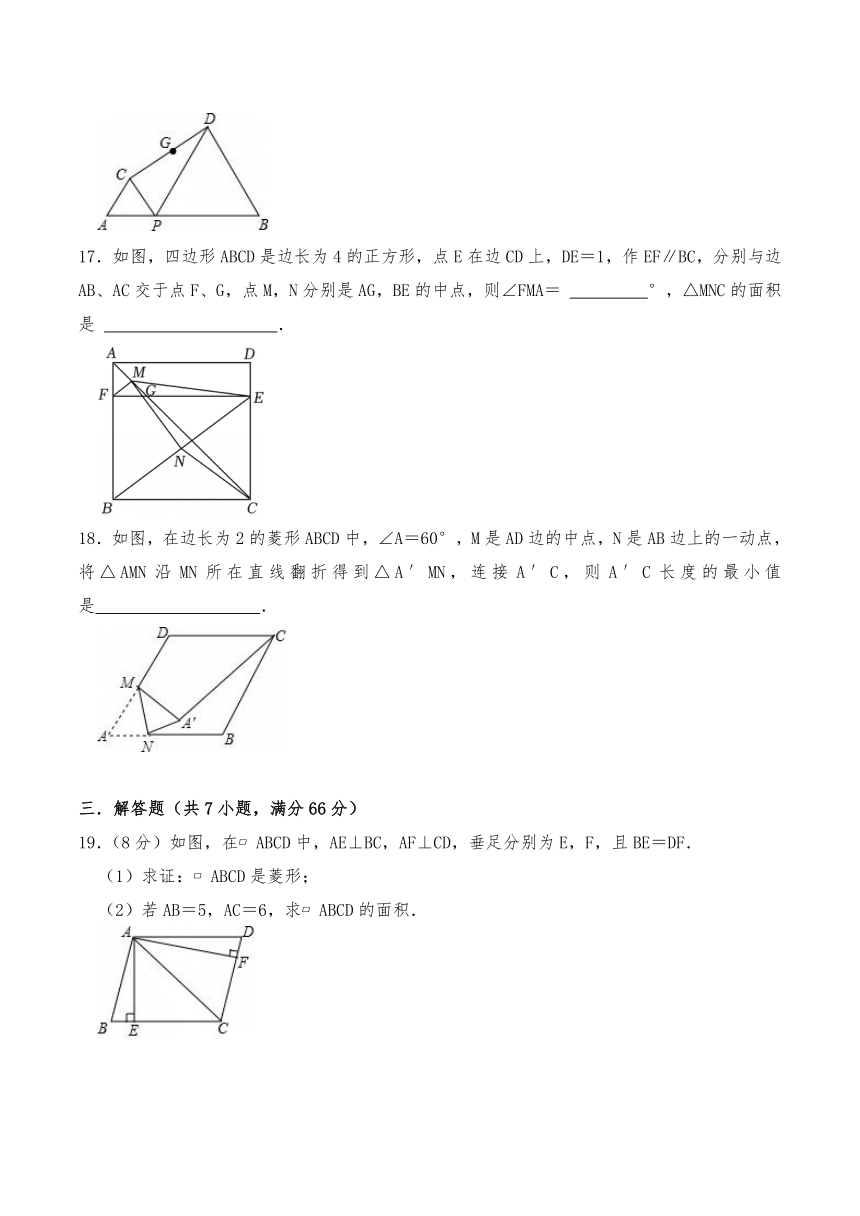
17.如图,四边形ABCD是边长为4的正方形,点E在边CD上,DE=1,作EF∥BC,分别与边AB、AC交于点F、G,点M,N分别是AG,BE的中点,则∠FMA= °,△MNC的面积是 .
18.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
三.解答题(共7小题,满分66分)
19.(8分)如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
20.(6分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)作出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)若将△ABC绕点P旋转得到△A2B2C2,则点P的坐标为 .
A.(0,1)
B.(1,2)
C.(1,1)
D.(1,0)
21.(8分)如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
22.(8分)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
23.(12分)【模型呈现】在正方形学习过程中,我们发现下面的结论:如图1,正方形ABCD中,点P为线段BC上一个动点,若线段MN垂直AP于点E,交线段AB于点M,交线段CD于点N,则AP=MN.
(1)如图②,将边长为40的正方形ABCD折叠,使得点B落在CD上的点E处.若折痕FG=41,则CE= .
【继续探索】
(2)如图③,正方形ABCD中,点P为线段BC上一动点,若MN垂直平分线段AP,分别交AB,AP,BD,
DC于点M,E,F,N.求证:EF=ME+FN.
(3)如图④,在正方形ABCD中,E、F分别为AD,BC上的点,作DM⊥EF于M,在MF上截取MN=DM,
连接BN,G为BN中点,连接CG,CM.请依题意补全图形,若CG=2,则CM= .
24.(12分)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(6,8),点D为对角线OB的中点.点P是OC边上一动点,直线PD交AB边于点E.
(1)求证:四边形OPBE为平行四边形;
(2)若△ODP的面积与四边形OAED的面积之比为1:3,求点P的坐标;
(3)设点Q是x轴上方平面内的一点,以点O、D、P、Q为顶点的四边形是菱形,直接写出点Q的坐标.
25.(12分)平面直角坐标系不仅可以研究函数,还可以研究并解决很多图形以及图形变换问题.
(1)如图①,在菱形OABC中,若点A(3,4),则点B坐标为 ;
(2)如图②,线段AB、CD关于点P对称,若点A(3,3)、B(5,1)、D(﹣3,﹣1),则点C的坐标为 ;
(3)如图③,在直角坐标系中,点A、B的坐标分别为(﹣1,2)、(﹣5,1),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标为 ;
(4)如图④,已知正方形ABCD的边长为5,E、F分别是边CD、AD上的点,BE、CF交于点P,CE=DF=2,写出求AP长的解题思路.
参考答案
一.选择题
1.
【分析】把一个图形绕某一点旋转180°后,能够与原图形重合,那么这个图形就叫做中心对称图形,据此分析判断即可.
【解答】解:中心对称图形的概念逐项分析判断如下:
A、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
B、绕某一点旋转180°后,能够与原图形重合,是中心对称图形,故符合题意;
C、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
D、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
故选:B.
2.
【分析】直接根据旋转的性质逐一判断即可.
【解答】解:∵△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,
∴∠DBE=∠ABC=45°,∠ABD=∠CBE=60°,
故选项B、C、D正确,
由已知条件无法得出∠BED=30°,
故选项A错误,
故选:A.
3.
【分析】由菱形的判定与性质即可得出A、B、D正确,C不正确.
【解答】解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.∵菱形的对角线互相垂直且平分,
∴选项C不正确;
D.菱形的邻边相等;正确;
故选:C.
4.
【分析】根据直角三角形斜边上的直线的性质得出AB的长,再根据三角形中位线定理得出结果.
【解答】解:在Rt△ABC中,∠ACB=90°,CF是AB边上的中线,
∴AB=2CF=12,
∵DE是△ABC的中位线,
∴DE6,
故选:D.
5.
【分析】首先根据三角形中位线定理得到,再计算菱形的面积即可.
【解答】解:∵E,F分别是AD,CD边上的中点,,
∴,
∵四边形ABCD是菱形,
∴菱形ABCD的面积,
故选:C.
6.
【分析】依据矩形的性质即可得到△AOD的面积为12,再根据S△AOD=S△AOE+S△DOE,即可得到OE+EF的值.
【解答】解:∵AB=6,BC=8,
∴矩形ABCD的面积为48,AC10,
∴AO=DOAC=5,
∵对角线AC,BD交于点O,
∴△AOD的面积为12,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,即12AO×EODO×EF,
∴125×EO5×EF,
∴5(EO+EF)=24,
∴EO+EF,
故选:C.
7.
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得MNAB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
【解答】解:∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MNAB,
即线段MN的长度不变,故①错误;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②正确;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③错误;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小点P的移动而变化,故⑤正确.
综上所述,会随点P的移动而变化的是②⑤.
故选:B.
8.
【分析】依据矩形的性质以及三角形内角和定理,可得θ2﹣θ1=10°,θ4﹣θ3=40°,两式相减即可得到(θ1+θ4)﹣(θ2+θ3)=30°.
【解答】解:∵矩形ABCD,
∴∠BAD=∠BCD=90°,
∴∠BAP=90°﹣θ1,∠DCP=90°﹣θ3,
∴△ABP中,90°﹣θ1+θ2+80°=180°,即θ2﹣θ1=10°,①
△DCP中,90°﹣θ3+θ4+50°=180°,即θ4﹣θ3=40°,②
由②﹣①,可得(θ4﹣θ3)﹣(θ2﹣θ1)=30°,
即(θ1+θ4)﹣(θ2+θ3)=30°,
故选:A.
9.
【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.
【解答】解:如图,连接AE,
∵四边形DEFG是正方形,
∴∠EDG=90°,EF=DE=DG,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴d1+d2+d3=EF+CF+AE,
∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,
连接AC,
∴d1+d2+d3最小值为AC,
在Rt△ABC中,ACAB=2,
∴d1+d2+d3最小=AC=2,
故选:C.
10.
【分析】①利用线段垂直平分线的性质的逆定理可得结论;
②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;
③可证明∠CDE=∠DFE;
④可通过面积转化进行解答.
【解答】解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠CBF=30°,∠BEO=60°,
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∴S△AOE:S△BCM=2S△CMF:S△BCM,
∵∠FCO=30°,
∴FM,BMCM,
∴,
∴S△AOE:S△BCM=2:3,
故④正确;
所以其中正确结论的个数为3个;
故选:B.
二.填空题
11.
【分析】根据平行四边形的对角相等,邻角之和为180°,即可求出该平行四边形各个内角的度数.
【解答】解:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠A+∠B=180°,
又∵∠A﹣∠B=40°,
∴∠B=70°,∠A=110°,
∴∠C=∠A=110°.
故答案为:110.
12.
【分析】根据矩形的性质即可得到结论.
【解答】解:∵四边形AOBC是矩形,
∴AC=OB=1,BC=OA=2,∠CAO=∠CBO=90°,
∴C的坐标为(﹣2,1),
故答案为:(﹣2,1).
13.
【分析】分别从当点F在C的左侧时与当点F在C的右侧时去分析,由当AE=CF时,以A、C、E、F为顶点四边形是平行四边形,可得方程,解方程即可求得答案.
【解答】解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2或6s时,以A、C、E、F为顶点四边形是平行四边形.
故答案为:2或6.
14.
【分析】根据平行四边形的性质可得AD∥BC,根据两直线平行内错角相等可得∠AFB=∠FBC,再由角平分线的定义可得∠ABF=∠FBC,从而不难推出∠AFB=∠ABF,由等角对等边可得AB=AF,已知AE的长,从而EF的长不难求解.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
∴∠AFB=∠ABF,
∴AB=AF;
∵AB=12,AE=5,
∴EF=AF﹣AE=12﹣5=7,
故答案为:7.
15.
【分析】先证∠BOM=∠CON,再证△BOM和△CON全等,得出△BOM和△CON的面积相等,再证得四边形OMCN的面积与△BOC的面积相等,即可得出答案.
【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD,∠OBM=∠OCN=45°,
∴∠BOC=90°,
∴∠BOM+∠COM=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON+∠COM=90°,
∴∠BOM=∠CON,
在△BOM和△CON中,
,
∴△BOM≌△CON(ASA),
∴S△BOM=S△CON,
∴S四边形OMCN=S△COM+S△CON=S△COM+S△BOM=S△BOC1,
故答案为:1.
16.
【分析】分别延长AC、BD交于点H,过G作MN∥AB,分别交AH于M,BH于N,易证四边形CPDH为平行四边形,得出G为PH中点,则G的运行轨迹△HAB的中位线MN,运用中位线的性质求出MN的长度即可.
【解答】解:如图,分别延长AC、BD交于点H,过G作MN∥AB,分别交AH于M,BH于N,
∵△APC和△BPD是等边三角形,
∴∠A=∠B=60°,
∴△AHB是等边三角形,
∵∠A=∠DPB=60°,
∴AH∥PD,
∵∠B=∠CPA=60°,
∴BH∥PC,
∴四边形CPDH为平行四边形,
∴CD与HP互相平分.
∵G为CD的中点,
∴G正好为PH中点,
∵△ABH是等边三角形,
∴在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.
∴MNAB=5,即G的移动路径长为5.
故答案为:5.
17.
【分析】先证明ADEF、BCEF是矩形,即可得到N是FC的中点,然后根据等腰直角三角形的三线合一得到∠AFE=90°,,然后求出CG长,即可得到CM长,再根据解题即可.
【解答】解:连接FC,
由条件可知∠D=90°,∠BAC=∠DAC=45°,AF∥CD,
∴ADEF、BCEF是矩形,
∴AF=DE=1,BF=3,∠AFE=90°,
又∵N是BE的中点,
∴F、C、N共线,且N是FC的中点,
由条件可知FA=FC=1,
∴,
又∵点M是AG的中点,
∴∠AMF=90°,,
又∵,
∴,
∴,
又∵N是FC的中点,
∴,
故答案为:90,.
18.
【分析】根据题意,在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动,当A′C取最小值时,由两点之间线段最短知此时M、A′、C三点共线,得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.
【解答】解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FDMD,
∴FM=DM×cos30°,
∴MC,
∴A′C=MC﹣MA′1.
故答案为:1.
三.解答题
19.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接BD交AC于O.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OCAC6=3,
∵AB=5,AO=3,
∴BO4,
∴BD=2BO=8,
∴S平行四边形ABCDAC×BD=24.
20.解:(1)如图,△A1B1C1即为所求.
(2)连接AA2,BB2,分别作线段AA2,BB2的垂直平分线,相交于点P,
则将△ABC绕点P逆时针旋转90°得到△A2B2C2,
由图可得,点P的坐标为(1,1).
故选:C.
21.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
22.(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BDAC,
∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DFAC,
∴BD=DF;
(2)证明:∵BD=DF,
∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,
解得:x=5,
∴四边形BDFG的周长=4GF=20.
23.(1)解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠C=90°,AB=CB,
作FP⊥CB于P,连接BE,
则四边形AFPB是矩形,
∴∠BCE=∠FPG=90°,
由翻折知,GF⊥BE,
∴∠PFG=∠CBE,
∵AB=CB=FP,
∴△FPG≌△BCE(ASA),
∴BE=FG=41,
在Rt△CBE中,由勾股定理得CE9,
故答案为:9;
(2)证明:如图2,连接FA,FP,FC,
∵正方形ABCD是轴对称图形,F为对角线BD上一点,
∴FA=FC,
又∵FE垂直平分AP,
∴FA=FP,
∴FP=FC,
∴∠FPC=∠FCP,
∵∠FAB=∠FCP,
∴∠FAB=∠FPC,
∴∠FAB+∠FPB=180°,
∴∠ABC+∠AFP=180°,
∴∠AFP=90°,
∴FEAP,
由【模型呈现】知,AP=MN,
∴MN=ME+EF+FN=AP=2EF,
∴EF=ME+FN;
(3)解:根据题意补全图形如图所示:
连接MG并延长使得MG=GH,
∵点G为BN的中点,
∴BG=NG,
又∵∠BGH=∠NGM,
∴△BGH≌△NGM(SAS),
∴HG=MG,BH=NM,∠BHG=∠NMG,则BH∥NM,
∴∠CBH=∠BFE,
∵四边形ABCD是正方形,
∴AD∥BC,∠ADC=90°,
∴∠BFE=∠DEM,∠CDM+∠EDM=90°,
又∵DM⊥EF,
∴∠DEM+∠EDM=90°,
∴∠CDM=∠DEM,
∴∠CDM=∠BFE,
∴∠CBH=∠CDM,
∵MN=DM,
∴BH=DM,
由正方形的性质可知,CB=CD,
∴△CBH≌△CDM(SAS),
∴CH=CM,∠BCH=∠DCM,∠BCD=90°,
则∠BCH+∠BCM=∠DCM+∠BCM=∠BCD=90°,
∴△MCH是等腰直角三角形,
∵HG=MG,
∴CG⊥MH,则△CGM也是等腰直角三角形,则CG=MG,
∴CMCG=2.
故答案为:2.
24.(1)证明:∵四边形形OABC是矩形,
∴OC∥AB,
∴∠COB=∠OBA,∠OPE=∠PEB,
∵D为OB中点,
∴OD=BD,
∴△OPD≌△BED(AAS),
∴OP=BE,
又∵OC∥AB,即OP∥BE,
∴四边形OPBE为平行四边形;
(2)解:∵O(0,0),B(6,8),
∴OB中点D坐标为(3,4),
设P(0,t),则OP=t,
∴S△OPDt 3,
设PD的直线表达式为y=kx+t,
∵D在PD上,
∴4=3k+t,
∴k,
∴PD:y.
令x=6,则y=﹣t+8,
∴E(6,8﹣t).
∴S四边形OAED=S△AED+S△ODA(8﹣t)+1224.
∵S△OPD:S四边形OAED=1:3,
∴24=3,
解得:t=4,
∴P(0,4).
(3)解:Q的坐标为(3,9)或(﹣3,4)或(3,).
如图,以OD为边,四边形ODQP为菱形,
∵D(3,4),
∴OD5,
∴Q(3,9);
如图,以OD为边,四边形ODPQ为菱形,
∴点D与点Q关于y轴对称,
∴Q(﹣3,4);
如图,以OD为对角线,四边形OQDP为菱形,延长DQ交x轴于点H,则QH⊥x轴,
设OQ=DQ=m,则QH=4﹣m,
∴32+(4﹣m)2=m2,
∴m,
∴DQ,
∴QH=4,
∴Q(3,).
综上所述,Q的坐标为(3,9)或(﹣3,4)或(3,).
25.解:(1)∵A(3,4),
∴AO5,
∵四边形AOBC为菱形,
∴AO=AB=5,AB∥OC,
∴点B坐标为(8,4),
故答案为:(8,4);
(2)∵B(5,1)、D(﹣3,﹣1)关于点P对称,
1,0,
∴点P的坐标为(1,0).
设点C(x,y),
∵A(3,3),
∴1,0,
∴x=﹣1,y=﹣3.
∴C(﹣1,﹣3).
故答案为:(﹣1,﹣3);
(3)当AB平行且等于NM时,四边形ABMN是平行四边形,
∵A(﹣1,2),N在y轴上,
∴M的横坐标为﹣5+1=﹣4;
当AB平行且等于NM时,四边形ABNM是平行四边形,
∵B(﹣5,1),N在y轴上,
∴M的横坐标为﹣1+5=4;
当AB为对角线时,四边形ANBM是平行四边形,
∵A(﹣1,2),B(﹣5,1),
∴M的横坐标为﹣1﹣5=﹣6;
故符合题意的有3个点,点M的横坐标分别为﹣4,4,﹣6.
故答案为:﹣4或4或﹣6;
(4)解题思路是:
①以点B为坐标原点,建立平面直角坐标系;
②求点P的坐标;
③由勾股定理可求AP的长.
一.选择题(共10小题,满分30分,每小题3分)
1.为培养学生利用现代信息技术解决数学问题的能力,十堰经开区数学教研室在本学期组织辖区内初中生开展了“运用几何画板,探寻美丽的数学世界”比赛活动.下列图形是部分参赛作品,是中心对称图形的是( )
A. B.
C. D.
2.如图,△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,点A、C的对应点分别为D、E,延长CA交DE于点F,下列结论错误的是( )
A.∠BED=30° B.∠DBE=45° C.∠ABD=60° D.∠CBE=60°
3.下列说法中不正确的是( )
A.四边相等的四边形是菱形
B.对角线垂直的平行四边形是菱形
C.菱形的对角线互相垂直且相等
D.菱形的邻边相等
4.如图,在Rt△ABC中,∠ACB=90°,CF是AB边上的中线,DE是△ABC的中位线,若CF=6,则DE的长( )
A.3 B.4 C.5 D.6
5.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若,BD=3,则菱形ABCD的面积为( )
A. B. C. D.
6.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )
A. B. C. D.
7.如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )
A.②③ B.②⑤ C.①③④ D.④⑤
8.如图,已知点P是矩形ABCD内一点(不含边界),设∠PAD=θ1,∠PBA=θ2,∠PCB=θ3,∠PDC=θ4,若∠APB=80°,∠CPD=50°,则( )
A.(θ1+θ4)﹣(θ2+θ3)=30°
B.(θ2+θ4)﹣(θ1+θ3)=40°
C.(θ1+θ2)﹣(θ3+θ4)=70°
D.(θ1+θ2)+(θ3+θ4)=180°
9.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为( )
A. B.2 C.2 D.4
10.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共8小题,满分24分,每小题3分)
11.已知在 ABCD中,∠A比∠B大40°,那么∠C的度数是 .
12.如图,长方形AOBC中,A、B在坐标轴上,OA=2,OB=1,则C的坐标为 .
13.如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t= s时,以A、C、E、F为顶点四边形是平行四边形.
14.如图,已知平行四边形ABCD中,∠BCD的平分线交边AD于E,∠ABC的平分线交AD于F,若AB=12,AE=5,则EF= .
15.如图,正方形ABCD的对角线AC,BD相交于点O,点M是BC边上一点,连接OM,过点O作ON⊥OM,交CD于点N,若正方形ABCD的边长为2,则四边形OMCN的面积是 .
16.如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是 .
17.如图,四边形ABCD是边长为4的正方形,点E在边CD上,DE=1,作EF∥BC,分别与边AB、AC交于点F、G,点M,N分别是AG,BE的中点,则∠FMA= °,△MNC的面积是 .
18.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
三.解答题(共7小题,满分66分)
19.(8分)如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
20.(6分)如图所示的正方形网格中,每个小正方形的边长为1,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)作出△ABC关于坐标原点O成中心对称的△A1B1C1;
(2)若将△ABC绕点P旋转得到△A2B2C2,则点P的坐标为 .
A.(0,1)
B.(1,2)
C.(1,1)
D.(1,0)
21.(8分)如图,四边形ABCD是平行四边形,E为AB上一点.
(1)如图①,只用无刻度直尺在CD上作出点F,使得四边形AECF为平行四边形;
(2)如图②,用直尺和圆规作出矩形EFGH,使得点F、G、H分别在BC、CD、DA上.(保留作图痕迹,写出必要的文字说明)
22.(8分)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:BD=DF;
(2)求证:四边形BDFG为菱形;
(3)若AG=13,CF=6,求四边形BDFG的周长.
23.(12分)【模型呈现】在正方形学习过程中,我们发现下面的结论:如图1,正方形ABCD中,点P为线段BC上一个动点,若线段MN垂直AP于点E,交线段AB于点M,交线段CD于点N,则AP=MN.
(1)如图②,将边长为40的正方形ABCD折叠,使得点B落在CD上的点E处.若折痕FG=41,则CE= .
【继续探索】
(2)如图③,正方形ABCD中,点P为线段BC上一动点,若MN垂直平分线段AP,分别交AB,AP,BD,
DC于点M,E,F,N.求证:EF=ME+FN.
(3)如图④,在正方形ABCD中,E、F分别为AD,BC上的点,作DM⊥EF于M,在MF上截取MN=DM,
连接BN,G为BN中点,连接CG,CM.请依题意补全图形,若CG=2,则CM= .
24.(12分)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(6,8),点D为对角线OB的中点.点P是OC边上一动点,直线PD交AB边于点E.
(1)求证:四边形OPBE为平行四边形;
(2)若△ODP的面积与四边形OAED的面积之比为1:3,求点P的坐标;
(3)设点Q是x轴上方平面内的一点,以点O、D、P、Q为顶点的四边形是菱形,直接写出点Q的坐标.
25.(12分)平面直角坐标系不仅可以研究函数,还可以研究并解决很多图形以及图形变换问题.
(1)如图①,在菱形OABC中,若点A(3,4),则点B坐标为 ;
(2)如图②,线段AB、CD关于点P对称,若点A(3,3)、B(5,1)、D(﹣3,﹣1),则点C的坐标为 ;
(3)如图③,在直角坐标系中,点A、B的坐标分别为(﹣1,2)、(﹣5,1),点M、N分别是x轴、y轴上的点,若以点A、B、M、N为顶点的四边形是平行四边形,则点M的横坐标为 ;
(4)如图④,已知正方形ABCD的边长为5,E、F分别是边CD、AD上的点,BE、CF交于点P,CE=DF=2,写出求AP长的解题思路.
参考答案
一.选择题
1.
【分析】把一个图形绕某一点旋转180°后,能够与原图形重合,那么这个图形就叫做中心对称图形,据此分析判断即可.
【解答】解:中心对称图形的概念逐项分析判断如下:
A、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
B、绕某一点旋转180°后,能够与原图形重合,是中心对称图形,故符合题意;
C、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
D、绕某一点旋转180°后,不能够与原图形重合,不是中心对称图形,故不符合题意;
故选:B.
2.
【分析】直接根据旋转的性质逐一判断即可.
【解答】解:∵△ABC中,∠ABC=45°,将△ABC绕点B逆时针旋转60°得到△DBE,
∴∠DBE=∠ABC=45°,∠ABD=∠CBE=60°,
故选项B、C、D正确,
由已知条件无法得出∠BED=30°,
故选项A错误,
故选:A.
3.
【分析】由菱形的判定与性质即可得出A、B、D正确,C不正确.
【解答】解:A.四边相等的四边形是菱形;正确;
B.对角线垂直的平行四边形是菱形;正确;
C.∵菱形的对角线互相垂直且平分,
∴选项C不正确;
D.菱形的邻边相等;正确;
故选:C.
4.
【分析】根据直角三角形斜边上的直线的性质得出AB的长,再根据三角形中位线定理得出结果.
【解答】解:在Rt△ABC中,∠ACB=90°,CF是AB边上的中线,
∴AB=2CF=12,
∵DE是△ABC的中位线,
∴DE6,
故选:D.
5.
【分析】首先根据三角形中位线定理得到,再计算菱形的面积即可.
【解答】解:∵E,F分别是AD,CD边上的中点,,
∴,
∵四边形ABCD是菱形,
∴菱形ABCD的面积,
故选:C.
6.
【分析】依据矩形的性质即可得到△AOD的面积为12,再根据S△AOD=S△AOE+S△DOE,即可得到OE+EF的值.
【解答】解:∵AB=6,BC=8,
∴矩形ABCD的面积为48,AC10,
∴AO=DOAC=5,
∵对角线AC,BD交于点O,
∴△AOD的面积为12,
∵EO⊥AO,EF⊥DO,
∴S△AOD=S△AOE+S△DOE,即12AO×EODO×EF,
∴125×EO5×EF,
∴5(EO+EF)=24,
∴EO+EF,
故选:C.
7.
【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得MNAB,从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;确定出点P到MN的距离不变,然后根据等底等高的三角形的面积相等确定出③不变;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
【解答】解:∵点A,B为定点,点M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MNAB,
即线段MN的长度不变,故①错误;
PA、PB的长度随点P的移动而变化,
所以,△PAB的周长会随点P的移动而变化,故②正确;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故③错误;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小点P的移动而变化,故⑤正确.
综上所述,会随点P的移动而变化的是②⑤.
故选:B.
8.
【分析】依据矩形的性质以及三角形内角和定理,可得θ2﹣θ1=10°,θ4﹣θ3=40°,两式相减即可得到(θ1+θ4)﹣(θ2+θ3)=30°.
【解答】解:∵矩形ABCD,
∴∠BAD=∠BCD=90°,
∴∠BAP=90°﹣θ1,∠DCP=90°﹣θ3,
∴△ABP中,90°﹣θ1+θ2+80°=180°,即θ2﹣θ1=10°,①
△DCP中,90°﹣θ3+θ4+50°=180°,即θ4﹣θ3=40°,②
由②﹣①,可得(θ4﹣θ3)﹣(θ2﹣θ1)=30°,
即(θ1+θ4)﹣(θ2+θ3)=30°,
故选:A.
9.
【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.
【解答】解:如图,连接AE,
∵四边形DEFG是正方形,
∴∠EDG=90°,EF=DE=DG,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE=∠CDG,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴d1+d2+d3=EF+CF+AE,
∴点A,E,F,C在同一条线上时,EF+CF+AE最小,即d1+d2+d3最小,
连接AC,
∴d1+d2+d3最小值为AC,
在Rt△ABC中,ACAB=2,
∴d1+d2+d3最小=AC=2,
故选:C.
10.
【分析】①利用线段垂直平分线的性质的逆定理可得结论;
②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;
③可证明∠CDE=∠DFE;
④可通过面积转化进行解答.
【解答】解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,FO=FC,
∴BO⊥EF,BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠CBF=30°,∠BEO=60°,
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∴S△AOE:S△BCM=2S△CMF:S△BCM,
∵∠FCO=30°,
∴FM,BMCM,
∴,
∴S△AOE:S△BCM=2:3,
故④正确;
所以其中正确结论的个数为3个;
故选:B.
二.填空题
11.
【分析】根据平行四边形的对角相等,邻角之和为180°,即可求出该平行四边形各个内角的度数.
【解答】解:∵四边形ABCD是平行四边形,
∴∠B=∠D,∠A+∠B=180°,
又∵∠A﹣∠B=40°,
∴∠B=70°,∠A=110°,
∴∠C=∠A=110°.
故答案为:110.
12.
【分析】根据矩形的性质即可得到结论.
【解答】解:∵四边形AOBC是矩形,
∴AC=OB=1,BC=OA=2,∠CAO=∠CBO=90°,
∴C的坐标为(﹣2,1),
故答案为:(﹣2,1).
13.
【分析】分别从当点F在C的左侧时与当点F在C的右侧时去分析,由当AE=CF时,以A、C、E、F为顶点四边形是平行四边形,可得方程,解方程即可求得答案.
【解答】解:①当点F在C的左侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BC﹣BF=6﹣2t(cm),
∵AG∥BC,
∴当AE=CF时,四边形AECF是平行四边形,
即t=6﹣2t,
解得:t=2;
②当点F在C的右侧时,根据题意得:AE=tcm,BF=2tcm,
则CF=BF﹣BC=2t﹣6(cm),
∵AG∥BC,
∴当AE=CF时,四边形AEFC是平行四边形,
即t=2t﹣6,
解得:t=6;
综上可得:当t=2或6s时,以A、C、E、F为顶点四边形是平行四边形.
故答案为:2或6.
14.
【分析】根据平行四边形的性质可得AD∥BC,根据两直线平行内错角相等可得∠AFB=∠FBC,再由角平分线的定义可得∠ABF=∠FBC,从而不难推出∠AFB=∠ABF,由等角对等边可得AB=AF,已知AE的长,从而EF的长不难求解.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
∴∠AFB=∠ABF,
∴AB=AF;
∵AB=12,AE=5,
∴EF=AF﹣AE=12﹣5=7,
故答案为:7.
15.
【分析】先证∠BOM=∠CON,再证△BOM和△CON全等,得出△BOM和△CON的面积相等,再证得四边形OMCN的面积与△BOC的面积相等,即可得出答案.
【解答】解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OC=OB=OD,∠OBM=∠OCN=45°,
∴∠BOC=90°,
∴∠BOM+∠COM=90°,
∵ON⊥OM,
∴∠MON=90°,
∴∠CON+∠COM=90°,
∴∠BOM=∠CON,
在△BOM和△CON中,
,
∴△BOM≌△CON(ASA),
∴S△BOM=S△CON,
∴S四边形OMCN=S△COM+S△CON=S△COM+S△BOM=S△BOC1,
故答案为:1.
16.
【分析】分别延长AC、BD交于点H,过G作MN∥AB,分别交AH于M,BH于N,易证四边形CPDH为平行四边形,得出G为PH中点,则G的运行轨迹△HAB的中位线MN,运用中位线的性质求出MN的长度即可.
【解答】解:如图,分别延长AC、BD交于点H,过G作MN∥AB,分别交AH于M,BH于N,
∵△APC和△BPD是等边三角形,
∴∠A=∠B=60°,
∴△AHB是等边三角形,
∵∠A=∠DPB=60°,
∴AH∥PD,
∵∠B=∠CPA=60°,
∴BH∥PC,
∴四边形CPDH为平行四边形,
∴CD与HP互相平分.
∵G为CD的中点,
∴G正好为PH中点,
∵△ABH是等边三角形,
∴在P的运动过程中,G始终为PH的中点,所以G的运行轨迹为△HAB的中位线MN.
∴MNAB=5,即G的移动路径长为5.
故答案为:5.
17.
【分析】先证明ADEF、BCEF是矩形,即可得到N是FC的中点,然后根据等腰直角三角形的三线合一得到∠AFE=90°,,然后求出CG长,即可得到CM长,再根据解题即可.
【解答】解:连接FC,
由条件可知∠D=90°,∠BAC=∠DAC=45°,AF∥CD,
∴ADEF、BCEF是矩形,
∴AF=DE=1,BF=3,∠AFE=90°,
又∵N是BE的中点,
∴F、C、N共线,且N是FC的中点,
由条件可知FA=FC=1,
∴,
又∵点M是AG的中点,
∴∠AMF=90°,,
又∵,
∴,
∴,
又∵N是FC的中点,
∴,
故答案为:90,.
18.
【分析】根据题意,在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动,当A′C取最小值时,由两点之间线段最短知此时M、A′、C三点共线,得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.
【解答】解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FDMD,
∴FM=DM×cos30°,
∴MC,
∴A′C=MC﹣MA′1.
故答案为:1.
三.解答题
19.(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD
∴AB=AD,
∴四边形ABCD是菱形.
(2)连接BD交AC于O.
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OCAC6=3,
∵AB=5,AO=3,
∴BO4,
∴BD=2BO=8,
∴S平行四边形ABCDAC×BD=24.
20.解:(1)如图,△A1B1C1即为所求.
(2)连接AA2,BB2,分别作线段AA2,BB2的垂直平分线,相交于点P,
则将△ABC绕点P逆时针旋转90°得到△A2B2C2,
由图可得,点P的坐标为(1,1).
故选:C.
21.解:(1)如图1,点F,四边形AECF即为所求作.
(2)如图2,四边形EFGH即为所求作.
理由:由△AOE≌△COF,可得OE=OF,
由△AOH≌△COF.可得OH=OF,
∴四边形EFGH是平行四边形,
∵OG=OF,
∴FH=EG,
∴四边形EFGH是矩形.
22.(1)证明:∵∠ABC=90°,BD为AC的中线,
∴BDAC,
∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴DFAC,
∴BD=DF;
(2)证明:∵BD=DF,
∴四边形BGFD是菱形,
(3)解:设GF=x,则AF=13﹣x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,
解得:x=5,
∴四边形BDFG的周长=4GF=20.
23.(1)解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠C=90°,AB=CB,
作FP⊥CB于P,连接BE,
则四边形AFPB是矩形,
∴∠BCE=∠FPG=90°,
由翻折知,GF⊥BE,
∴∠PFG=∠CBE,
∵AB=CB=FP,
∴△FPG≌△BCE(ASA),
∴BE=FG=41,
在Rt△CBE中,由勾股定理得CE9,
故答案为:9;
(2)证明:如图2,连接FA,FP,FC,
∵正方形ABCD是轴对称图形,F为对角线BD上一点,
∴FA=FC,
又∵FE垂直平分AP,
∴FA=FP,
∴FP=FC,
∴∠FPC=∠FCP,
∵∠FAB=∠FCP,
∴∠FAB=∠FPC,
∴∠FAB+∠FPB=180°,
∴∠ABC+∠AFP=180°,
∴∠AFP=90°,
∴FEAP,
由【模型呈现】知,AP=MN,
∴MN=ME+EF+FN=AP=2EF,
∴EF=ME+FN;
(3)解:根据题意补全图形如图所示:
连接MG并延长使得MG=GH,
∵点G为BN的中点,
∴BG=NG,
又∵∠BGH=∠NGM,
∴△BGH≌△NGM(SAS),
∴HG=MG,BH=NM,∠BHG=∠NMG,则BH∥NM,
∴∠CBH=∠BFE,
∵四边形ABCD是正方形,
∴AD∥BC,∠ADC=90°,
∴∠BFE=∠DEM,∠CDM+∠EDM=90°,
又∵DM⊥EF,
∴∠DEM+∠EDM=90°,
∴∠CDM=∠DEM,
∴∠CDM=∠BFE,
∴∠CBH=∠CDM,
∵MN=DM,
∴BH=DM,
由正方形的性质可知,CB=CD,
∴△CBH≌△CDM(SAS),
∴CH=CM,∠BCH=∠DCM,∠BCD=90°,
则∠BCH+∠BCM=∠DCM+∠BCM=∠BCD=90°,
∴△MCH是等腰直角三角形,
∵HG=MG,
∴CG⊥MH,则△CGM也是等腰直角三角形,则CG=MG,
∴CMCG=2.
故答案为:2.
24.(1)证明:∵四边形形OABC是矩形,
∴OC∥AB,
∴∠COB=∠OBA,∠OPE=∠PEB,
∵D为OB中点,
∴OD=BD,
∴△OPD≌△BED(AAS),
∴OP=BE,
又∵OC∥AB,即OP∥BE,
∴四边形OPBE为平行四边形;
(2)解:∵O(0,0),B(6,8),
∴OB中点D坐标为(3,4),
设P(0,t),则OP=t,
∴S△OPDt 3,
设PD的直线表达式为y=kx+t,
∵D在PD上,
∴4=3k+t,
∴k,
∴PD:y.
令x=6,则y=﹣t+8,
∴E(6,8﹣t).
∴S四边形OAED=S△AED+S△ODA(8﹣t)+1224.
∵S△OPD:S四边形OAED=1:3,
∴24=3,
解得:t=4,
∴P(0,4).
(3)解:Q的坐标为(3,9)或(﹣3,4)或(3,).
如图,以OD为边,四边形ODQP为菱形,
∵D(3,4),
∴OD5,
∴Q(3,9);
如图,以OD为边,四边形ODPQ为菱形,
∴点D与点Q关于y轴对称,
∴Q(﹣3,4);
如图,以OD为对角线,四边形OQDP为菱形,延长DQ交x轴于点H,则QH⊥x轴,
设OQ=DQ=m,则QH=4﹣m,
∴32+(4﹣m)2=m2,
∴m,
∴DQ,
∴QH=4,
∴Q(3,).
综上所述,Q的坐标为(3,9)或(﹣3,4)或(3,).
25.解:(1)∵A(3,4),
∴AO5,
∵四边形AOBC为菱形,
∴AO=AB=5,AB∥OC,
∴点B坐标为(8,4),
故答案为:(8,4);
(2)∵B(5,1)、D(﹣3,﹣1)关于点P对称,
1,0,
∴点P的坐标为(1,0).
设点C(x,y),
∵A(3,3),
∴1,0,
∴x=﹣1,y=﹣3.
∴C(﹣1,﹣3).
故答案为:(﹣1,﹣3);
(3)当AB平行且等于NM时,四边形ABMN是平行四边形,
∵A(﹣1,2),N在y轴上,
∴M的横坐标为﹣5+1=﹣4;
当AB平行且等于NM时,四边形ABNM是平行四边形,
∵B(﹣5,1),N在y轴上,
∴M的横坐标为﹣1+5=4;
当AB为对角线时,四边形ANBM是平行四边形,
∵A(﹣1,2),B(﹣5,1),
∴M的横坐标为﹣1﹣5=﹣6;
故符合题意的有3个点,点M的横坐标分别为﹣4,4,﹣6.
故答案为:﹣4或4或﹣6;
(4)解题思路是:
①以点B为坐标原点,建立平面直角坐标系;
②求点P的坐标;
③由勾股定理可求AP的长.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
