27.2.3 相似三角形应用举例复习题-2024-2025学年九年级数学下册人教版(含解析)
文档属性
| 名称 | 27.2.3 相似三角形应用举例复习题-2024-2025学年九年级数学下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 09:17:22 | ||
图片预览



文档简介
27.2.3 相似三角形应用举例复习题
【题型1 建筑物高问题】
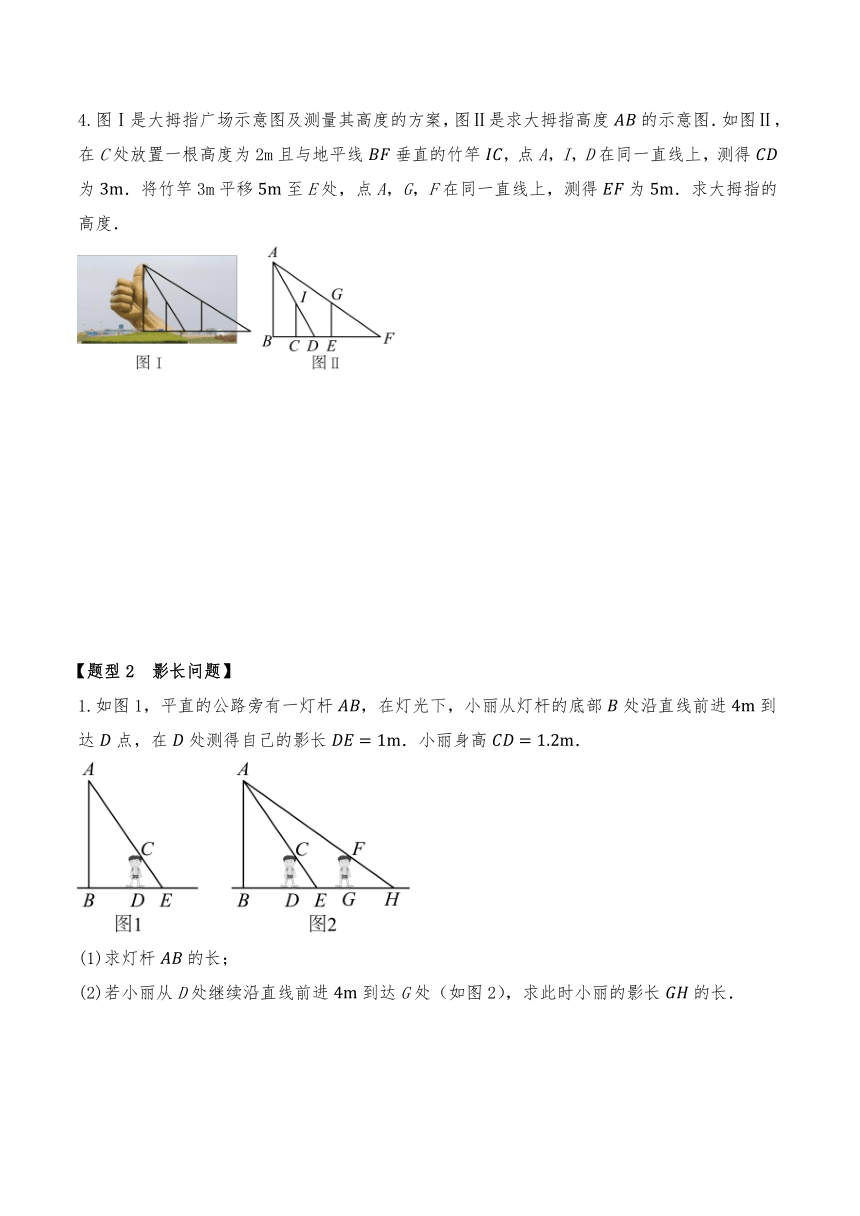
1.小亮运用《数书九章》中测量塔高的方法测量一幢楼房的高度.如图,表示楼房的高,表示一根直杆顶端到地面的高,表示小亮的眼睛到地面的高,在同一平面内,点在同一条直线上.已知,,,,小亮从点远眺楼顶,视线恰好经过直杆的顶端,请帮小亮求出楼房的高.
2.圭表是中国古代根据日影长度变化测定季节、划分四季和推算历法的工具.图1为圭表示意图.某同学受到启发,利用一根标杆和一个卷尺轻松测量出学校旗杆的高度.如图2,旗杆的影长在水平地面上,将标杆(长度1米)竖直放置在影长的最远端点A处,此时标杆的影长为.经测量,米,米.
(1)根据以上信息,计算旗杆的高度.(结果保留整数)
(2)若该同学在操作过程中,测量完的长度后,准备测量的长度时,发现卷尺不够长,又去寻找更长一点的卷尺,半小时后回来测量的长度,请问这样可以准确得到旗杆的高度吗?简单说明理由.
3.小明和小亮两位同学春节期间在游览某景区时,对景区内一座古塔产生浓厚的兴趣,他们想用所学的知识测量古塔的高度.为了保护古塔,工作人员在古塔底部设有栅栏,古塔底部不可直接到达.经询问得知栅栏长17米(即米),小亮在F处利用1米高的栅栏(即米,且),在栅栏顶端G处测得塔的顶部A处的仰角为,小明同学在古塔另一侧的C处放置平面镜(点D,C,B,F四点在一条直线上),当他站在D处时恰好能从平面镜中看到古塔的塔顶A,已知小明的身高为米(即米,且),小明到平面镜的水平距离为米(即米),求古塔的高.
4.图Ⅰ是大拇指广场示意图及测量其高度的方案,图Ⅱ是求大拇指高度的示意图.如图Ⅱ,在C处放置一根高度为2m且与地平线垂直的竹竿,点A,I,D在同一直线上,测得为.将竹竿3m平移至E处,点A,G,F在同一直线上,测得为.求大拇指的高度.
【题型2 影长问题】
1.如图1,平直的公路旁有一灯杆,在灯光下,小丽从灯杆的底部处沿直线前进到达点,在处测得自己的影长.小丽身高.
(1)求灯杆的长;
(2)若小丽从D处继续沿直线前进到达G处(如图2),求此时小丽的影长的长.
2.操场上有一根竖直的旗杆,它的一部分影子()落在水平地面上,另一部分影子()落在对面的墙壁上,经测量,墙壁上的影高为,地面的影长为,同时测得一根高为的竹竿的影长是,请根据以上信息,则旗杆的高度是( )
A. B. C. D.
3.如图,在路灯下,表示小明的身高,表示他的影子,表示小亮的身高,路灯灯泡在线段上.
(1)请你画出灯泡的位置,并画出小亮在灯光下的影子;
(2)如果小明的身高,他的影子,且他到路灯的距离,求路灯的高.
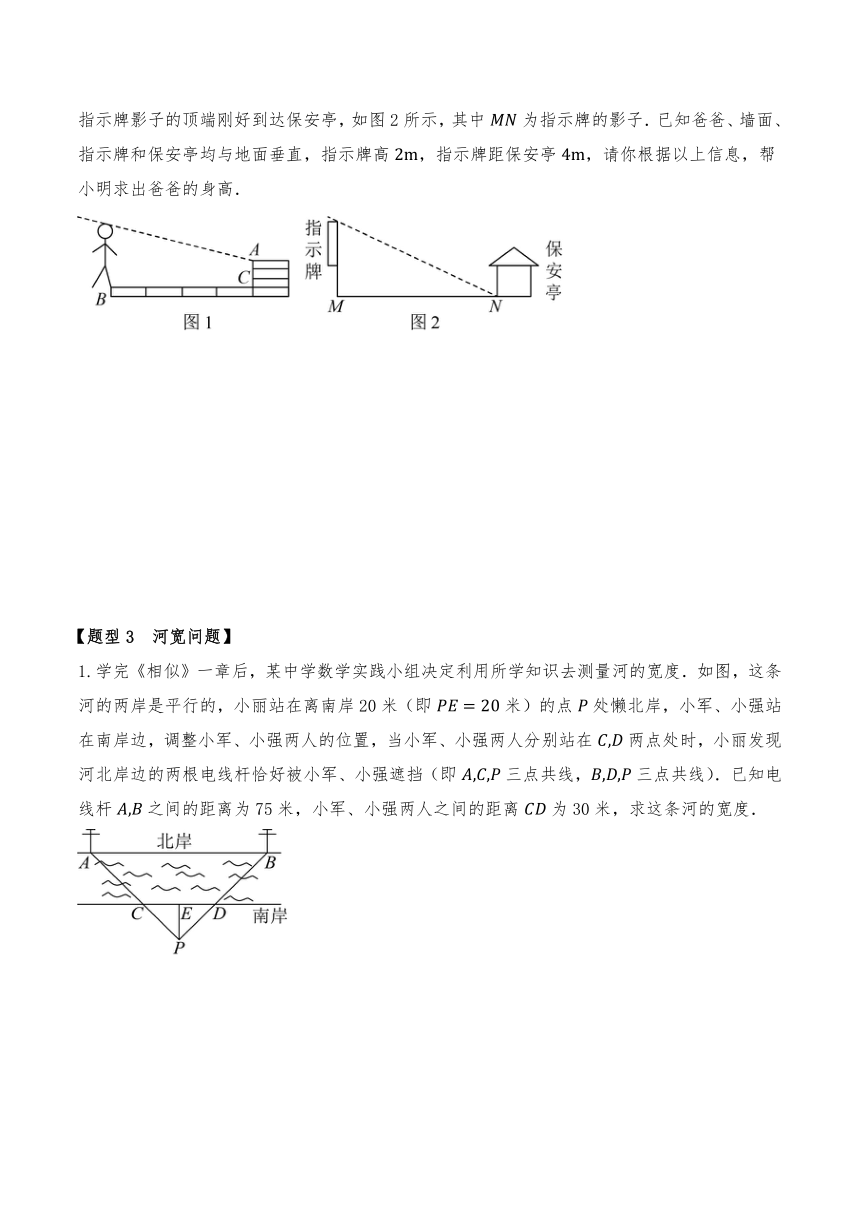
4.小明和爸爸在公园散步,此时爸爸的影子落在了身后的地面和墙上,如图1所示.其中,段为地上的影子,段为墙上的影子.小明想利用所学知识测量出爸爸的身高.他向工作人员询问得知:公园地面与墙面所用均为厚度,长度的砖块,小明数了一下,段刚好是4块地砖的长度,而段恰好为4块地砖的厚度;同一时刻,小明观察到公园门口指示牌影子的顶端刚好到达保安亭,如图2所示,其中为指示牌的影子.已知爸爸、墙面、指示牌和保安亭均与地面垂直,指示牌高,指示牌距保安亭,请你根据以上信息,帮小明求出爸爸的身高.
【题型3 河宽问题】
1.学完《相似》一章后,某中学数学实践小组决定利用所学知识去测量河的宽度.如图,这条河的两岸是平行的,小丽站在离南岸20米(即米)的点处懒北岸,小军、小强站在南岸边,调整小军、小强两人的位置,当小军、小强两人分别站在两点处时,小丽发现河北岸边的两根电线杆恰好被小军、小强遮挡(即三点共线,三点共线).已知电线杆之间的距离为75米,小军、小强两人之间的距离为30米,求这条河的宽度.
2.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
3.如图,为了测量某河段的宽度,某校数学课外活动小组在河对岸选定一个目标点A,在近岸取点B和C,使点A、B、C共线且直线AB与河岸b垂直,接着在过点C且与AB垂直的直线a上选择适当的点D,点A、D与河岸b上的点E在一条直线上.测得,,,请根据这些数据,计算河宽AB.
4.如图,为了测量平静的河面的宽度,即的长,在离河岸点米远的点,立一根长为米的标杆,在河对岸的岸边有一根长为米的电线杆,电线杆的顶端在河里的倒影为点,即,两岸均高出水平面米,即米,经测量此时、、三点在同一直线上,并且点、、、共线,点、、共线,若、、均垂直于河面,求河宽是多少米?
【题型4 树高问题】
1.《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
2.如图,直立在B处的标杆AB=2.9米,小爱站在F处,眼睛E处看到标杆顶A,树顶C在同一条直线上(人,标杆和树在同一平面内,且点F,B,D在同一条直线上).已知BD=6米,FB=2米,EF=1.7米,求树高CD.
3.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得;再在BD的延长线上确定一点G,使米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得米,小明眼睛与地面的距离米,测量器的高度米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(小平面镜的大小忽略不计)
4.小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他利用镜子进行两次测量,如图,第一次他把镜子放在点处,他在点处正好在镜中看到树尖的像;第二次他把镜子放在点处,他在点处正好在镜中看到树尖的像.已知,,,小军的眼睛距地面(即),量得,求这棵古松树的高度.(镜子大小忽略不计)
【题型5 杠杆问题】
1.阿基米德曾说过:“给我一个支点和一根足够长的杆子,我就能撬起整个地球.”这句话的意思是利用物理学中的杠杆原理,只要有合适的支点和合适的工具,就可以把地球轻松搬动.如图1,这是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图2中,杠杆的D端被向上翘起的距离,动力臂与阻力臂满足(与相交于点O),则的长为 cm.
2.如图,是一个杠杆,可绕支点自由转动,当处于图中的位置时,点到点的水平距离,点到点的水平距离,若已知杠杆的段长为2.5,则杠杆的段长为 .
3.如图是用杠杆撬石头的示意图,点C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起,已知,要使这块石头滚动,至少要将杠杆的A端向下压 .
4.如图所示的是古代一种可以远程攻击的投石车,图是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点,重锤挂在点,点A为支点,点是水平底板上的一点,米,米.
(1)投石车准备时,点恰好与点重合,此时和垂直,则 米
(2)投石车投石过程中,的延长线交线段于点,若::,则点距地面为 米.
【题型6 实验问题】
1.如图,嘉嘉同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求的长.
(2)求灯泡到地面的高度.
2.约在两千五百年前,如图(1),墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图(2)所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是 .
3.如图,佳佳同学正在使用手电筒进行物理光学实验,水平地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,木板到平面镜的水平距离,已知光在镜面反射中的入射角等于反射角,求灯泡到地面的高度.
4.小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆水平放置,此时木杆在水平地面上的影子为线段.
①若木杆的长为,则其影子的长为___________;
②在同一时刻同一地点,将另一根木杆直立于地面,请画出表示此时木杆在地面上影子的线段:
(2)如图2,夜晚在路灯下,小桃将木杆水平放置,此时木杆在水平地面上的影子为线段.
①请在图中画出表示路灯灯泡位置的点;
②若木杆的长为,经测量木杆距离地面,其影子的长为,则路灯距离地面的高度为___________.
【题型7 古文问题】
1.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何?”它的意思是:如图,M,N分别是正方形的边,的中点,,,过点A,且步,步,那么该正方形城邑边长约为( )步.
A.300 B.250 C.225 D.150
2.《九章算术》是我国古代数学名著,书中有如下问题: “今有井径尺,不知其深,立五尺木于井上,从木末 望水岸,入径四寸.问井深几何?”意思是:如图, 井径尺,立木高尺,寸尺,则井深为 尺.
3.《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD,点E,G分别为CD,AD的中点,EF⊥CD,GH⊥AD,点F,D,H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( )
A.150步 B.200步 C.250步 D.300步
4.“度高者重表,测深者累矩,孤离者三望,离而又旁求者四望.触类而长之,则虽幽遐诡伏,靡所不入.”就是说,使用多次测量传递的方法,就可以测量出各点之间的距离和高度差.——刘徽《九章算术注·序》.某市科研考察队为了求出某海岛上的山峰的高度,如图,在同一海平面的处和处分别树立标杆和,标杆的高都是5.5米,两处相隔80米,从标杆向后退11米的处,可以看到顶峰和标杆顶端在一条直线上;从标杆向后退13米的处,可以看到顶峰和标杆顶端在一条直线上.求山峰的高度及它和标杆的水平距离.
注:图中各点都在一个平面内.
【题型8 裁剪问题】
1.有一等腰三角形纸片ABC,AB=AC,裁剪方式及相关数据如图所示,则得到的甲、乙、丙、丁四张纸片中,面积最大的是( )
A.甲 B.乙 C.丙 D.丁
2.三八妇女节,同学们准备送小礼物给妈妈,首先利用正方形纸板,制作一个正方体礼品盒(如图所示裁剪).已知正方形纸板边长为分米,则这个礼品盒的体积 立方分米.
3.在综合实践课中,小慧将一张长方形卡纸如图1所示裁剪开,无缝隙不重叠的拼成如图2所示的“”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知,,.
求(1)线段与的差值是___
(2)的长度.
4.一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分别为12cm和14cm.
(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
【题型9 现实生活相关问题】
1.如图是一个常见的铁夹的剖面图,,表示铁夹的剖面的两条边,点是转动轴的位置,,垂足为,,,,且铁夹的剖面图是轴对称图形,则,两点间的距离为( )
A. B. C. D.
2.如图,已知箱子沿着斜面向上运动,箱高.当时,点B到地面的距离,则点A到地面的距离为( )
A. B. C. D.
3.如图①,是生活中常见的人字梯,也称折梯,因其使用时,左右的梯杆及地面构成一个等腰三角形,因而把它形象的称为“人字梯”.如图②,是其工作示意图,拉杆米,则两梯杆跨度B、C之间距离为 米.
【题型10 三角形内接矩形问题】
1.有一块锐角三角形余料,边为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为的边在上,则按如图方式分割成的小长方形零件最多有 .
2.如图,有一块三角形余料ABC,它的边,高,现在要把它加工成长与宽的比为的矩形零件,要求一条长边在上,其余两个顶点分别在,上,则矩形的周长为 cm.
3.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图,是他研究的一个汽车盲区的示意图,为驾驶员的盲区,驾驶员的眼睛点处与地面的距离为,车宽,车头近似看成一个矩形,且满足,求汽车盲区的长度.
4.(1)【问题探究】如图①,点B,C分别在上,米,米,米,米,米.
①探究与是否相似并说明理由;
②求的长.
(2)【问题解决】如图②,四边形规划为园林绿化区,对角线将整个四边形分成面积相等的两部分,已知米,四边形的面积为平方米,为了更好地美化环境,政府计划在边上分别确定点E,F,在边上确定点P,Q,使四边形为矩形,在矩形内种植花卉,在四边形剩余区域种植草坪,为了方便市民观赏,计划在之间修一条小路,并使得最短,根据设计要求,求出的最小值,并求出当最小时,花卉种植区域的面积.
参考答案
【题型1 建筑物高问题】
1.解:过作于,交于E,
则,,,
,,
,
,
,
,
,
,
答:楼房的高为.
2.(1)解:由题意,可知.
∴.
又∵,
∴.
∴,即.
∴(米).
答:旗杆MN的高度约为10米.
(2)解:不可以.
理由如下:旗杆和标杆的影长随着时间变化而变化,必须同时测量,小明测量标杆影长后半个小时再测旗杆影长,此时旗杆影长已发生变化,故不可以准确得到旗杆的高度.(理由合理即可)
3.解:如图:过点G作,垂足为H,
由题意得:米,
设米,
∵米,
∴米,
在中,,
∴米,
∴米,
由题意得:,
∴,
∴,
∴,即:,解得:,
∴,解得:,
∴(米),
∴古塔的高为12米.
4.解:由题意可得:,
∴.
∴.
由题意可得:,
∴.
∴.
∵,
∴,即,解得:.
将代入,得.解得.
∴大拇指的高度为.
【题型2 影长问题】
1.(1)解:如图1,根据题意得:,(米,
,
,
即,
解得:(米;
答:灯杆的高度为;
(2)如图2,根据题意得:,(米,
,
,
即,
解得:(米;
答:此时小丽的影长的长是.
2.C
【分析】过点D作于点E,根据题意,,得到矩形,继而得到,根据同一时刻,物高与影长成正比,建立等式计算即可.
本题考查了矩形的判定和性质,相似三角形的应用,熟练掌握解矩形的应用是解题的关键.
【详解】过点D作于点E,根据题意,得,
∴四边形为矩形,
∴,
∵,,
∴,
根据同一时刻,物高与影长成正比,
∴即,
解得,
∴.
故选C.
3.(1)解:如图,
点O为灯泡的位置, FH为小亮在灯光下的影子;
(2)解:,
,
,
,
解得:,
路灯的高为.
4.解:如图:过点作,垂足为,
由题意得:,,
指示牌高,指示牌距保安亭,
,
,
,
爸爸的身高为.
【题型3 河宽问题】
1.解:延长交于点,如解图所示.
依题意,米,米.
设这条河的宽度为米.
,
.
,
即,
解得.
答:这条河的宽度为30米.
2.解:∵CB⊥AD,ED⊥AD,
∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,
∴ ABC∽ ADE,
∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,
∴,
∴AB=17,
即河宽为17m.
3.解:由题意得,,
∴,
∴,即.
∵,,,
∴ ,
解得 .
答:河宽AB大约是20m.
4.解:延长交的反向延长线于点,
则四边形是矩形,
,,
,
,
,
,
,
,
,米,米,
米,
,,
,
,
,
,
,
,
答:河宽是12米.
【题型4 树高问题】
1.解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
2.解:过E作EH⊥CD交CD于H点,交AB于点G,则EH⊥AB,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.7米,EG=FB=2米,GH=BD=6米,
∴AG=AB GB=2.9 1.7=1.2(米),
∵AG∥CH,
∴△AEG∽△CEH,
∴,
∴,
∴CH=4.8,
∴CD=CH+DH=4.8+1.7=6.5(米).
答:树高CD为6.5米.
3.如图,过点作于点,则,,
在 中,,
∴,
∴,
∵,,
∴
由反射角等于入射角得,
∴,
∴,即,
解得
∴
∴这棵树高18米.
4.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,,,
∴,
解得:,
∴,
解得:,
答:这棵古松树的高度为m.
【题型5 杠杆问题】
1.解:由题意得,,
,
,
,
,
cm.
故答案为:21.
2.5
【分析】本题考查了相似三角形的判定与性质,从实际问题中抽离出数学图形是解题的关键.证明,从而得到,代入数值即可求解.
【详解】解:∵,,
∴,
∴,
∵,,段长为2.5,
∴,
∴.
故答案为:5.
3.45
【分析】如图:都与水平线的垂直,M,N是垂足,则,即,然后根据相似三角形的对应边成比例求解即可.
【详解】解:如图,都与水平线的垂直,M,N是垂足,则,
∵,
∴,
∴,
∵,
∴,即,
∴当时,,
故要使这块石头滚动,至少要将杠杆的A端向下压.
故答案为:45.
4.
【分析】(1)直接利用等腰三角形的“三线合一”的性质和相似三角形的判定和性质进行求解即可;
(2)先求出CE的长,再利用勾股定理和锐角三角函数进行求解即可.
【详解】(1)如图,连接,过A点作于F,
∵米,米,
∴米,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴(米),
故答案为:.
(2)由(1)可知:
过点G作交于点N,
∵,
∴,
∴,
∴,
∴在中,,
,
∴,
∴,
故点G距离底面的高度为米,
故答案为:.
【题型6 实验问题】
1.(1)解:由题意可得:,
则,
故,
即,
解得:,
经检验,是上述分式方程的解,
∴的长为;
(2)∵,
∴(),
∵光在镜面反射中的入射角等于反射角,
∴,
又∵,
∴,
∴,
∴,
解得:(),
∴灯泡到地面的高度为.
2.4
【分析】本题考查了相似三角形的判定与性质,设蜡烛火焰的高度是xcm,由相似三角形的性质得 ,进行计算即可得,理解题意,将实际问题转化为数学问题,掌握相似三角形的判定与性质是解题的关键.
【详解】解:设蜡烛火焰的高度是x,
由相似三角形的性质得,,
,
解得,
故答案为:4.
3.解:由题意和图可知:,
∴,
∴,
∵,,
∴,
∴,
解得:,
答:灯泡到地面的高度为1.2m.
4.(1)①根据题意: , ,
∴四边形为平行四边形,
∴;
②如图所示,线段即为所求;
(2)①如图所示,点即为所求;
②过点作分别交、于点、
∵
∴
,,
解得:,
路灯距离地面的高度为米.
【题型7 古文问题】
1.A
【分析】本题考查相似三角形解实际应用题,读懂题意,熟练应用相似三角形的判定与性质是解决问题的关键.由题意可知,根据相似三角形性质得到,设,由分别是正方形的边的中点可知,则,解得,从而得到正方形城邑边长步.
【详解】解: ,,
,
正方形中,,过点,
,则,
,
,
分别是正方形的边的中点,设,
,
步,步,
,即,解得负舍去值,
正方形城邑边长步,
故选:A.
2.57.5
【分析】根据题意可知△ABD∽△AFC,根据相似三角形的性质可求AC,进一步求解即可得到井深.
【详解】解:依题意可得△ABD∽△AFC,
∴AB:AC=BD:FC,
即5:AC=0.4:5,
解得AC=62.5,
=BC=AC-AB=62.5-5=57.5尺.
故答案为:57.5.
3.D
【分析】根据题意可知,从而可以得到对应边的比相等,从而可以求解;
【详解】∵点E,G分别为CD,AD的中点,
∴,,
∴,
又题意可得,,
∴,
∴,
而EF=30步,GH=750步,
即,
∴,
解得:,
∴步;
4.解:由题意得:,,,
,
,
,
,
,
,
,
,
,
,
解得:,
,
解得:,
山峰的高度为米,它和标杆的水平距离是440米.
【题型8 裁剪问题】
1.D
【分析】根据相似三角形的性质求得甲的面积和丙的面积,进一步求得乙和丁的面积,比较即可求得.
【详解】解:如图:
∵AD⊥BC,AB=AC,
∴BD=CD=5+2=7,
∵AD=2+1=3,
∴S△ABD=S△ACD==
∵EF∥AD,
∴△EBF∽△ABD,
∴=()2=,
∴S甲=,
∴S乙=,
同理=()2=,
∴S丙=,
∴S丁=﹣=,
∵,
∴面积最大的是丁,
故选:D.
2.8
【分析】设,判断出和为等腰直角三角形,证明,得到,可求出,即可得到正方体礼品盒的棱长,从而计算体积.
【详解】解:如图,在正方形中,,
设,
由此裁剪可得:和为等腰直角三角形,
∴,
∴,即,
解得:,
∴,
∴正方体礼品盒的棱长为2,
∴体积为立方分米,
故答案为:8.
3.(1)如图1,延长FG交BC于H,
设CE=x,则E'H'=CE=x,
由轴对称的性质得:D'E'=DC=E'F'=9,
∴H'F'=AF=9+x,
∵AD=BC=16,
∴DF=16 (9+x)=7 x,
即C'D'=DF=7 x=F'G',
∴FG=7 x,
∴GH=9 (7 x)=2+x,EH=16 x (9+x)=7 2x,
∴EH∥AB,
∴△EGH∽△EAB,
∴,
∴,
解得x=1或31(舍),、及FG
∴AF=9+x=10,EC=1,故AF -EC=9
故答案为:9;
(2)由(1)得FG=7 x =7-1=6.
4.解:(1)∵AC⊥BD,
∴小风筝的面积S=AC BD=×12×14=84(cm)2;
(2)∵小风筝与大风筝形状完全相同,
∴假设大风筝的四个顶点为A′,B′,C′,D′,
∴△ABCD∽△A′B′C′D′,
∵它们的对应边之比为1:3,
∴A′C′=3AC=42cm,
同理B′D′=3BD=36cm,
∴至少需用42+36=78cm的材料;
(3)从四个角裁剪下来废弃不用的彩色纸的面积=矩形的面积﹣大风筝的面积=42×36﹣9×84=756(cm2).
【题型9 现实生活相关问题】
1.A
【分析】本题考查了相似三角形的判定与性质,勾股定理,轴对称的性质,连接,延长交于,由勾股定理得出,根据轴对称的性质得出,,证明,由相似三角形的性质计算即可得出答案.
【详解】解:如图,连接,延长交于,
,
在中,,
∵铁夹的剖面图是轴对称图形,
∴,,
∴
∵,
∴,
∴,即,
解得:,
∴,
故选:A.
2.C
【分析】本题主要考查了相似三角形的应用.利用相似三角形的判定与性质进而求出的长即可得出的长.
【详解】解:由题意可得:,则,
∴,
∵,
∴,
∴,
∵,,
∴,
即,解得:,
∵,
∴,即,解得:,
∴.
故选C.
3.
【分析】本题考查了相似三角形的应用.熟练掌握相似三角形的应用是解题的关键.
证明,则,即,计算求解即可.
【详解】解:∵,
∴,
∴,即,
解得,,
故答案为:.
【题型10 三角形内接矩形问题】
1.6
【分析】利用求得,然后求得,这样就可以计算得小长方形一共有4层,然后再次利用相似比,可求得每层可分割几个小长方形,最后确定小长方形的总数即可.
【详解】如图:当最上层的小长方形的一边与AB、AC交于点E、F时,
∴
∴,且,,
∴
∴
∵小长方形的宽为
∴能分割四层小长方形
设最底层的上一层的靠近点A的边为x
根据三角形相似可得:
解得,正好能分割两个小长方形
再上一层靠近点A的边就会小于,因此只能分割一个小长方形,且最上层分割了一个小长方形
∴按如图方式分割成的小长方形零件最多有个
故答案为6
2.
【分析】此题主要考查了相似三角形的应用,直接利用相似三角形的判定与性质得出,进而得出,的长,即可得出答案.
【详解】矩形中,,,
∴,
,
,
∵,
,
,
∵矩形零件的长与宽的比为,
设 ,,则,,
,
解得:,
,,
矩形的周长为: .
故答案为:.
3.解:如图,过点作于点,交于点.
,,
,
四边形是矩形,
,,
,
,
,
,
,
,
,
,
,
.
4.解:(1)①,理由如下:
∵米,米,米,米,
∴,
又∵,
∴,
②∵,
∴,
∴米.
(2)如图所示,作交于点G,
∵平方米,
∴平方米,
∴米,
∵四边形为矩形,
∴,
∴,
∴,
设,则,即,,
在中,由勾股定理得,
∴,
∵,
∴当时,最小,最小为,即最小为,
此时,,
∴,
∴最小值为,此时花卉种植区域的面积为平方米.
【题型1 建筑物高问题】
1.小亮运用《数书九章》中测量塔高的方法测量一幢楼房的高度.如图,表示楼房的高,表示一根直杆顶端到地面的高,表示小亮的眼睛到地面的高,在同一平面内,点在同一条直线上.已知,,,,小亮从点远眺楼顶,视线恰好经过直杆的顶端,请帮小亮求出楼房的高.
2.圭表是中国古代根据日影长度变化测定季节、划分四季和推算历法的工具.图1为圭表示意图.某同学受到启发,利用一根标杆和一个卷尺轻松测量出学校旗杆的高度.如图2,旗杆的影长在水平地面上,将标杆(长度1米)竖直放置在影长的最远端点A处,此时标杆的影长为.经测量,米,米.
(1)根据以上信息,计算旗杆的高度.(结果保留整数)
(2)若该同学在操作过程中,测量完的长度后,准备测量的长度时,发现卷尺不够长,又去寻找更长一点的卷尺,半小时后回来测量的长度,请问这样可以准确得到旗杆的高度吗?简单说明理由.
3.小明和小亮两位同学春节期间在游览某景区时,对景区内一座古塔产生浓厚的兴趣,他们想用所学的知识测量古塔的高度.为了保护古塔,工作人员在古塔底部设有栅栏,古塔底部不可直接到达.经询问得知栅栏长17米(即米),小亮在F处利用1米高的栅栏(即米,且),在栅栏顶端G处测得塔的顶部A处的仰角为,小明同学在古塔另一侧的C处放置平面镜(点D,C,B,F四点在一条直线上),当他站在D处时恰好能从平面镜中看到古塔的塔顶A,已知小明的身高为米(即米,且),小明到平面镜的水平距离为米(即米),求古塔的高.
4.图Ⅰ是大拇指广场示意图及测量其高度的方案,图Ⅱ是求大拇指高度的示意图.如图Ⅱ,在C处放置一根高度为2m且与地平线垂直的竹竿,点A,I,D在同一直线上,测得为.将竹竿3m平移至E处,点A,G,F在同一直线上,测得为.求大拇指的高度.
【题型2 影长问题】
1.如图1,平直的公路旁有一灯杆,在灯光下,小丽从灯杆的底部处沿直线前进到达点,在处测得自己的影长.小丽身高.
(1)求灯杆的长;
(2)若小丽从D处继续沿直线前进到达G处(如图2),求此时小丽的影长的长.
2.操场上有一根竖直的旗杆,它的一部分影子()落在水平地面上,另一部分影子()落在对面的墙壁上,经测量,墙壁上的影高为,地面的影长为,同时测得一根高为的竹竿的影长是,请根据以上信息,则旗杆的高度是( )
A. B. C. D.
3.如图,在路灯下,表示小明的身高,表示他的影子,表示小亮的身高,路灯灯泡在线段上.
(1)请你画出灯泡的位置,并画出小亮在灯光下的影子;
(2)如果小明的身高,他的影子,且他到路灯的距离,求路灯的高.
4.小明和爸爸在公园散步,此时爸爸的影子落在了身后的地面和墙上,如图1所示.其中,段为地上的影子,段为墙上的影子.小明想利用所学知识测量出爸爸的身高.他向工作人员询问得知:公园地面与墙面所用均为厚度,长度的砖块,小明数了一下,段刚好是4块地砖的长度,而段恰好为4块地砖的厚度;同一时刻,小明观察到公园门口指示牌影子的顶端刚好到达保安亭,如图2所示,其中为指示牌的影子.已知爸爸、墙面、指示牌和保安亭均与地面垂直,指示牌高,指示牌距保安亭,请你根据以上信息,帮小明求出爸爸的身高.
【题型3 河宽问题】
1.学完《相似》一章后,某中学数学实践小组决定利用所学知识去测量河的宽度.如图,这条河的两岸是平行的,小丽站在离南岸20米(即米)的点处懒北岸,小军、小强站在南岸边,调整小军、小强两人的位置,当小军、小强两人分别站在两点处时,小丽发现河北岸边的两根电线杆恰好被小军、小强遮挡(即三点共线,三点共线).已知电线杆之间的距离为75米,小军、小强两人之间的距离为30米,求这条河的宽度.
2.周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
3.如图,为了测量某河段的宽度,某校数学课外活动小组在河对岸选定一个目标点A,在近岸取点B和C,使点A、B、C共线且直线AB与河岸b垂直,接着在过点C且与AB垂直的直线a上选择适当的点D,点A、D与河岸b上的点E在一条直线上.测得,,,请根据这些数据,计算河宽AB.
4.如图,为了测量平静的河面的宽度,即的长,在离河岸点米远的点,立一根长为米的标杆,在河对岸的岸边有一根长为米的电线杆,电线杆的顶端在河里的倒影为点,即,两岸均高出水平面米,即米,经测量此时、、三点在同一直线上,并且点、、、共线,点、、共线,若、、均垂直于河面,求河宽是多少米?
【题型4 树高问题】
1.《周髀算经》中记载了“平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).小南利用“矩”可测量大树的高度.如图,通过不断调整自己的姿势和“矩”的摆放位置,使斜边保持水平,并且边与点B在同一直线上,已知“矩”的两边长分别为,,小南的眼睛到地面的距离为,测得,求树高.
2.如图,直立在B处的标杆AB=2.9米,小爱站在F处,眼睛E处看到标杆顶A,树顶C在同一条直线上(人,标杆和树在同一平面内,且点F,B,D在同一条直线上).已知BD=6米,FB=2米,EF=1.7米,求树高CD.
3.小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器CD,测得;再在BD的延长线上确定一点G,使米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得米,小明眼睛与地面的距离米,测量器的高度米.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(小平面镜的大小忽略不计)
4.小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他利用镜子进行两次测量,如图,第一次他把镜子放在点处,他在点处正好在镜中看到树尖的像;第二次他把镜子放在点处,他在点处正好在镜中看到树尖的像.已知,,,小军的眼睛距地面(即),量得,求这棵古松树的高度.(镜子大小忽略不计)
【题型5 杠杆问题】
1.阿基米德曾说过:“给我一个支点和一根足够长的杆子,我就能撬起整个地球.”这句话的意思是利用物理学中的杠杆原理,只要有合适的支点和合适的工具,就可以把地球轻松搬动.如图1,这是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图2中,杠杆的D端被向上翘起的距离,动力臂与阻力臂满足(与相交于点O),则的长为 cm.
2.如图,是一个杠杆,可绕支点自由转动,当处于图中的位置时,点到点的水平距离,点到点的水平距离,若已知杠杆的段长为2.5,则杠杆的段长为 .
3.如图是用杠杆撬石头的示意图,点C是支点,当用力压杠杆的A端时,杠杆绕C点转动,另一端B向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B端必须向上翘起,已知,要使这块石头滚动,至少要将杠杆的A端向下压 .
4.如图所示的是古代一种可以远程攻击的投石车,图是投石车投石过程中某时刻的示意图,是杠杆,弹袋挂在点,重锤挂在点,点A为支点,点是水平底板上的一点,米,米.
(1)投石车准备时,点恰好与点重合,此时和垂直,则 米
(2)投石车投石过程中,的延长线交线段于点,若::,则点距地面为 米.
【题型6 实验问题】
1.如图,嘉嘉同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)求的长.
(2)求灯泡到地面的高度.
2.约在两千五百年前,如图(1),墨子和他的学生做了世界上第1个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图(2)所示的小孔成像实验中,若物距为,像距为,蜡烛火焰倒立的像的高度是,则蜡烛火焰的高度是 .
3.如图,佳佳同学正在使用手电筒进行物理光学实验,水平地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处,点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,木板到平面镜的水平距离,已知光在镜面反射中的入射角等于反射角,求灯泡到地面的高度.
4.小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将木杆水平放置,此时木杆在水平地面上的影子为线段.
①若木杆的长为,则其影子的长为___________;
②在同一时刻同一地点,将另一根木杆直立于地面,请画出表示此时木杆在地面上影子的线段:
(2)如图2,夜晚在路灯下,小桃将木杆水平放置,此时木杆在水平地面上的影子为线段.
①请在图中画出表示路灯灯泡位置的点;
②若木杆的长为,经测量木杆距离地面,其影子的长为,则路灯距离地面的高度为___________.
【题型7 古文问题】
1.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何?”它的意思是:如图,M,N分别是正方形的边,的中点,,,过点A,且步,步,那么该正方形城邑边长约为( )步.
A.300 B.250 C.225 D.150
2.《九章算术》是我国古代数学名著,书中有如下问题: “今有井径尺,不知其深,立五尺木于井上,从木末 望水岸,入径四寸.问井深几何?”意思是:如图, 井径尺,立木高尺,寸尺,则井深为 尺.
3.《九章算术》是我国数学经典,上面记载:“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方几何?”其意思是:如图,已知正方形小城ABCD,点E,G分别为CD,AD的中点,EF⊥CD,GH⊥AD,点F,D,H在一条直线上,EF=30步,GH=750步.正方形小城ABCD的边长是( )
A.150步 B.200步 C.250步 D.300步
4.“度高者重表,测深者累矩,孤离者三望,离而又旁求者四望.触类而长之,则虽幽遐诡伏,靡所不入.”就是说,使用多次测量传递的方法,就可以测量出各点之间的距离和高度差.——刘徽《九章算术注·序》.某市科研考察队为了求出某海岛上的山峰的高度,如图,在同一海平面的处和处分别树立标杆和,标杆的高都是5.5米,两处相隔80米,从标杆向后退11米的处,可以看到顶峰和标杆顶端在一条直线上;从标杆向后退13米的处,可以看到顶峰和标杆顶端在一条直线上.求山峰的高度及它和标杆的水平距离.
注:图中各点都在一个平面内.
【题型8 裁剪问题】
1.有一等腰三角形纸片ABC,AB=AC,裁剪方式及相关数据如图所示,则得到的甲、乙、丙、丁四张纸片中,面积最大的是( )
A.甲 B.乙 C.丙 D.丁
2.三八妇女节,同学们准备送小礼物给妈妈,首先利用正方形纸板,制作一个正方体礼品盒(如图所示裁剪).已知正方形纸板边长为分米,则这个礼品盒的体积 立方分米.
3.在综合实践课中,小慧将一张长方形卡纸如图1所示裁剪开,无缝隙不重叠的拼成如图2所示的“”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知,,.
求(1)线段与的差值是___
(2)的长度.
4.一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分别为12cm和14cm.
(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
【题型9 现实生活相关问题】
1.如图是一个常见的铁夹的剖面图,,表示铁夹的剖面的两条边,点是转动轴的位置,,垂足为,,,,且铁夹的剖面图是轴对称图形,则,两点间的距离为( )
A. B. C. D.
2.如图,已知箱子沿着斜面向上运动,箱高.当时,点B到地面的距离,则点A到地面的距离为( )
A. B. C. D.
3.如图①,是生活中常见的人字梯,也称折梯,因其使用时,左右的梯杆及地面构成一个等腰三角形,因而把它形象的称为“人字梯”.如图②,是其工作示意图,拉杆米,则两梯杆跨度B、C之间距离为 米.
【题型10 三角形内接矩形问题】
1.有一块锐角三角形余料,边为,边上的高为,现要把它分割成若干个邻边长分别为和的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为的边在上,则按如图方式分割成的小长方形零件最多有 .
2.如图,有一块三角形余料ABC,它的边,高,现在要把它加工成长与宽的比为的矩形零件,要求一条长边在上,其余两个顶点分别在,上,则矩形的周长为 cm.
3.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图,是他研究的一个汽车盲区的示意图,为驾驶员的盲区,驾驶员的眼睛点处与地面的距离为,车宽,车头近似看成一个矩形,且满足,求汽车盲区的长度.
4.(1)【问题探究】如图①,点B,C分别在上,米,米,米,米,米.
①探究与是否相似并说明理由;
②求的长.
(2)【问题解决】如图②,四边形规划为园林绿化区,对角线将整个四边形分成面积相等的两部分,已知米,四边形的面积为平方米,为了更好地美化环境,政府计划在边上分别确定点E,F,在边上确定点P,Q,使四边形为矩形,在矩形内种植花卉,在四边形剩余区域种植草坪,为了方便市民观赏,计划在之间修一条小路,并使得最短,根据设计要求,求出的最小值,并求出当最小时,花卉种植区域的面积.
参考答案
【题型1 建筑物高问题】
1.解:过作于,交于E,
则,,,
,,
,
,
,
,
,
,
答:楼房的高为.
2.(1)解:由题意,可知.
∴.
又∵,
∴.
∴,即.
∴(米).
答:旗杆MN的高度约为10米.
(2)解:不可以.
理由如下:旗杆和标杆的影长随着时间变化而变化,必须同时测量,小明测量标杆影长后半个小时再测旗杆影长,此时旗杆影长已发生变化,故不可以准确得到旗杆的高度.(理由合理即可)
3.解:如图:过点G作,垂足为H,
由题意得:米,
设米,
∵米,
∴米,
在中,,
∴米,
∴米,
由题意得:,
∴,
∴,
∴,即:,解得:,
∴,解得:,
∴(米),
∴古塔的高为12米.
4.解:由题意可得:,
∴.
∴.
由题意可得:,
∴.
∴.
∵,
∴,即,解得:.
将代入,得.解得.
∴大拇指的高度为.
【题型2 影长问题】
1.(1)解:如图1,根据题意得:,(米,
,
,
即,
解得:(米;
答:灯杆的高度为;
(2)如图2,根据题意得:,(米,
,
,
即,
解得:(米;
答:此时小丽的影长的长是.
2.C
【分析】过点D作于点E,根据题意,,得到矩形,继而得到,根据同一时刻,物高与影长成正比,建立等式计算即可.
本题考查了矩形的判定和性质,相似三角形的应用,熟练掌握解矩形的应用是解题的关键.
【详解】过点D作于点E,根据题意,得,
∴四边形为矩形,
∴,
∵,,
∴,
根据同一时刻,物高与影长成正比,
∴即,
解得,
∴.
故选C.
3.(1)解:如图,
点O为灯泡的位置, FH为小亮在灯光下的影子;
(2)解:,
,
,
,
解得:,
路灯的高为.
4.解:如图:过点作,垂足为,
由题意得:,,
指示牌高,指示牌距保安亭,
,
,
,
爸爸的身高为.
【题型3 河宽问题】
1.解:延长交于点,如解图所示.
依题意,米,米.
设这条河的宽度为米.
,
.
,
即,
解得.
答:这条河的宽度为30米.
2.解:∵CB⊥AD,ED⊥AD,
∴∠CBA=∠EDA=90°,
∵∠CAB=∠EAD,
∴ ABC∽ ADE,
∴,
又∵AD=AB+BD,BD=8.5,BC=1,DE=1.5,
∴,
∴AB=17,
即河宽为17m.
3.解:由题意得,,
∴,
∴,即.
∵,,,
∴ ,
解得 .
答:河宽AB大约是20m.
4.解:延长交的反向延长线于点,
则四边形是矩形,
,,
,
,
,
,
,
,
,米,米,
米,
,,
,
,
,
,
,
,
答:河宽是12米.
【题型4 树高问题】
1.解:据题意可得,,
,
.
,,,
,
,
.
答:树高为.
2.解:过E作EH⊥CD交CD于H点,交AB于点G,则EH⊥AB,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB,
∴四边形EFDH为矩形,
∴EF=GB=DH=1.7米,EG=FB=2米,GH=BD=6米,
∴AG=AB GB=2.9 1.7=1.2(米),
∵AG∥CH,
∴△AEG∽△CEH,
∴,
∴,
∴CH=4.8,
∴CD=CH+DH=4.8+1.7=6.5(米).
答:树高CD为6.5米.
3.如图,过点作于点,则,,
在 中,,
∴,
∴,
∵,,
∴
由反射角等于入射角得,
∴,
∴,即,
解得
∴
∴这棵树高18米.
4.解:∵,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,,,
∴,
解得:,
∴,
解得:,
答:这棵古松树的高度为m.
【题型5 杠杆问题】
1.解:由题意得,,
,
,
,
,
cm.
故答案为:21.
2.5
【分析】本题考查了相似三角形的判定与性质,从实际问题中抽离出数学图形是解题的关键.证明,从而得到,代入数值即可求解.
【详解】解:∵,,
∴,
∴,
∵,,段长为2.5,
∴,
∴.
故答案为:5.
3.45
【分析】如图:都与水平线的垂直,M,N是垂足,则,即,然后根据相似三角形的对应边成比例求解即可.
【详解】解:如图,都与水平线的垂直,M,N是垂足,则,
∵,
∴,
∴,
∵,
∴,即,
∴当时,,
故要使这块石头滚动,至少要将杠杆的A端向下压.
故答案为:45.
4.
【分析】(1)直接利用等腰三角形的“三线合一”的性质和相似三角形的判定和性质进行求解即可;
(2)先求出CE的长,再利用勾股定理和锐角三角函数进行求解即可.
【详解】(1)如图,连接,过A点作于F,
∵米,米,
∴米,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
∴(米),
故答案为:.
(2)由(1)可知:
过点G作交于点N,
∵,
∴,
∴,
∴,
∴在中,,
,
∴,
∴,
故点G距离底面的高度为米,
故答案为:.
【题型6 实验问题】
1.(1)解:由题意可得:,
则,
故,
即,
解得:,
经检验,是上述分式方程的解,
∴的长为;
(2)∵,
∴(),
∵光在镜面反射中的入射角等于反射角,
∴,
又∵,
∴,
∴,
∴,
解得:(),
∴灯泡到地面的高度为.
2.4
【分析】本题考查了相似三角形的判定与性质,设蜡烛火焰的高度是xcm,由相似三角形的性质得 ,进行计算即可得,理解题意,将实际问题转化为数学问题,掌握相似三角形的判定与性质是解题的关键.
【详解】解:设蜡烛火焰的高度是x,
由相似三角形的性质得,,
,
解得,
故答案为:4.
3.解:由题意和图可知:,
∴,
∴,
∵,,
∴,
∴,
解得:,
答:灯泡到地面的高度为1.2m.
4.(1)①根据题意: , ,
∴四边形为平行四边形,
∴;
②如图所示,线段即为所求;
(2)①如图所示,点即为所求;
②过点作分别交、于点、
∵
∴
,,
解得:,
路灯距离地面的高度为米.
【题型7 古文问题】
1.A
【分析】本题考查相似三角形解实际应用题,读懂题意,熟练应用相似三角形的判定与性质是解决问题的关键.由题意可知,根据相似三角形性质得到,设,由分别是正方形的边的中点可知,则,解得,从而得到正方形城邑边长步.
【详解】解: ,,
,
正方形中,,过点,
,则,
,
,
分别是正方形的边的中点,设,
,
步,步,
,即,解得负舍去值,
正方形城邑边长步,
故选:A.
2.57.5
【分析】根据题意可知△ABD∽△AFC,根据相似三角形的性质可求AC,进一步求解即可得到井深.
【详解】解:依题意可得△ABD∽△AFC,
∴AB:AC=BD:FC,
即5:AC=0.4:5,
解得AC=62.5,
=BC=AC-AB=62.5-5=57.5尺.
故答案为:57.5.
3.D
【分析】根据题意可知,从而可以得到对应边的比相等,从而可以求解;
【详解】∵点E,G分别为CD,AD的中点,
∴,,
∴,
又题意可得,,
∴,
∴,
而EF=30步,GH=750步,
即,
∴,
解得:,
∴步;
4.解:由题意得:,,,
,
,
,
,
,
,
,
,
,
,
解得:,
,
解得:,
山峰的高度为米,它和标杆的水平距离是440米.
【题型8 裁剪问题】
1.D
【分析】根据相似三角形的性质求得甲的面积和丙的面积,进一步求得乙和丁的面积,比较即可求得.
【详解】解:如图:
∵AD⊥BC,AB=AC,
∴BD=CD=5+2=7,
∵AD=2+1=3,
∴S△ABD=S△ACD==
∵EF∥AD,
∴△EBF∽△ABD,
∴=()2=,
∴S甲=,
∴S乙=,
同理=()2=,
∴S丙=,
∴S丁=﹣=,
∵,
∴面积最大的是丁,
故选:D.
2.8
【分析】设,判断出和为等腰直角三角形,证明,得到,可求出,即可得到正方体礼品盒的棱长,从而计算体积.
【详解】解:如图,在正方形中,,
设,
由此裁剪可得:和为等腰直角三角形,
∴,
∴,即,
解得:,
∴,
∴正方体礼品盒的棱长为2,
∴体积为立方分米,
故答案为:8.
3.(1)如图1,延长FG交BC于H,
设CE=x,则E'H'=CE=x,
由轴对称的性质得:D'E'=DC=E'F'=9,
∴H'F'=AF=9+x,
∵AD=BC=16,
∴DF=16 (9+x)=7 x,
即C'D'=DF=7 x=F'G',
∴FG=7 x,
∴GH=9 (7 x)=2+x,EH=16 x (9+x)=7 2x,
∴EH∥AB,
∴△EGH∽△EAB,
∴,
∴,
解得x=1或31(舍),、及FG
∴AF=9+x=10,EC=1,故AF -EC=9
故答案为:9;
(2)由(1)得FG=7 x =7-1=6.
4.解:(1)∵AC⊥BD,
∴小风筝的面积S=AC BD=×12×14=84(cm)2;
(2)∵小风筝与大风筝形状完全相同,
∴假设大风筝的四个顶点为A′,B′,C′,D′,
∴△ABCD∽△A′B′C′D′,
∵它们的对应边之比为1:3,
∴A′C′=3AC=42cm,
同理B′D′=3BD=36cm,
∴至少需用42+36=78cm的材料;
(3)从四个角裁剪下来废弃不用的彩色纸的面积=矩形的面积﹣大风筝的面积=42×36﹣9×84=756(cm2).
【题型9 现实生活相关问题】
1.A
【分析】本题考查了相似三角形的判定与性质,勾股定理,轴对称的性质,连接,延长交于,由勾股定理得出,根据轴对称的性质得出,,证明,由相似三角形的性质计算即可得出答案.
【详解】解:如图,连接,延长交于,
,
在中,,
∵铁夹的剖面图是轴对称图形,
∴,,
∴
∵,
∴,
∴,即,
解得:,
∴,
故选:A.
2.C
【分析】本题主要考查了相似三角形的应用.利用相似三角形的判定与性质进而求出的长即可得出的长.
【详解】解:由题意可得:,则,
∴,
∵,
∴,
∴,
∵,,
∴,
即,解得:,
∵,
∴,即,解得:,
∴.
故选C.
3.
【分析】本题考查了相似三角形的应用.熟练掌握相似三角形的应用是解题的关键.
证明,则,即,计算求解即可.
【详解】解:∵,
∴,
∴,即,
解得,,
故答案为:.
【题型10 三角形内接矩形问题】
1.6
【分析】利用求得,然后求得,这样就可以计算得小长方形一共有4层,然后再次利用相似比,可求得每层可分割几个小长方形,最后确定小长方形的总数即可.
【详解】如图:当最上层的小长方形的一边与AB、AC交于点E、F时,
∴
∴,且,,
∴
∴
∵小长方形的宽为
∴能分割四层小长方形
设最底层的上一层的靠近点A的边为x
根据三角形相似可得:
解得,正好能分割两个小长方形
再上一层靠近点A的边就会小于,因此只能分割一个小长方形,且最上层分割了一个小长方形
∴按如图方式分割成的小长方形零件最多有个
故答案为6
2.
【分析】此题主要考查了相似三角形的应用,直接利用相似三角形的判定与性质得出,进而得出,的长,即可得出答案.
【详解】矩形中,,,
∴,
,
,
∵,
,
,
∵矩形零件的长与宽的比为,
设 ,,则,,
,
解得:,
,,
矩形的周长为: .
故答案为:.
3.解:如图,过点作于点,交于点.
,,
,
四边形是矩形,
,,
,
,
,
,
,
,
,
,
,
.
4.解:(1)①,理由如下:
∵米,米,米,米,
∴,
又∵,
∴,
②∵,
∴,
∴米.
(2)如图所示,作交于点G,
∵平方米,
∴平方米,
∴米,
∵四边形为矩形,
∴,
∴,
∴,
设,则,即,,
在中,由勾股定理得,
∴,
∵,
∴当时,最小,最小为,即最小为,
此时,,
∴,
∴最小值为,此时花卉种植区域的面积为平方米.
