北京市京源学校2024-2025学年八年级下数学期中考试试卷(PDF版,无答案)
文档属性
| 名称 | 北京市京源学校2024-2025学年八年级下数学期中考试试卷(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 627.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-03 10:53:46 | ||
图片预览



文档简介
北京市京源学校 2024-2025 学年度第二学期期中考试
初二年级 数学试卷
一、 选择题(本题共 16分,每小题 2分)
1.中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是
A.京剧脸谱 B.剪纸对鱼 C.中国结 D.风筝燕归来
2.在平面直角坐标系 xOy 中,点P(1, 2 ) 关于原点对称的点的坐标是
A. ( 1,2 ) B. (1, 2 ) C. ( 2,1 ) D. (2, 1)
3.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是
A.三角形 B.四边形 C.五边形 D.六边形
4.下列图象中,y 不是 x 的函数的是
y y y y
O x O x O x O x
A. B. C. D.
5.在平面直角坐标系 xOy 中,过点 P(-2,3)作 PA⊥y 轴,垂足为点 A,则 PA 的长为
A.3 B.2 C.5 D. 13
6.顺次连接矩形各边中点所围成的四边形是
A.平行四边形 B.矩形 C.菱形 D.正方形
7.菱形 ABCD 的边长为 5,一条对角线长为 6,则菱形面积为
A.20 B.24 C.30 D.48
第1页(共 8 页)
2a b, (a b)
8.若定义一种新运算:a b =
2a +b 12,(a b)
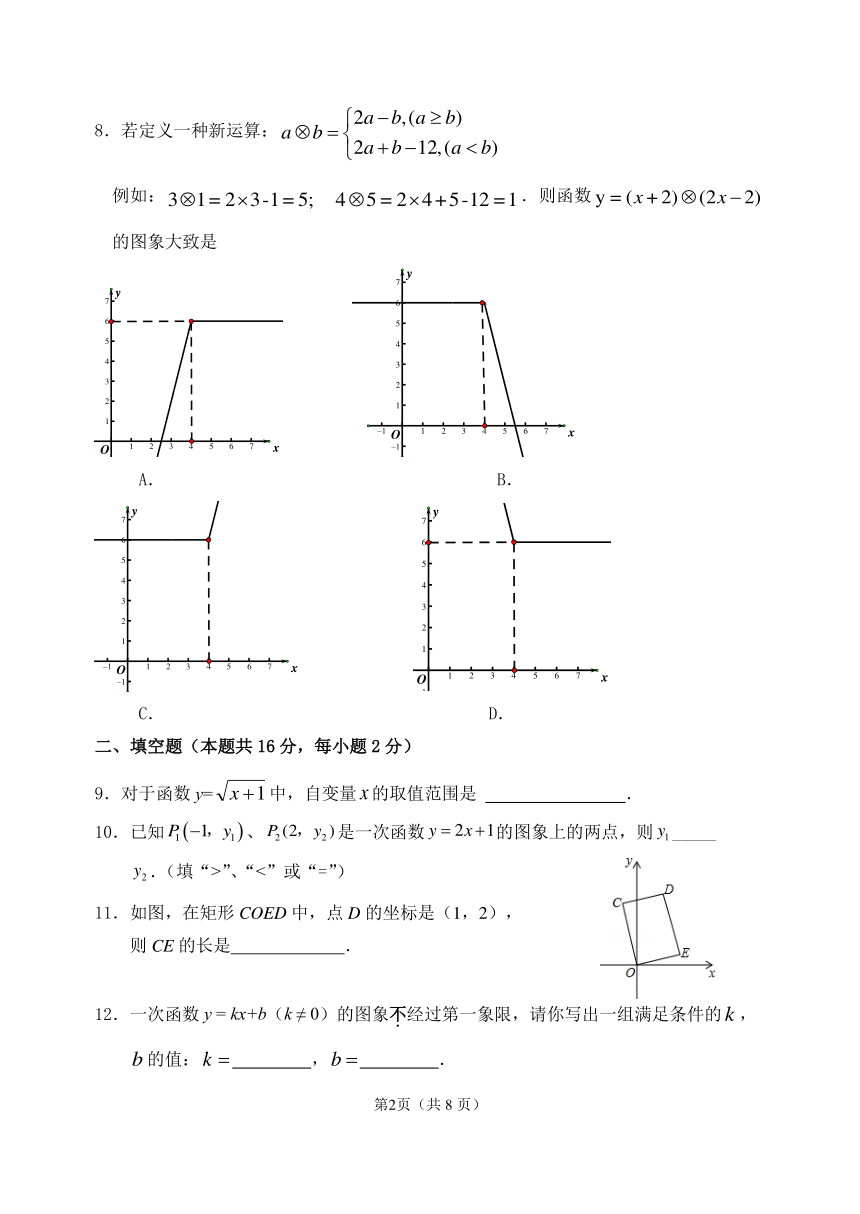
例如:3 1= 2 3-1= 5; 4 5 = 2 4 +5-12 =1.则函数 y = (x + 2) (2x 2)
的图象大致是
y
7
y
7 6
6 5
5 4
4 3
3 2
2
1
1
–1 O 1 2 3 4 5 6 7 x
–1 O 1 2 3 4 5 6 7 x –1
–1
A. B.
y y
7 7
6 6
5 5
4
4
3
3
2
2
1
1
–1 O 1 2 3 4 5 6 7 x
–1 1 2 3 4 5 6 7
–1 x O–1
C. D.
二、填空题(本题共 16 分,每小题 2分)
9.对于函数 y= x +1中,自变量 x的取值范围是 .
10.已知P ( 1,y )、 P (2,y )是一次函数 y = 2x +11 1 2 2 的图象上的两点,则 y1 _____
y2 .(填“>”、“<”或“=”)
11.如图,在矩形 COED 中,点 D 的坐标是(1,2),
则 CE 的长是 .
12.一次函数 y = kx+b(k ≠ 0)的图象不.经过第一象限,请你写出一组满足条件的k ,
b 的值: k = ,b = .
第2页(共 8 页)
13.如图,在正方形 中,点 在对角线 上,且∠ = 60°,延长 交 于点
,连接 ,则∠ 的度数为 .
14.如图,一次函数 y = kx +b 的图象经过点 A(1,2),关于 x 的不等式kx+b 2的解
集为 .
第 14 题图
第 13题图 第 16题图
15.若直线 y = kx + 2与两条坐标轴围成的三角形的面积是 2,则 k的值为 .
16.如图,在正方形 ABCD中,对角线 AC 与 BD相交于点O, E 为BC上一点,
CE =5, F 为DE 的中点.若 CEF 的周长为 18,则OF 的长为______ __.
三、解答题(本题共 68分,第 17~22题每小题 5分,第 23~26题每小题 6分,第
27~28题每小题 7分)解答应写出文字说明、证明过程或演算步骤.
17.已知一次函数 y = kx + b( k 0)的图象经过点 A( 2 , 5) ,B(0 ,1),求一次函数的
表达式.
18.如图,在平行四边形 ABCD 中,E,F 分别是 BC,AD 上的点,且 AE∥CF.
求证:BE=DF.
A F D
B E C
19.下面是小王设计的“利用直角和线段作矩形”的尺规作图过程.
已知:如图 1,线段 a,b,及∠MAN=90°. M
求作:矩形 ABCD,使 AB=a,AD=b.
a
b
A N
图 1
第3页(共 8 页)
作法:如图 2,
①在射线 AM,AN 上分别截取 AB=a,AD=b; M
②以 B 为圆心,b 长为半径作弧,再以 D 为圆心,
a 长为半径作弧,两弧在∠MAN 内部交于点 C; B
③连接 BC,DC. a
∴ 四边形 ABCD 就是所求作的矩形.
A b D N
图 2
根据小王设计的尺规作图过程,解答下列问题:
(1)使用直尺和圆规,依作法补全图 2(保留作图痕迹);
(2)完成下面的证明.
证明:
∵ AB= DC=a,AD= =b,
∴ 四边形 ABCD 是平行四边形( ) (填推理的依据).
∵ ∠MAN=90°,
∴ 四边形 ABCD 是矩形( )(填推理的依据).
20.某种机器工作前先将空油箱加满(加.油.过.程.).,然后停止加油立即开始工作(加.工.过.
程.),当停止工作时,油箱中油量为 10 升.在整个过程中,油箱里的油量 y(单位:
升)与时间 x(单位:分)之间的关系如图所示.
(1)机器加.油.过.程.中每分钟加油量为 升,机器加.工.过.程.中每分钟耗油量
为 升.
(2)求机器加.工.过.程.时 y 关于 x 的函数解析式;
(3)当油箱中油量为油箱容积的一半时,直接写出 x 的值.
y (升)
90
10
O 10 90 x (分)
第4页(共 8 页)
21.如图,在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,延长 CB 到点 E,使BE = BC,
连接 AE .
(1)求证:四边形 AEBD 是平行四边形;
(2)若 CD=13,AC=10,求 AE 的值.
A D
O
E
B C
22.在平面直角坐标系 xOy 中,一次函数 y kx+b(k≠0)的图象,由函数 y=x 的图
象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当 x >1 时,对于 x 的每一个值,函数 y m(x m 0)的值大于一次函数
y kx+b 的值,直接写出 m 的取值范围.
y
4
3
2
1
–4 –3 –2 –1 O 1 2 3 4 x
–1
–2
–3
23.一次函数 y = kx+1(k ≠ 0)的图象过点 P(-3,2),与 x 轴交于点 A,与 y 轴交于点
B.
(1)求 k 的值及点 A、B 的坐标;
(2)已知点 C(-1,0),若以 A,B,C,D 为顶点的四边形是平行四边形,请直接写
出所有符合条件的点 D 的坐标.
第5页(共 8 页)
24.如图,在菱形 ABCD 中,∠B=60°,AB=1,延长 AD到点 E,使 DE=AD,延长 CD 到
点 F,使 DF=CD,连接 AC、CE、EF、AF.
(1)求证:四边形 ACEF 是矩形;
(2)求四边形 ACEF 的周长.
A F
D
B
C E
25.如图,在平面直角坐标系 xOy 中,直线 l1经过原点,且与直线 l2:y=-x+3 交于
点 A(m,2),直线 l2与 x 轴交于点 B.
(1)求直线 l1 的函数解析式;
(2)点 P(n,0)在 x 轴上,过点 P 作平行于 y 轴的直线,分别交直线 l1与直线 l2 于点
M、N,若 MN=OB,求 n 的值.
26.如图,将矩形纸片 ABCD 沿过点 A 的直线翻折,点 B 恰好与其对角线 AC 的中点 O
重合,折痕与边 BC 交于点 E. 延长 EO 交 AD 于点 F,连接 CF.
(1)按要求补全图形;
(2)求证:四边形 AECF 是菱形;
A D
(3)若 AB= 6 ,求 BE 的长.
O
B E C
第6页(共 8 页)
27.如图,在正方形 ABCD 中,点 E 是边 AB 上的一动点(不与点 A、点 B 重合),连接
DE,点 A 关于直线 DE 的对称点为 F,连接 EF 并延长交 BC 边于点 G,连接 DF,
DG.
(1)依题意补全图形,并证明∠FDG=∠CDG;
(2)过点 E 作 EM⊥DE 于点 E,交 DG 的延长线于点 M,连接 BM.用等式表示
线段 AE,BM 的数量关系,并证明.
A D
E
F
B C
28.对于两个实数 a,b,规定 Max(a,b)表示 a,b 两数中较大者,特殊地,当 a = b
时,Max(a,b)=a.如:Max(1,2)= 2,Max(-1,-2)= -1,Max(0,0)=
0.
(1)Max(-1,0)= ,Max(n,n -2)= ;
(2)对于一次函数 y1 = x 2, y2 = x +b,
①当 x≥-1 时,Max(y1,y2)= y2,求 b 的取值范围;
②当 x=1-b 时,Max(y1,y2)=p,当 x=1+b 时,Max(y1,y2)=q,若
p≤q,直接写出 b 的取值范围.
第7页(共 8 页)
以下为草稿纸
第8页(共 8 页)
初二年级 数学试卷
一、 选择题(本题共 16分,每小题 2分)
1.中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是
A.京剧脸谱 B.剪纸对鱼 C.中国结 D.风筝燕归来
2.在平面直角坐标系 xOy 中,点P(1, 2 ) 关于原点对称的点的坐标是
A. ( 1,2 ) B. (1, 2 ) C. ( 2,1 ) D. (2, 1)
3.如果一个多边形的内角和等于一个三角形的外角和的两倍,那么这个多边形是
A.三角形 B.四边形 C.五边形 D.六边形
4.下列图象中,y 不是 x 的函数的是
y y y y
O x O x O x O x
A. B. C. D.
5.在平面直角坐标系 xOy 中,过点 P(-2,3)作 PA⊥y 轴,垂足为点 A,则 PA 的长为
A.3 B.2 C.5 D. 13
6.顺次连接矩形各边中点所围成的四边形是
A.平行四边形 B.矩形 C.菱形 D.正方形
7.菱形 ABCD 的边长为 5,一条对角线长为 6,则菱形面积为
A.20 B.24 C.30 D.48
第1页(共 8 页)
2a b, (a b)
8.若定义一种新运算:a b =
2a +b 12,(a b)
例如:3 1= 2 3-1= 5; 4 5 = 2 4 +5-12 =1.则函数 y = (x + 2) (2x 2)
的图象大致是
y
7
y
7 6
6 5
5 4
4 3
3 2
2
1
1
–1 O 1 2 3 4 5 6 7 x
–1 O 1 2 3 4 5 6 7 x –1
–1
A. B.
y y
7 7
6 6
5 5
4
4
3
3
2
2
1
1
–1 O 1 2 3 4 5 6 7 x
–1 1 2 3 4 5 6 7
–1 x O–1
C. D.
二、填空题(本题共 16 分,每小题 2分)
9.对于函数 y= x +1中,自变量 x的取值范围是 .
10.已知P ( 1,y )、 P (2,y )是一次函数 y = 2x +11 1 2 2 的图象上的两点,则 y1 _____
y2 .(填“>”、“<”或“=”)
11.如图,在矩形 COED 中,点 D 的坐标是(1,2),
则 CE 的长是 .
12.一次函数 y = kx+b(k ≠ 0)的图象不.经过第一象限,请你写出一组满足条件的k ,
b 的值: k = ,b = .
第2页(共 8 页)
13.如图,在正方形 中,点 在对角线 上,且∠ = 60°,延长 交 于点
,连接 ,则∠ 的度数为 .
14.如图,一次函数 y = kx +b 的图象经过点 A(1,2),关于 x 的不等式kx+b 2的解
集为 .
第 14 题图
第 13题图 第 16题图
15.若直线 y = kx + 2与两条坐标轴围成的三角形的面积是 2,则 k的值为 .
16.如图,在正方形 ABCD中,对角线 AC 与 BD相交于点O, E 为BC上一点,
CE =5, F 为DE 的中点.若 CEF 的周长为 18,则OF 的长为______ __.
三、解答题(本题共 68分,第 17~22题每小题 5分,第 23~26题每小题 6分,第
27~28题每小题 7分)解答应写出文字说明、证明过程或演算步骤.
17.已知一次函数 y = kx + b( k 0)的图象经过点 A( 2 , 5) ,B(0 ,1),求一次函数的
表达式.
18.如图,在平行四边形 ABCD 中,E,F 分别是 BC,AD 上的点,且 AE∥CF.
求证:BE=DF.
A F D
B E C
19.下面是小王设计的“利用直角和线段作矩形”的尺规作图过程.
已知:如图 1,线段 a,b,及∠MAN=90°. M
求作:矩形 ABCD,使 AB=a,AD=b.
a
b
A N
图 1
第3页(共 8 页)
作法:如图 2,
①在射线 AM,AN 上分别截取 AB=a,AD=b; M
②以 B 为圆心,b 长为半径作弧,再以 D 为圆心,
a 长为半径作弧,两弧在∠MAN 内部交于点 C; B
③连接 BC,DC. a
∴ 四边形 ABCD 就是所求作的矩形.
A b D N
图 2
根据小王设计的尺规作图过程,解答下列问题:
(1)使用直尺和圆规,依作法补全图 2(保留作图痕迹);
(2)完成下面的证明.
证明:
∵ AB= DC=a,AD= =b,
∴ 四边形 ABCD 是平行四边形( ) (填推理的依据).
∵ ∠MAN=90°,
∴ 四边形 ABCD 是矩形( )(填推理的依据).
20.某种机器工作前先将空油箱加满(加.油.过.程.).,然后停止加油立即开始工作(加.工.过.
程.),当停止工作时,油箱中油量为 10 升.在整个过程中,油箱里的油量 y(单位:
升)与时间 x(单位:分)之间的关系如图所示.
(1)机器加.油.过.程.中每分钟加油量为 升,机器加.工.过.程.中每分钟耗油量
为 升.
(2)求机器加.工.过.程.时 y 关于 x 的函数解析式;
(3)当油箱中油量为油箱容积的一半时,直接写出 x 的值.
y (升)
90
10
O 10 90 x (分)
第4页(共 8 页)
21.如图,在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,延长 CB 到点 E,使BE = BC,
连接 AE .
(1)求证:四边形 AEBD 是平行四边形;
(2)若 CD=13,AC=10,求 AE 的值.
A D
O
E
B C
22.在平面直角坐标系 xOy 中,一次函数 y kx+b(k≠0)的图象,由函数 y=x 的图
象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当 x >1 时,对于 x 的每一个值,函数 y m(x m 0)的值大于一次函数
y kx+b 的值,直接写出 m 的取值范围.
y
4
3
2
1
–4 –3 –2 –1 O 1 2 3 4 x
–1
–2
–3
23.一次函数 y = kx+1(k ≠ 0)的图象过点 P(-3,2),与 x 轴交于点 A,与 y 轴交于点
B.
(1)求 k 的值及点 A、B 的坐标;
(2)已知点 C(-1,0),若以 A,B,C,D 为顶点的四边形是平行四边形,请直接写
出所有符合条件的点 D 的坐标.
第5页(共 8 页)
24.如图,在菱形 ABCD 中,∠B=60°,AB=1,延长 AD到点 E,使 DE=AD,延长 CD 到
点 F,使 DF=CD,连接 AC、CE、EF、AF.
(1)求证:四边形 ACEF 是矩形;
(2)求四边形 ACEF 的周长.
A F
D
B
C E
25.如图,在平面直角坐标系 xOy 中,直线 l1经过原点,且与直线 l2:y=-x+3 交于
点 A(m,2),直线 l2与 x 轴交于点 B.
(1)求直线 l1 的函数解析式;
(2)点 P(n,0)在 x 轴上,过点 P 作平行于 y 轴的直线,分别交直线 l1与直线 l2 于点
M、N,若 MN=OB,求 n 的值.
26.如图,将矩形纸片 ABCD 沿过点 A 的直线翻折,点 B 恰好与其对角线 AC 的中点 O
重合,折痕与边 BC 交于点 E. 延长 EO 交 AD 于点 F,连接 CF.
(1)按要求补全图形;
(2)求证:四边形 AECF 是菱形;
A D
(3)若 AB= 6 ,求 BE 的长.
O
B E C
第6页(共 8 页)
27.如图,在正方形 ABCD 中,点 E 是边 AB 上的一动点(不与点 A、点 B 重合),连接
DE,点 A 关于直线 DE 的对称点为 F,连接 EF 并延长交 BC 边于点 G,连接 DF,
DG.
(1)依题意补全图形,并证明∠FDG=∠CDG;
(2)过点 E 作 EM⊥DE 于点 E,交 DG 的延长线于点 M,连接 BM.用等式表示
线段 AE,BM 的数量关系,并证明.
A D
E
F
B C
28.对于两个实数 a,b,规定 Max(a,b)表示 a,b 两数中较大者,特殊地,当 a = b
时,Max(a,b)=a.如:Max(1,2)= 2,Max(-1,-2)= -1,Max(0,0)=
0.
(1)Max(-1,0)= ,Max(n,n -2)= ;
(2)对于一次函数 y1 = x 2, y2 = x +b,
①当 x≥-1 时,Max(y1,y2)= y2,求 b 的取值范围;
②当 x=1-b 时,Max(y1,y2)=p,当 x=1+b 时,Max(y1,y2)=q,若
p≤q,直接写出 b 的取值范围.
第7页(共 8 页)
以下为草稿纸
第8页(共 8 页)
同课章节目录
