人教版九年级数学下册 第27章 相似 全章知识点复习题 (含解析)
文档属性
| 名称 | 人教版九年级数学下册 第27章 相似 全章知识点复习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 07:06:00 | ||
图片预览




文档简介
第27章《相似》全章知识点复习题
【题型1 成比例线段的计算】
1.已知线段a、b满足,且.
(1)求线段a、b的长;
(2)若线段c是线段a、b的比例中项,求线段c的长.
2.如果地图上、两处的图距是,表示这两地的实际距离是,那么实际距离是的两地在地图上的图距是 .
3.已知线段,,,是成比例线段,其中,,,则的值是 .
4.巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽.
(1)黄金矩形的长 ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形,得到新的矩形,猜想矩形是否为黄金矩形,并证明你的结论;
(3)在图②中,连接,求点到线段的距离.
【题型2 比例性质的应用】
1.已知,则( )
A.1 B. C.1或 D.2
2.若,a,c不为零则下列等式中不一定成立的是( )
A. B. C. D.
3.已知,,均为非零的实数,且满足,则的值为 .
4.已知满足,试求的最大值 .
【题型3 平行线分线段成比例的应用】
1.如图,已知直线,直线m与直线、、分别交于点A、D、F,直线n与直线、、分别交于点B、C、E.若,则 .
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段的长是( )
A. B. C. D.
3.如图,在中,,,与相交于点,则 .
4.在边长为1的等边三角形中,D为直线上一点,,点E在直线上,且,则的长为 .
【题型4 相似三角形的判定】
1.如图,在中,点E为边上一点,连结:点F为线段上一点,且.求证:.
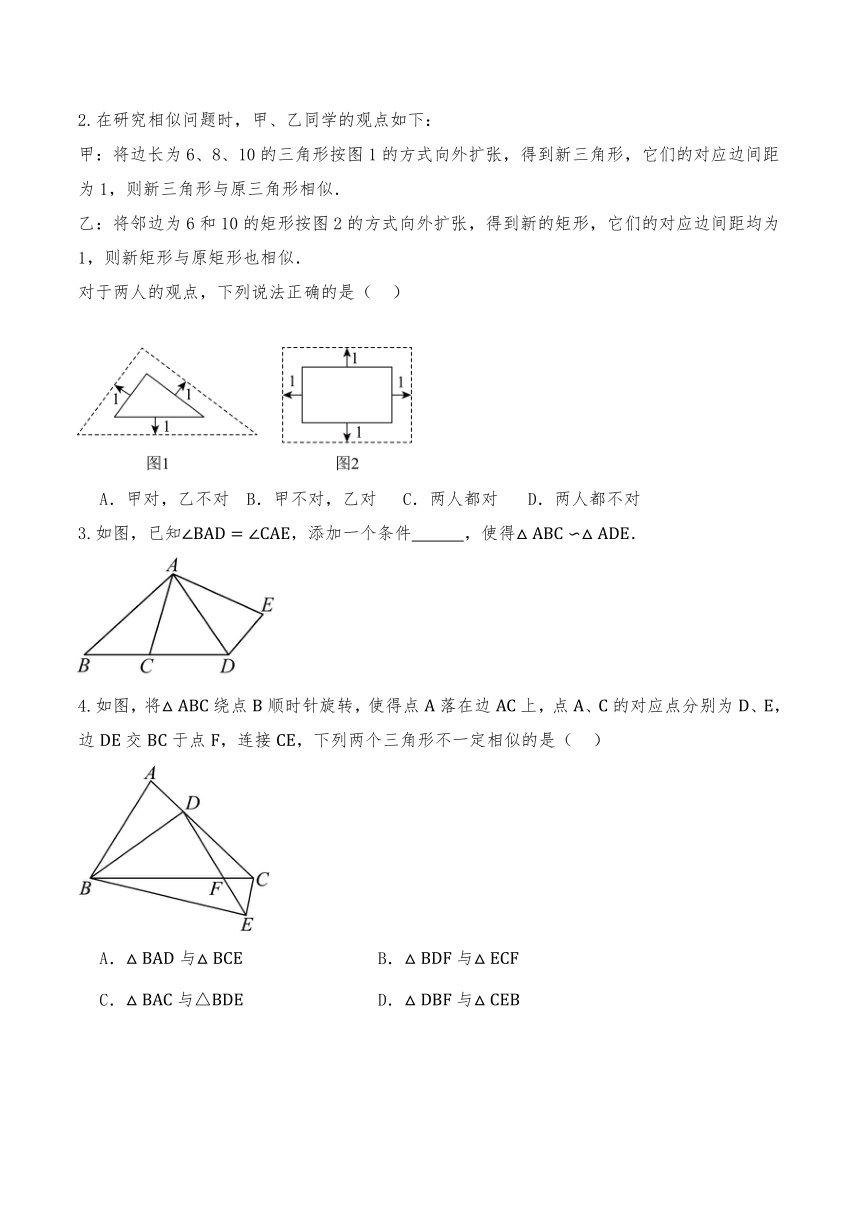
2.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为6、8、10的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为6和10的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形也相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
3.如图,已知,添加一个条件 ,使得.
4.如图,将绕点顺时针旋转,使得点落在边上,点、的对应点分别为、,边交于点,连接,下列两个三角形不一定相似的是( )
A.与 B.与
C.与 D.与
【题型5 利用相似三角形的性质求值】
1.某公园的儿童游乐场是两个相似三角形地块,相似比为,面积差为30,则它们的面积和为( )
A.74 B.76 C.78 D.81
2.如图,则下列式子中不成立的是( )
A. B. C. D.
3.若与相似,已知,,,则 .
4.若三角形三边的长度之比为4:4:7,与它相似的三角形的最长边为,则最短边为 .
【题型6 与相似多边形有关的计算】
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
2.如图,在菱形中,,点E、F是对角线上的点(点E、F不与B、D重合),分别连接若四边形是菱形,且与菱形是相似菱形,那么菱形的边长是 .(用a的代数式表示).
3.如图所示的四边形,与选项中的四边形一定相似的是( )
A. B.
C. D.
4.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
【题型7 网格中相似三角形的相关计算】
1.图①、图②、均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)在图①的网格中确定一点D,连结,使与全等.(画出两个)
(2)在图②中的边上确定一点E,连结,使 ;
(3)在图③中的边上确定一点P,在边上确定一点Q,连结,使 ,且相似比为.
2.以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上.
(1)在图1中,________;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图2,在线段上找一点P,使;
②如图3,在线段上找一点P,使.
3.如图,在由若干个小正方形组成的网格图中,的顶点均在格点上.请仅用无刻度的直尺完成以下作图(保留作图痕迹,不写作法).
(1)在图中的外部作,使;
(2)在图中,作绕点顺时针旋转一定角度后,各个顶点仍在格点上的.
4.图①、图②、图③均是的正方形网格,每个小正方形的边长均为,其顶点称为格点,的顶点均在格点上,只用无刻度的直尺.在给定的网格中,按下列要求作图,保留作图痕迹,并完成填空.
(1)在图①中的边上确定一点,连结,使.直接写出与的相似比为______;
(2)在图②中的边上确定一点,在边上确定一点,连结,使,且相似比为.直接写出______;
(3)在图③中的边上确定一点,在边上确定一点,连结,使且相似比为.直接写出的长度为______.
【题型8 相似三角形的判定与性质的综合应用】
1.如图,在正方形中,,点E是边上一点,且,点F是上一点,若,则的长为( )
A. B. C. D.
2.如图,在四边形ABCD中,,O是对角线的中点,连结并延长交边或边于点E.
(1)当点E在上,
①求证:;
②若,求的值;
(2)若,直接写出的长.
3.如图,在中,,为的角平分线,点在的延长线上,于点,点在上,,连接交于点.若点是的中点,则的值为 .
4.如图,正方形的边长为4,E是边的中点,点P在射线上,过P作于F,设.
(1)求证:;
(2)当P也是边中点时,求的值;
(3)若以P,F,E为顶点的三角形也与相似,试求x的值;
(4)当点F与点E重合时,设交于点G,试判断与的大小关系并说明理由.
【题型9 与判定相似三角形中等积式的证明】
1.如图,在四边形中,,点在边上,连接、,满足,且.
(1)求证:四边形是等腰梯形;
(2)当时,求证;.
2.如图,在平行四边形中,点在边上,交于点,.
(1)求证:;
(2)如果.
①求的长;
②若,求的长.
3.如图,矩形中,,,点是边上的任意一点(不与端点,重合),连接,且交于点.
(1)求证:;
(2)若点也在上,满足,如图所示.求证:.
4.如图,,,.
(1)如图1,不添加辅助线,请写出图中所有相似三角形;
(2)如图2,若点E落在边上,求证:;
(3)如图3,若点H,I,J分别为,,中点,判断与的数量关系及夹角度数(锐角).
【题型10 相似三角形中的运动问题】
1.如图,四边形中,,,,,,动点P从点A出发以1个单位/秒的速度沿运动,动点Q同时从点C出发以2个单位/秒的速度沿运动,过点P作,交于E,连接,当点Q与B重合时,两动点均停止运动,设运动时间为t秒.
(1)当时,求线段的长;
(2)当运动t秒时线段的长(用含t的式子表示);
(3)运动过程中是否存在某一时刻,使与相似?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
2.如图,在中,,,,点从点开始向点以的速度移动,点从点开始沿边向点以的速度移动,当、两点中有一点到达终点时,则同时停止运动.
(1)如果、分别从、同时出发,那么经过几秒时,的面积等于?
(2)如果、分别从、同时出发,那么经过几秒时,的长度等于?
(3)几秒钟后,与相似?
3.如图,的两条直角边,,点D沿从A向B运动,速度是/秒,同时,点E沿从B向C运动,速度为/秒.动点E到达点C时运动终止.连接、、.
(1)当动点运动时间 秒时,与相似.
(2)在运动过程中,当时,为何值?请说明理由.
4.已知矩形中,,点是对角线上一点,且.点是边中点,点从点出发,沿方向运动,速度为cm/s,点从点出发,沿方向运动,速度为cm/s,两点同时开始运动,运动的时间为.若面积记为,面积记为,面积记为.当点运动到点的正上方时,两点运动停止.
(1)如图①,点在线段(包含端点)上运动时,与的函数图像如图②所示,则的长为___________cm;
(2)如图③,点在线段上运动;
①若,求此时的值;
②若,求此时的值.
【题型11 利用相似三角形测物体的高度】
1.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图),已知小明的眼睛离地面米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为米,小亮身高米,请根据以上数据求出城楼的高度.
2.如图,屋架跨度的一半,高度.现要在屋顶上开一个天窗,在水平位置,且.求天窗高度的长.
3.用手举一根标尺,让标尺与地面垂直,调整人与旗杆的距离或人与标尺的距离,使标尺刚好挡住旗杆,此方法可测量旗杆的高度. 若人与标尺的水平距离,人与旗杆的水平距离,标尺的长度,根据测量结果,试求旗杆的高度.
4.某学校数学课外活动小组测量校园内一棵树的高度.采用的方法如下:如图,首先把支架放在离树适当距离的水平地面上点处,再把镜子水平放置在支架上点处,然后观测者沿着直线后退至点处,这时恰好在镜子里看到树的顶端.用皮尺分别测得,.若观测者目高为,支架的高为,求这棵树的高度.
【题型12 影子部分不落在地面上求物体的高度】
1.如图,在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同一时刻旗杆的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上影长为米,留在墙上的影长米,则旗杆的高度( )
A.8米 B.9米 C.10米 D.10.2米
2.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为 .
3.小明和爸爸在公园散步,此时爸爸的影子落在了身后的地面和墙上,如图1所示.其中,段为地上的影子,段为墙上的影子.小明想利用所学知识测量出爸爸的身高.他向工作人员询问得知:公园地面与墙面所用均为厚度,长度的砖块,小明数了一下,段刚好是4块地砖的长度,而段恰好为4块地砖的厚度;同一时刻,小明观察到公园门口指示牌影子的顶端刚好到达保安亭,如图2所示,其中为指示牌的影子.已知爸爸、墙面、指示牌和保安亭均与地面垂直,指示牌高,指示牌距保安亭,请你根据以上信息,帮小明求出爸爸的身高.
4.物体在太阳光线的照射下会留下“影子”,某兴趣小组在利用影子测量物体的高度时,甲同学测得一根长为1米的垂直于地面的标杆,在地面上的影长为米,请解答下列问题.
(1)如图1,乙同学测得旗杆在地面上的影长为6米,那么旗杆的高度为 米.
(2)如图2,丙同学想测量一棵树的高度,他发现树的影子落在了地上和墙上,地面上的影长为3米,墙上的影长长为1米,则树的高度为多少?
(3)如图3,丁同学想测量一根电线杆的高度,他发现电线杆的影子恰好落在地面和一斜坡上,测得地面上的影长为4米,坡面上的影长为2米,已知斜坡的坡角为,则电线杆的高度是多少?
【题型13 位似图形】
1.在下列四个三角形中,与是位似图形且为位似中心的是( )
A.① B.② C.③ D.④
2.如图,在正方形网格中,与位似,则下列说法正确的是( )
A.位似中心是点D B.位似中心是点G
C.位似比为 D.位似比为
3.如图,已知ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=AO,OE=BO,OF=CO,得DEF.下列说法中,错误的是( )
A.DEF与ABC是位似三角形 B.OAC与ODF是位似三角形
C.DEF与ABC周长的比是1:3 D.图中位似的两个三角形面积比是1:9
4.如图,已知的面积为24,以B为位似中心,作的位似图形,位似图形与原图形的位似比为,连接AG、DG.则的面积为 .
【题型14 位似变换作图与计算】
1.如图,在正方形网格图中,每个小正方形边长均为1,点和的顶点均为小正方形的顶点.
(1)以为位似中心,在网格图中作,使和位似,且位似比为.
(2)证明和相似.
2.如图,的顶点都在网格点上,点A的坐标为.
(1)以点O为位似中心,把按放大,在y轴的左侧,画出放大后的;
(2)点A的对应点D的坐标是______;
(3) ______.
3.在如图所示的正方形网格中,建立平面直角坐标系,的三个顶点的坐标分别为,,.
(1)画出关于原点对称的,并分别写出的坐标;
(2)在网格内,画出以点为位似中心,把放大为原来的倍后的;
(3)若也是的位似图形,点是位似中心,在图中画出点.
4.已知在平面直角坐标系中的位置如图所示:
(1)在图中画出沿x轴翻折后的;
(2)以点为位似中心,作出按放大后的位似图形;
(3)点的坐标___________;与的周长比是___________,与的面积比是___________.
参考答案
【题型1 成比例线段的计算】
1.(1)解:,
设,,
,
,
,
,,
线段的长为18,线段的长为12.
(2)解:线段是线段、的比例中项,,,
,
由题意知,,
,
线段的长为.
2.10
【分析】先设这个图距是,根据图上距离比上实际距离等于比例尺,可得关于的方程,即可求解.
【详解】设这个图距是,
则4:20000000=x:50000000,
解得x=10.
故填:10.
3.
【分析】本题主要考查了比例线段,熟练掌握比例线段的性质是解题的关键.根据比例线段的定义得到,即可得到答案.
【详解】解:由于线段,,,是成比例线段,
故,
即
解得
故答案为:.
4.(1)解:∵,,
∴,
故答案为:;
(2)解:矩形为黄金矩形,理由是:
由(1)知,
∴,
∴,
故矩形为黄金矩形;
(3)解:连接,,过D作于点G
∵,,
∴,
在中, ,
即,
则,
解得,
∴点D到线段的距离为.
【题型2 比例性质的应用】
1.C
【分析】本题考查了比例的性质,熟悉等比性质是解题的关键.分两种情况进行讨论:①当时,根据等比性质计算得出结果;②当时,则,代入计算得出结果.
【详解】解:分两种情况:
①当时,得;
②当时,
则,;
综上所述,k的值为1或.
故选:C.
2.D
【分析】本题主要考查比例性质的变形,根据比例的性质,对所给选项进行整理,找到不一定成立的选项即可
【详解】解:A.∵,∴,正确,不符合题意;
B. ∵,∴,∴,正确,不符合题意;
C. ∵,∴,∴,∴,∴,正确,不符合题意;
D.当时,原式不成立,故选项D符合题意,
故选:D
3.或
【分析】根据题意得出,三式相加得出,然后分类讨论,即可求解.
【详解】解:∵,
∴
∴
即,
当时,,
当时,,
故答案为:或.
4.25
【分析】设,得到关于k的等式,利用配方法和非负数的性质即可求解.
【详解】解:设,
∴a-1=2k,b+1=3k,c-2=4k,即a=2k+1,b=3k-1,c=4k+2,
∴a2+b2 c2= (2k+1)2+(3k-1)2 (4k+2)2
=4k2+4k+1+9k2-6k+1-(16k2+16k+4)
=4k2+4k+1+9k2-6k+1-16k2-16k-4
=-3k2-18k-2
=-3(k2+6k+9-9)-2
=-3(k+3) 2+25
∵(k+3) 2≥0,则-3(k+3) 2≤0,
∴a2+b2 c2的最大值为25,
故答案为:25.
【题型3 平行线分线段成比例的应用】
1.
【分析】根据平行线分线段成比例定理得出比例式,解答即可.
【详解】解:直线,
,
,
故答案为:.
2.C
【分析】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,根据平行线分线段 成比例定理列出比例式,计算即可.
【详解】解:过点作平行横线的垂线,交点所在的平行横 线于,交点所在的平行横线于,
∵五线谱是由等距离、等长度的五条平行横线组成的,
∴,
∴,
解得:,
故选:C.
3.
【分析】先过E作,交于G,再作交于H,由平行线分线段成比例定理的推论,再结合已知条件,可分别求出和的值,相加即可.
【详解】解:作交于,作交于,如图所示:
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故答案为:.
4.或3
【分析】分点在线段的延长线和反向延长线上,两种情况进行讨论求解即可,当点在线段的延长线上时,推出为等腰三角形,三角形外角的性质求出,根据等边对等角,推出为含30 度角的直角三角形,求出的长,进而求出的长即可,当点在线段的反向延长线上时,过点作,过点作,得到,根据等边三角形和等腰三角形的性质,结合平行线分线段成比例进行求解即可.
【详解】解:当点在的延长上时,如图,
∵边长为1的等边三角形,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
当点在的反向延长上时,如图,
过点作,过点作,
则:,
∵为等边三角形,,
∴,
∵,
∴,
∴,
∴,
∴;
综上:或;
故答案为:或3.
【题型4 相似三角形的判定】
1.证明:在中,,
∴,
∵,
∴,
∵,,
∴,
∴.
2.A
【分析】本题考查相似三角形的判定、相似多边形的判定,根据题意得,,,,可得,,即可证得;再根据题意得,,可得,可知新矩形与原矩形不相似,即可求解.
【详解】解:甲:根据题意得,,,,
∴,,
∴,
∴甲说法正确;
乙:根据题意得,,,则,,
∴,,
∴,
∴新矩形与原矩形不相似,
∴乙说法不正确;
故选:A.
3.(答案不唯一)
【分析】本题考查了相似三角形的判定,根据相似三角形的判定推理即可;熟练掌握相似三角形的判定是解题的关键.
【详解】解:由可得,
根据相似三角形的判定,可添加一个角或的两边对应成比例;
故可以添加:或或;
故答案为:(答案不唯一)
4.D
【分析】本题考查了相似三角形的判定、旋转的性质等知识,根据旋转的性质得到,,,,,再根据相似三角形的判定定理判断求解即可.
【详解】解:根据旋转的性质得,,
∴,
∴,,
∴,故A不符合题意;
∵,
∴,
∴,
又∵,
∴,故B不符合题意;
又,,
∴,故C不符合题意;
根据题意,无法求解与相似,
故D符合题意;
故选:D.
【题型5 利用相似三角形的性质求值】
1.C
【分析】本题主要考查了对相似三角形性质的理解,解题的关键是掌握相似三角形面积比与相似比之间的关系,即相似三角形面积比等于相似比的平方.
已知两相似三角形的相似比,即可求出面积比.根据面积差为30,可求出两三角形的面积,进而可求出面积和.
【详解】解:∵两三角形的相似比为,
∴它们的面积比为,
设较小三角形的面积为,则较大三角形的面积为,
则,
解得,
∴面积和为,
故选C.
2.D
【分析】本题考查了相似三角形的性质,根据相似三角形的性质得出,逐项分析判断,即可求解.
【详解】解:∵
∴
∴,故A,B,C正确,D错误
故选:D.
3.
【分析】本题主要考查了相似三角形的性质,解分式方程等知识点,熟练掌握相似三角形的性质是解题的关键.
三角形相似,对应边成比例,据此即可求出答案.
【详解】解:,
,
,,,
,
解得:,
经检验,是原分式方程的根,
故答案为:.
4.12
【分析】本题考查相似三角形的性质,关键是设出与它相似的三角形的三边,利用最长边构造方程.
根据相似三角形的性质,依题意设这个三角形三边为,确定,即可得出最短边长.
【详解】解:∵三角形三边之比为4:4:7,
∴与他相似的三角形的三边之比也为4:4:7,
设这个三角形三边为,
∵与它相似的三角形的最长边为,
∴,
则,
最短边长为,
故答案为:12.
【题型6 与相似多边形有关的计算】
1.B
【分析】根据对折表示出小长方形的长和宽,再根据相似多边形的判定,对应边成比例列式计算即可.
【详解】解:对折两次后的小长方形的长为b,宽为,
要使小长方形与原长方形相似,只要满足即可,
∴.
故选:B.
2.
【分析】连接,根据菱形对角线互相垂直,构建直角三角形,再根据相似,得出,再根据直角三角形30°角所对的边是斜边的一半得出,最后根据勾股定理求解即可.
【详解】解:连接,
∵四边形为菱形,,
∴,,
∴,
∵菱形与菱形相似,
∴,
∴,
∴,
根据勾股定理可得:,
即,解得:.
故答案为:.
3.D
【分析】根据勾股定理求出四边形ABCD的四条边之比,根据相似多边形的判定方法判断即可.
【详解】作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
4.(1)设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
【题型7 网格中相似三角形的相关计算】
1.(1)解:如图中,点中任取两个即为所求;
(2)解:如图中,点E即为所求;
由图可知,,
,
又,
,
是直角三角形,
∴,
又∵,
∴;
(3)解:如图,取格点,连接,交于点,点P,点Q即为所求,
如图:,
四边形是平行四边形,
,
则:,
∴,
相似比为:.
2.(1)解:由图得,
,,
,
,
故答案:;
(2)解:①如图,
点为所求;
②如图,
点为所求.
3.(1)解:如图所示,即为所求.
理由:∵,,
∴,
又∵,
∴;
(2)解:如图所示,即为所求.
4.(1)解:根据题意,作图如下:
,
,
,
,
,
故取格点,格点,连接,
,
,
相似比为:,
即为所求,
故答案为:;
(2)根据题意得:
,且相似比为,作图如下:
,
取格点,格点,连接,交于点,则,
即为所求,
由(1)得,
又相似比为,
,
,
故答案为:.
(3)根据题意得,
且相似比为,
,
,
,
取格点,格点,连接,交于点,则,
即为所求,
,
又,
,
故答案为:.
【题型8 相似三角形的判定与性质的综合应用】
1.B
【分析】本题主要考查了正方形的性质,勾股定理,相似三角形的性质与判定,由正方形的性质得到,,则由勾股定理得到,求出,则,再证明,得到,即,即可得到.
【详解】解:如图所示,连接
∵四边形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴
∵,
∴,
又∵,
∴,
∴,即,
∴,
故选:B.
2.(1)①证明:如图1,
∵,
∴,
∵,
∴
∵是斜边上的中线,
∴,
∴,
∴,
∴,
∴,
∵,
∴,即,
∴,
∴;
②解:如图2, 若,
在中,,
∴,
过点D作于点H,设,则,在中,,
∴,
∴,
;
(2)解:如图3,当点E在上时,
设则设
,
把代入中,得:
,
解得:, (舍去) ,
如图4, 当点E在上时,
,
∴四边形是矩形,
设
∵
∴
∵,
∴,
在中,由勾股定理得
在中, 由勾股定理得
∴解得:,(舍去)
,
综上所述,的长为:或 .
3.
【分析】本题主要考查相似三角形的判定和性质,全等三角形的判定和性质,证明是解题的关键.
先证明,可得,进而得到,从而证得,可得,进而即可求解.
【详解】解:∵,
∴,
∵,,
∴,
∴
∵,,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴设,,
∵H是的中点,
∴,
∴,
∵,
∴,
∴,
∵,
∴=.
故答案是:.
4.(1)∵四边形是正方形,
∴,,
∴,.
又∵,
∴,
∴;
(2)当P是的中点时,.
∵,
∴,即,
∴;
(3)分两种情况:
①当,且时,则有,
∴四边形为矩形,
∴,即.
②当,且时.
∵,
∴,
∴.
∵,
∴点F为的中点.
∵,
∴
,即,
∴,
∴,即;
∴满足条件的x的值为2或5;
(4).理由如下:
如图,∵四边形是正方形,
∴,,
∴.
∵E是的中点,
∴,
∴.
∵,
∴,,
∴,
∴,
∴,即,
∴,
∴
,
∴.
又∵,
∴,
∴.
【题型9 与判定相似三角形中等积式的证明】
1.(1)证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴四边形是等腰梯形;
(2)证明:∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
2.(1)证明:四边形是平行四边形
,
,
.
,即.
(2)①解:
,即
,
解得:(舍去负值)
②解:
,
3.(1)证明:四边形是矩形,
,
,
,
,
,
,
,
,
;
(2)证明:四边形是矩形,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
故.
4.(1)解:∵,,,
∴,
又∵,
∴,
同理可得:,;
(2)证明:∵,,
∴,
∴,即,
又∵,,
∴;
(3)解:连接,设直线和交于点K,
∴,
∴,
设,,则,,
∵点H,I,J分别为,,中点,
∴,,,
∴,,即,
∴,
∴,,
∴,
∴,
∴.
【题型10 相似三角形中的运动问题】
1.(1)当时,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(2)由运动知,,
∵,
∴,
∴,
∴,
由运动知,,
∴,
在中,,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵,
∴,
若,,
∴,
∵,
∴,
∴(不合题意舍去),
若,,
∴,
∴,
∴.
故当时,与相似.
2.(1)解:设经过秒以后,面积为()
此时,,,
由,得,
整理得:,
解得:,(舍).
(2)解:设经过秒后,的长度等于,
由,得,
解得:(舍去),.
答:2秒后,的长度为.
(3)解:当时,
即,解得
当时,
,
即,
解得,
或.
3.(1)解:设经过运动时间为t秒时,与相似.
则,,, ;
1)当,即时,
;
,即,
.
2)当,即时,
,
,即,
.
和都符合,
当动点运动秒或秒时,与相似.
故答案为:或.
(2)如图,过点E作于F,
设经过运动时间为t秒时,,
则,,, ;
,即,
,,
,
,
,
,
,
,
,
,
,
,即,
(秒).
4.(1)解:由图②可知,
当x的值为时,点运动到了点,
∴,
故 (cm)
(2)解:①如图3,过点作于点
∵,
∴,
∵,
∴
在Rt中,
∴
解得:
∵点在线段上运动,
∴,
∴此时的值为3秒.
②如图3,过点作,交于点, 交于点
由题意得:,
∴,
∵,
∴,
∴,解得,
同理,
可得,
∵
∴,
∵
∴,
∴
解得:
∵,
∴此时的值为秒.
【题型11 利用相似三角形测物体的高度】
1.解:如图,过点作于点,交于点,
依题意,,
∴,
∵,
∴,
∴,
即,
解得:,
∵,
∴城楼的高度为米
2.解:由题意得,
,
又,
,
,
,
天窗高度的长.
3.解:由题意可知,
∴,,
∴,,
∴,
∵,,,则,
∴,
即:旗杆的高度为.
4.解:过点作水平线交于点,交于点,由是水平线,都是铅垂线,则四边形是矩形,四边形是矩形,如图,
,,,
,
又根据题意,得, ,
,
,即 ,
解得:,
,
答:这棵树的高度为.
【题型12 影子部分不落在地面上求物体的高度】
1.A
【分析】本题考查了相似三角形的应用,作于点,如图,则四边形为矩形,,,利用“在同一时刻物高与影长的比相等得到” ,求出从而可得到的长.
【详解】作于点,如图,
则四边形为矩形,,,
根据题意得,
即,
解得,
所以.
答:旗杆的高度为米.
故选:A.
2.4米
【分析】根据同一时刻物高与影长成正比例列式计算即可.
【详解】如图,设树高为AB,过点C作CD⊥AB于D,则CD=1.1+1.6=2.7米,DB=1米,
∵同一时刻物高与影长成正比例,
∴,
解得:AD=3,
∴AB=AD+DB=3+1=4(米).
故答案为:4米.
3.解:如图:过点作,垂足为,
由题意得:,,
指示牌高,指示牌距保安亭,
,
,
,
爸爸的身高为.
4.(1)解:∵一根长为1米的垂直于地面的标杆,在地面上的影长为米,
∴旗杆在地面上的影长为6米,旗杆的高度为12米,
故答案为:12;
(2)解:如图2,连接并延长,交直线于点H,
米,
米,
米,则,
解得:,
答:树的高度为7米;
(3)解:如图3,连接并延长,交直线于点C,过点K作于点N,
在中,米,,
则米,米,
由题意得:米,
米,
则,
解得:米,
答:电线杆的高度是米.
【题型13 位似图形】
1.B
【分析】根据位似图形的概念判断即可.
【详解】解:∵②与△ABC相似,对应点的连线相交于点O,对应边互相平行,
∴②与△ABC是位似图形且O为位似中心,
故选:B.
2.C
【分析】本题考查正方形的性质、位似图形,如果两个图形不仅是相似图形,而且对应顶点的连线所在直线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.掌握位似图形的意义与位似比求法是解题的关键.连接、、,可知位似中心在点,之间,根据两个三角形网格数可知相似比,即可得出结论.
【详解】解:如图,连接、、,
在正方形网格中,与位似,点是的中点,
位似中心在点,之间,,故选项A,B错误,
相似比为,
位似比为,故选项正确,D错误,
故选:.
3.D
【分析】根据位似三角形的定义及性质即可判断.
【详解】A、由题意知,△DEF与△ABC是位似三角形,故正确;
B、由题意知,△OAC与△ODF是位似三角形,故正确;
C、由于△DEF与△ABC是位似三角形,因而也是相似三角形,且相似比为1:3,从而周长的比也为1:3,故正确;
D、此选项没有指明是哪两个位似三角形,故错误.
故选:D.
4.4
【分析】延长EG交CD于点H,由题意可得四边形AEHD是平行四边形,则可得此平行四边形的面积为8,从而可得△ADG的面积.
【详解】延长EG交CD于点H,如图,
∵四边形ABCD是平行四边形,四边形EBFG是平行四边形,
∴AB∥CD,AD∥BC;BF∥EG,
∴AD∥EG,
∴四边形AEHD是平行四边形,
∴.
∵位似图形与原图形的位似比为,
∴,
即,
∴,
∴.
故答案为:4.
【题型14 位似变换作图与计算】
1.(1)解:如图所示:即为所求,
;
(2)证明:小正方形边长为1,
,,,,,,
,,,
∴,
∴.
2.(1)解:位似中心为点,位似比,已知,,,
∴对应点的坐标分别是,,,
连接点,如图所示,
;
(2)由(1)知,
故答案为:;
(3)如图,连接,,
,
,
,
∴,
∴设,则,
∴,
故答案为:.
3.(1)如图,,,关于原点对称,,,连接,
∴即为所求;
(2)如图,延长,,然后连接,
∴即为所求;
(3)如图,连接,相交于点,
∴点即为所求.
4.(1)解:如图,为所作;
(2)解:如图,为所作;
(3)解:点的坐标为,
∵沿x轴翻折后的,
∴,
∵按放大后的位似图形,
∴与的相似比为,
∴与的相似比为,
∴与的周长的比为,与的面积的比为.
故答案为:;;
【题型1 成比例线段的计算】
1.已知线段a、b满足,且.
(1)求线段a、b的长;
(2)若线段c是线段a、b的比例中项,求线段c的长.
2.如果地图上、两处的图距是,表示这两地的实际距离是,那么实际距离是的两地在地图上的图距是 .
3.已知线段,,,是成比例线段,其中,,,则的值是 .
4.巴台农神庙的设计代表了古希腊建筑艺术上的最高水平,它的平面图可看作宽与长的比是的矩形,我们将这种宽与长的比是的矩形叫黄金矩形.如图①,已知黄金矩形的宽.
(1)黄金矩形的长 ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以为边的正方形,得到新的矩形,猜想矩形是否为黄金矩形,并证明你的结论;
(3)在图②中,连接,求点到线段的距离.
【题型2 比例性质的应用】
1.已知,则( )
A.1 B. C.1或 D.2
2.若,a,c不为零则下列等式中不一定成立的是( )
A. B. C. D.
3.已知,,均为非零的实数,且满足,则的值为 .
4.已知满足,试求的最大值 .
【题型3 平行线分线段成比例的应用】
1.如图,已知直线,直线m与直线、、分别交于点A、D、F,直线n与直线、、分别交于点B、C、E.若,则 .
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段的长是( )
A. B. C. D.
3.如图,在中,,,与相交于点,则 .
4.在边长为1的等边三角形中,D为直线上一点,,点E在直线上,且,则的长为 .
【题型4 相似三角形的判定】
1.如图,在中,点E为边上一点,连结:点F为线段上一点,且.求证:.
2.在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为6、8、10的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为6和10的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形也相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
3.如图,已知,添加一个条件 ,使得.
4.如图,将绕点顺时针旋转,使得点落在边上,点、的对应点分别为、,边交于点,连接,下列两个三角形不一定相似的是( )
A.与 B.与
C.与 D.与
【题型5 利用相似三角形的性质求值】
1.某公园的儿童游乐场是两个相似三角形地块,相似比为,面积差为30,则它们的面积和为( )
A.74 B.76 C.78 D.81
2.如图,则下列式子中不成立的是( )
A. B. C. D.
3.若与相似,已知,,,则 .
4.若三角形三边的长度之比为4:4:7,与它相似的三角形的最长边为,则最短边为 .
【题型6 与相似多边形有关的计算】
1.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是( )
A.a=b B.a=2b C.a=2b D.a=4b
2.如图,在菱形中,,点E、F是对角线上的点(点E、F不与B、D重合),分别连接若四边形是菱形,且与菱形是相似菱形,那么菱形的边长是 .(用a的代数式表示).
3.如图所示的四边形,与选项中的四边形一定相似的是( )
A. B.
C. D.
4.为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
【题型7 网格中相似三角形的相关计算】
1.图①、图②、均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)在图①的网格中确定一点D,连结,使与全等.(画出两个)
(2)在图②中的边上确定一点E,连结,使 ;
(3)在图③中的边上确定一点P,在边上确定一点Q,连结,使 ,且相似比为.
2.以下各图均是由边长为1的小正方形组成的网格,图中的点A、B、C、D均在格点上.
(1)在图1中,________;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图2,在线段上找一点P,使;
②如图3,在线段上找一点P,使.
3.如图,在由若干个小正方形组成的网格图中,的顶点均在格点上.请仅用无刻度的直尺完成以下作图(保留作图痕迹,不写作法).
(1)在图中的外部作,使;
(2)在图中,作绕点顺时针旋转一定角度后,各个顶点仍在格点上的.
4.图①、图②、图③均是的正方形网格,每个小正方形的边长均为,其顶点称为格点,的顶点均在格点上,只用无刻度的直尺.在给定的网格中,按下列要求作图,保留作图痕迹,并完成填空.
(1)在图①中的边上确定一点,连结,使.直接写出与的相似比为______;
(2)在图②中的边上确定一点,在边上确定一点,连结,使,且相似比为.直接写出______;
(3)在图③中的边上确定一点,在边上确定一点,连结,使且相似比为.直接写出的长度为______.
【题型8 相似三角形的判定与性质的综合应用】
1.如图,在正方形中,,点E是边上一点,且,点F是上一点,若,则的长为( )
A. B. C. D.
2.如图,在四边形ABCD中,,O是对角线的中点,连结并延长交边或边于点E.
(1)当点E在上,
①求证:;
②若,求的值;
(2)若,直接写出的长.
3.如图,在中,,为的角平分线,点在的延长线上,于点,点在上,,连接交于点.若点是的中点,则的值为 .
4.如图,正方形的边长为4,E是边的中点,点P在射线上,过P作于F,设.
(1)求证:;
(2)当P也是边中点时,求的值;
(3)若以P,F,E为顶点的三角形也与相似,试求x的值;
(4)当点F与点E重合时,设交于点G,试判断与的大小关系并说明理由.
【题型9 与判定相似三角形中等积式的证明】
1.如图,在四边形中,,点在边上,连接、,满足,且.
(1)求证:四边形是等腰梯形;
(2)当时,求证;.
2.如图,在平行四边形中,点在边上,交于点,.
(1)求证:;
(2)如果.
①求的长;
②若,求的长.
3.如图,矩形中,,,点是边上的任意一点(不与端点,重合),连接,且交于点.
(1)求证:;
(2)若点也在上,满足,如图所示.求证:.
4.如图,,,.
(1)如图1,不添加辅助线,请写出图中所有相似三角形;
(2)如图2,若点E落在边上,求证:;
(3)如图3,若点H,I,J分别为,,中点,判断与的数量关系及夹角度数(锐角).
【题型10 相似三角形中的运动问题】
1.如图,四边形中,,,,,,动点P从点A出发以1个单位/秒的速度沿运动,动点Q同时从点C出发以2个单位/秒的速度沿运动,过点P作,交于E,连接,当点Q与B重合时,两动点均停止运动,设运动时间为t秒.
(1)当时,求线段的长;
(2)当运动t秒时线段的长(用含t的式子表示);
(3)运动过程中是否存在某一时刻,使与相似?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
2.如图,在中,,,,点从点开始向点以的速度移动,点从点开始沿边向点以的速度移动,当、两点中有一点到达终点时,则同时停止运动.
(1)如果、分别从、同时出发,那么经过几秒时,的面积等于?
(2)如果、分别从、同时出发,那么经过几秒时,的长度等于?
(3)几秒钟后,与相似?
3.如图,的两条直角边,,点D沿从A向B运动,速度是/秒,同时,点E沿从B向C运动,速度为/秒.动点E到达点C时运动终止.连接、、.
(1)当动点运动时间 秒时,与相似.
(2)在运动过程中,当时,为何值?请说明理由.
4.已知矩形中,,点是对角线上一点,且.点是边中点,点从点出发,沿方向运动,速度为cm/s,点从点出发,沿方向运动,速度为cm/s,两点同时开始运动,运动的时间为.若面积记为,面积记为,面积记为.当点运动到点的正上方时,两点运动停止.
(1)如图①,点在线段(包含端点)上运动时,与的函数图像如图②所示,则的长为___________cm;
(2)如图③,点在线段上运动;
①若,求此时的值;
②若,求此时的值.
【题型11 利用相似三角形测物体的高度】
1.某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图),已知小明的眼睛离地面米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为米,小亮身高米,请根据以上数据求出城楼的高度.
2.如图,屋架跨度的一半,高度.现要在屋顶上开一个天窗,在水平位置,且.求天窗高度的长.
3.用手举一根标尺,让标尺与地面垂直,调整人与旗杆的距离或人与标尺的距离,使标尺刚好挡住旗杆,此方法可测量旗杆的高度. 若人与标尺的水平距离,人与旗杆的水平距离,标尺的长度,根据测量结果,试求旗杆的高度.
4.某学校数学课外活动小组测量校园内一棵树的高度.采用的方法如下:如图,首先把支架放在离树适当距离的水平地面上点处,再把镜子水平放置在支架上点处,然后观测者沿着直线后退至点处,这时恰好在镜子里看到树的顶端.用皮尺分别测得,.若观测者目高为,支架的高为,求这棵树的高度.
【题型12 影子部分不落在地面上求物体的高度】
1.如图,在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同一时刻旗杆的影长不全落在水平地面上,有一部分落在楼房的墙上,他测得落在地面上影长为米,留在墙上的影长米,则旗杆的高度( )
A.8米 B.9米 C.10米 D.10.2米
2.数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为 .
3.小明和爸爸在公园散步,此时爸爸的影子落在了身后的地面和墙上,如图1所示.其中,段为地上的影子,段为墙上的影子.小明想利用所学知识测量出爸爸的身高.他向工作人员询问得知:公园地面与墙面所用均为厚度,长度的砖块,小明数了一下,段刚好是4块地砖的长度,而段恰好为4块地砖的厚度;同一时刻,小明观察到公园门口指示牌影子的顶端刚好到达保安亭,如图2所示,其中为指示牌的影子.已知爸爸、墙面、指示牌和保安亭均与地面垂直,指示牌高,指示牌距保安亭,请你根据以上信息,帮小明求出爸爸的身高.
4.物体在太阳光线的照射下会留下“影子”,某兴趣小组在利用影子测量物体的高度时,甲同学测得一根长为1米的垂直于地面的标杆,在地面上的影长为米,请解答下列问题.
(1)如图1,乙同学测得旗杆在地面上的影长为6米,那么旗杆的高度为 米.
(2)如图2,丙同学想测量一棵树的高度,他发现树的影子落在了地上和墙上,地面上的影长为3米,墙上的影长长为1米,则树的高度为多少?
(3)如图3,丁同学想测量一根电线杆的高度,他发现电线杆的影子恰好落在地面和一斜坡上,测得地面上的影长为4米,坡面上的影长为2米,已知斜坡的坡角为,则电线杆的高度是多少?
【题型13 位似图形】
1.在下列四个三角形中,与是位似图形且为位似中心的是( )
A.① B.② C.③ D.④
2.如图,在正方形网格中,与位似,则下列说法正确的是( )
A.位似中心是点D B.位似中心是点G
C.位似比为 D.位似比为
3.如图,已知ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD=AO,OE=BO,OF=CO,得DEF.下列说法中,错误的是( )
A.DEF与ABC是位似三角形 B.OAC与ODF是位似三角形
C.DEF与ABC周长的比是1:3 D.图中位似的两个三角形面积比是1:9
4.如图,已知的面积为24,以B为位似中心,作的位似图形,位似图形与原图形的位似比为,连接AG、DG.则的面积为 .
【题型14 位似变换作图与计算】
1.如图,在正方形网格图中,每个小正方形边长均为1,点和的顶点均为小正方形的顶点.
(1)以为位似中心,在网格图中作,使和位似,且位似比为.
(2)证明和相似.
2.如图,的顶点都在网格点上,点A的坐标为.
(1)以点O为位似中心,把按放大,在y轴的左侧,画出放大后的;
(2)点A的对应点D的坐标是______;
(3) ______.
3.在如图所示的正方形网格中,建立平面直角坐标系,的三个顶点的坐标分别为,,.
(1)画出关于原点对称的,并分别写出的坐标;
(2)在网格内,画出以点为位似中心,把放大为原来的倍后的;
(3)若也是的位似图形,点是位似中心,在图中画出点.
4.已知在平面直角坐标系中的位置如图所示:
(1)在图中画出沿x轴翻折后的;
(2)以点为位似中心,作出按放大后的位似图形;
(3)点的坐标___________;与的周长比是___________,与的面积比是___________.
参考答案
【题型1 成比例线段的计算】
1.(1)解:,
设,,
,
,
,
,,
线段的长为18,线段的长为12.
(2)解:线段是线段、的比例中项,,,
,
由题意知,,
,
线段的长为.
2.10
【分析】先设这个图距是,根据图上距离比上实际距离等于比例尺,可得关于的方程,即可求解.
【详解】设这个图距是,
则4:20000000=x:50000000,
解得x=10.
故填:10.
3.
【分析】本题主要考查了比例线段,熟练掌握比例线段的性质是解题的关键.根据比例线段的定义得到,即可得到答案.
【详解】解:由于线段,,,是成比例线段,
故,
即
解得
故答案为:.
4.(1)解:∵,,
∴,
故答案为:;
(2)解:矩形为黄金矩形,理由是:
由(1)知,
∴,
∴,
故矩形为黄金矩形;
(3)解:连接,,过D作于点G
∵,,
∴,
在中, ,
即,
则,
解得,
∴点D到线段的距离为.
【题型2 比例性质的应用】
1.C
【分析】本题考查了比例的性质,熟悉等比性质是解题的关键.分两种情况进行讨论:①当时,根据等比性质计算得出结果;②当时,则,代入计算得出结果.
【详解】解:分两种情况:
①当时,得;
②当时,
则,;
综上所述,k的值为1或.
故选:C.
2.D
【分析】本题主要考查比例性质的变形,根据比例的性质,对所给选项进行整理,找到不一定成立的选项即可
【详解】解:A.∵,∴,正确,不符合题意;
B. ∵,∴,∴,正确,不符合题意;
C. ∵,∴,∴,∴,∴,正确,不符合题意;
D.当时,原式不成立,故选项D符合题意,
故选:D
3.或
【分析】根据题意得出,三式相加得出,然后分类讨论,即可求解.
【详解】解:∵,
∴
∴
即,
当时,,
当时,,
故答案为:或.
4.25
【分析】设,得到关于k的等式,利用配方法和非负数的性质即可求解.
【详解】解:设,
∴a-1=2k,b+1=3k,c-2=4k,即a=2k+1,b=3k-1,c=4k+2,
∴a2+b2 c2= (2k+1)2+(3k-1)2 (4k+2)2
=4k2+4k+1+9k2-6k+1-(16k2+16k+4)
=4k2+4k+1+9k2-6k+1-16k2-16k-4
=-3k2-18k-2
=-3(k2+6k+9-9)-2
=-3(k+3) 2+25
∵(k+3) 2≥0,则-3(k+3) 2≤0,
∴a2+b2 c2的最大值为25,
故答案为:25.
【题型3 平行线分线段成比例的应用】
1.
【分析】根据平行线分线段成比例定理得出比例式,解答即可.
【详解】解:直线,
,
,
故答案为:.
2.C
【分析】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.
过点作平行横线的垂线,交点所在的平行横线于,交点所在的平行横线于,根据平行线分线段 成比例定理列出比例式,计算即可.
【详解】解:过点作平行横线的垂线,交点所在的平行横 线于,交点所在的平行横线于,
∵五线谱是由等距离、等长度的五条平行横线组成的,
∴,
∴,
解得:,
故选:C.
3.
【分析】先过E作,交于G,再作交于H,由平行线分线段成比例定理的推论,再结合已知条件,可分别求出和的值,相加即可.
【详解】解:作交于,作交于,如图所示:
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故答案为:.
4.或3
【分析】分点在线段的延长线和反向延长线上,两种情况进行讨论求解即可,当点在线段的延长线上时,推出为等腰三角形,三角形外角的性质求出,根据等边对等角,推出为含30 度角的直角三角形,求出的长,进而求出的长即可,当点在线段的反向延长线上时,过点作,过点作,得到,根据等边三角形和等腰三角形的性质,结合平行线分线段成比例进行求解即可.
【详解】解:当点在的延长上时,如图,
∵边长为1的等边三角形,
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴;
当点在的反向延长上时,如图,
过点作,过点作,
则:,
∵为等边三角形,,
∴,
∵,
∴,
∴,
∴,
∴;
综上:或;
故答案为:或3.
【题型4 相似三角形的判定】
1.证明:在中,,
∴,
∵,
∴,
∵,,
∴,
∴.
2.A
【分析】本题考查相似三角形的判定、相似多边形的判定,根据题意得,,,,可得,,即可证得;再根据题意得,,可得,可知新矩形与原矩形不相似,即可求解.
【详解】解:甲:根据题意得,,,,
∴,,
∴,
∴甲说法正确;
乙:根据题意得,,,则,,
∴,,
∴,
∴新矩形与原矩形不相似,
∴乙说法不正确;
故选:A.
3.(答案不唯一)
【分析】本题考查了相似三角形的判定,根据相似三角形的判定推理即可;熟练掌握相似三角形的判定是解题的关键.
【详解】解:由可得,
根据相似三角形的判定,可添加一个角或的两边对应成比例;
故可以添加:或或;
故答案为:(答案不唯一)
4.D
【分析】本题考查了相似三角形的判定、旋转的性质等知识,根据旋转的性质得到,,,,,再根据相似三角形的判定定理判断求解即可.
【详解】解:根据旋转的性质得,,
∴,
∴,,
∴,故A不符合题意;
∵,
∴,
∴,
又∵,
∴,故B不符合题意;
又,,
∴,故C不符合题意;
根据题意,无法求解与相似,
故D符合题意;
故选:D.
【题型5 利用相似三角形的性质求值】
1.C
【分析】本题主要考查了对相似三角形性质的理解,解题的关键是掌握相似三角形面积比与相似比之间的关系,即相似三角形面积比等于相似比的平方.
已知两相似三角形的相似比,即可求出面积比.根据面积差为30,可求出两三角形的面积,进而可求出面积和.
【详解】解:∵两三角形的相似比为,
∴它们的面积比为,
设较小三角形的面积为,则较大三角形的面积为,
则,
解得,
∴面积和为,
故选C.
2.D
【分析】本题考查了相似三角形的性质,根据相似三角形的性质得出,逐项分析判断,即可求解.
【详解】解:∵
∴
∴,故A,B,C正确,D错误
故选:D.
3.
【分析】本题主要考查了相似三角形的性质,解分式方程等知识点,熟练掌握相似三角形的性质是解题的关键.
三角形相似,对应边成比例,据此即可求出答案.
【详解】解:,
,
,,,
,
解得:,
经检验,是原分式方程的根,
故答案为:.
4.12
【分析】本题考查相似三角形的性质,关键是设出与它相似的三角形的三边,利用最长边构造方程.
根据相似三角形的性质,依题意设这个三角形三边为,确定,即可得出最短边长.
【详解】解:∵三角形三边之比为4:4:7,
∴与他相似的三角形的三边之比也为4:4:7,
设这个三角形三边为,
∵与它相似的三角形的最长边为,
∴,
则,
最短边长为,
故答案为:12.
【题型6 与相似多边形有关的计算】
1.B
【分析】根据对折表示出小长方形的长和宽,再根据相似多边形的判定,对应边成比例列式计算即可.
【详解】解:对折两次后的小长方形的长为b,宽为,
要使小长方形与原长方形相似,只要满足即可,
∴.
故选:B.
2.
【分析】连接,根据菱形对角线互相垂直,构建直角三角形,再根据相似,得出,再根据直角三角形30°角所对的边是斜边的一半得出,最后根据勾股定理求解即可.
【详解】解:连接,
∵四边形为菱形,,
∴,,
∴,
∵菱形与菱形相似,
∴,
∴,
∴,
根据勾股定理可得:,
即,解得:.
故答案为:.
3.D
【分析】根据勾股定理求出四边形ABCD的四条边之比,根据相似多边形的判定方法判断即可.
【详解】作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
4.(1)设矩形地砖的长为a cm,宽为b cm,
由题图可知4b=60,即b=15.
因为 所以
所以矩形地砖的长为45 cm,宽为15 cm.
(2)不相似.理由:因为所铺成矩形地面的长为 (cm),宽为60 cm,
所以大矩形的长与宽之比为:
而小矩形的长与宽之比为:
即所铺成的矩形地面的长与宽和地砖的长与宽不成比例.
所以它们不相似.
【题型7 网格中相似三角形的相关计算】
1.(1)解:如图中,点中任取两个即为所求;
(2)解:如图中,点E即为所求;
由图可知,,
,
又,
,
是直角三角形,
∴,
又∵,
∴;
(3)解:如图,取格点,连接,交于点,点P,点Q即为所求,
如图:,
四边形是平行四边形,
,
则:,
∴,
相似比为:.
2.(1)解:由图得,
,,
,
,
故答案:;
(2)解:①如图,
点为所求;
②如图,
点为所求.
3.(1)解:如图所示,即为所求.
理由:∵,,
∴,
又∵,
∴;
(2)解:如图所示,即为所求.
4.(1)解:根据题意,作图如下:
,
,
,
,
,
故取格点,格点,连接,
,
,
相似比为:,
即为所求,
故答案为:;
(2)根据题意得:
,且相似比为,作图如下:
,
取格点,格点,连接,交于点,则,
即为所求,
由(1)得,
又相似比为,
,
,
故答案为:.
(3)根据题意得,
且相似比为,
,
,
,
取格点,格点,连接,交于点,则,
即为所求,
,
又,
,
故答案为:.
【题型8 相似三角形的判定与性质的综合应用】
1.B
【分析】本题主要考查了正方形的性质,勾股定理,相似三角形的性质与判定,由正方形的性质得到,,则由勾股定理得到,求出,则,再证明,得到,即,即可得到.
【详解】解:如图所示,连接
∵四边形是正方形,
∴,,
∴,
∵,
∴,
∴,
∴
∵,
∴,
又∵,
∴,
∴,即,
∴,
故选:B.
2.(1)①证明:如图1,
∵,
∴,
∵,
∴
∵是斜边上的中线,
∴,
∴,
∴,
∴,
∴,
∵,
∴,即,
∴,
∴;
②解:如图2, 若,
在中,,
∴,
过点D作于点H,设,则,在中,,
∴,
∴,
;
(2)解:如图3,当点E在上时,
设则设
,
把代入中,得:
,
解得:, (舍去) ,
如图4, 当点E在上时,
,
∴四边形是矩形,
设
∵
∴
∵,
∴,
在中,由勾股定理得
在中, 由勾股定理得
∴解得:,(舍去)
,
综上所述,的长为:或 .
3.
【分析】本题主要考查相似三角形的判定和性质,全等三角形的判定和性质,证明是解题的关键.
先证明,可得,进而得到,从而证得,可得,进而即可求解.
【详解】解:∵,
∴,
∵,,
∴,
∴
∵,,
∴,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴设,,
∵H是的中点,
∴,
∴,
∵,
∴,
∴,
∵,
∴=.
故答案是:.
4.(1)∵四边形是正方形,
∴,,
∴,.
又∵,
∴,
∴;
(2)当P是的中点时,.
∵,
∴,即,
∴;
(3)分两种情况:
①当,且时,则有,
∴四边形为矩形,
∴,即.
②当,且时.
∵,
∴,
∴.
∵,
∴点F为的中点.
∵,
∴
,即,
∴,
∴,即;
∴满足条件的x的值为2或5;
(4).理由如下:
如图,∵四边形是正方形,
∴,,
∴.
∵E是的中点,
∴,
∴.
∵,
∴,,
∴,
∴,
∴,即,
∴,
∴
,
∴.
又∵,
∴,
∴.
【题型9 与判定相似三角形中等积式的证明】
1.(1)证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴四边形是等腰梯形;
(2)证明:∵,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
∴,
∴,
∴.
2.(1)证明:四边形是平行四边形
,
,
.
,即.
(2)①解:
,即
,
解得:(舍去负值)
②解:
,
3.(1)证明:四边形是矩形,
,
,
,
,
,
,
,
,
;
(2)证明:四边形是矩形,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
故.
4.(1)解:∵,,,
∴,
又∵,
∴,
同理可得:,;
(2)证明:∵,,
∴,
∴,即,
又∵,,
∴;
(3)解:连接,设直线和交于点K,
∴,
∴,
设,,则,,
∵点H,I,J分别为,,中点,
∴,,,
∴,,即,
∴,
∴,,
∴,
∴,
∴.
【题型10 相似三角形中的运动问题】
1.(1)当时,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴,
∵,
∴,
∴;
(2)由运动知,,
∵,
∴,
∴,
∴,
由运动知,,
∴,
在中,,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∴;
(3)∵,
∴,
若,,
∴,
∵,
∴,
∴(不合题意舍去),
若,,
∴,
∴,
∴.
故当时,与相似.
2.(1)解:设经过秒以后,面积为()
此时,,,
由,得,
整理得:,
解得:,(舍).
(2)解:设经过秒后,的长度等于,
由,得,
解得:(舍去),.
答:2秒后,的长度为.
(3)解:当时,
即,解得
当时,
,
即,
解得,
或.
3.(1)解:设经过运动时间为t秒时,与相似.
则,,, ;
1)当,即时,
;
,即,
.
2)当,即时,
,
,即,
.
和都符合,
当动点运动秒或秒时,与相似.
故答案为:或.
(2)如图,过点E作于F,
设经过运动时间为t秒时,,
则,,, ;
,即,
,,
,
,
,
,
,
,
,
,
,
,即,
(秒).
4.(1)解:由图②可知,
当x的值为时,点运动到了点,
∴,
故 (cm)
(2)解:①如图3,过点作于点
∵,
∴,
∵,
∴
在Rt中,
∴
解得:
∵点在线段上运动,
∴,
∴此时的值为3秒.
②如图3,过点作,交于点, 交于点
由题意得:,
∴,
∵,
∴,
∴,解得,
同理,
可得,
∵
∴,
∵
∴,
∴
解得:
∵,
∴此时的值为秒.
【题型11 利用相似三角形测物体的高度】
1.解:如图,过点作于点,交于点,
依题意,,
∴,
∵,
∴,
∴,
即,
解得:,
∵,
∴城楼的高度为米
2.解:由题意得,
,
又,
,
,
,
天窗高度的长.
3.解:由题意可知,
∴,,
∴,,
∴,
∵,,,则,
∴,
即:旗杆的高度为.
4.解:过点作水平线交于点,交于点,由是水平线,都是铅垂线,则四边形是矩形,四边形是矩形,如图,
,,,
,
又根据题意,得, ,
,
,即 ,
解得:,
,
答:这棵树的高度为.
【题型12 影子部分不落在地面上求物体的高度】
1.A
【分析】本题考查了相似三角形的应用,作于点,如图,则四边形为矩形,,,利用“在同一时刻物高与影长的比相等得到” ,求出从而可得到的长.
【详解】作于点,如图,
则四边形为矩形,,,
根据题意得,
即,
解得,
所以.
答:旗杆的高度为米.
故选:A.
2.4米
【分析】根据同一时刻物高与影长成正比例列式计算即可.
【详解】如图,设树高为AB,过点C作CD⊥AB于D,则CD=1.1+1.6=2.7米,DB=1米,
∵同一时刻物高与影长成正比例,
∴,
解得:AD=3,
∴AB=AD+DB=3+1=4(米).
故答案为:4米.
3.解:如图:过点作,垂足为,
由题意得:,,
指示牌高,指示牌距保安亭,
,
,
,
爸爸的身高为.
4.(1)解:∵一根长为1米的垂直于地面的标杆,在地面上的影长为米,
∴旗杆在地面上的影长为6米,旗杆的高度为12米,
故答案为:12;
(2)解:如图2,连接并延长,交直线于点H,
米,
米,
米,则,
解得:,
答:树的高度为7米;
(3)解:如图3,连接并延长,交直线于点C,过点K作于点N,
在中,米,,
则米,米,
由题意得:米,
米,
则,
解得:米,
答:电线杆的高度是米.
【题型13 位似图形】
1.B
【分析】根据位似图形的概念判断即可.
【详解】解:∵②与△ABC相似,对应点的连线相交于点O,对应边互相平行,
∴②与△ABC是位似图形且O为位似中心,
故选:B.
2.C
【分析】本题考查正方形的性质、位似图形,如果两个图形不仅是相似图形,而且对应顶点的连线所在直线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.掌握位似图形的意义与位似比求法是解题的关键.连接、、,可知位似中心在点,之间,根据两个三角形网格数可知相似比,即可得出结论.
【详解】解:如图,连接、、,
在正方形网格中,与位似,点是的中点,
位似中心在点,之间,,故选项A,B错误,
相似比为,
位似比为,故选项正确,D错误,
故选:.
3.D
【分析】根据位似三角形的定义及性质即可判断.
【详解】A、由题意知,△DEF与△ABC是位似三角形,故正确;
B、由题意知,△OAC与△ODF是位似三角形,故正确;
C、由于△DEF与△ABC是位似三角形,因而也是相似三角形,且相似比为1:3,从而周长的比也为1:3,故正确;
D、此选项没有指明是哪两个位似三角形,故错误.
故选:D.
4.4
【分析】延长EG交CD于点H,由题意可得四边形AEHD是平行四边形,则可得此平行四边形的面积为8,从而可得△ADG的面积.
【详解】延长EG交CD于点H,如图,
∵四边形ABCD是平行四边形,四边形EBFG是平行四边形,
∴AB∥CD,AD∥BC;BF∥EG,
∴AD∥EG,
∴四边形AEHD是平行四边形,
∴.
∵位似图形与原图形的位似比为,
∴,
即,
∴,
∴.
故答案为:4.
【题型14 位似变换作图与计算】
1.(1)解:如图所示:即为所求,
;
(2)证明:小正方形边长为1,
,,,,,,
,,,
∴,
∴.
2.(1)解:位似中心为点,位似比,已知,,,
∴对应点的坐标分别是,,,
连接点,如图所示,
;
(2)由(1)知,
故答案为:;
(3)如图,连接,,
,
,
,
∴,
∴设,则,
∴,
故答案为:.
3.(1)如图,,,关于原点对称,,,连接,
∴即为所求;
(2)如图,延长,,然后连接,
∴即为所求;
(3)如图,连接,相交于点,
∴点即为所求.
4.(1)解:如图,为所作;
(2)解:如图,为所作;
(3)解:点的坐标为,
∵沿x轴翻折后的,
∴,
∵按放大后的位似图形,
∴与的相似比为,
∴与的相似比为,
∴与的周长的比为,与的面积的比为.
故答案为:;;
