人教版九年级数学下册 第28章 锐角三角函数 复习题--解直角三角形的四大模型 (含解析)
文档属性
| 名称 | 人教版九年级数学下册 第28章 锐角三角函数 复习题--解直角三角形的四大模型 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 07:06:48 | ||
图片预览




文档简介
第28章《锐角三角函数》复习题--解直角三角形的四大模型
【模型一:背靠背型】
【模型分析】若三角形中有已知角时,则通过在三角形内作高,构造出两个直角三角形,求其中公共边是解题的关键.
【模型演变】
【模型突破】如图①,CE=DA,CD=EA,CE+BD=AB;如图②,CD=EF,CE=DF,AD+CE+BF=AB.
1.如图,小明与小华利用三角板测量教学楼前雕塑AB的高度.小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°;小华在五楼找到一点D,利用三角板测得A点的俯角为60°.已知CD为10米,则雕塑AB的高度是 .(,,结果精确到0.1米).
2.如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B, A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?(参考数据: ,,,,,)
3.在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为20m,求塑像的高度CF.(结果保留根号)
4.某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)
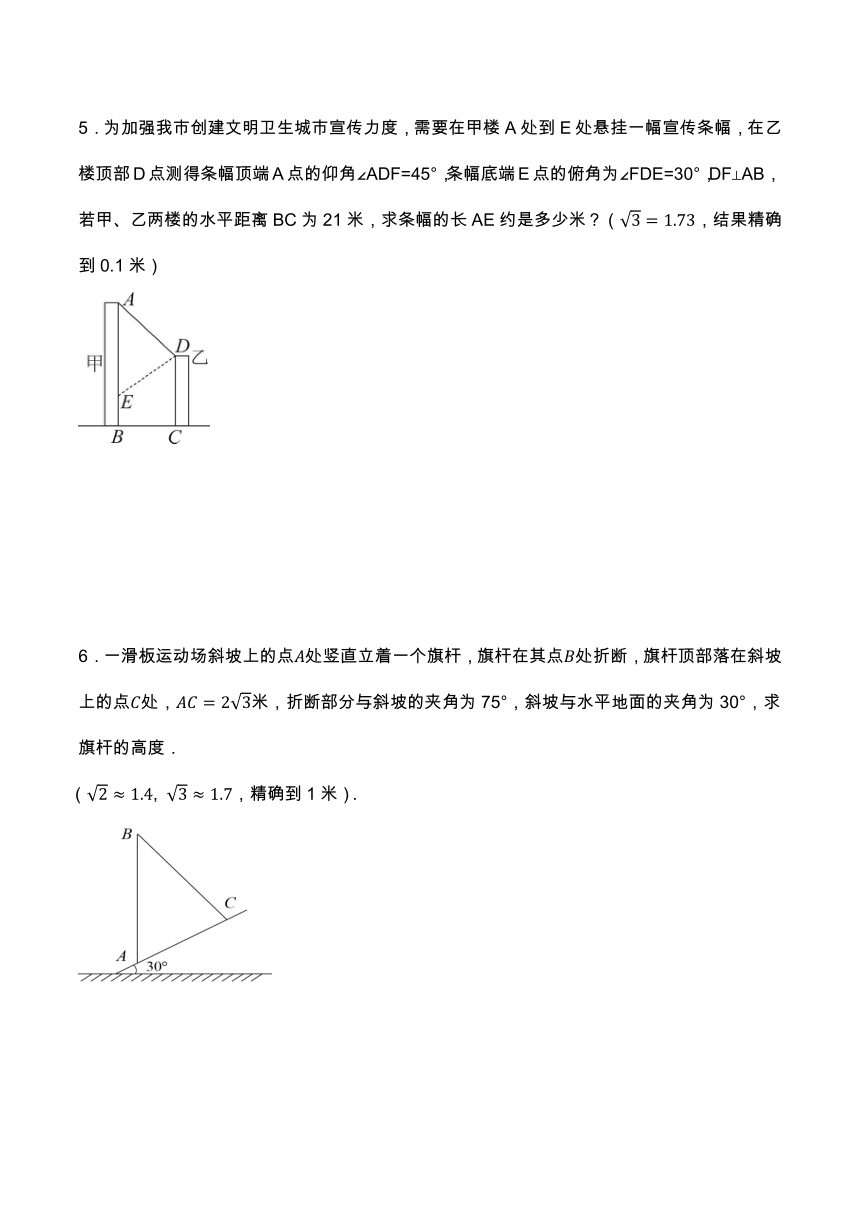
5.为加强我市创建文明卫生城市宣传力度,需要在甲楼A处到E处悬挂一幅宣传条幅,在乙楼顶部D点测得条幅顶端A点的仰角∠ADF=45°,条幅底端E点的俯角为∠FDE=30°,DF⊥AB,若甲、乙两楼的水平距离BC为21米,求条幅的长AE约是多少米?(,结果精确到0.1米)
6.一滑板运动场斜坡上的点处竖直立着一个旗杆,旗杆在其点处折断,旗杆顶部落在斜坡上的点处,米,折断部分与斜坡的夹角为75°,斜坡与水平地面的夹角为30°,求旗杆的高度.
(, ,精确到1米).
7.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔垂直于地面,在地面上选取两处分别测得和的度数(在同一条直线上).
数据收集:通过实地测量:地面上两点的距离为.
问题解决:求宝塔的高度(结果保留一位小数).
参考数据:,.
根据上述方案及数据,请你完成求解过程.
8.如图,在四边形中,,点D在上,,连接,且.
(1)求的面积.
(2)求的长度.
(本题中计算过程和结果均保留根号)
9.如图,在东西方向的海面线MN上,有A,B两艘巡逻船,两船同时收到渔船C在海面停滞点发出的求救信号,测得渔船分别在巡逻船A,B的北偏西30°和北偏东45°方向,巡逻船A和渔船C相距120海里.(结果取整数,参考数据:≈1.41,≈1.73,≈2.45)
(1)求巡逻船B与渔船C间的距离;
(2)已知在A,B两艘巡逻船间有一观测点D(A,B,D在直线MN上),测得渔船C在观测点D的北偏东15°方向,观测点D的45海里范围内有暗礁.若巡逻船B沿BC方向去营救渔船C,问有没有触礁的危险?并说明理由.
10.问题1:如图①,在四边形中,,是上一点,,.
求证:.
问题2:如图②,在四边形中,,是上一点,,.求的值.
【模型二:母子型】
【模型分析】若三角形中有已知角,通过在三角形外作高BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【模型突破】BC为公共边,如图①,AD+DC=AC;如图②,DC-BC=DB.
【模型演变1】
【模型突破】如图③,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如图④,AF=CE,AC=FE,BC+AF=BE.
【模型演变2】
【模型突破】如图⑤,BE+EC=BC;如图⑥,EC-BC=BE;如图⑦,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
【模型演变3】
【模型突破】 如图⑧,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如图⑨,BC=FG,BF=CG,EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
11.某数学学习小组利用卷尺和自制的测角仪测量魁星阁顶端距离地面的高度,如图所示,他们在地面一条水平步道上架设测角仪,先在点处测得魁星阁顶端的仰角是26°,朝魁星阁方向走20米到达处,在处测得魁星阁顶端的仰角是45°.若测角仪和的高度均为米,求魁星阁顶端距离地面的高度(图中的值).(参考数据:,,,,结果精确到米)
12.如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程.
13.如图,山坡上有一棵竖直的树AB,坡面上点D处放置高度为1.6m的测倾器CD,测倾器的顶部C与树底部B恰好在同一水平线上(即BC//MN),此时测得树顶部A的仰角为50°.已知山坡的坡度i=1∶3(即坡面上点B处的铅直高度BN与水平宽度MN的比),求树AB的高度(结果精确到0.1m.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
14.如图,某大楼的顶部竖有一块宣传牌,小明在斜坡的坡脚处测得宣传牌底部的仰角为,沿斜坡向上走到处测得宣传牌顶部的仰角为,已知斜坡的坡度,米,米,求宣传牌的高度.(测角器的高度忽略不计,参考数据:,,
15.如图,一艘渔船沿南偏东42°方向航行,在A处测得一个小岛P在其南偏东64°方向.又继续航行海里到达B处,测得小岛P位于渔船的南偏东72°方向,已知以小岛P为圆心,半径海里的圆形海域内有暗礁.如果渔船不改变航向有没有触礁的危险,请通过计算加以说明.如果有危险,渔船自B处开始,沿南偏东多少度的方向航行,能够安全通过这一海域?(参考数据:,,)
16.如图,某楼房顶部有一根天线,为了测量天线的高度,在地面上取同一条直线上的三点,,,在点处测得天线顶端的仰角为,从点走到点,测得米,从点测得天线底端的仰角为,已知,,在同一条垂直于地面的直线上,米.
(1)求与之间的距离;
(2)求天线的高度.(参考数据:,结果保留整数)
17.如图1是某商场从一楼到二楼的自动扶梯,图2是侧面示意图,MN是二楼楼顶,MN∥PQ,点C在MN上,且位于自动扶梯顶端B点的正上方,BC⊥MN.测得AB=10米,在自动扶梯底端A处测得点C的仰角为50°,点B的仰角为30°,求二楼的层高BC(结果保留根号)
(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20)
18.如图,某货船以24海里/时的速度将一批货物从处运往正东方向的处,在点处测得某岛在北偏东60°的方向上.该货船航行30分钟后到达处,此时再测得该岛在北偏东30°的方向上,
(1)求的度数;
(2)已知在岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.(参考:、)
19.如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度()
20.如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处G (点G 在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
【模型三:拥抱型】
【模型分析】分别解两个直角三角形,其中公共边BC是解题的关键.
【模型突破】BC为公共边.
【模型演变】
【模型突破】如图①,BF+FC+CE=BE;如图②,BC+CE=BE;如图③,AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
21.潮汐塔是万平口区域内的标志性建筑,在其塔顶可俯视景区全貌.某数学兴趣小组用无人机测量潮汐塔的高度,测量方案如图所示:无人机在距水平地面的点M处测得潮汐塔顶端A的俯角为,再将无人机沿水平方向飞行到达点N,测得潮汐塔底端B的俯角为(点在同一平面内),则潮汐塔的高度为( )
(结果精确到.参考数据:)
A. B. C. D.
22.如图,甲船从A处向正北方向的C岛航行,同时,乙船在C岛正东方向80海里的D处向正东方向航行,此时甲船观察到乙船在北偏东45°方向,甲船正北方向航行30海里后在B处观察到乙船在北偏东70°方向的E处,则乙船向正东方向航行了 海里.(精确到1海里,参考数据:,,)
23.如图,某幢大楼顶部有广告牌,小宇目高为米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为;接着他向大楼前进15米、站在点B处,测得广告牌顶端点的仰角为(取,计算结果保留一位小数)
(1)求这幢大楼的高;
(2)求这块广告牌的高度.
24.某数学兴趣小组学过锐角三角函数后,到市龙源湖公园测量塑像“夸父追日”的高度,如图所示,在A处测得塑像顶部D的仰角为45°,塑像底部E的仰角为30.1°,再沿AC方向前进10m到达B处,测得塑像顶部D的仰角为59.1°.求塑像“夸父追日”DE高度.(结果精确到0.1m.参考数据:sin30.1°≈0.50,cos30.1°≈0.87,tan30.1°≈0.58,sin59.1°≈0.86,cos59.1°≈0.51,tan59.1°≈1.67)
25.某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为米的发射塔,如图所示,在山脚平地上的处测得塔底的仰角为,向小山前进米到达点处,测得塔顶的仰角为,求小山的高度.
26.慈氏塔(如图①)作为湖南现存最早的砖塔之一,以其巍然 立,雄视洞庭湖,成为“巴陵胜状”之一.某兴趣小组决定利用所学知识开展以“测量慈氏塔的高度”为主题的活动,并写出如下项目报告:
课题 测量慈氏塔的高度
测量工具 测角仪、无人机等
测量示意图
测量过程 如图②,测量小组使无人机在点处以的速度竖直上升后,飞行至点处,在点处测得塔顶的俯角为,然后沿水平方向向左飞行至点处,在点处测得塔顶和点的俯角均为
说明 点均在同一竖直平面内,且点在同一水平线上,.结果精确到.参考数据:
(1)求无人机从点到点处的飞行距离;
(2)求慈氏塔的高度.
27.如图,四边形是某公园的游览步道(步道可以骑行),把四个景点连接起来,为了方便,在景点的正东方设置了休息区,其中休息区在景点的南偏西方向米处,景点在景点的北偏东方向,景点和休息区两地相距米,景点分别在休息区、景点的正东方向和正南方向.(参考数据:)
(1)求步道的长度;
(2)周末小明和小宏相约一起去公园游玩,他们在景点一起向正东出发,不久到达休息区,他们发现有两条路线到达景点,于是小宏想比赛看谁先到达景点.他们分别租了一辆共享单车,两人同时在点出发,小明选择①路线,速度为每分钟米;小宏选择②路线,速度为每分钟米,其中两人在各个景点停留的时间不计.请你通过计算说明,小明和小宏谁先到达景点呢?
28.赤水河畔的“美酒河”三个大字,是世界上最大的摩崖石刻汉字.小茜想测量绝壁上“美”字的高度,根据平面镜反射原理可推出入射光线与镜面的夹角等于反射光线与镜面的夹角(如图中,),具体操作如下:将平面镜水平放置于处,小茜站在处观测,俯角时,恰好通过平面镜看到“美”字顶端处(为小茜眼睛到地面的高度),再将平面镜水平放置于处观测,俯角时,恰好通过平面镜看到“美”字底端处.测得,,点,,,在同一水平线上,点,,在同一铅垂线上.(参考数据:,,)
(1)的高度为__________,的长为__________;
(2)求“美”字的高度.
29.风能是一种清洁无公害的可再生能源,利用风力发电非常环保.如图1所示,是一种风力发电装置;如图2为简化图,塔座建在山坡上(坡比,垂直于水平地面,,,三点共线),坡面长,三个相同长度的风轮叶片,,可绕点转动,每两个叶片之间的夹角为;当叶片静止,与重合时,在坡底F处向前走米至点处,测得点处的仰角为,又向前走米至点处,测得点处的仰角为(点,,,在同一水平线上).
(1)求叶片的长;
(2)在图2状态下,当叶片绕点顺时针转动时(如图3),求叶片顶端离水平地面的距离.(参考数据:,,,,结果保留整数)
30.图1是地下停车场的入口,图2是安装雨棚左侧支架的示意图,支架的立柱与水平线垂直,支点A在线段上,斜杆与的夹角,拉杆于点D,拉杆与的夹角.
(1)求拉杆的长;
(2)若要求停车场入口水平地面到顶部雨棚的高度不超过3.6米,问安装的雨棚高度是否符合要求?(参考数据:)
【模型四:单一型】
【模型分析】图形中只有一个直角三角形,直接利用三角函数的定义,就能求出除已知条件外的边、角.
31.如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部垂直于墙面,且当导风板所在的直线与竖直直线的夹角α为时,空调风刚好吹到床的外边沿E处,于点D,于点F.若,,床铺,求空调机的底部位置距离床的高度.(结果精确到,参考数据:,,)
32.如图1,明代科学家徐光启所著的《农政全书》中记载了中国古代的一种采桑工具—桑梯,其简单示意图如图2,已知 ,,与的夹角 为α.为保证安全,农夫将桑梯放置在水平地面上,将夹角α调整为,并用铁链锁定B、C两点、此时农夫站在离顶端D处的E处时可以高效且安全地采桑.求此时农夫所在的E处到地面的高度.(结果精确到,参考数据: )
33.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂是可伸缩的,且起重臂可绕点A在一定范围内转动,张角为,转动点A距离地面的高度为.某日,一居民家突发险情,该居民家距离地面的高度为,通过计算说明该消防车能否实施有效救援?(参考数据:,)
34.为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高为,,支架为,面板长为,为.(厚度忽略不计)
(1)求支点C离桌面l的高度:(计算结果保留根号)
(2)小吉通过查阅资料,当面板绕点转动时,面板与桌面的夹角满足时,能保护视力.当从变化到的过程中,问面板上端离桌面的高度是增加了还是减少了?增加或减少了多少?(精确到,参考数据:,,)
35.如图1是可调节高度和桌面角度的电脑桌,它的左视图可以抽象成如图2所示的图形,底座长为,支架垂直平分,桌面的中点固定在支架处,宽为.身高为的使用者站立处点与点,在同一条直线上,.点到点的距离是视线距离.
(1)如图,当,时,求视线距离的长;
(2)如图,使用者坐下时,高度下降,当桌面与的夹角为时,恰有视线,问需要将支架调整到多少?(参考数据:,,)
36.森林防火不仅是政府和相关部门的责任,每个公民应当参与到森林防火工作中,了解相关防火知识并在日常生活中做出相应的贡献.如图所示,在一条笔直公路上,公路两旁是林地,位于森林防火卡点的北偏东方向的处发生火灾,防火员从卡点去火灾处救援有两种方案,方案1:防火员立即骑车沿正东方向行驶800米到达离点最近的处再跑步到点救援;方案2:防火员从卡点直接跑步前往处救援.若防火员的跑步速度为,骑车的速度为.(参考数据:,,,,,)
(1)的长为__________米(结果保留整数);
(2)防火员必须在两个方案中选择一个,请问选择哪个方案更合理,请通过计算说明理由.
37.“彼此让一让,路宽心更宽”,斑马线前礼让行人是城市文明的一种具体体现,也是司机理应履行的一项法定义务,我市设立了“礼让行人”交通标识.某数学小组在老师的指导下对某路口的交通情况进行了如下探究.
【问题情景】
如图,某无红绿灯的路口有一行人从点A处出发,通过斑马线时,正好有一辆位于车道中间的小汽车从点B(小汽车前沿中点)沿该车道中间直线匀速朝斑马线驶去,此时.已知行人的速度是,每个车道宽,双向车道中间有宽的隔离带.
【问题解决】
(1) ;
(2)若在B点时小汽车司机发现行人后,立即减速慢行,结果在行人到达点C时,小汽车前沿离行人还有,此时司机停车“礼让行人”,求小汽车从点B开始减速到停下这一段的行驶的距离.(参考数据:)
38.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,假设亮亮与无人机在同一平面内,则无人机距离地面的高度约为多少米.(结果精确到米,参考数据:,)
39.某县消防大队到某小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点在一定范围内转动,张角为转动点距离地面的高度为.当起重臂长度为,张角,求云梯消防车最高点距离地面的高度.(参考数据:,,,)
40.图①是小明家在利用车载云梯搬运装修垃圾,将其抽象成如图②所示的示意图,已知.,垂足分别为,测得.求云梯顶端A到地面的距离的长.(结果取整数.参考数据:)
参考答案
【模型一:背靠背型】
1.6.8米
【分析】利用题目中的仰俯角将其转化为题目直角三角形的内角,分别在Rt△ACE中和Rt△BCE中求得AC和BE的长,两者相加即为雕塑的高.
【详解】解:过点C作CE⊥AB于E.
∵∠FDA=60°,∠ACE=30°
∴∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=180°-30°-60°=90°,
∵CD=10,
∴AC=CD=5.
在Rt△ACE中,
∵∠AEC=90°,∠ACE=30°,
∴AE=AC=,
∵cos∠ACE=,
∴CE=AC cos∠ACE=5×cos30°=,
在Rt△BCE中,
∵∠BCE=45°,
∴∠CBE=90°-∠BCE=45°,
∴∠BCE=∠CBE,
∴BE=CE=,
∴AB=AE+BE=(+)≈6.8(米).
所以,雕塑AB的高度约为6.8米,
故答案为6.8米.
2.解答:过点A作AH⊥BC,垂足为点H.
由题意,得∠ACH=67°,∠B=37°,AB=20.
在Rt△ABH中,
∵ , ,
∴ ,
,
在Rt△ACH中,
∵ ,
∴ ,
∴BC=BH+CH≈16+5=21,
∵21÷25<1,
∴巡逻艇能在1小时内到达渔船C处.
3.解:,
,
在中,
,
,
在中,
,,
,
则.
即.
.
由题意知:
答:塑像的高为.
4.过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
∵在Rt△AED中,∠ADC=37°,AD=5,
∴cos37°==≈0.8,
∴DE≈4,
∵sin37°==≈0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CE=AE·tan∠CAE=AE=,
∴AC=2CE=2,
∴AB=AC+CE+ED=2++4=3+4≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
5.解:
过点D作DF⊥AB,如图所示:
在Rt△ADF中,DF=BC=21米,∠ADF=45°
∴AF=DF=21米
在Rt△EDF中,DF=21米,∠EDF=30°
∴EF=DF×tan30°=米
∴AE=AF+BF=+21≈33.1米.
答:条幅的长AE约是33.1米.
6.解:过点作于点,
,,,,,
又,
,
,,,
答:旗杆的高度约为9米.
7.解: 设,
在中,,
在中,,
,
解得,.
答:宝塔的高度约为.
8.解:(1)过点A作,交于点F,
由题意得.
设.
∵,
∴.
在中,∵,
∴,
∴,
∴.
∴
∴
.
(2)过点B作,交于点G,
∵BC⊥CE,AF⊥CE,BG⊥AF,
∴四边形BCFG为矩形,.
∵
∵,
∴.
∴.
9.解:(1)作于,如图1所示:
则,,,,
,,是等腰直角三角形,
,,
答:巡逻船与渔船间的距离为海里;
(2)没有触礁的危险;理由如下:
由题意得:,
,
,
,
,
,即,
解得:,
(海里);
作于,如图2所示:
,
是等腰直角三角形,
(海里),
,
没有触礁的危险.
10.问题1:证明:∵,
∴.
∵,
∴.
∴.
在和中,
,
∴.
∴,,
∴.
问题2:如图,分别过点、作的垂线,垂足为、.
由(1)可知,
在和中,,
∴,,
,.
∴,.
∴.
【模型二:母子型】
11.
解:由题意知,米,米,设米,在中,
米,,
米,
米,
在中,
,
,
即0.49×(20+)≈ ,
解得米,
米,
故魁星阁顶端距离地面的高度约为米.
12解:由题意得:AB=260m,AF=BG=CE=1.6m,DE⊥AC,
,
,
,
,
在中,,
,
即塔的高度DE为.
13.解:∵山坡BM的坡度i=1∶3,
∴i=1∶3=tanM,
∵BC//MN,
∴∠CBD=∠M,
∴tan∠CBD==tanM=1∶3,
∴BC=3CD=4.8(m),
在Rt△ABC中,tan∠ACB==tan50°≈1.19,
∴AB≈1.19BC=1.19×4.8≈5.7(m),
即树AB的高度约为5.7m.
14.解:过分别作、的垂线,设垂足为、,
则,,
在中,
斜坡的坡度,米,
设米,米,
,
,
米,米,
在中,,
米,
(米),
在中,(米),
(米).
答:宣传牌的高度为2米.
15.解:如图,过点P作PC垂直于AB所在直线,垂足为C,
根据题意可得,,
在中,,
在中,,
∴,
解得,
∵,
∴如果渔船不改变航向有触礁的危险,
∵,
∴若改变航向,刚好到暗礁区域边界时的,
此时,
即如果有危险,渔船自B处开始,沿南偏东小于45度的方向航行,能够安全通过这一海域.
16.(1)依题意可得,在中, ,
米,
米,米.
即之间的距离为30米.
(2)在中,,米,
(米),
米,米.
由.并精确到整数可得米.
即天线的高度约为27米.
17.解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
在Rt△ABD中,∵AB=10米,∠BAD=30°,
∴(米),(米),
在Rt△CDA中,∠CDA=90°,∠CAD=50°,
∴(米),
∴(米).
18.(1)∵,,
∴.
(2)过点作于,
由题意,,,
∴,
∴,
∴(海里),
在中,,
∴,
∵.
所以货船继续向正东方向行驶无触礁危险.
19.如图,在Rt△FGA中,
设AG=FG=x米,
在Rt△AEG中,=tan30°,
解得,x==4.05米,
∴AB=1.6+4.05=5.65米.
答:旗杆AB的高度为5.65米.
20.(1)能看到;
由题意得,∠DFG=90°-53°=37°,
则=tan∠DFG,
∵DF=4米,
∴DG=4×tan37°≈4×0.75=3(米),
故能看到这只老鼠;
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又=sin∠ACG=sin37°,
则CG==9.5(米),
答:要捕捉到这只老鼠,猫头鹰至少要飞约9.5米.
【模型三:拥抱型】
21.B
【分析】本题考査了解直角三角形的应用一仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
延长交于点C,根据题意得,然后在中,利用锐角三角函数的定义求出的长,从而求出的长,再在中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系进行计算,即可解答.
【详解】如图,延长交于点C.
由题意得.
在中,,
,
.
在中,,
,
.
故选B.
22.58
【分析】本题考查了解直角三角形的应用一方向角问题,根据题意可得:海里,然后在中,利用锐角三角函数的定义求出的长,从而求出的长,再在中,利用锐角三角函数的定义求出的长,从而求的长.
【详解】解:由题意得:(海里),
在中,海里,
∴(海里)
(海里),
在中,,
∴(海里),
(海里),
即乙船向正东方向航行了58海里,
故答案为:58
23.(1)解:在中,米;
由 ,
得米;
又因为米,
因而大楼米,
答:楼高为米;
(2)解:∵在中,米,
,
∴米;
因而广告牌米;
答:广告牌的高度为米.
24.解:在Rt△ACD中,,则.
设,则
在Rt△BCD中,.
∴
∴
解得:.
在Rt△ACE中,.
∴
答:塑像“夸父追日”DE 的高度约为10.5米.
25.解:设为米,则米,∵ ∴,而米,
在中,,
则米,米,
在中,,
解得.
答:小山的高度为米.
26.(1)解:根据题意得:,,
在中,,
;
(2)解:过点D作,交延长线于点H,
,
,
,
设,则,
在中,
,
,
解得:,
,
,
四边形是矩形,
,
,
答:慈氏塔的高度为.
27.(1)解:由题意得,,,,米,米,
∴,
过点作于,则,
∴为等腰直角三角形,
∴米,
∴米,
∴米;
(2)解:∵,,,
∴米,米,
∴路线②的路程为米,
∴小宏到达景点的时间为分钟,
∵路线①的路程为米,
∴小明到达景点的时间为分钟,
∵,
∴小宏先到达景点.
28.(1)解:,
,
,
是等腰直角三角形,
,
在中,,,
,
;
故答案为:,2;
(2),
,
,
,
由题意可知,
,
,
在中,
,
,
即“美”字的高度约为.
29.(1)解:∵垂直于水平地面,
∴,
∵坡比,
∴,
设,则,
∵坡面长,
∴,
解得:,(负值舍去)
∴,,
∵,
∴,
由题意得:,
∴,
∵,
∴.
由题意得:,
∴,
∴.
(2)如图,过点作于点,于,
∴,
∴四边形是矩形,
∴,
∵叶片绕点顺时针转动,
∴,
∵,
∴,
由题意得:,
∴,
∴.
∴叶片顶端离水平地面的距离为.
30.(1)解:在中,,,
,
,
,
,
,
在中,,
,
该支架的边的长为;
(2)解:符合要求,过程如下:
过点作,垂足为,
∵,
∴四边形是矩形
则,,
在中,,,
,
,
,
,
,
,
在中,,
,
安装雨棚的高度是合格的.
【模型四:单一型】
31.解:由题知 , 四边形 是矩形,,,
∴.
在 中 ,
∴
∴ .
答:空调机的底部位置距离床的高度约为.
32.解:如图所示,过点作于H,
∵米,,米,米,
∴,米,米,
∴,
在中,米;
答:农夫所在的E处到地面的高度为米.
33.解:当,时,过点C作于F,过点A作于点M,则四边形是矩形,
∴,,
∵,
∴,
在中,,
∴,
∴,
∵,
∴该消防车能实施有效救援.
34.(1)解:过点作于点,过点作于点,
.
由题意得:,
四边形为矩形,
,.
,
.
,
.
.
答:支点离桌面的高度为;
(2)解:过点作,过点作于点,
.
,,
.
当时,;
当时,;
当从变化到的过程中,面板上端离桌面的高度是增加了,增加了约.
35.(1)解:如图,连接,延长交于点,
根据题意可得四边形是矩形,
∴,
∵,,
∴,,
∴,,
∴,
在中,由勾股定理得:,
∴视线距离的长为;
(2)解:如图,连接,延长交于点,
由题意可得:,,,,
在中,,即,
∴,
∴,
∴需要将支架调整到.
36.(1)解:由题意,知米,,
在中,
(米),
故答案为:976;
(2)解:选择方案一更合理.
理由:在中,
(米),
方案一需要时间为:,
方案二需要时间为:,
,
选择方案一更合理.
37.(1)解:根据题意得:(米),
故答案为:8;
(2)由题意可知,,
∴,
∴(米),
∴(米),
答:小汽车从点B开始减速到停下这一段的行驶的距离为31米.
38.解:如图所示,过点A作地面的垂线,垂足为B,亮亮的位置用表示,过点D作于C,则四边形是矩形,
∴米,米,
在中,米,,
∴米,
∴米,
答:无人机距离地面的高度约为米.
39.解:过点作,垂足为,
,
四边形是矩形,
,,
,
,
在中,,
,
,
云梯消防车最高点距离地面的高度为.
40.如图,延长交于点H.
,
,
,
四边形是矩形,
,
.
在中,
,
,
答:云梯顶端A到地面的距离的长约为.
【模型一:背靠背型】
【模型分析】若三角形中有已知角时,则通过在三角形内作高,构造出两个直角三角形,求其中公共边是解题的关键.
【模型演变】
【模型突破】如图①,CE=DA,CD=EA,CE+BD=AB;如图②,CD=EF,CE=DF,AD+CE+BF=AB.
1.如图,小明与小华利用三角板测量教学楼前雕塑AB的高度.小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°;小华在五楼找到一点D,利用三角板测得A点的俯角为60°.已知CD为10米,则雕塑AB的高度是 .(,,结果精确到0.1米).
2.如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B, A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?(参考数据: ,,,,,)
3.在一次课外活动中,甲、乙两位同学测量公园中孔子塑像的高度,他们分别在A,B两处用高度为1.5m的测角仪测得塑像顶部C的仰角分别为30°,45°,两人间的水平距离AB为20m,求塑像的高度CF.(结果保留根号)
4.某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜后在C处折断倒在地上,树的顶部恰好接触到地面D处,测得∠ACD=60°,∠ADC=37°,AD=5米,求这棵大树AB的高.(结果精确到0.1米)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.73)
5.为加强我市创建文明卫生城市宣传力度,需要在甲楼A处到E处悬挂一幅宣传条幅,在乙楼顶部D点测得条幅顶端A点的仰角∠ADF=45°,条幅底端E点的俯角为∠FDE=30°,DF⊥AB,若甲、乙两楼的水平距离BC为21米,求条幅的长AE约是多少米?(,结果精确到0.1米)
6.一滑板运动场斜坡上的点处竖直立着一个旗杆,旗杆在其点处折断,旗杆顶部落在斜坡上的点处,米,折断部分与斜坡的夹角为75°,斜坡与水平地面的夹角为30°,求旗杆的高度.
(, ,精确到1米).
7.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔垂直于地面,在地面上选取两处分别测得和的度数(在同一条直线上).
数据收集:通过实地测量:地面上两点的距离为.
问题解决:求宝塔的高度(结果保留一位小数).
参考数据:,.
根据上述方案及数据,请你完成求解过程.
8.如图,在四边形中,,点D在上,,连接,且.
(1)求的面积.
(2)求的长度.
(本题中计算过程和结果均保留根号)
9.如图,在东西方向的海面线MN上,有A,B两艘巡逻船,两船同时收到渔船C在海面停滞点发出的求救信号,测得渔船分别在巡逻船A,B的北偏西30°和北偏东45°方向,巡逻船A和渔船C相距120海里.(结果取整数,参考数据:≈1.41,≈1.73,≈2.45)
(1)求巡逻船B与渔船C间的距离;
(2)已知在A,B两艘巡逻船间有一观测点D(A,B,D在直线MN上),测得渔船C在观测点D的北偏东15°方向,观测点D的45海里范围内有暗礁.若巡逻船B沿BC方向去营救渔船C,问有没有触礁的危险?并说明理由.
10.问题1:如图①,在四边形中,,是上一点,,.
求证:.
问题2:如图②,在四边形中,,是上一点,,.求的值.
【模型二:母子型】
【模型分析】若三角形中有已知角,通过在三角形外作高BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键.
【模型突破】BC为公共边,如图①,AD+DC=AC;如图②,DC-BC=DB.
【模型演变1】
【模型突破】如图③,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如图④,AF=CE,AC=FE,BC+AF=BE.
【模型演变2】
【模型突破】如图⑤,BE+EC=BC;如图⑥,EC-BC=BE;如图⑦,AC=FG,AF=CG,AD+DC=FG,BC+AF=BG.
【模型演变3】
【模型突破】 如图⑧,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如图⑨,BC=FG,BF=CG,EF+BC=EG,BD+DF=BF,AC+BD+DF=AG.
11.某数学学习小组利用卷尺和自制的测角仪测量魁星阁顶端距离地面的高度,如图所示,他们在地面一条水平步道上架设测角仪,先在点处测得魁星阁顶端的仰角是26°,朝魁星阁方向走20米到达处,在处测得魁星阁顶端的仰角是45°.若测角仪和的高度均为米,求魁星阁顶端距离地面的高度(图中的值).(参考数据:,,,,结果精确到米)
12.如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程.
13.如图,山坡上有一棵竖直的树AB,坡面上点D处放置高度为1.6m的测倾器CD,测倾器的顶部C与树底部B恰好在同一水平线上(即BC//MN),此时测得树顶部A的仰角为50°.已知山坡的坡度i=1∶3(即坡面上点B处的铅直高度BN与水平宽度MN的比),求树AB的高度(结果精确到0.1m.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
14.如图,某大楼的顶部竖有一块宣传牌,小明在斜坡的坡脚处测得宣传牌底部的仰角为,沿斜坡向上走到处测得宣传牌顶部的仰角为,已知斜坡的坡度,米,米,求宣传牌的高度.(测角器的高度忽略不计,参考数据:,,
15.如图,一艘渔船沿南偏东42°方向航行,在A处测得一个小岛P在其南偏东64°方向.又继续航行海里到达B处,测得小岛P位于渔船的南偏东72°方向,已知以小岛P为圆心,半径海里的圆形海域内有暗礁.如果渔船不改变航向有没有触礁的危险,请通过计算加以说明.如果有危险,渔船自B处开始,沿南偏东多少度的方向航行,能够安全通过这一海域?(参考数据:,,)
16.如图,某楼房顶部有一根天线,为了测量天线的高度,在地面上取同一条直线上的三点,,,在点处测得天线顶端的仰角为,从点走到点,测得米,从点测得天线底端的仰角为,已知,,在同一条垂直于地面的直线上,米.
(1)求与之间的距离;
(2)求天线的高度.(参考数据:,结果保留整数)
17.如图1是某商场从一楼到二楼的自动扶梯,图2是侧面示意图,MN是二楼楼顶,MN∥PQ,点C在MN上,且位于自动扶梯顶端B点的正上方,BC⊥MN.测得AB=10米,在自动扶梯底端A处测得点C的仰角为50°,点B的仰角为30°,求二楼的层高BC(结果保留根号)
(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20)
18.如图,某货船以24海里/时的速度将一批货物从处运往正东方向的处,在点处测得某岛在北偏东60°的方向上.该货船航行30分钟后到达处,此时再测得该岛在北偏东30°的方向上,
(1)求的度数;
(2)已知在岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.(参考:、)
19.如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度()
20.如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处G (点G 在DE上)距D点3米.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
【模型三:拥抱型】
【模型分析】分别解两个直角三角形,其中公共边BC是解题的关键.
【模型突破】BC为公共边.
【模型演变】
【模型突破】如图①,BF+FC+CE=BE;如图②,BC+CE=BE;如图③,AB=GE,AG=BE,BC+CE=AG,DG+AB=DE.
21.潮汐塔是万平口区域内的标志性建筑,在其塔顶可俯视景区全貌.某数学兴趣小组用无人机测量潮汐塔的高度,测量方案如图所示:无人机在距水平地面的点M处测得潮汐塔顶端A的俯角为,再将无人机沿水平方向飞行到达点N,测得潮汐塔底端B的俯角为(点在同一平面内),则潮汐塔的高度为( )
(结果精确到.参考数据:)
A. B. C. D.
22.如图,甲船从A处向正北方向的C岛航行,同时,乙船在C岛正东方向80海里的D处向正东方向航行,此时甲船观察到乙船在北偏东45°方向,甲船正北方向航行30海里后在B处观察到乙船在北偏东70°方向的E处,则乙船向正东方向航行了 海里.(精确到1海里,参考数据:,,)
23.如图,某幢大楼顶部有广告牌,小宇目高为米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为;接着他向大楼前进15米、站在点B处,测得广告牌顶端点的仰角为(取,计算结果保留一位小数)
(1)求这幢大楼的高;
(2)求这块广告牌的高度.
24.某数学兴趣小组学过锐角三角函数后,到市龙源湖公园测量塑像“夸父追日”的高度,如图所示,在A处测得塑像顶部D的仰角为45°,塑像底部E的仰角为30.1°,再沿AC方向前进10m到达B处,测得塑像顶部D的仰角为59.1°.求塑像“夸父追日”DE高度.(结果精确到0.1m.参考数据:sin30.1°≈0.50,cos30.1°≈0.87,tan30.1°≈0.58,sin59.1°≈0.86,cos59.1°≈0.51,tan59.1°≈1.67)
25.某数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为米的发射塔,如图所示,在山脚平地上的处测得塔底的仰角为,向小山前进米到达点处,测得塔顶的仰角为,求小山的高度.
26.慈氏塔(如图①)作为湖南现存最早的砖塔之一,以其巍然 立,雄视洞庭湖,成为“巴陵胜状”之一.某兴趣小组决定利用所学知识开展以“测量慈氏塔的高度”为主题的活动,并写出如下项目报告:
课题 测量慈氏塔的高度
测量工具 测角仪、无人机等
测量示意图
测量过程 如图②,测量小组使无人机在点处以的速度竖直上升后,飞行至点处,在点处测得塔顶的俯角为,然后沿水平方向向左飞行至点处,在点处测得塔顶和点的俯角均为
说明 点均在同一竖直平面内,且点在同一水平线上,.结果精确到.参考数据:
(1)求无人机从点到点处的飞行距离;
(2)求慈氏塔的高度.
27.如图,四边形是某公园的游览步道(步道可以骑行),把四个景点连接起来,为了方便,在景点的正东方设置了休息区,其中休息区在景点的南偏西方向米处,景点在景点的北偏东方向,景点和休息区两地相距米,景点分别在休息区、景点的正东方向和正南方向.(参考数据:)
(1)求步道的长度;
(2)周末小明和小宏相约一起去公园游玩,他们在景点一起向正东出发,不久到达休息区,他们发现有两条路线到达景点,于是小宏想比赛看谁先到达景点.他们分别租了一辆共享单车,两人同时在点出发,小明选择①路线,速度为每分钟米;小宏选择②路线,速度为每分钟米,其中两人在各个景点停留的时间不计.请你通过计算说明,小明和小宏谁先到达景点呢?
28.赤水河畔的“美酒河”三个大字,是世界上最大的摩崖石刻汉字.小茜想测量绝壁上“美”字的高度,根据平面镜反射原理可推出入射光线与镜面的夹角等于反射光线与镜面的夹角(如图中,),具体操作如下:将平面镜水平放置于处,小茜站在处观测,俯角时,恰好通过平面镜看到“美”字顶端处(为小茜眼睛到地面的高度),再将平面镜水平放置于处观测,俯角时,恰好通过平面镜看到“美”字底端处.测得,,点,,,在同一水平线上,点,,在同一铅垂线上.(参考数据:,,)
(1)的高度为__________,的长为__________;
(2)求“美”字的高度.
29.风能是一种清洁无公害的可再生能源,利用风力发电非常环保.如图1所示,是一种风力发电装置;如图2为简化图,塔座建在山坡上(坡比,垂直于水平地面,,,三点共线),坡面长,三个相同长度的风轮叶片,,可绕点转动,每两个叶片之间的夹角为;当叶片静止,与重合时,在坡底F处向前走米至点处,测得点处的仰角为,又向前走米至点处,测得点处的仰角为(点,,,在同一水平线上).
(1)求叶片的长;
(2)在图2状态下,当叶片绕点顺时针转动时(如图3),求叶片顶端离水平地面的距离.(参考数据:,,,,结果保留整数)
30.图1是地下停车场的入口,图2是安装雨棚左侧支架的示意图,支架的立柱与水平线垂直,支点A在线段上,斜杆与的夹角,拉杆于点D,拉杆与的夹角.
(1)求拉杆的长;
(2)若要求停车场入口水平地面到顶部雨棚的高度不超过3.6米,问安装的雨棚高度是否符合要求?(参考数据:)
【模型四:单一型】
【模型分析】图形中只有一个直角三角形,直接利用三角函数的定义,就能求出除已知条件外的边、角.
31.如图1是一间安装有壁挂式空调的卧室的一部分,如图2是该空调挂机的侧面示意图.已知空调挂机底部垂直于墙面,且当导风板所在的直线与竖直直线的夹角α为时,空调风刚好吹到床的外边沿E处,于点D,于点F.若,,床铺,求空调机的底部位置距离床的高度.(结果精确到,参考数据:,,)
32.如图1,明代科学家徐光启所著的《农政全书》中记载了中国古代的一种采桑工具—桑梯,其简单示意图如图2,已知 ,,与的夹角 为α.为保证安全,农夫将桑梯放置在水平地面上,将夹角α调整为,并用铁链锁定B、C两点、此时农夫站在离顶端D处的E处时可以高效且安全地采桑.求此时农夫所在的E处到地面的高度.(结果精确到,参考数据: )
33.图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂是可伸缩的,且起重臂可绕点A在一定范围内转动,张角为,转动点A距离地面的高度为.某日,一居民家突发险情,该居民家距离地面的高度为,通过计算说明该消防车能否实施有效救援?(参考数据:,)
34.为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高为,,支架为,面板长为,为.(厚度忽略不计)
(1)求支点C离桌面l的高度:(计算结果保留根号)
(2)小吉通过查阅资料,当面板绕点转动时,面板与桌面的夹角满足时,能保护视力.当从变化到的过程中,问面板上端离桌面的高度是增加了还是减少了?增加或减少了多少?(精确到,参考数据:,,)
35.如图1是可调节高度和桌面角度的电脑桌,它的左视图可以抽象成如图2所示的图形,底座长为,支架垂直平分,桌面的中点固定在支架处,宽为.身高为的使用者站立处点与点,在同一条直线上,.点到点的距离是视线距离.
(1)如图,当,时,求视线距离的长;
(2)如图,使用者坐下时,高度下降,当桌面与的夹角为时,恰有视线,问需要将支架调整到多少?(参考数据:,,)
36.森林防火不仅是政府和相关部门的责任,每个公民应当参与到森林防火工作中,了解相关防火知识并在日常生活中做出相应的贡献.如图所示,在一条笔直公路上,公路两旁是林地,位于森林防火卡点的北偏东方向的处发生火灾,防火员从卡点去火灾处救援有两种方案,方案1:防火员立即骑车沿正东方向行驶800米到达离点最近的处再跑步到点救援;方案2:防火员从卡点直接跑步前往处救援.若防火员的跑步速度为,骑车的速度为.(参考数据:,,,,,)
(1)的长为__________米(结果保留整数);
(2)防火员必须在两个方案中选择一个,请问选择哪个方案更合理,请通过计算说明理由.
37.“彼此让一让,路宽心更宽”,斑马线前礼让行人是城市文明的一种具体体现,也是司机理应履行的一项法定义务,我市设立了“礼让行人”交通标识.某数学小组在老师的指导下对某路口的交通情况进行了如下探究.
【问题情景】
如图,某无红绿灯的路口有一行人从点A处出发,通过斑马线时,正好有一辆位于车道中间的小汽车从点B(小汽车前沿中点)沿该车道中间直线匀速朝斑马线驶去,此时.已知行人的速度是,每个车道宽,双向车道中间有宽的隔离带.
【问题解决】
(1) ;
(2)若在B点时小汽车司机发现行人后,立即减速慢行,结果在行人到达点C时,小汽车前沿离行人还有,此时司机停车“礼让行人”,求小汽车从点B开始减速到停下这一段的行驶的距离.(参考数据:)
38.为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,假设亮亮与无人机在同一平面内,则无人机距离地面的高度约为多少米.(结果精确到米,参考数据:,)
39.某县消防大队到某小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点在一定范围内转动,张角为转动点距离地面的高度为.当起重臂长度为,张角,求云梯消防车最高点距离地面的高度.(参考数据:,,,)
40.图①是小明家在利用车载云梯搬运装修垃圾,将其抽象成如图②所示的示意图,已知.,垂足分别为,测得.求云梯顶端A到地面的距离的长.(结果取整数.参考数据:)
参考答案
【模型一:背靠背型】
1.6.8米
【分析】利用题目中的仰俯角将其转化为题目直角三角形的内角,分别在Rt△ACE中和Rt△BCE中求得AC和BE的长,两者相加即为雕塑的高.
【详解】解:过点C作CE⊥AB于E.
∵∠FDA=60°,∠ACE=30°
∴∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=180°-30°-60°=90°,
∵CD=10,
∴AC=CD=5.
在Rt△ACE中,
∵∠AEC=90°,∠ACE=30°,
∴AE=AC=,
∵cos∠ACE=,
∴CE=AC cos∠ACE=5×cos30°=,
在Rt△BCE中,
∵∠BCE=45°,
∴∠CBE=90°-∠BCE=45°,
∴∠BCE=∠CBE,
∴BE=CE=,
∴AB=AE+BE=(+)≈6.8(米).
所以,雕塑AB的高度约为6.8米,
故答案为6.8米.
2.解答:过点A作AH⊥BC,垂足为点H.
由题意,得∠ACH=67°,∠B=37°,AB=20.
在Rt△ABH中,
∵ , ,
∴ ,
,
在Rt△ACH中,
∵ ,
∴ ,
∴BC=BH+CH≈16+5=21,
∵21÷25<1,
∴巡逻艇能在1小时内到达渔船C处.
3.解:,
,
在中,
,
,
在中,
,,
,
则.
即.
.
由题意知:
答:塑像的高为.
4.过点A作AE⊥CD于点E,则∠AEC=∠AED=90°.
∵在Rt△AED中,∠ADC=37°,AD=5,
∴cos37°==≈0.8,
∴DE≈4,
∵sin37°==≈0.6,
∴AE≈3,
在Rt△AEC中,
∵∠CAE=90°﹣∠ACE=90°﹣60°=30°,
∴CE=AE·tan∠CAE=AE=,
∴AC=2CE=2,
∴AB=AC+CE+ED=2++4=3+4≈9.2(米).
答:这棵大树AB原来的高度约是9.2米.
5.解:
过点D作DF⊥AB,如图所示:
在Rt△ADF中,DF=BC=21米,∠ADF=45°
∴AF=DF=21米
在Rt△EDF中,DF=21米,∠EDF=30°
∴EF=DF×tan30°=米
∴AE=AF+BF=+21≈33.1米.
答:条幅的长AE约是33.1米.
6.解:过点作于点,
,,,,,
又,
,
,,,
答:旗杆的高度约为9米.
7.解: 设,
在中,,
在中,,
,
解得,.
答:宝塔的高度约为.
8.解:(1)过点A作,交于点F,
由题意得.
设.
∵,
∴.
在中,∵,
∴,
∴,
∴.
∴
∴
.
(2)过点B作,交于点G,
∵BC⊥CE,AF⊥CE,BG⊥AF,
∴四边形BCFG为矩形,.
∵
∵,
∴.
∴.
9.解:(1)作于,如图1所示:
则,,,,
,,是等腰直角三角形,
,,
答:巡逻船与渔船间的距离为海里;
(2)没有触礁的危险;理由如下:
由题意得:,
,
,
,
,
,即,
解得:,
(海里);
作于,如图2所示:
,
是等腰直角三角形,
(海里),
,
没有触礁的危险.
10.问题1:证明:∵,
∴.
∵,
∴.
∴.
在和中,
,
∴.
∴,,
∴.
问题2:如图,分别过点、作的垂线,垂足为、.
由(1)可知,
在和中,,
∴,,
,.
∴,.
∴.
【模型二:母子型】
11.
解:由题意知,米,米,设米,在中,
米,,
米,
米,
在中,
,
,
即0.49×(20+)≈ ,
解得米,
米,
故魁星阁顶端距离地面的高度约为米.
12解:由题意得:AB=260m,AF=BG=CE=1.6m,DE⊥AC,
,
,
,
,
在中,,
,
即塔的高度DE为.
13.解:∵山坡BM的坡度i=1∶3,
∴i=1∶3=tanM,
∵BC//MN,
∴∠CBD=∠M,
∴tan∠CBD==tanM=1∶3,
∴BC=3CD=4.8(m),
在Rt△ABC中,tan∠ACB==tan50°≈1.19,
∴AB≈1.19BC=1.19×4.8≈5.7(m),
即树AB的高度约为5.7m.
14.解:过分别作、的垂线,设垂足为、,
则,,
在中,
斜坡的坡度,米,
设米,米,
,
,
米,米,
在中,,
米,
(米),
在中,(米),
(米).
答:宣传牌的高度为2米.
15.解:如图,过点P作PC垂直于AB所在直线,垂足为C,
根据题意可得,,
在中,,
在中,,
∴,
解得,
∵,
∴如果渔船不改变航向有触礁的危险,
∵,
∴若改变航向,刚好到暗礁区域边界时的,
此时,
即如果有危险,渔船自B处开始,沿南偏东小于45度的方向航行,能够安全通过这一海域.
16.(1)依题意可得,在中, ,
米,
米,米.
即之间的距离为30米.
(2)在中,,米,
(米),
米,米.
由.并精确到整数可得米.
即天线的高度约为27米.
17.解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
在Rt△ABD中,∵AB=10米,∠BAD=30°,
∴(米),(米),
在Rt△CDA中,∠CDA=90°,∠CAD=50°,
∴(米),
∴(米).
18.(1)∵,,
∴.
(2)过点作于,
由题意,,,
∴,
∴,
∴(海里),
在中,,
∴,
∵.
所以货船继续向正东方向行驶无触礁危险.
19.如图,在Rt△FGA中,
设AG=FG=x米,
在Rt△AEG中,=tan30°,
解得,x==4.05米,
∴AB=1.6+4.05=5.65米.
答:旗杆AB的高度为5.65米.
20.(1)能看到;
由题意得,∠DFG=90°-53°=37°,
则=tan∠DFG,
∵DF=4米,
∴DG=4×tan37°≈4×0.75=3(米),
故能看到这只老鼠;
(2)由(1)得,AG=AD+DG=2.7+3=5.7(米),
又=sin∠ACG=sin37°,
则CG==9.5(米),
答:要捕捉到这只老鼠,猫头鹰至少要飞约9.5米.
【模型三:拥抱型】
21.B
【分析】本题考査了解直角三角形的应用一仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
延长交于点C,根据题意得,然后在中,利用锐角三角函数的定义求出的长,从而求出的长,再在中,利用锐角三角函数的定义求出的长,最后利用线段的和差关系进行计算,即可解答.
【详解】如图,延长交于点C.
由题意得.
在中,,
,
.
在中,,
,
.
故选B.
22.58
【分析】本题考查了解直角三角形的应用一方向角问题,根据题意可得:海里,然后在中,利用锐角三角函数的定义求出的长,从而求出的长,再在中,利用锐角三角函数的定义求出的长,从而求的长.
【详解】解:由题意得:(海里),
在中,海里,
∴(海里)
(海里),
在中,,
∴(海里),
(海里),
即乙船向正东方向航行了58海里,
故答案为:58
23.(1)解:在中,米;
由 ,
得米;
又因为米,
因而大楼米,
答:楼高为米;
(2)解:∵在中,米,
,
∴米;
因而广告牌米;
答:广告牌的高度为米.
24.解:在Rt△ACD中,,则.
设,则
在Rt△BCD中,.
∴
∴
解得:.
在Rt△ACE中,.
∴
答:塑像“夸父追日”DE 的高度约为10.5米.
25.解:设为米,则米,∵ ∴,而米,
在中,,
则米,米,
在中,,
解得.
答:小山的高度为米.
26.(1)解:根据题意得:,,
在中,,
;
(2)解:过点D作,交延长线于点H,
,
,
,
设,则,
在中,
,
,
解得:,
,
,
四边形是矩形,
,
,
答:慈氏塔的高度为.
27.(1)解:由题意得,,,,米,米,
∴,
过点作于,则,
∴为等腰直角三角形,
∴米,
∴米,
∴米;
(2)解:∵,,,
∴米,米,
∴路线②的路程为米,
∴小宏到达景点的时间为分钟,
∵路线①的路程为米,
∴小明到达景点的时间为分钟,
∵,
∴小宏先到达景点.
28.(1)解:,
,
,
是等腰直角三角形,
,
在中,,,
,
;
故答案为:,2;
(2),
,
,
,
由题意可知,
,
,
在中,
,
,
即“美”字的高度约为.
29.(1)解:∵垂直于水平地面,
∴,
∵坡比,
∴,
设,则,
∵坡面长,
∴,
解得:,(负值舍去)
∴,,
∵,
∴,
由题意得:,
∴,
∵,
∴.
由题意得:,
∴,
∴.
(2)如图,过点作于点,于,
∴,
∴四边形是矩形,
∴,
∵叶片绕点顺时针转动,
∴,
∵,
∴,
由题意得:,
∴,
∴.
∴叶片顶端离水平地面的距离为.
30.(1)解:在中,,,
,
,
,
,
,
在中,,
,
该支架的边的长为;
(2)解:符合要求,过程如下:
过点作,垂足为,
∵,
∴四边形是矩形
则,,
在中,,,
,
,
,
,
,
,
在中,,
,
安装雨棚的高度是合格的.
【模型四:单一型】
31.解:由题知 , 四边形 是矩形,,,
∴.
在 中 ,
∴
∴ .
答:空调机的底部位置距离床的高度约为.
32.解:如图所示,过点作于H,
∵米,,米,米,
∴,米,米,
∴,
在中,米;
答:农夫所在的E处到地面的高度为米.
33.解:当,时,过点C作于F,过点A作于点M,则四边形是矩形,
∴,,
∵,
∴,
在中,,
∴,
∴,
∵,
∴该消防车能实施有效救援.
34.(1)解:过点作于点,过点作于点,
.
由题意得:,
四边形为矩形,
,.
,
.
,
.
.
答:支点离桌面的高度为;
(2)解:过点作,过点作于点,
.
,,
.
当时,;
当时,;
当从变化到的过程中,面板上端离桌面的高度是增加了,增加了约.
35.(1)解:如图,连接,延长交于点,
根据题意可得四边形是矩形,
∴,
∵,,
∴,,
∴,,
∴,
在中,由勾股定理得:,
∴视线距离的长为;
(2)解:如图,连接,延长交于点,
由题意可得:,,,,
在中,,即,
∴,
∴,
∴需要将支架调整到.
36.(1)解:由题意,知米,,
在中,
(米),
故答案为:976;
(2)解:选择方案一更合理.
理由:在中,
(米),
方案一需要时间为:,
方案二需要时间为:,
,
选择方案一更合理.
37.(1)解:根据题意得:(米),
故答案为:8;
(2)由题意可知,,
∴,
∴(米),
∴(米),
答:小汽车从点B开始减速到停下这一段的行驶的距离为31米.
38.解:如图所示,过点A作地面的垂线,垂足为B,亮亮的位置用表示,过点D作于C,则四边形是矩形,
∴米,米,
在中,米,,
∴米,
∴米,
答:无人机距离地面的高度约为米.
39.解:过点作,垂足为,
,
四边形是矩形,
,,
,
,
在中,,
,
,
云梯消防车最高点距离地面的高度为.
40.如图,延长交于点H.
,
,
,
四边形是矩形,
,
.
在中,
,
,
答:云梯顶端A到地面的距离的长约为.
