9.1.1 生活中的轴对称 课件(共25张PPT)
文档属性
| 名称 | 9.1.1 生活中的轴对称 课件(共25张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 18:56:50 | ||
图片预览







文档简介
(共25张PPT)
(华师大版)七年级
下
9.1.1生活中的轴对称
轴对称、平移与旋转
第9章
“九”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.了解轴对称图形和两个图形成轴对称的概念,知道二者之间的区别与联系.
2.能识别轴对称图形、两个图形成轴对称及其对称轴.
3.通过具体实例,类比思考,抽象出轴对称图形和成轴对称的特征.
新知导入
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见,山倒映在湖中,这是令人难忘的对称景象。自远古以来,对称的形式都被认为是和谐美丽的.
新知导入
观察下图中的几组图片和图形,它们有什么共同特点?
将上图中的每一个图形沿某条直线对折,直线两旁的部分能完全重合吗?
新知讲解
概括:
把一个图形沿某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
对称轴
对称轴要用虚线表示
一个图形
完全重合
有对称轴
新知讲解
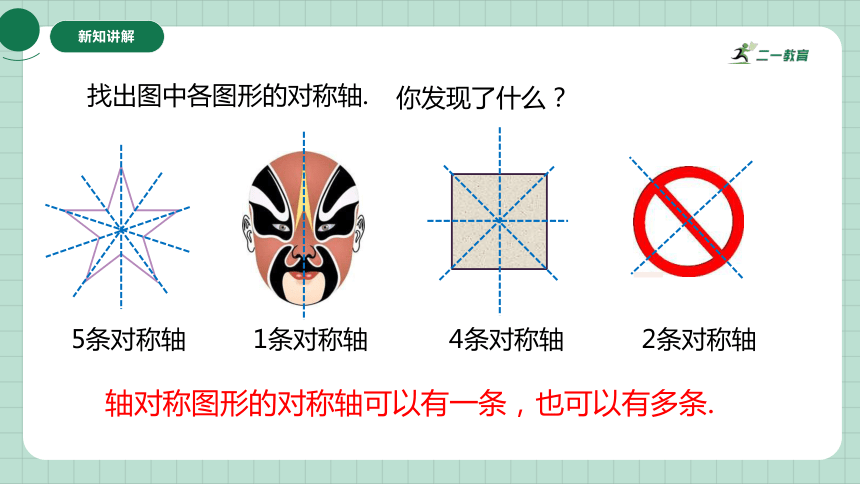
5条对称轴
1条对称轴
4条对称轴
2条对称轴
找出图中各图形的对称轴.
你发现了什么?
轴对称图形的对称轴可以有一条,也可以有多条.
新知讲解
试一试:用一张半透明的纸描出如图所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有多少条对称轴.
新知讲解
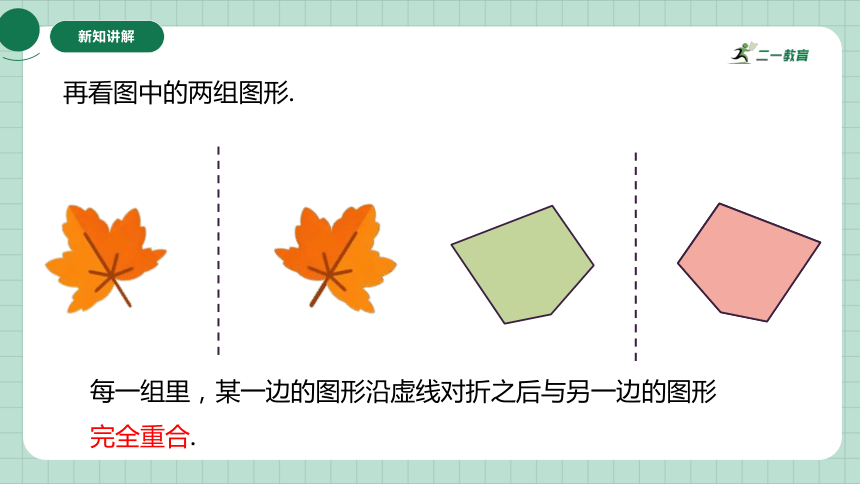
再看图中的两组图形.
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
新知讲解
概括:
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
新知讲解
两个图形成轴对称与轴对称图形的区别与联系
名称 两个图形成轴对称 轴对称图形
区别 1 对象不同 两个图形 一个图形
2 意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
3 对称点位置不同 对称点分别在两个图形上 对称点在同一个图形上
新知讲解
两个图形成轴对称与轴对称图形的区别与联系
名称 两个图形成轴对称 轴对称图形
区别 4 对称轴位置 不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 对称轴一定经过这个图形的内部
5 对称轴数量 不同 只有一条 有一条、多条或无数条
新知讲解
请你标出图中A、B、C三点的对称点A1、B1、C1.
A
C
B
A1
B1
C1
两个图形重合时相互重合的点叫做对应点,又叫对称点.
对折后重合的线段叫做对应线段,如AB与A1B1.
对折后重合的角叫做对应角,如∠A与∠A1.
轴对称图形(或成轴对称的两个图形)的对应线段和对应角有什么关系?
新知讲解
概括:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
轴对称
图形的基本特征.
对应角:∠A=∠A1,∠B=∠B1,∠C=∠C1
对应线段:
AB= A1B1,BC= B1C1
A
C
B
A1
B1
C1
【知识技能类作业】必做题:
课堂练习
1.中国古典建筑中有着丰富多彩的装饰纹样,以下四个纹样中,不是轴对称图形的是( )
A
A. B. C. D.
【知识技能类作业】必做题:
课堂练习
2.如图,直线是四边形的对称轴.若,,则 的度数为_____.
92°
【知识技能类作业】必做题:
课堂练习
3.如图,和关于直线对称,点 ,,的对称点分别为
点,,, , ,,求的度数和
的长度.
解: , ,
.
【知识技能类作业】选做题:
课堂练习
4.如图,直线MN是四边形AMBN的对称轴,P是直线MN上的点,下列判断错误的是( )
A. AM=BM B. ∠MAP=∠MBP
C. AP=BN D. ∠ANM=∠BNM
C
【知识技能类作业】选做题:
课堂练习
5.如图,若左边的五边形与右边的五边形关于中间的虚线对称,则∠α的度数为 .
65°
【综合拓展类作业】
课堂练习
6. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1) 指出△ABC与△ADE中的对称点.
(2) 指出△ABC与△ADE中相等的线段和角.
(3) 在不添加字母和线段的情况下,图中还有对称的三角形吗 如果有,请写出来.
解:(1) A与A、B与D、C与E是对称点
(2) AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,
∠C=∠E
(3) 有 △AFC与△AFE、△ABF与△ADF也都关于直线MN对称
课堂总结
1.轴对称图形:
把一个图形沿某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
2.两个图形成轴对称:
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
课堂总结
3.轴对称图形的基本特征:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
板书设计
1.轴对称图形:
2.两个图形成轴对称:
3.轴对称图形的基本特征:
课题:9.1.1生活中的轴对称
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
9.1.1生活中的轴对称
轴对称、平移与旋转
第9章
“九”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.了解轴对称图形和两个图形成轴对称的概念,知道二者之间的区别与联系.
2.能识别轴对称图形、两个图形成轴对称及其对称轴.
3.通过具体实例,类比思考,抽象出轴对称图形和成轴对称的特征.
新知导入
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见,山倒映在湖中,这是令人难忘的对称景象。自远古以来,对称的形式都被认为是和谐美丽的.
新知导入
观察下图中的几组图片和图形,它们有什么共同特点?
将上图中的每一个图形沿某条直线对折,直线两旁的部分能完全重合吗?
新知讲解
概括:
把一个图形沿某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
对称轴
对称轴要用虚线表示
一个图形
完全重合
有对称轴
新知讲解
5条对称轴
1条对称轴
4条对称轴
2条对称轴
找出图中各图形的对称轴.
你发现了什么?
轴对称图形的对称轴可以有一条,也可以有多条.
新知讲解
试一试:用一张半透明的纸描出如图所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有多少条对称轴.
新知讲解
再看图中的两组图形.
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
新知讲解
概括:
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
新知讲解
两个图形成轴对称与轴对称图形的区别与联系
名称 两个图形成轴对称 轴对称图形
区别 1 对象不同 两个图形 一个图形
2 意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
3 对称点位置不同 对称点分别在两个图形上 对称点在同一个图形上
新知讲解
两个图形成轴对称与轴对称图形的区别与联系
名称 两个图形成轴对称 轴对称图形
区别 4 对称轴位置 不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 对称轴一定经过这个图形的内部
5 对称轴数量 不同 只有一条 有一条、多条或无数条
新知讲解
请你标出图中A、B、C三点的对称点A1、B1、C1.
A
C
B
A1
B1
C1
两个图形重合时相互重合的点叫做对应点,又叫对称点.
对折后重合的线段叫做对应线段,如AB与A1B1.
对折后重合的角叫做对应角,如∠A与∠A1.
轴对称图形(或成轴对称的两个图形)的对应线段和对应角有什么关系?
新知讲解
概括:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
轴对称
图形的基本特征.
对应角:∠A=∠A1,∠B=∠B1,∠C=∠C1
对应线段:
AB= A1B1,BC= B1C1
A
C
B
A1
B1
C1
【知识技能类作业】必做题:
课堂练习
1.中国古典建筑中有着丰富多彩的装饰纹样,以下四个纹样中,不是轴对称图形的是( )
A
A. B. C. D.
【知识技能类作业】必做题:
课堂练习
2.如图,直线是四边形的对称轴.若,,则 的度数为_____.
92°
【知识技能类作业】必做题:
课堂练习
3.如图,和关于直线对称,点 ,,的对称点分别为
点,,, , ,,求的度数和
的长度.
解: , ,
.
【知识技能类作业】选做题:
课堂练习
4.如图,直线MN是四边形AMBN的对称轴,P是直线MN上的点,下列判断错误的是( )
A. AM=BM B. ∠MAP=∠MBP
C. AP=BN D. ∠ANM=∠BNM
C
【知识技能类作业】选做题:
课堂练习
5.如图,若左边的五边形与右边的五边形关于中间的虚线对称,则∠α的度数为 .
65°
【综合拓展类作业】
课堂练习
6. 如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1) 指出△ABC与△ADE中的对称点.
(2) 指出△ABC与△ADE中相等的线段和角.
(3) 在不添加字母和线段的情况下,图中还有对称的三角形吗 如果有,请写出来.
解:(1) A与A、B与D、C与E是对称点
(2) AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,
∠C=∠E
(3) 有 △AFC与△AFE、△ABF与△ADF也都关于直线MN对称
课堂总结
1.轴对称图形:
把一个图形沿某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
2.两个图形成轴对称:
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
课堂总结
3.轴对称图形的基本特征:
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
板书设计
1.轴对称图形:
2.两个图形成轴对称:
3.轴对称图形的基本特征:
课题:9.1.1生活中的轴对称
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
