【期中押题卷】北京市2024-2025学年六年级下学期期中综合测试数学试卷人教版(含解析)
文档属性
| 名称 | 【期中押题卷】北京市2024-2025学年六年级下学期期中综合测试数学试卷人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 910.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 10:28:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北京市2024-2025学年六年级下学期期中综合测试数学试卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2021秋 铁西区校级期末)从上面看,看到的形状是( )
A. B. C.
2.(2分)(2023春 陕州区期中)一成就是( )
A.1% B.10% C.100%
3.(2分)(2024春 巨野县期中)在一个比例里,两个内项互为倒数,两个外项的积是( )
A.0 B.1 C.5 D.10
4.(2分)(2022 北仑区)﹣0.5、、、25%分别对应直线上的四个点,距离0最远的是( )所对应的点。
A.﹣0.5 B. C. D.25%
5.(2分)(2024 高港区)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.不成比例 B.成反比例 C.成正比例 D.无法确定
6.(2分)(2023春 通榆县月考)李乐家住在17层,某天下班后他将汽车停在地下车库(﹣2层),然后乘电梯上楼。电梯需上升( )层他才能到家。
A.15 B.18 C.19
7.(2分)(2022 临沂)下列说法正确的是( )
A.圆锥的侧面展开是三角形
B.长方体、正方体、圆柱的体积都可以用底面积乘高来计算
C.半径为2厘米的圆的周长和面积相等
D.没有最大的正数,但有最大的负数
8.(2分)两件商品都卖了100元,但是由于每件的进价不同,使得一件赚了10%,另一件亏了10%。那么卖这两件商品是( )
A.赚了 B.亏了 C.不亏不赚
9.(2分)(2023 温岭市)将一个周长为12厘米的正方形变换成一个面积是36平方厘米的正方形,是按( )的比例放大的。
A.1:3 B.2:1 C.3:1 D.4:1
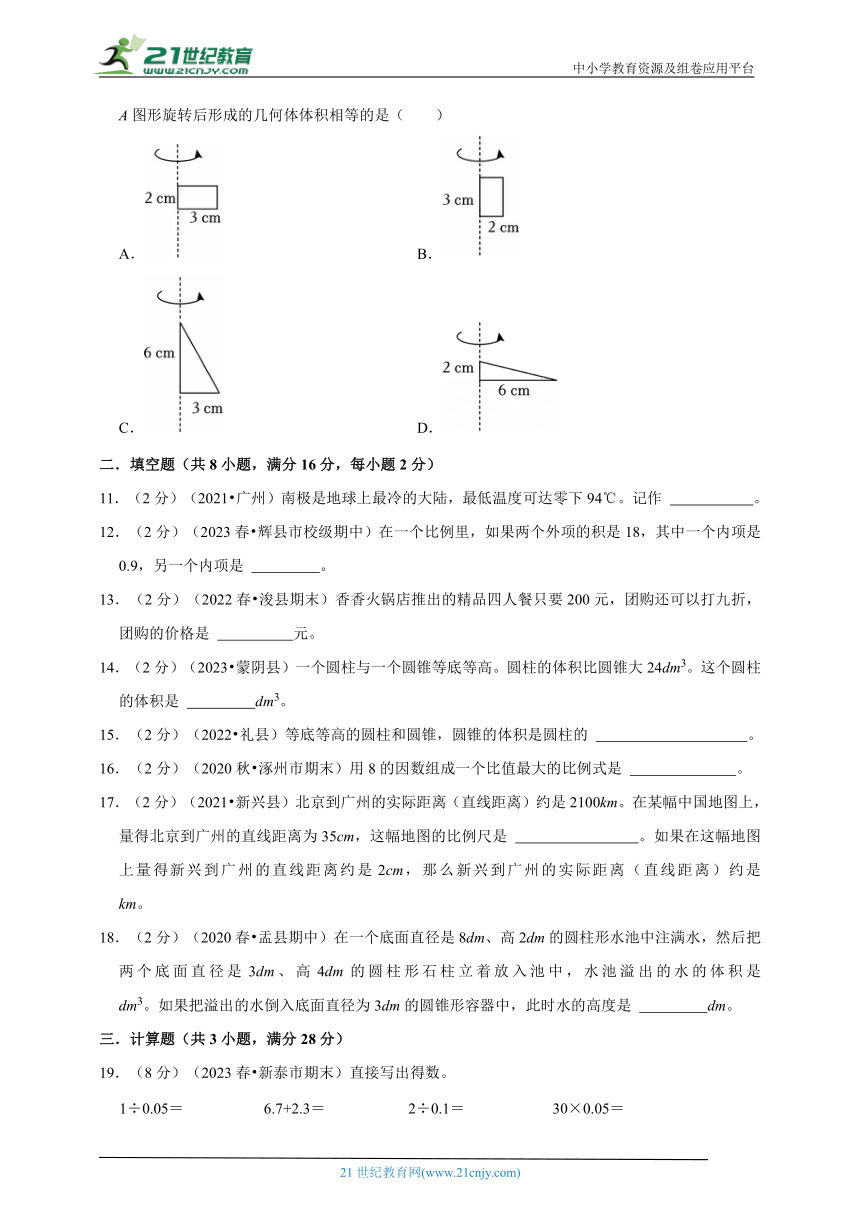
10.(2分)下面各图中的图形都以虚线为轴旋转一周,右边三个图形旋转后形成的几何体与最左边A图形旋转后形成的几何体体积相等的是( )
A. B.
C. D.
二.填空题(共8小题,满分16分,每小题2分)
11.(2分)(2021 广州)南极是地球上最冷的大陆,最低温度可达零下94℃。记作 。
12.(2分)(2023春 辉县市校级期中)在一个比例里,如果两个外项的积是18,其中一个内项是0.9,另一个内项是 。
13.(2分)(2022春 浚县期末)香香火锅店推出的精品四人餐只要200元,团购还可以打九折,团购的价格是 元。
14.(2分)(2023 蒙阴县)一个圆柱与一个圆锥等底等高。圆柱的体积比圆锥大24dm3。这个圆柱的体积是 dm3。
15.(2分)(2022 礼县)等底等高的圆柱和圆锥,圆锥的体积是圆柱的 。
16.(2分)(2020秋 涿州市期末)用8的因数组成一个比值最大的比例式是 。
17.(2分)(2021 新兴县)北京到广州的实际距离(直线距离)约是2100km。在某幅中国地图上,量得北京到广州的直线距离为35cm,这幅地图的比例尺是 。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是 km。
18.(2分)(2020春 盂县期中)在一个底面直径是8dm、高2dm的圆柱形水池中注满水,然后把两个底面直径是3dm、高4dm的圆柱形石柱立着放入池中,水池溢出的水的体积是 dm3。如果把溢出的水倒入底面直径为3dm的圆锥形容器中,此时水的高度是 dm。
三.计算题(共3小题,满分28分)
19.(8分)(2023春 新泰市期末)直接写出得数。
1÷0.05= 6.7+2.3= 2÷0.1= 30×0.05=
10﹣0.86= 80×25%= 4.8÷80%= 402=
20.(12分)(2022春 滨城区校级期中)解方程。
(1) (2)20%x+3.5=41.5
(3) (4)
21.(8分)(2022春 宛城区期中)(1)求圆柱的表面积和体积。
(2)求右面圆锥的体积。
四.操作题(共2小题,满分10分)
22.(6分)(2023秋 武汉期末)2023年9月26日,武汉光谷空轨旅游线正式运营了。小学五年级的淘气同学周末跟随爸爸、妈妈和爷爷(72岁)去乘坐“光谷光子号”,尽情体验了一次“人在空中游,景在窗外动”的科幻感。武汉光谷空轨旅游线规划总长26.7千米,目前开通一期工程,全长10.5千米,共设6个站点(如图),每隔10分钟发一趟车,行完全程约30分钟(九峰山——龙泉山或龙泉山——九峰山)。
(1)武汉光谷空轨旅游线还剩下百分之几没有完成?
(2)淘气家在高新四路站西偏南30°方向,在龙泉山西偏北30°方向上,请你在图中画出淘气家的位置。
(3)高新四路驿站按无障碍坡道的建设规范规定:坡道最大高度与水平长度的比为1:12(如图)设计轮椅坡道。高新四路站驿站进门处有5级台阶,每级台阶高0.15米,爷爷的轮椅经过的无障碍坡道的水平长度是多少米?
(4)淘气爸爸将车停在距离他家21.9千米的高新四路站,返回时,前15分钟行了全程的37.5%,之后因为前面出现交通事故而停留了15分钟。照这样计算,回到家一共要花多少分钟?
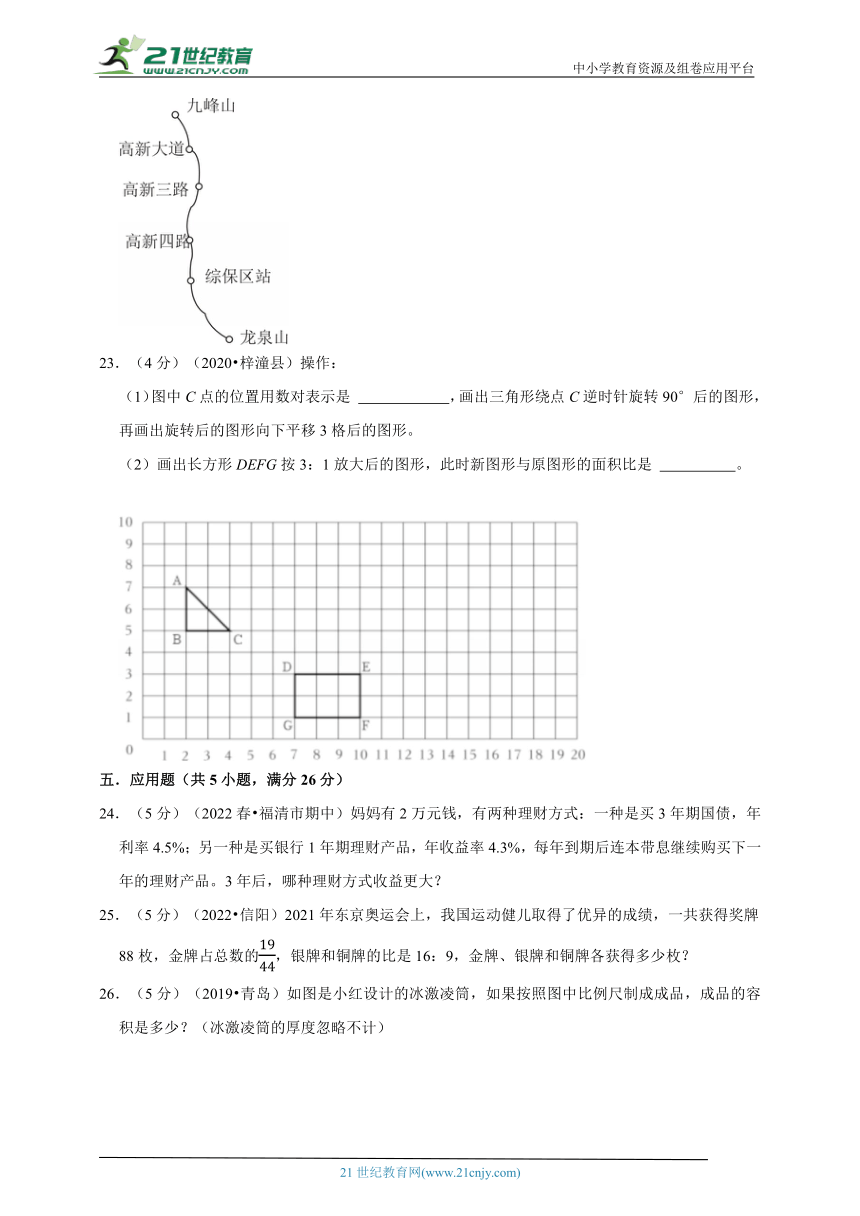
23.(4分)(2020 梓潼县)操作:
(1)图中C点的位置用数对表示是 ,画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是 。
五.应用题(共5小题,满分26分)
24.(5分)(2022春 福清市期中)妈妈有2万元钱,有两种理财方式:一种是买3年期国债,年利率4.5%;另一种是买银行1年期理财产品,年收益率4.3%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?
25.(5分)(2022 信阳)2021年东京奥运会上,我国运动健儿取得了优异的成绩,一共获得奖牌88枚,金牌占总数的,银牌和铜牌的比是16:9,金牌、银牌和铜牌各获得多少枚?
26.(5分)(2019 青岛)如图是小红设计的冰激凌筒,如果按照图中比例尺制成成品,成品的容积是多少?(冰激凌筒的厚度忽略不计)
27.(5分)(2022春 内乡县期末)滨河公园里有一个长方形的植物园,把植物园的长和宽分别缩小到原数的,画出了如图的示意图。这个植物园的面积是多少?
28.(6分)(2021 拱墅区模拟)圆珠笔5支一包的售51元,8支一包的售72元,张老师教的班上有49位小朋友,张老师要给每位小朋友1支笔,则张老师至少要花多少钱?
北京市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2021秋 铁西区校级期末)从上面看,看到的形状是( )
A. B. C.
【考点】圆柱的特征.
【专题】几何直观.
【答案】C
【分析】根据题意,从上面看,看到的形状是,据此解答即可。
【解答】解:从上面看,看到的形状是。
故选:C。
【点评】本题考查了从不同方向观察物体的知识,结合图示解答即可。
2.(2分)(2023春 陕州区期中)一成就是( )
A.1% B.10% C.100%
【考点】成数;百分数的意义、读写及应用.
【专题】应用意识.
【答案】B
【分析】根据成数的意义,一成就是,用百分数表示为10%,据此解答。
【解答】解:一成就是10%。
故选:B。
【点评】本题解题的关键是理解成数的意义。
3.(2分)(2024春 巨野县期中)在一个比例里,两个内项互为倒数,两个外项的积是( )
A.0 B.1 C.5 D.10
【考点】比例的意义和基本性质.
【专题】常规题型;能力层次.
【答案】B
【分析】根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。利用倒数的意义可知,两个内项互为倒数,则两个外项也互为倒数.则两个外项的乘积是1。
【解答】解:根据比例的基本性质可知,两个内项互为倒数,两个外项的积是1。
故选:B。
【点评】本题主要考查比的基本性质和倒数的意义。
4.(2分)(2022 北仑区)﹣0.5、、、25%分别对应直线上的四个点,距离0最远的是( )所对应的点。
A.﹣0.5 B. C. D.25%
【考点】负数的意义及其应用.
【专题】数感.
【答案】A
【分析】正数位于原点(0点)的右边,负数位于左边,一个数去掉性质符号就表示该数表示的点到原点(0点)的距离,只要比较这三个数去掉性质符号后的大小即可判定哪个点最接近0。
【解答】解:25%<0.5
距离0最远的是﹣0.5所对应的点。
故选:A。
【点评】一个数的性质符号只表示它表示的点在原点(0点)的哪边,不能表示该点距原点(0点)的远近。
5.(2分)(2024 高港区)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.不成比例 B.成反比例 C.成正比例 D.无法确定
【考点】辨识成正比例的量与成反比例的量.
【专题】综合判断题;推理能力.
【答案】C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:平行四边形的面积:高=底(一定),比值一定,所以平行四边形的面积和高成正比例关系。
故选:C。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
6.(2分)(2023春 通榆县月考)李乐家住在17层,某天下班后他将汽车停在地下车库(﹣2层),然后乘电梯上楼。电梯需上升( )层他才能到家。
A.15 B.18 C.19
【考点】负数的意义及其应用.
【专题】数感.
【答案】B
【分析】用正负数表示意义相反的两种量:高于地面的层数记作正,则低于地面的层数就记作负。用高层数减去1求得地上要走得层数,再加上地下的两层即为所求。
【解答】解:17﹣1+2
=16+2
=18(层)
答:电梯需上升18层他才能到家。
故选:B。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
7.(2分)(2022 临沂)下列说法正确的是( )
A.圆锥的侧面展开是三角形
B.长方体、正方体、圆柱的体积都可以用底面积乘高来计算
C.半径为2厘米的圆的周长和面积相等
D.没有最大的正数,但有最大的负数
【考点】圆锥的体积;正、负数大小的比较;圆锥的特征;圆、圆环的面积;圆柱的侧面积、表面积和体积.
【专题】空间观念;几何直观;推理能力;应用意识.
【答案】B
【分析】A、圆锥的侧面展开是扇形,据此判断。
B、长方体、正方体、圆柱的体积公式都是:V=Sh,据此判断。
C、根据周长和面积的意义,围成封闭图形一周的长叫做周长,围成平面的大小叫做面积,因为周长和面积不是同类量,所以无法进行比较。据此判断。
D、根据正负数的意义,没有最大的正数,也没有最大的负数。据此判断。
【解答】解:由分析得:
A、圆锥的侧面展开是三角形。说法错误。
B、长方体、正方体、圆柱的体积都可以用底面积乘高来计算。说法正确。
C、半径为2厘米的圆的周长和面积相等,说法错误。
D、没有最大的正数,但有最大的负数。说法错误。
故选:B。
【点评】此题考查的目的是理解掌握圆锥侧面展开图的特征,长方体、正方体、圆柱的体积公式,周长和面积的意义、正负数的意义及应用。
8.(2分)两件商品都卖了100元,但是由于每件的进价不同,使得一件赚了10%,另一件亏了10%。那么卖这两件商品是( )
A.赚了 B.亏了 C.不亏不赚
【考点】百分数的实际应用.
【专题】运算能力.
【答案】B
【分析】把这种商品的进价看作单位“1”,赚了10%的商品的卖价是进价的(1+10%),亏了10%的卖出价是进价的(1﹣10%),根据百分数除法的意义,即可求出这两件商品的总进价,再与卖出总价进行比较,即可确定商店是亏了还是赚了。
【解答】解:两件商品的总进价为:
100÷(1+10%)+100÷(1﹣10%)
=100÷110%+100÷90%
≈91+111
=202(元)
两件商品的总卖价为:
100×2=200(元)
因为200<202,所以亏了。
答:商店亏了。
故选:B。
【点评】此题主要是考查百分数的实际应用。亏了还是赚,是看这两件商品的总进价总卖价而言的,关键是求出总进从与总卖价,而求总进价的关键是找单位“1”,进一步发现比单位“1”多或少百分之几,再根据百分数除法的意义来求。
9.(2分)(2023 温岭市)将一个周长为12厘米的正方形变换成一个面积是36平方厘米的正方形,是按( )的比例放大的。
A.1:3 B.2:1 C.3:1 D.4:1
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】B
【分析】根据正方形的周长计算公式“C=4a”即可求出周长是12厘米的正方形边长;由于36=6×6,根据正方形的面积计算公式“S=a2”即可求出变换成面积为36平方厘米的正方形的边长。然后根据图形放大与缩小的意义,用面积是36平方厘米的正方形边长比周长是12厘米的正方形边长即可。
【解答】解:12÷4=3(厘米)
即周长是12厘米的正方形边长是3厘米;
因为36=6×6
所以面积是36平方厘米的正方形边长是6厘米;
6:3=2:1
答:是按2:1的比例放大的。
故选:B。
【点评】图形放大与缩小的倍数是指对应边放大或缩小的倍数;本题关键是求出原正方形、变换后正方形的边长。
10.(2分)下面各图中的图形都以虚线为轴旋转一周,右边三个图形旋转后形成的几何体与最左边A图形旋转后形成的几何体体积相等的是( )
A. B.
C. D.
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积页相等时圆锥的高是圆柱高的3倍,据此解答即可。
【解答】解:A旋转后得到一个底面半径是3厘米,高是2厘米的圆柱;
C旋转后得到一个底面半径是3厘米 高是6厘米的圆锥,因为C得到额圆锥的底面积与A得到的圆柱的底面积相等,C得到的圆锥的高是A得到的圆柱的高的3倍,所以它们的体积相等。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
二.填空题(共8小题,满分16分,每小题2分)
11.(2分)(2021 广州)南极是地球上最冷的大陆,最低温度可达零下94℃。记作 ﹣94℃ 。
【考点】负数的意义及其应用.
【专题】数感.
【答案】﹣94℃。
【分析】温度高于0℃记作正,则低于0℃就记作负。
【解答】解:南极是地球上最冷的大陆,最低温度可达零下94℃。记作﹣94℃。
故答案为:﹣94℃。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
12.(2分)(2023春 辉县市校级期中)在一个比例里,如果两个外项的积是18,其中一个内项是0.9,另一个内项是 20 。
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】见试题解答内容
【分析】根据比例的基本性质,内项积等于外项积,则用两个外项的积除以一个内项即可求出另一个内项。
【解答】解:18÷0.9=20
则另一个内项是20。
故答案为:20。
【点评】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
13.(2分)(2022春 浚县期末)香香火锅店推出的精品四人餐只要200元,团购还可以打九折,团购的价格是 180 元。
【考点】百分数的实际应用.
【专题】运算能力.
【答案】180。
【分析】打九折即表示现价是原价的90%,用乘法计算即可。
【解答】解:200×90%=180(元)
答:团购的价格是180元。
故答案为:180。
【点评】本题考查了百分数乘法应用题,关键是确定单位“1”,解答依据是:求一个数的百分之几是多少,用乘法计算。
14.(2分)(2023 蒙阴县)一个圆柱与一个圆锥等底等高。圆柱的体积比圆锥大24dm3。这个圆柱的体积是 36 dm3。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】36。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(3﹣1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
【解答】解:24÷(3﹣1)×3
=24÷2×3
=12×3
=36(dm3)
答:圆柱的体积是36dm3。
故答案为:36。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
15.(2分)(2022 礼县)等底等高的圆柱和圆锥,圆锥的体积是圆柱的 。
【考点】圆锥的体积.
【专题】空间观念;推理能力;应用意识.
【答案】。
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【解答】解:等底等高的圆柱和圆锥,圆锥的体积是圆柱的。
故答案为:。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
16.(2分)(2020秋 涿州市期末)用8的因数组成一个比值最大的比例式是 8:2=4:1 。
【考点】比例的意义和基本性质.
【专题】推理能力.
【答案】8:2=4:1。
【分析】找配对方法找出8的因数,8=1×8=2×4,据此利用比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,根据比值最大,解答即可。
【解答】解:因为8×1=4×2,所以8:2=4:1。
故答案为:8:2=4:1。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
17.(2分)(2021 新兴县)北京到广州的实际距离(直线距离)约是2100km。在某幅中国地图上,量得北京到广州的直线距离为35cm,这幅地图的比例尺是 1:6000000 。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是 120 km。
【考点】比例尺.
【专题】应用意识.
【答案】1:6000000;120。
【分析】由依据“比例尺=图上距离:实际距离”即可求出这幅地图的比例尺;再根据“实际距离=图上距离÷比例尺”即可求出新兴到广州的实际距离。
【解答】解:2100千米=210000000厘米
则35厘米:210000000厘米=1:6000000
212000000(厘米)
12000000厘米=120千米
答:这幅地图的比例尺是1:6000000。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是120km。
故答案为:1:6000000;120。
【点评】此题主要考查线段比例尺和数值比例尺的意义,以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
18.(2分)(2020春 盂县期中)在一个底面直径是8dm、高2dm的圆柱形水池中注满水,然后把两个底面直径是3dm、高4dm的圆柱形石柱立着放入池中,水池溢出的水的体积是 28.26 dm3。如果把溢出的水倒入底面直径为3dm的圆锥形容器中,此时水的高度是 12 dm。
【考点】圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】28.26,12。
【分析】根据题意,溢出水的体积就是石柱浸入水的体积,石柱浸入水中的高为2分米,根据圆柱的体积公式:V=πr2h,把数据代入公式求出溢出水的体积;因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆锥的高是圆柱高的3倍。据此解答即可。
【解答】解:3.14×(3÷2)2×2×2
=3.14×2.25×2×2
=14.13×2
=28.26(立方分米)
2×3×2=12(分米)
答:水池溢出的水的体积是28.26立方分米,此时水的高度是12分米。
故答案为:28.26,12。
【点评】此题主要考查圆柱的体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
三.计算题(共3小题,满分28分)
19.(8分)(2023春 新泰市期末)直接写出得数。
1÷0.05= 6.7+2.3= 2÷0.1= 30×0.05=
10﹣0.86= 80×25%= 4.8÷80%= 402=
【考点】整数、分数、小数、百分数四则混合运算;小数的加法和减法;小数乘法;小数除法;分数的加法和减法;分数乘法;分数除法.
【专题】运算能力.
【答案】20;9;20;1.5;9.14;20;6;1600;;;;。
【分析】根据小数、整数、分数、百分数加减乘除法的计算方法,直接进行口算即可。
【解答】解:
1÷0.05=20 6.7+2.3=9 2÷0.1=20 30×0.05=1.5
10﹣0.86=9.14 80×25%=20 4.8÷80%=6 402=1600
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
20.(12分)(2022春 滨城区校级期中)解方程。
(1) (2)20%x+3.5=41.5
(3) (4)
【考点】百分数方程求解.
【专题】简易方程;运算能力.
【答案】(1)x=24;(2)x=190;(3)x;(4)x=40。
【分析】(1)首先化简,然后根据等式的性质,两边同时乘2即可。
(2)首先根据等式的性质,两边同时减去3.5,然后两边再同时乘5即可。
(3)首先根据比例的基本性质化简,然后根据等式的性质,两边同时乘3即可。
(4)首先化简,然后根据等式的性质,两边同时除以0.3即可。
【解答】解:(1)
0.5x=12
0.5x×2=12×2
x=24
(2)20%x+3.5=41.5
0.2x+3.5﹣3.5=41.5﹣3.5
0.2x=38
0.2x×5=38×5
x=190
(3)
x4
x
x×33
x
(4)
0.3x=12
0.3x÷0.3=12÷0.3
x=40
【点评】此题主要考查了根据等式的性质解方程,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等;以及解比例问题,注意比例的基本性质的应用。
21.(8分)(2022春 宛城区期中)(1)求圆柱的表面积和体积。
(2)求右面圆锥的体积。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】空间观念;应用意识.
【答案】(1)87.92平方厘米,62.8立方厘米;
(2)314立方厘米。
【分析】(1)根据圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆锥的体积公式:Vr2h,把数据代入公式解答。
【解答】解(1)2×3.14×2×5+3.14×22×2
=12.56×5+3.14×4×2
=62.8+25.12
=87.92(平方厘米)
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(立方厘米)
答:这个圆柱的表面积是87.92平方厘米,体积是62.8立方厘米。
(2)3.14×(10÷2)2×12
3.14×25×12
=314(立方厘米)
答:这个圆锥的体积是314立方厘米。
【点评】此题主要考查圆柱的表面积公式、体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
四.操作题(共2小题,满分10分)
22.(6分)(2023秋 武汉期末)2023年9月26日,武汉光谷空轨旅游线正式运营了。小学五年级的淘气同学周末跟随爸爸、妈妈和爷爷(72岁)去乘坐“光谷光子号”,尽情体验了一次“人在空中游,景在窗外动”的科幻感。武汉光谷空轨旅游线规划总长26.7千米,目前开通一期工程,全长10.5千米,共设6个站点(如图),每隔10分钟发一趟车,行完全程约30分钟(九峰山——龙泉山或龙泉山——九峰山)。
(1)武汉光谷空轨旅游线还剩下百分之几没有完成?
(2)淘气家在高新四路站西偏南30°方向,在龙泉山西偏北30°方向上,请你在图中画出淘气家的位置。
(3)高新四路驿站按无障碍坡道的建设规范规定:坡道最大高度与水平长度的比为1:12(如图)设计轮椅坡道。高新四路站驿站进门处有5级台阶,每级台阶高0.15米,爷爷的轮椅经过的无障碍坡道的水平长度是多少米?
(4)淘气爸爸将车停在距离他家21.9千米的高新四路站,返回时,前15分钟行了全程的37.5%,之后因为前面出现交通事故而停留了15分钟。照这样计算,回到家一共要花多少分钟?
【考点】比的应用;百分数的实际应用;在平面图上标出物体的位置;根据方向和距离确定物体的位置.
【专题】综合题;运算能力.
【答案】(1)60.67%;
(2);
(3)9米;
(4)55分钟。
【分析】(1)武汉光谷空轨旅游线还剩下百分之几没有完成=(规划总长﹣一期开通长度)÷规划总长×100%,由此列式计算;
(2)利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答;
(3)先计算出台阶的总高度,利用坡道最大高度与水平长度的比,计算爷爷的轮椅经过的无障碍坡道的水平长度是多少米;
(4)前15分钟行了全程的37.5%,剩下路程用时=15÷37.5%×(1﹣37.5%),回家一共用时=全程37.5%用的时间+剩下路程用的时间+因交通事故停留的时间,由此列式计算。
【解答】解:(1)(26.7﹣10.5)÷26.7×100%
=16.2÷26.7×100%
≈60.67%
答:武汉光谷空轨旅游线还剩下60.67%没有完成。
(2);
(3)0.15×5×12=9(米)
答:爷爷的轮椅经过的无障碍坡道的水平长度是9米。
(4)15÷37.5%×(1﹣37.5%)+15+15
=25+15+15
=55(分钟)
答:回到家一共要花55分钟。
【点评】本题考查的是根据方向和距离确定物体位置,百分数以及比的应用。
23.(4分)(2020 梓潼县)操作:
(1)图中C点的位置用数对表示是 (4,5) ,画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是 9:1 。
【考点】图形的放大与缩小;数对与位置.
【专题】几何直观.
【答案】(1)(4,5),画图如下;(2)9:1。画图如下:
【分析】①利用数对表示位置的方法标出C点位置即可;根据旋转的方法,把三角形的另外两个顶点A、B,绕C点顺时针旋转90°,即可得出旋转后的三角形;然后根据平移的方法,把旋转后的图形向下平移3格后画出图形即可。
②原来长方形的长是3,宽是2,把长方形DEFG按3:1放大后,长是3×3=9,宽是3×1=3,然后画出图形即可,此时新图形与原图形的面积比是9:1。
【解答】解:操作:
(1)图中C点的位置用数对表示是(4,5),画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。画图如下:
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是9:1。画图如下:
故答案为:(1)(4,5),画图如下;(2)9:1。画图如下:
【点评】本题考查了数对、旋转、平移、图形放大等知识,结合题意分析解答即可。
五.应用题(共5小题,满分26分)
24.(5分)(2022春 福清市期中)妈妈有2万元钱,有两种理财方式:一种是买3年期国债,年利率4.5%;另一种是买银行1年期理财产品,年收益率4.3%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?
【考点】存款利息与纳税相关问题.
【专题】分数百分数应用题;应用意识.
【答案】3年期国债。
【分析】要想知道哪种理财方式收益更大,最要看看到期利息的多少。本题中,本金是20000元,一种是买三年期的国债,年利率为4.5%.另一种年收益率4.3%,时间是存入1年后取出后连本带息再购买下一年的理财产品,分别求出两种理财方式所得到的利息,根据关系式:利息=本金×利率×存期,然后比较,解决问题。
【解答】解:①三年期:
20000×4.5%×3
=900×3
=2700(元)
②先买一年期,把本金和利息取出来合在一起,再存入一年,
20000×4.3%×1=860(元)
(20000+860)×4.3%×1
=20860×4.3%×1
=896.98(元)
(20000+896.98+860)×4.3%×1
=21756.98×4.3%×1
≈935.55(元)
896.98+860+935.55=2692.53(元)
因为2700元>2692.53元,所以3年期国债得到的利息多。
答:3年期国债收益更大。
【点评】此题属于利息问题,考查了关系式:利息=本金×利率×存期。
25.(5分)(2022 信阳)2021年东京奥运会上,我国运动健儿取得了优异的成绩,一共获得奖牌88枚,金牌占总数的,银牌和铜牌的比是16:9,金牌、银牌和铜牌各获得多少枚?
【考点】比的应用.
【专题】应用意识.
【答案】金牌38枚,银牌32枚,铜牌18枚。
【分析】把2021年东京奥运会上,我国运动健儿共获得奖牌的总枚数看作单位“1”,根据分数乘法的意义,用总枚数乘,就是获得金牌的枚数。总枚数减金牌枚数就是银牌和铜牌的枚数,再把银牌和铜牌枚数平均分成(16+9)份,先用除法求出1份的枚数,再用乘法分别求出16份(银牌)、9份(铜牌)的枚数。
【解答】解:8838(枚)
(88﹣38)÷(16+9)
=50÷25
=2(枚)
2×16=32(枚)
2×9=18(枚)
答:金牌获得38枚,银牌获得32枚,铜牌获得18枚。
【点评】根据分数乘法的意义,求出金牌的枚数后,也可再把银牌、铜牌的枚数看作单位“1”,把比转化成分数,再根据分数乘法的意义解答。
26.(5分)(2019 青岛)如图是小红设计的冰激凌筒,如果按照图中比例尺制成成品,成品的容积是多少?(冰激凌筒的厚度忽略不计)
【考点】关于圆锥的应用题.
【专题】数据分析观念.
【答案】见试题解答内容
【分析】根据圆锥的体积公式VSh,将数据代入求解即可。首先实际距离=图上距离÷比例尺,求出圆锥的实际底面直径、实际的高,再根据圆锥的体积(容积)公式:Vπr2h,把数据代入公式解答。
【解答】解:1
=1×6
=6(厘米)
1.5
=1.5×6
=9(厘米)
3.14×(6÷2)2×9
3.14×9×9
=84.78(立方厘米)
答:成品的容积是84.78立方厘米。
【点评】此题考查的目的是理解掌握比例尺的意义及应用,圆锥体积公式的灵活运用,关键是熟记公式。
27.(5分)(2022春 内乡县期末)滨河公园里有一个长方形的植物园,把植物园的长和宽分别缩小到原数的,画出了如图的示意图。这个植物园的面积是多少?
【考点】比例的应用.
【专题】应用意识.
【答案】1200平方米。
【分析】根据“实际距离=图上距离÷比例尺”分别求出这个长方形植物圆的长、宽,根据长方形的面积计算公式“长方形面积=长×宽”即可解答。
【解答】解:44000(cm)
4000cm=40m
33000(cm)
3000cm=30m
40×30=1200(m2)
答:这个植物园的面积是1200平方米。
【点评】关键是根据图上距离、实际距离、比例尺三者之间的关系求出这个植物园的实际长、宽。
28.(6分)(2021 拱墅区模拟)圆珠笔5支一包的售51元,8支一包的售72元,张老师教的班上有49位小朋友,张老师要给每位小朋友1支笔,则张老师至少要花多少钱?
【考点】最优化问题.
【专题】运算能力;应用意识.
【答案】462元。
【分析】5支一包的平均每支51÷5=10.2(元),8支一包的平均每支72÷8=9(元),尽量买8支一包,并且尽可能接近49支,据此进行解答。
【解答】解:51÷5=10.2(元),872÷8=9(元),9<10.2,尽量买8支一包,并且尽可能接近49支最省钱;
49÷8=6(包)……1(支)
方案一:购买6+1=7(包)8支一包的,需要72×7=504(元)
方案二:购买6包8支一包的,1包5支一包的,需要72×6+51=483(元)
方案三:购买5包8支一包的,2包5支一包的,需要72×5+51×2=462(元)
462<483<504
所以,购买5包8支一包的,2包5支一包的最省钱,最少需要462元。
答:张老师至少要花462元钱。
【点评】解答此类题目的关键是计算出每一种方案需要花的钱数,然后比较得出最佳方案。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北京市2024-2025学年六年级下学期期中综合测试数学试卷
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2021秋 铁西区校级期末)从上面看,看到的形状是( )
A. B. C.
2.(2分)(2023春 陕州区期中)一成就是( )
A.1% B.10% C.100%
3.(2分)(2024春 巨野县期中)在一个比例里,两个内项互为倒数,两个外项的积是( )
A.0 B.1 C.5 D.10
4.(2分)(2022 北仑区)﹣0.5、、、25%分别对应直线上的四个点,距离0最远的是( )所对应的点。
A.﹣0.5 B. C. D.25%
5.(2分)(2024 高港区)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.不成比例 B.成反比例 C.成正比例 D.无法确定
6.(2分)(2023春 通榆县月考)李乐家住在17层,某天下班后他将汽车停在地下车库(﹣2层),然后乘电梯上楼。电梯需上升( )层他才能到家。
A.15 B.18 C.19
7.(2分)(2022 临沂)下列说法正确的是( )
A.圆锥的侧面展开是三角形
B.长方体、正方体、圆柱的体积都可以用底面积乘高来计算
C.半径为2厘米的圆的周长和面积相等
D.没有最大的正数,但有最大的负数
8.(2分)两件商品都卖了100元,但是由于每件的进价不同,使得一件赚了10%,另一件亏了10%。那么卖这两件商品是( )
A.赚了 B.亏了 C.不亏不赚
9.(2分)(2023 温岭市)将一个周长为12厘米的正方形变换成一个面积是36平方厘米的正方形,是按( )的比例放大的。
A.1:3 B.2:1 C.3:1 D.4:1
10.(2分)下面各图中的图形都以虚线为轴旋转一周,右边三个图形旋转后形成的几何体与最左边A图形旋转后形成的几何体体积相等的是( )
A. B.
C. D.
二.填空题(共8小题,满分16分,每小题2分)
11.(2分)(2021 广州)南极是地球上最冷的大陆,最低温度可达零下94℃。记作 。
12.(2分)(2023春 辉县市校级期中)在一个比例里,如果两个外项的积是18,其中一个内项是0.9,另一个内项是 。
13.(2分)(2022春 浚县期末)香香火锅店推出的精品四人餐只要200元,团购还可以打九折,团购的价格是 元。
14.(2分)(2023 蒙阴县)一个圆柱与一个圆锥等底等高。圆柱的体积比圆锥大24dm3。这个圆柱的体积是 dm3。
15.(2分)(2022 礼县)等底等高的圆柱和圆锥,圆锥的体积是圆柱的 。
16.(2分)(2020秋 涿州市期末)用8的因数组成一个比值最大的比例式是 。
17.(2分)(2021 新兴县)北京到广州的实际距离(直线距离)约是2100km。在某幅中国地图上,量得北京到广州的直线距离为35cm,这幅地图的比例尺是 。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是 km。
18.(2分)(2020春 盂县期中)在一个底面直径是8dm、高2dm的圆柱形水池中注满水,然后把两个底面直径是3dm、高4dm的圆柱形石柱立着放入池中,水池溢出的水的体积是 dm3。如果把溢出的水倒入底面直径为3dm的圆锥形容器中,此时水的高度是 dm。
三.计算题(共3小题,满分28分)
19.(8分)(2023春 新泰市期末)直接写出得数。
1÷0.05= 6.7+2.3= 2÷0.1= 30×0.05=
10﹣0.86= 80×25%= 4.8÷80%= 402=
20.(12分)(2022春 滨城区校级期中)解方程。
(1) (2)20%x+3.5=41.5
(3) (4)
21.(8分)(2022春 宛城区期中)(1)求圆柱的表面积和体积。
(2)求右面圆锥的体积。
四.操作题(共2小题,满分10分)
22.(6分)(2023秋 武汉期末)2023年9月26日,武汉光谷空轨旅游线正式运营了。小学五年级的淘气同学周末跟随爸爸、妈妈和爷爷(72岁)去乘坐“光谷光子号”,尽情体验了一次“人在空中游,景在窗外动”的科幻感。武汉光谷空轨旅游线规划总长26.7千米,目前开通一期工程,全长10.5千米,共设6个站点(如图),每隔10分钟发一趟车,行完全程约30分钟(九峰山——龙泉山或龙泉山——九峰山)。
(1)武汉光谷空轨旅游线还剩下百分之几没有完成?
(2)淘气家在高新四路站西偏南30°方向,在龙泉山西偏北30°方向上,请你在图中画出淘气家的位置。
(3)高新四路驿站按无障碍坡道的建设规范规定:坡道最大高度与水平长度的比为1:12(如图)设计轮椅坡道。高新四路站驿站进门处有5级台阶,每级台阶高0.15米,爷爷的轮椅经过的无障碍坡道的水平长度是多少米?
(4)淘气爸爸将车停在距离他家21.9千米的高新四路站,返回时,前15分钟行了全程的37.5%,之后因为前面出现交通事故而停留了15分钟。照这样计算,回到家一共要花多少分钟?
23.(4分)(2020 梓潼县)操作:
(1)图中C点的位置用数对表示是 ,画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是 。
五.应用题(共5小题,满分26分)
24.(5分)(2022春 福清市期中)妈妈有2万元钱,有两种理财方式:一种是买3年期国债,年利率4.5%;另一种是买银行1年期理财产品,年收益率4.3%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?
25.(5分)(2022 信阳)2021年东京奥运会上,我国运动健儿取得了优异的成绩,一共获得奖牌88枚,金牌占总数的,银牌和铜牌的比是16:9,金牌、银牌和铜牌各获得多少枚?
26.(5分)(2019 青岛)如图是小红设计的冰激凌筒,如果按照图中比例尺制成成品,成品的容积是多少?(冰激凌筒的厚度忽略不计)
27.(5分)(2022春 内乡县期末)滨河公园里有一个长方形的植物园,把植物园的长和宽分别缩小到原数的,画出了如图的示意图。这个植物园的面积是多少?
28.(6分)(2021 拱墅区模拟)圆珠笔5支一包的售51元,8支一包的售72元,张老师教的班上有49位小朋友,张老师要给每位小朋友1支笔,则张老师至少要花多少钱?
北京市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.选择题(共10小题,满分20分,每小题2分)
1.(2分)(2021秋 铁西区校级期末)从上面看,看到的形状是( )
A. B. C.
【考点】圆柱的特征.
【专题】几何直观.
【答案】C
【分析】根据题意,从上面看,看到的形状是,据此解答即可。
【解答】解:从上面看,看到的形状是。
故选:C。
【点评】本题考查了从不同方向观察物体的知识,结合图示解答即可。
2.(2分)(2023春 陕州区期中)一成就是( )
A.1% B.10% C.100%
【考点】成数;百分数的意义、读写及应用.
【专题】应用意识.
【答案】B
【分析】根据成数的意义,一成就是,用百分数表示为10%,据此解答。
【解答】解:一成就是10%。
故选:B。
【点评】本题解题的关键是理解成数的意义。
3.(2分)(2024春 巨野县期中)在一个比例里,两个内项互为倒数,两个外项的积是( )
A.0 B.1 C.5 D.10
【考点】比例的意义和基本性质.
【专题】常规题型;能力层次.
【答案】B
【分析】根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质。利用倒数的意义可知,两个内项互为倒数,则两个外项也互为倒数.则两个外项的乘积是1。
【解答】解:根据比例的基本性质可知,两个内项互为倒数,两个外项的积是1。
故选:B。
【点评】本题主要考查比的基本性质和倒数的意义。
4.(2分)(2022 北仑区)﹣0.5、、、25%分别对应直线上的四个点,距离0最远的是( )所对应的点。
A.﹣0.5 B. C. D.25%
【考点】负数的意义及其应用.
【专题】数感.
【答案】A
【分析】正数位于原点(0点)的右边,负数位于左边,一个数去掉性质符号就表示该数表示的点到原点(0点)的距离,只要比较这三个数去掉性质符号后的大小即可判定哪个点最接近0。
【解答】解:25%<0.5
距离0最远的是﹣0.5所对应的点。
故选:A。
【点评】一个数的性质符号只表示它表示的点在原点(0点)的哪边,不能表示该点距原点(0点)的远近。
5.(2分)(2024 高港区)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.不成比例 B.成反比例 C.成正比例 D.无法确定
【考点】辨识成正比例的量与成反比例的量.
【专题】综合判断题;推理能力.
【答案】C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:平行四边形的面积:高=底(一定),比值一定,所以平行四边形的面积和高成正比例关系。
故选:C。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
6.(2分)(2023春 通榆县月考)李乐家住在17层,某天下班后他将汽车停在地下车库(﹣2层),然后乘电梯上楼。电梯需上升( )层他才能到家。
A.15 B.18 C.19
【考点】负数的意义及其应用.
【专题】数感.
【答案】B
【分析】用正负数表示意义相反的两种量:高于地面的层数记作正,则低于地面的层数就记作负。用高层数减去1求得地上要走得层数,再加上地下的两层即为所求。
【解答】解:17﹣1+2
=16+2
=18(层)
答:电梯需上升18层他才能到家。
故选:B。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
7.(2分)(2022 临沂)下列说法正确的是( )
A.圆锥的侧面展开是三角形
B.长方体、正方体、圆柱的体积都可以用底面积乘高来计算
C.半径为2厘米的圆的周长和面积相等
D.没有最大的正数,但有最大的负数
【考点】圆锥的体积;正、负数大小的比较;圆锥的特征;圆、圆环的面积;圆柱的侧面积、表面积和体积.
【专题】空间观念;几何直观;推理能力;应用意识.
【答案】B
【分析】A、圆锥的侧面展开是扇形,据此判断。
B、长方体、正方体、圆柱的体积公式都是:V=Sh,据此判断。
C、根据周长和面积的意义,围成封闭图形一周的长叫做周长,围成平面的大小叫做面积,因为周长和面积不是同类量,所以无法进行比较。据此判断。
D、根据正负数的意义,没有最大的正数,也没有最大的负数。据此判断。
【解答】解:由分析得:
A、圆锥的侧面展开是三角形。说法错误。
B、长方体、正方体、圆柱的体积都可以用底面积乘高来计算。说法正确。
C、半径为2厘米的圆的周长和面积相等,说法错误。
D、没有最大的正数,但有最大的负数。说法错误。
故选:B。
【点评】此题考查的目的是理解掌握圆锥侧面展开图的特征,长方体、正方体、圆柱的体积公式,周长和面积的意义、正负数的意义及应用。
8.(2分)两件商品都卖了100元,但是由于每件的进价不同,使得一件赚了10%,另一件亏了10%。那么卖这两件商品是( )
A.赚了 B.亏了 C.不亏不赚
【考点】百分数的实际应用.
【专题】运算能力.
【答案】B
【分析】把这种商品的进价看作单位“1”,赚了10%的商品的卖价是进价的(1+10%),亏了10%的卖出价是进价的(1﹣10%),根据百分数除法的意义,即可求出这两件商品的总进价,再与卖出总价进行比较,即可确定商店是亏了还是赚了。
【解答】解:两件商品的总进价为:
100÷(1+10%)+100÷(1﹣10%)
=100÷110%+100÷90%
≈91+111
=202(元)
两件商品的总卖价为:
100×2=200(元)
因为200<202,所以亏了。
答:商店亏了。
故选:B。
【点评】此题主要是考查百分数的实际应用。亏了还是赚,是看这两件商品的总进价总卖价而言的,关键是求出总进从与总卖价,而求总进价的关键是找单位“1”,进一步发现比单位“1”多或少百分之几,再根据百分数除法的意义来求。
9.(2分)(2023 温岭市)将一个周长为12厘米的正方形变换成一个面积是36平方厘米的正方形,是按( )的比例放大的。
A.1:3 B.2:1 C.3:1 D.4:1
【考点】图形的放大与缩小.
【专题】图形与变换;空间观念.
【答案】B
【分析】根据正方形的周长计算公式“C=4a”即可求出周长是12厘米的正方形边长;由于36=6×6,根据正方形的面积计算公式“S=a2”即可求出变换成面积为36平方厘米的正方形的边长。然后根据图形放大与缩小的意义,用面积是36平方厘米的正方形边长比周长是12厘米的正方形边长即可。
【解答】解:12÷4=3(厘米)
即周长是12厘米的正方形边长是3厘米;
因为36=6×6
所以面积是36平方厘米的正方形边长是6厘米;
6:3=2:1
答:是按2:1的比例放大的。
故选:B。
【点评】图形放大与缩小的倍数是指对应边放大或缩小的倍数;本题关键是求出原正方形、变换后正方形的边长。
10.(2分)下面各图中的图形都以虚线为轴旋转一周,右边三个图形旋转后形成的几何体与最左边A图形旋转后形成的几何体体积相等的是( )
A. B.
C. D.
【考点】圆锥的体积;圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】C
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积页相等时圆锥的高是圆柱高的3倍,据此解答即可。
【解答】解:A旋转后得到一个底面半径是3厘米,高是2厘米的圆柱;
C旋转后得到一个底面半径是3厘米 高是6厘米的圆锥,因为C得到额圆锥的底面积与A得到的圆柱的底面积相等,C得到的圆锥的高是A得到的圆柱的高的3倍,所以它们的体积相等。
故选:C。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
二.填空题(共8小题,满分16分,每小题2分)
11.(2分)(2021 广州)南极是地球上最冷的大陆,最低温度可达零下94℃。记作 ﹣94℃ 。
【考点】负数的意义及其应用.
【专题】数感.
【答案】﹣94℃。
【分析】温度高于0℃记作正,则低于0℃就记作负。
【解答】解:南极是地球上最冷的大陆,最低温度可达零下94℃。记作﹣94℃。
故答案为:﹣94℃。
【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
12.(2分)(2023春 辉县市校级期中)在一个比例里,如果两个外项的积是18,其中一个内项是0.9,另一个内项是 20 。
【考点】比例的意义和基本性质.
【专题】比和比例.
【答案】见试题解答内容
【分析】根据比例的基本性质,内项积等于外项积,则用两个外项的积除以一个内项即可求出另一个内项。
【解答】解:18÷0.9=20
则另一个内项是20。
故答案为:20。
【点评】本题考查比例的基本性质,明确内项积等于外项积是解题的关键。
13.(2分)(2022春 浚县期末)香香火锅店推出的精品四人餐只要200元,团购还可以打九折,团购的价格是 180 元。
【考点】百分数的实际应用.
【专题】运算能力.
【答案】180。
【分析】打九折即表示现价是原价的90%,用乘法计算即可。
【解答】解:200×90%=180(元)
答:团购的价格是180元。
故答案为:180。
【点评】本题考查了百分数乘法应用题,关键是确定单位“1”,解答依据是:求一个数的百分之几是多少,用乘法计算。
14.(2分)(2023 蒙阴县)一个圆柱与一个圆锥等底等高。圆柱的体积比圆锥大24dm3。这个圆柱的体积是 36 dm3。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;几何直观.
【答案】36。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积差相当于圆锥体积的(3﹣1)倍,根据已知一个数的几倍是多少,求这个数,用除法求出圆锥的体积,进而求出圆柱的体积。
【解答】解:24÷(3﹣1)×3
=24÷2×3
=12×3
=36(dm3)
答:圆柱的体积是36dm3。
故答案为:36。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
15.(2分)(2022 礼县)等底等高的圆柱和圆锥,圆锥的体积是圆柱的 。
【考点】圆锥的体积.
【专题】空间观念;推理能力;应用意识.
【答案】。
【分析】等底等高的圆锥的体积是圆柱体积的,据此解答即可。
【解答】解:等底等高的圆柱和圆锥,圆锥的体积是圆柱的。
故答案为:。
【点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
16.(2分)(2020秋 涿州市期末)用8的因数组成一个比值最大的比例式是 8:2=4:1 。
【考点】比例的意义和基本性质.
【专题】推理能力.
【答案】8:2=4:1。
【分析】找配对方法找出8的因数,8=1×8=2×4,据此利用比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,根据比值最大,解答即可。
【解答】解:因为8×1=4×2,所以8:2=4:1。
故答案为:8:2=4:1。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
17.(2分)(2021 新兴县)北京到广州的实际距离(直线距离)约是2100km。在某幅中国地图上,量得北京到广州的直线距离为35cm,这幅地图的比例尺是 1:6000000 。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是 120 km。
【考点】比例尺.
【专题】应用意识.
【答案】1:6000000;120。
【分析】由依据“比例尺=图上距离:实际距离”即可求出这幅地图的比例尺;再根据“实际距离=图上距离÷比例尺”即可求出新兴到广州的实际距离。
【解答】解:2100千米=210000000厘米
则35厘米:210000000厘米=1:6000000
212000000(厘米)
12000000厘米=120千米
答:这幅地图的比例尺是1:6000000。如果在这幅地图上量得新兴到广州的直线距离约是2cm,那么新兴到广州的实际距离(直线距离)约是120km。
故答案为:1:6000000;120。
【点评】此题主要考查线段比例尺和数值比例尺的意义,以及图上距离、实际距离和比例尺的关系,解答时要注意单位的换算。
18.(2分)(2020春 盂县期中)在一个底面直径是8dm、高2dm的圆柱形水池中注满水,然后把两个底面直径是3dm、高4dm的圆柱形石柱立着放入池中,水池溢出的水的体积是 28.26 dm3。如果把溢出的水倒入底面直径为3dm的圆锥形容器中,此时水的高度是 12 dm。
【考点】圆柱的体积.
【专题】空间观念;推理能力;应用意识.
【答案】28.26,12。
【分析】根据题意,溢出水的体积就是石柱浸入水的体积,石柱浸入水中的高为2分米,根据圆柱的体积公式:V=πr2h,把数据代入公式求出溢出水的体积;因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等,底面积也相等时,圆锥的高是圆柱高的3倍。据此解答即可。
【解答】解:3.14×(3÷2)2×2×2
=3.14×2.25×2×2
=14.13×2
=28.26(立方分米)
2×3×2=12(分米)
答:水池溢出的水的体积是28.26立方分米,此时水的高度是12分米。
故答案为:28.26,12。
【点评】此题主要考查圆柱的体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
三.计算题(共3小题,满分28分)
19.(8分)(2023春 新泰市期末)直接写出得数。
1÷0.05= 6.7+2.3= 2÷0.1= 30×0.05=
10﹣0.86= 80×25%= 4.8÷80%= 402=
【考点】整数、分数、小数、百分数四则混合运算;小数的加法和减法;小数乘法;小数除法;分数的加法和减法;分数乘法;分数除法.
【专题】运算能力.
【答案】20;9;20;1.5;9.14;20;6;1600;;;;。
【分析】根据小数、整数、分数、百分数加减乘除法的计算方法,直接进行口算即可。
【解答】解:
1÷0.05=20 6.7+2.3=9 2÷0.1=20 30×0.05=1.5
10﹣0.86=9.14 80×25%=20 4.8÷80%=6 402=1600
【点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
20.(12分)(2022春 滨城区校级期中)解方程。
(1) (2)20%x+3.5=41.5
(3) (4)
【考点】百分数方程求解.
【专题】简易方程;运算能力.
【答案】(1)x=24;(2)x=190;(3)x;(4)x=40。
【分析】(1)首先化简,然后根据等式的性质,两边同时乘2即可。
(2)首先根据等式的性质,两边同时减去3.5,然后两边再同时乘5即可。
(3)首先根据比例的基本性质化简,然后根据等式的性质,两边同时乘3即可。
(4)首先化简,然后根据等式的性质,两边同时除以0.3即可。
【解答】解:(1)
0.5x=12
0.5x×2=12×2
x=24
(2)20%x+3.5=41.5
0.2x+3.5﹣3.5=41.5﹣3.5
0.2x=38
0.2x×5=38×5
x=190
(3)
x4
x
x×33
x
(4)
0.3x=12
0.3x÷0.3=12÷0.3
x=40
【点评】此题主要考查了根据等式的性质解方程,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等;以及解比例问题,注意比例的基本性质的应用。
21.(8分)(2022春 宛城区期中)(1)求圆柱的表面积和体积。
(2)求右面圆锥的体积。
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】空间观念;应用意识.
【答案】(1)87.92平方厘米,62.8立方厘米;
(2)314立方厘米。
【分析】(1)根据圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,把数据代入公式解答。
(2)根据圆锥的体积公式:Vr2h,把数据代入公式解答。
【解答】解(1)2×3.14×2×5+3.14×22×2
=12.56×5+3.14×4×2
=62.8+25.12
=87.92(平方厘米)
3.14×22×5
=3.14×4×5
=12.56×5
=62.8(立方厘米)
答:这个圆柱的表面积是87.92平方厘米,体积是62.8立方厘米。
(2)3.14×(10÷2)2×12
3.14×25×12
=314(立方厘米)
答:这个圆锥的体积是314立方厘米。
【点评】此题主要考查圆柱的表面积公式、体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
四.操作题(共2小题,满分10分)
22.(6分)(2023秋 武汉期末)2023年9月26日,武汉光谷空轨旅游线正式运营了。小学五年级的淘气同学周末跟随爸爸、妈妈和爷爷(72岁)去乘坐“光谷光子号”,尽情体验了一次“人在空中游,景在窗外动”的科幻感。武汉光谷空轨旅游线规划总长26.7千米,目前开通一期工程,全长10.5千米,共设6个站点(如图),每隔10分钟发一趟车,行完全程约30分钟(九峰山——龙泉山或龙泉山——九峰山)。
(1)武汉光谷空轨旅游线还剩下百分之几没有完成?
(2)淘气家在高新四路站西偏南30°方向,在龙泉山西偏北30°方向上,请你在图中画出淘气家的位置。
(3)高新四路驿站按无障碍坡道的建设规范规定:坡道最大高度与水平长度的比为1:12(如图)设计轮椅坡道。高新四路站驿站进门处有5级台阶,每级台阶高0.15米,爷爷的轮椅经过的无障碍坡道的水平长度是多少米?
(4)淘气爸爸将车停在距离他家21.9千米的高新四路站,返回时,前15分钟行了全程的37.5%,之后因为前面出现交通事故而停留了15分钟。照这样计算,回到家一共要花多少分钟?
【考点】比的应用;百分数的实际应用;在平面图上标出物体的位置;根据方向和距离确定物体的位置.
【专题】综合题;运算能力.
【答案】(1)60.67%;
(2);
(3)9米;
(4)55分钟。
【分析】(1)武汉光谷空轨旅游线还剩下百分之几没有完成=(规划总长﹣一期开通长度)÷规划总长×100%,由此列式计算;
(2)利用平面图上方向规定:上北下南左西右东,依据题意结合图示去解答;
(3)先计算出台阶的总高度,利用坡道最大高度与水平长度的比,计算爷爷的轮椅经过的无障碍坡道的水平长度是多少米;
(4)前15分钟行了全程的37.5%,剩下路程用时=15÷37.5%×(1﹣37.5%),回家一共用时=全程37.5%用的时间+剩下路程用的时间+因交通事故停留的时间,由此列式计算。
【解答】解:(1)(26.7﹣10.5)÷26.7×100%
=16.2÷26.7×100%
≈60.67%
答:武汉光谷空轨旅游线还剩下60.67%没有完成。
(2);
(3)0.15×5×12=9(米)
答:爷爷的轮椅经过的无障碍坡道的水平长度是9米。
(4)15÷37.5%×(1﹣37.5%)+15+15
=25+15+15
=55(分钟)
答:回到家一共要花55分钟。
【点评】本题考查的是根据方向和距离确定物体位置,百分数以及比的应用。
23.(4分)(2020 梓潼县)操作:
(1)图中C点的位置用数对表示是 (4,5) ,画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是 9:1 。
【考点】图形的放大与缩小;数对与位置.
【专题】几何直观.
【答案】(1)(4,5),画图如下;(2)9:1。画图如下:
【分析】①利用数对表示位置的方法标出C点位置即可;根据旋转的方法,把三角形的另外两个顶点A、B,绕C点顺时针旋转90°,即可得出旋转后的三角形;然后根据平移的方法,把旋转后的图形向下平移3格后画出图形即可。
②原来长方形的长是3,宽是2,把长方形DEFG按3:1放大后,长是3×3=9,宽是3×1=3,然后画出图形即可,此时新图形与原图形的面积比是9:1。
【解答】解:操作:
(1)图中C点的位置用数对表示是(4,5),画出三角形绕点C逆时针旋转90°后的图形,再画出旋转后的图形向下平移3格后的图形。画图如下:
(2)画出长方形DEFG按3:1放大后的图形,此时新图形与原图形的面积比是9:1。画图如下:
故答案为:(1)(4,5),画图如下;(2)9:1。画图如下:
【点评】本题考查了数对、旋转、平移、图形放大等知识,结合题意分析解答即可。
五.应用题(共5小题,满分26分)
24.(5分)(2022春 福清市期中)妈妈有2万元钱,有两种理财方式:一种是买3年期国债,年利率4.5%;另一种是买银行1年期理财产品,年收益率4.3%,每年到期后连本带息继续购买下一年的理财产品。3年后,哪种理财方式收益更大?
【考点】存款利息与纳税相关问题.
【专题】分数百分数应用题;应用意识.
【答案】3年期国债。
【分析】要想知道哪种理财方式收益更大,最要看看到期利息的多少。本题中,本金是20000元,一种是买三年期的国债,年利率为4.5%.另一种年收益率4.3%,时间是存入1年后取出后连本带息再购买下一年的理财产品,分别求出两种理财方式所得到的利息,根据关系式:利息=本金×利率×存期,然后比较,解决问题。
【解答】解:①三年期:
20000×4.5%×3
=900×3
=2700(元)
②先买一年期,把本金和利息取出来合在一起,再存入一年,
20000×4.3%×1=860(元)
(20000+860)×4.3%×1
=20860×4.3%×1
=896.98(元)
(20000+896.98+860)×4.3%×1
=21756.98×4.3%×1
≈935.55(元)
896.98+860+935.55=2692.53(元)
因为2700元>2692.53元,所以3年期国债得到的利息多。
答:3年期国债收益更大。
【点评】此题属于利息问题,考查了关系式:利息=本金×利率×存期。
25.(5分)(2022 信阳)2021年东京奥运会上,我国运动健儿取得了优异的成绩,一共获得奖牌88枚,金牌占总数的,银牌和铜牌的比是16:9,金牌、银牌和铜牌各获得多少枚?
【考点】比的应用.
【专题】应用意识.
【答案】金牌38枚,银牌32枚,铜牌18枚。
【分析】把2021年东京奥运会上,我国运动健儿共获得奖牌的总枚数看作单位“1”,根据分数乘法的意义,用总枚数乘,就是获得金牌的枚数。总枚数减金牌枚数就是银牌和铜牌的枚数,再把银牌和铜牌枚数平均分成(16+9)份,先用除法求出1份的枚数,再用乘法分别求出16份(银牌)、9份(铜牌)的枚数。
【解答】解:8838(枚)
(88﹣38)÷(16+9)
=50÷25
=2(枚)
2×16=32(枚)
2×9=18(枚)
答:金牌获得38枚,银牌获得32枚,铜牌获得18枚。
【点评】根据分数乘法的意义,求出金牌的枚数后,也可再把银牌、铜牌的枚数看作单位“1”,把比转化成分数,再根据分数乘法的意义解答。
26.(5分)(2019 青岛)如图是小红设计的冰激凌筒,如果按照图中比例尺制成成品,成品的容积是多少?(冰激凌筒的厚度忽略不计)
【考点】关于圆锥的应用题.
【专题】数据分析观念.
【答案】见试题解答内容
【分析】根据圆锥的体积公式VSh,将数据代入求解即可。首先实际距离=图上距离÷比例尺,求出圆锥的实际底面直径、实际的高,再根据圆锥的体积(容积)公式:Vπr2h,把数据代入公式解答。
【解答】解:1
=1×6
=6(厘米)
1.5
=1.5×6
=9(厘米)
3.14×(6÷2)2×9
3.14×9×9
=84.78(立方厘米)
答:成品的容积是84.78立方厘米。
【点评】此题考查的目的是理解掌握比例尺的意义及应用,圆锥体积公式的灵活运用,关键是熟记公式。
27.(5分)(2022春 内乡县期末)滨河公园里有一个长方形的植物园,把植物园的长和宽分别缩小到原数的,画出了如图的示意图。这个植物园的面积是多少?
【考点】比例的应用.
【专题】应用意识.
【答案】1200平方米。
【分析】根据“实际距离=图上距离÷比例尺”分别求出这个长方形植物圆的长、宽,根据长方形的面积计算公式“长方形面积=长×宽”即可解答。
【解答】解:44000(cm)
4000cm=40m
33000(cm)
3000cm=30m
40×30=1200(m2)
答:这个植物园的面积是1200平方米。
【点评】关键是根据图上距离、实际距离、比例尺三者之间的关系求出这个植物园的实际长、宽。
28.(6分)(2021 拱墅区模拟)圆珠笔5支一包的售51元,8支一包的售72元,张老师教的班上有49位小朋友,张老师要给每位小朋友1支笔,则张老师至少要花多少钱?
【考点】最优化问题.
【专题】运算能力;应用意识.
【答案】462元。
【分析】5支一包的平均每支51÷5=10.2(元),8支一包的平均每支72÷8=9(元),尽量买8支一包,并且尽可能接近49支,据此进行解答。
【解答】解:51÷5=10.2(元),872÷8=9(元),9<10.2,尽量买8支一包,并且尽可能接近49支最省钱;
49÷8=6(包)……1(支)
方案一:购买6+1=7(包)8支一包的,需要72×7=504(元)
方案二:购买6包8支一包的,1包5支一包的,需要72×6+51=483(元)
方案三:购买5包8支一包的,2包5支一包的,需要72×5+51×2=462(元)
462<483<504
所以,购买5包8支一包的,2包5支一包的最省钱,最少需要462元。
答:张老师至少要花462元钱。
【点评】解答此类题目的关键是计算出每一种方案需要花的钱数,然后比较得出最佳方案。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
