新人教版数学五年级下册7.1折线统计图课时练习
文档属性
| 名称 | 新人教版数学五年级下册7.1折线统计图课时练习 |  | |
| 格式 | doc | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-12 11:51:51 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新人教版数学五年级下册第七章7.1折线统计图课时练习
一、选择题(共15小题)
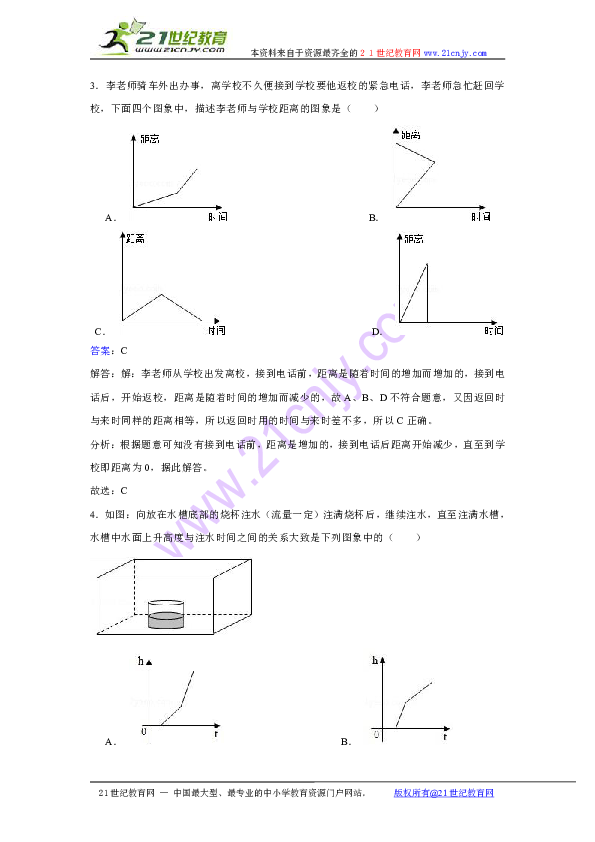
1.在常见的折线统计图上,表示( )
A. 不变 B. 缓慢上升 C. 缓慢下降 D. 大幅上升
答案:B
解答:解:在常见的折线统计图上,表示缓慢上升;
分析:折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;如图所示的情况,属于缓慢上升,据此解答即可。
故选:B
2.从家去图书馆,中途休息了几分钟,借完书后直接回家.能描述这一过程图象的是( )
A. B.
C. D.
答案:A
解答:解:小红的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到图书馆,这一段时间里离家的距离越来越远;
(4)在图书馆借书,这一段时间离家的距离不变;
(5)从图书馆回家,这一段时间里离家的距离越来越近。
只有选项A符合这一变化。
分析:根据所给的条件,解析出时间与离家距离之间的关系,再从选项中找出符合的答案。
故选:A
3.李老师骑车外出办事,离学校不久便接到学校要他返校的紧急电话,李老师急忙赶回学校,下面四个图象中,描述李老师与学校距离的图象是( )
A. B.
C. D.
答案:C
解答:解:李老师从学校出发离校,接到电话前,距离是随着时间的增加而增加的,接到电话后,开始返校,距离是随着时间的增加而减少的,故A、B、D不符合题意,又因返回时与来时同样的距离相等,所以返回时用的时间与来时差不多,所以C正确。
分析:根据题意可知没有接到电话前,距离是增加的,接到电话后距离开始减少,直至到学校即距离为0,据此解答。
故选:C
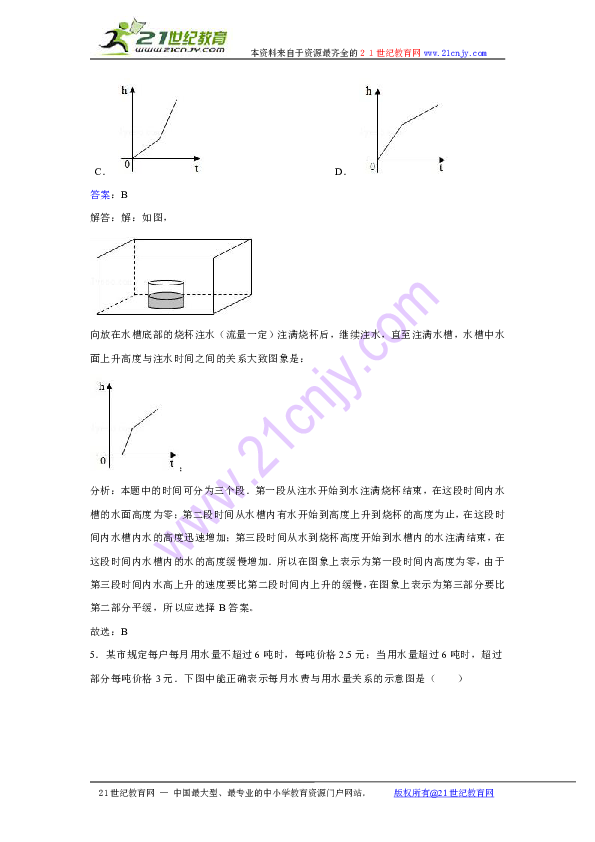
4.如图:向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致是下列图象中的( )
A. B.
C. D.
答案:B
解答:解:如图,
向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致图象是:
;
分析:本题中的时间可分为三个段.第一段从注水开始到水注满烧杯结束,在这段时间内水槽的水面高度为零;第二段时间从水槽内有水开始到高度上升到烧杯的高度为止,在这段时间内水槽内水的高度迅速增加;第三段时间从水到烧杯高度开始到水槽内的水注满结束,在这段时间内水槽内的水的高度缓慢增加.所以在图象上表示为第一段时间内高度为零,由于第三段时间内水高上升的速度要比第二段时间内上升的缓慢,在图象上表示为第三部分要比第二部分平缓,所以应选择B答案。
故选:B
5.某市规定每户每月用水量不超过6吨时,每吨价格2.5元;当用水量超过6吨时,超过部分每吨价格3元.下图中能正确表示每月水费与用水量关系的示意图是( )
A. B. C. D.
答案:C
解答:解:由解析知:每户每月用水量不超过6吨,每吨价格为2.5元;当用水量超过6吨时,超过部分每吨价格为3元.下面3幅图中能表示每月水费与用水量关系的是C;
分析:由题意可知:每户每月用水量不超过6吨,每吨价格为2.5元;即6吨以内,每吨水的单价变化不大,然后水量超过6吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即可。
故选:C
6.下列统计图中的( ),能反映热水冷却过程中温度的变化情况.
A. B.
C. D.
答案:C
解答:解:反映热水冷却过程中温度的变化情况,温度慢慢降低,降到0度后,温度不变,
所以能反映热水冷却过程中温度的变化情况的是C。
分析:根据生活经验可知:反映热水冷却过程中温度的变化情况,温度慢慢降低,降到0度后,温度不变;由此选择即可。
故选:C
7.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5千米远的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校.下面四幅图中,描述了育才小学六年级同学这一活动行程的是图( )
A. B. C. D.
答案:A
解答:解:折线统计图A所提供的信息与题中所提供的信息相同;
分析:由折线统计图:A所提供的信息是从学校出发,乘车0.5小时,来到离校5千米的科技馆,参观1小时返回学校;
折线统计图B提供的信息是从学校出发去科技馆,在科技馆玩了1.5小时后乘车回学校;
折线统计图C提供的信息在返回的时间为2.5﹣1.5=1时,与题干不符合;
折线统计图D是从科技馆出发乘车1小时,来到离科技馆5千米的学校,参观1小时返回科技馆,据此解答。
故选:A
8.小红从家出发去商店买新年联欢会用品,当她走了大约一半路程时想起忘了带钱.于是她回家取钱,然后再返回,买了东西后就回家了.下面( )幅图比较准确地反映了小红的行为.
A. B. C.
答案:C
解答:解:符合小红这段时间离家距离变化的是C。
分析:离家的距离是随时间是这样变化的:
(1)先离家越来远,到了最远距离一半的时候;
(2)然后越来越近直到为0;
(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;
(4)然后再离家越来越远,直到商店;
(5)在商店买书还要一段时间,所以离家最远的时候也是一条线段;
(6)然后回家直到离家的距离为0。
故选:C
9.宁宁从家出发去少年宫听讲座,当他走了大约一半路程时,想起忘了带门票.于是他回家取票,然后再去少年宫,听完报告后回家.下面( )幅图比较准确地反映了宁宁的行为.
A. B. C.
答案:C
解答:解:符合宁宁这段时间离家距离变化的是C。
分析:离家的距离是随时间是这样变化的:
(1)先离家越来远,到了最远距离一半的时候;
(2)然后越来越近直到为0;
(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;
(4)然后再离家越来越远,直到少年宫;
(5)在少年宫听报告还要一段时间,所以离家最远的时候也是一条线段;
(6)然后回家直到离家的距离为0。
故选:C
10.劳义早晨离开训练地跑了30分,然后回到训练地喝水,又跑了30分后休息15分,再回到训练.下图( )比较准确的反映了他的行为.
A. B. C.
答案:B
解答:解:符合劳义这段时间离训练地距离变化的是B。
分析:离训练地的距离是随时间是这样变化的:
(1)先离训练地越来远,到了最远距离的时候;
(2)然后又回到训练地喝水,即与训练地的距离越来越近直到为0;
(3)到训练地喝水有一段时间,所以有一段时间离家的距离为0;
(4)然后再离训练地越来越远,直到达第一次的距离;
(5)在第一返回的距离,休息15分钟,所以此时的折线是持平的;
(6)休息后再返回训练地的距离为0。
故选:B
11.某市规定每户用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨水价为3元.下图能表示每月水费与用水量关系的示意图是( )
A. B.
C. D.
答案:C
解答:解:由解析知:每户每月用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨价格为3元.下面4幅图中能表示每月水费与用水量关系的是C;
分析:由题意可知:每户每月用水量不超过10吨,每吨价格为2.5元;即10吨以内,每吨水的单价变化不大,然后水量超过10吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即。
故选:C
12.六(l)班班长统计去年1﹣8月“书香校园”活动中全班同学的课外阅数量(单位:本)绘制了如下的折线统计图,下列说法正确的是( )
A. 平均数是58本
B. 众数是42本
C. 中位数是58木
D. 每月阅读数量超过40本的有5个月
答案:C
解答:解:平均数:(36+70+58+42+58+28+75+83)÷8
=450÷8,
=56.52,
按照从小到大的顺序排列为:28,36,42,58,58,70,75,83,
中位数为:(58+58)÷2=58,
答:这组数据的平均数是56.52,中位数是58。
分析:A、把这组数据的所有数相加的和再除以8进行计算后再判断即可;
B、在一组数据中,出现次数最多的数叫做这组数据的众数,42在本组数据中只出现了1次,58出现了2次,出现的次数最多,所有58是这组数据的众数,故排除;
C、把这组数据按照从小到大的顺序排列,排在中间位置上两个数的平均数即是这组数据的中位数;
D、每个月阅读数量超过40本的有6个月,故排除。
故选:C
13.反映一位病人24小时内心跳次数的变化情况,护士需要把病人心跳数据制成( )
A. 统计表 B. 条形统计图 C. 折线统计图
答案:C
解答:解:折线统计图不仅可以表示数量的多少,而且可以反映同一事物在不同时间里的发展变化的情况,
所以反映一位病人24小时内心跳的次数的变化情况,把病人的心跳数据制成折线统计图最合适。
分析:以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图,与条形统计图、统计表相比较,折线统计图不仅可以表示数量的多少,而且可以反映同一事物在不同时间里的发展变化的情况,所以反映一位病人24小时内心跳的次数的变化情况,把病人的心跳数据制成折线统计图最合适。
故选:C
14.如图所示的图象表示斑马和长颈鹿的奔跑情况,下面的说法不符合这个图象的是( )
A. 斑马奔跑的路程与奔跑的时间成比例
B. 长颈鹿25分钟跑了20千米
C. 长颈鹿比斑马跑得快
D. 斑马跑12千米用了10分钟
答案:C
解答:解:A、因为12÷10=1.2千米,24÷20=1.2千米,…,即斑马奔跑的路程÷奔跑的时间=斑马速度(一定),所以奔跑的路程与奔跑的时间成正比例;
B、由图象可知:长颈鹿25分钟跑了20千米;
C、由图象可知:斑马比长颈鹿跑的快,所以C选项长颈鹿比斑马跑得快,说法错误;
D、由图象可知:斑马跑12千米用了10分钟;
分析:根据图象对各选项进行依次解析、进而得出结论。
故选:C
15.陈老师上午要上三节课.第一节课到三楼给四(1)班同学上数学课,第二节课到二楼给三(1)班同学上美术课,第三节课到四楼给五(1)班同学上数学课,上完三节课后才回到一楼办公室.下面哪一幅图比较准确地描述了这件事?( )
A. B. C.
答案:B
解答:解:A、第一节课在三楼和第三节课的四楼等高,不符合题意;
B、第一节课到三楼,较高;第二节课到二楼,下降一层;第三节课到四楼,最高;第四节课到一楼,回到起点;符合题意;
C、第二节课在二楼比第一节课所在的三楼还高,不符合题意;
分析:根据题意,为了描述这件事,画折线图,横轴为时间,纵轴为楼层,爬楼时,随时间高度在变大,下楼时高度变小,停留在楼上上课时,高度不变,即与横轴平行,不同的楼层,高度不同,体现在图上纵轴的数据大小不同.由此逐个解析,即可得解。
故选:B
二、填空题(共5小题)
16.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况. .(判断对错)
答案:√
解答:解:折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
故答案为:√
分析:分析:根据折线统计图的特点,折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
17.甲、乙两车分别从A、B两地同时出发,它们距A地的距离S与行驶时间t的关系如图所示,根据图象可知,甲车从B地返回的速度为 千米/小时,甲车行驶到距A地 千米时追上乙车.
答案:80,40
解答:解:A、B两地之间的路程是120千米,甲车返回用1.5小时,
甲返回的速度是:120÷1.5=80(千米/小时);
乙车的速度是:120÷3=40(千米/小时);
甲从B地返回追上乙用的时间:
40÷(80﹣40)
=40÷40
=1(小时);
也就是甲车离开B地80千米,那么距A地120﹣80=40千米.
答:甲车返回的速度是80千米/小时,甲车行驶到距A地40千米时追上乙车.
故答案为:80,40。
分析:根据图象可知:A、B两地之间的路程是120千米,根据速度=路程÷时间,甲车返回用1.5小时,据此可以求出甲返回的速度,乙车用行完全程用3小时,由此可以求出乙车的速度,当甲车达到B地时,乙车离开B地1小时的路程,根据追及问题:追及时间=追及的距离÷速度差,由此可以求出甲追上乙所用的时间,进而求出甲车行驶到距A地多少千米时追上乙车.据此解答。
18.如图的图象表示斑马和长颈鹿的奔跑情况.
(1)斑马的奔跑路程和奔跑时间成 比例.
(2)长颈鹿18分钟跑了 千米.
答案:正;14.4
解答:解:(1)根据图象可知,长颈鹿奔跑的速度是一定的,即路程和时间的比值一定,所以路程和时间成正比例关系;
(2)4÷5×18
=0.8×18
=14.4(千米)
答:长颈鹿18分钟跑了14.4千米.
故答案为:正;14.4。
分析:(1)斑马奔跑的速度是一定的,即路程和时间的比值一定,所以路程和时间成正比例关系;
(2)依据图象可知,长颈鹿5分钟跑了4千米,根据路程÷时间=速度,再根据速度×时间=路程,据此解答。
19.哥哥和弟弟周末骑车去森林动物园游玩,途中骑行情况如图.哥哥骑行的路程和时间成 比例,弟弟每分钟行 千米.
答案:正,0.16
解答:解:因为路程=速度×时间,
所以哥哥骑车行驶的路程与时间成正比例,
8时15分﹣7时=75(分钟),
12÷75=0.16(千米);
答:哥哥骑车行驶的路程与时间成正比例,弟弟骑车每分钟行0.16千米.
故答案为:正,0.16。
分析:此题是行程问题中的数量关系,根据成正比例的意义可知,行驶的路程与时间成正比例关系;
通过观察统计图可得出弟弟行驶的路程为12千米,时间为8时15分﹣7时=75分钟,根据速度=路程÷时间即可解决问题。
20.小华从家去相距5千米远的图书馆借书,经过情况如右图.
(1)小华在图书馆借书用了 小时.
(2)返回的速度是每小时 千米.
答案:1,5
解答:解:(1)2.5﹣1.5=1(小时);
(2)5÷(3.5﹣2.5)
=5÷1
=5(千米/时);
答:小华在图书馆借书用了 1小时;返回的速度是每小时5千米;
故答案为:1,5
分析:根据统计图可知,小华从家到图书馆一共用了1.5小时,其中在路上休息了0.5小时,实际用了1小时;在图书馆借书用了1小时;返回用了1小时,由此列式解答。
三.解答题(共5小题)
21.下面是航模小组制作的两架航模飞机在一次飞行中飞行时间和高度的记录.
(1)甲飞机飞行 秒,乙飞机飞行 秒,甲飞机的飞行时间比乙飞机长.
(2)从图上看,起飞后第10秒乙飞机的高度是 米,起飞后第 秒两架飞机处于同一高度,起飞后大约 秒两架飞机的高度相差最大.
(3)说说从起飞后第15秒至20秒乙飞机的飞行状态. .
答案:40,35,| 20,15,30|匀速飞行
解答:解:(1)(40﹣35)÷35=
答:甲飞机飞行40秒,乙飞机飞行35秒,甲飞机的飞行时间比乙飞机长.
(2)从图上看,起飞后第10秒乙飞机的高度是20米,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大.
(3)从起飞后第15秒至20秒乙飞机的飞行状态是匀速飞行。
分析:(1)根据图意进行解答,用甲飞机飞行的时间减去乙飞机飞行的时间,再除以乙飞机飞行的时间。
(2)从图上看,起飞后第10秒乙飞机的高度是20米,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大.
(3)飞机的速度不变,所以是匀速飞行。
22.如图是甲、乙二人步行情况的统计图.看图回答下列问题:
(1)乙比甲晚出发 分钟.
(2)甲在途中休息了 分钟.
(3)乙是在距出发地 米的地方追上甲的.
(4)乙散步的平均速度是每分钟 米.
答案:4,4,300,35
解答:解:由统计图可知:
(1)乙比甲晚出发4分钟;
(2)甲在途中休息了4分钟;
(3)乙是在距出发地300米的地方追上甲的;
(4)350÷(14﹣4)
=350÷10
=35(米);
答:乙散步的平均速度是每分钟35米。
故答案为:4,4,300,35.
分析:由统计图可知:
(1)乙比甲晚出发4分钟;
(2)甲在途中休息了4分钟;
(3)乙是在距出发地300米的地方追上甲的;
(4)根据速度=路程除以时间,即可解答。
23.下面是张兰四年级下期五次数学测试的成绩:
次数 第一次 第二次 第三次 第四次 第五次
成绩/分 75 83 80 95 97
(1)根据表中数据,绘制折线统计图.
(2)第 次到第 次成绩上升最快.
(3)张兰四年级下期数学成绩整体趋势是 .
(4)请你预测,张兰第六次数学测试可能会得 分.
答案:
如图:
三,四,逐步上升,100
解答:解:(1)根据表中数据,绘制折线统计图.
(2)第三次到第四次成绩上升最快;
(3)张兰四年级下期数学成绩整体趋势是逐步上升.
(4)请你预测,张兰第六次数学测试可能会得100分.
故答案为:三,四,逐步上升,100。
分析:(1)根据表中的数据,进行找点、描点、连线即可绘制成折线统计图;
(2)由图可知:第三次到第四次成绩上升最快;
(3)因为张兰四年级下期数学成绩变化为:75→83→80→95→97,则成绩整体趋势是逐步上升.
(4)根据成绩变化进行预测,张兰第六次数学测试可能会得100分。
24.下面是五(3)班小军(男)和小娟(女)6﹣12岁的身高统计图,看图回答问题.
(1)9岁时,小军比小娟高 厘米.
(2) 岁时,小军和小娟一样高.
(3) 岁时,小军比小娟矮3厘米.
(4)小娟从6﹣12岁身高每年平均增长多少 厘米?
答案:2、10、12、5.83
解答:解:(1)9岁时,小军比小娟高 2厘米.
(2)10岁时,小军和小娟一样高.
(3)12岁时,小军比小娟矮3厘米.
(4)[(122﹣117)+(126﹣122)+(132﹣126)+(138﹣132)+(144﹣138)+(150﹣144)]÷6
=[5+6+6+6+6+6]÷6
=35÷6
≈5.83(厘米)
答:小娟从6﹣12岁身高每年平均增长多少 5.83厘米.
故答案为:2、10、12、5.83
分析:(1)(2)(3)观察统计图即可得出相关的数据,直接进行解答即可;
(4)先计算出小娟从6﹣12岁每年身高增长的和,再除以6即可得解。
25.请根据下面的统计图回答下列问题.
(1) 月份收入和支出相差最小.
(2)9月份收入和支出相差 万元.
(3)全年实际收入 万元.
(4)平均每月支出 万元.
(5)你还获得了哪些信息?
答案: 4|30|740|30。
解答:解:(1)由图示得出:4月份收入和支出相差最小;
(2)70﹣40=30(万元).
答:9月份收入和支出相差30万元.
(3)40+60+30+30+50+60+80+70+70+80+90+80=740(万元).
答:全年实际收入740万元.
(4)(20+30+10+20+20+30+20+30+40+50+40+50)÷12=360÷12=30(万元).
答:平均每月支出30万元.
(5)得出:7月份收入和支出相差最大.
故答案为:(1)4;(2)30;(3)740;(4)30。
分析:(1)同一个月份收入和支出的点最接近的相差最小;
(2)用9月份收入减支出即可;
(3)把12个月的收入相加即可;
(4)用12个月的总支出除以12即可;
(5)从图中获得正确信息即可。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新人教版数学五年级下册第七章7.1折线统计图课时练习
一、选择题(共15小题)
1.在常见的折线统计图上,表示( )
A. 不变 B. 缓慢上升 C. 缓慢下降 D. 大幅上升
答案:B
解答:解:在常见的折线统计图上,表示缓慢上升;
分析:折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;如图所示的情况,属于缓慢上升,据此解答即可。
故选:B
2.从家去图书馆,中途休息了几分钟,借完书后直接回家.能描述这一过程图象的是( )
A. B.
C. D.
答案:A
解答:解:小红的这一过程可分成以下几段:
(1)从家出发到途中休息前,这一段时间里离家的距离越来越远;
(2)途中休息,这一段时间离家的距离不变;
(3)途中休息后到图书馆,这一段时间里离家的距离越来越远;
(4)在图书馆借书,这一段时间离家的距离不变;
(5)从图书馆回家,这一段时间里离家的距离越来越近。
只有选项A符合这一变化。
分析:根据所给的条件,解析出时间与离家距离之间的关系,再从选项中找出符合的答案。
故选:A
3.李老师骑车外出办事,离学校不久便接到学校要他返校的紧急电话,李老师急忙赶回学校,下面四个图象中,描述李老师与学校距离的图象是( )
A. B.
C. D.
答案:C
解答:解:李老师从学校出发离校,接到电话前,距离是随着时间的增加而增加的,接到电话后,开始返校,距离是随着时间的增加而减少的,故A、B、D不符合题意,又因返回时与来时同样的距离相等,所以返回时用的时间与来时差不多,所以C正确。
分析:根据题意可知没有接到电话前,距离是增加的,接到电话后距离开始减少,直至到学校即距离为0,据此解答。
故选:C
4.如图:向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致是下列图象中的( )
A. B.
C. D.
答案:B
解答:解:如图,
向放在水槽底部的烧杯注水(流量一定)注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度与注水时间之间的关系大致图象是:
;
分析:本题中的时间可分为三个段.第一段从注水开始到水注满烧杯结束,在这段时间内水槽的水面高度为零;第二段时间从水槽内有水开始到高度上升到烧杯的高度为止,在这段时间内水槽内水的高度迅速增加;第三段时间从水到烧杯高度开始到水槽内的水注满结束,在这段时间内水槽内的水的高度缓慢增加.所以在图象上表示为第一段时间内高度为零,由于第三段时间内水高上升的速度要比第二段时间内上升的缓慢,在图象上表示为第三部分要比第二部分平缓,所以应选择B答案。
故选:B
5.某市规定每户每月用水量不超过6吨时,每吨价格2.5元;当用水量超过6吨时,超过部分每吨价格3元.下图中能正确表示每月水费与用水量关系的示意图是( )
A. B. C. D.
答案:C
解答:解:由解析知:每户每月用水量不超过6吨,每吨价格为2.5元;当用水量超过6吨时,超过部分每吨价格为3元.下面3幅图中能表示每月水费与用水量关系的是C;
分析:由题意可知:每户每月用水量不超过6吨,每吨价格为2.5元;即6吨以内,每吨水的单价变化不大,然后水量超过6吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即可。
故选:C
6.下列统计图中的( ),能反映热水冷却过程中温度的变化情况.
A. B.
C. D.
答案:C
解答:解:反映热水冷却过程中温度的变化情况,温度慢慢降低,降到0度后,温度不变,
所以能反映热水冷却过程中温度的变化情况的是C。
分析:根据生活经验可知:反映热水冷却过程中温度的变化情况,温度慢慢降低,降到0度后,温度不变;由此选择即可。
故选:C
7.育才小学六年级同学从学校出发,乘车0.5时,来到离学校5千米远的科技馆,参观1时,出馆后休息0.5时,然后乘车0.5时返回学校.下面四幅图中,描述了育才小学六年级同学这一活动行程的是图( )
A. B. C. D.
答案:A
解答:解:折线统计图A所提供的信息与题中所提供的信息相同;
分析:由折线统计图:A所提供的信息是从学校出发,乘车0.5小时,来到离校5千米的科技馆,参观1小时返回学校;
折线统计图B提供的信息是从学校出发去科技馆,在科技馆玩了1.5小时后乘车回学校;
折线统计图C提供的信息在返回的时间为2.5﹣1.5=1时,与题干不符合;
折线统计图D是从科技馆出发乘车1小时,来到离科技馆5千米的学校,参观1小时返回科技馆,据此解答。
故选:A
8.小红从家出发去商店买新年联欢会用品,当她走了大约一半路程时想起忘了带钱.于是她回家取钱,然后再返回,买了东西后就回家了.下面( )幅图比较准确地反映了小红的行为.
A. B. C.
答案:C
解答:解:符合小红这段时间离家距离变化的是C。
分析:离家的距离是随时间是这样变化的:
(1)先离家越来远,到了最远距离一半的时候;
(2)然后越来越近直到为0;
(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;
(4)然后再离家越来越远,直到商店;
(5)在商店买书还要一段时间,所以离家最远的时候也是一条线段;
(6)然后回家直到离家的距离为0。
故选:C
9.宁宁从家出发去少年宫听讲座,当他走了大约一半路程时,想起忘了带门票.于是他回家取票,然后再去少年宫,听完报告后回家.下面( )幅图比较准确地反映了宁宁的行为.
A. B. C.
答案:C
解答:解:符合宁宁这段时间离家距离变化的是C。
分析:离家的距离是随时间是这样变化的:
(1)先离家越来远,到了最远距离一半的时候;
(2)然后越来越近直到为0;
(3)到家拿钱有一段时间,所以有一段时间离家的距离为0;
(4)然后再离家越来越远,直到少年宫;
(5)在少年宫听报告还要一段时间,所以离家最远的时候也是一条线段;
(6)然后回家直到离家的距离为0。
故选:C
10.劳义早晨离开训练地跑了30分,然后回到训练地喝水,又跑了30分后休息15分,再回到训练.下图( )比较准确的反映了他的行为.
A. B. C.
答案:B
解答:解:符合劳义这段时间离训练地距离变化的是B。
分析:离训练地的距离是随时间是这样变化的:
(1)先离训练地越来远,到了最远距离的时候;
(2)然后又回到训练地喝水,即与训练地的距离越来越近直到为0;
(3)到训练地喝水有一段时间,所以有一段时间离家的距离为0;
(4)然后再离训练地越来越远,直到达第一次的距离;
(5)在第一返回的距离,休息15分钟,所以此时的折线是持平的;
(6)休息后再返回训练地的距离为0。
故选:B
11.某市规定每户用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨水价为3元.下图能表示每月水费与用水量关系的示意图是( )
A. B.
C. D.
答案:C
解答:解:由解析知:每户每月用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨价格为3元.下面4幅图中能表示每月水费与用水量关系的是C;
分析:由题意可知:每户每月用水量不超过10吨,每吨价格为2.5元;即10吨以内,每吨水的单价变化不大,然后水量超过10吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即。
故选:C
12.六(l)班班长统计去年1﹣8月“书香校园”活动中全班同学的课外阅数量(单位:本)绘制了如下的折线统计图,下列说法正确的是( )
A. 平均数是58本
B. 众数是42本
C. 中位数是58木
D. 每月阅读数量超过40本的有5个月
答案:C
解答:解:平均数:(36+70+58+42+58+28+75+83)÷8
=450÷8,
=56.52,
按照从小到大的顺序排列为:28,36,42,58,58,70,75,83,
中位数为:(58+58)÷2=58,
答:这组数据的平均数是56.52,中位数是58。
分析:A、把这组数据的所有数相加的和再除以8进行计算后再判断即可;
B、在一组数据中,出现次数最多的数叫做这组数据的众数,42在本组数据中只出现了1次,58出现了2次,出现的次数最多,所有58是这组数据的众数,故排除;
C、把这组数据按照从小到大的顺序排列,排在中间位置上两个数的平均数即是这组数据的中位数;
D、每个月阅读数量超过40本的有6个月,故排除。
故选:C
13.反映一位病人24小时内心跳次数的变化情况,护士需要把病人心跳数据制成( )
A. 统计表 B. 条形统计图 C. 折线统计图
答案:C
解答:解:折线统计图不仅可以表示数量的多少,而且可以反映同一事物在不同时间里的发展变化的情况,
所以反映一位病人24小时内心跳的次数的变化情况,把病人的心跳数据制成折线统计图最合适。
分析:以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图,与条形统计图、统计表相比较,折线统计图不仅可以表示数量的多少,而且可以反映同一事物在不同时间里的发展变化的情况,所以反映一位病人24小时内心跳的次数的变化情况,把病人的心跳数据制成折线统计图最合适。
故选:C
14.如图所示的图象表示斑马和长颈鹿的奔跑情况,下面的说法不符合这个图象的是( )
A. 斑马奔跑的路程与奔跑的时间成比例
B. 长颈鹿25分钟跑了20千米
C. 长颈鹿比斑马跑得快
D. 斑马跑12千米用了10分钟
答案:C
解答:解:A、因为12÷10=1.2千米,24÷20=1.2千米,…,即斑马奔跑的路程÷奔跑的时间=斑马速度(一定),所以奔跑的路程与奔跑的时间成正比例;
B、由图象可知:长颈鹿25分钟跑了20千米;
C、由图象可知:斑马比长颈鹿跑的快,所以C选项长颈鹿比斑马跑得快,说法错误;
D、由图象可知:斑马跑12千米用了10分钟;
分析:根据图象对各选项进行依次解析、进而得出结论。
故选:C
15.陈老师上午要上三节课.第一节课到三楼给四(1)班同学上数学课,第二节课到二楼给三(1)班同学上美术课,第三节课到四楼给五(1)班同学上数学课,上完三节课后才回到一楼办公室.下面哪一幅图比较准确地描述了这件事?( )
A. B. C.
答案:B
解答:解:A、第一节课在三楼和第三节课的四楼等高,不符合题意;
B、第一节课到三楼,较高;第二节课到二楼,下降一层;第三节课到四楼,最高;第四节课到一楼,回到起点;符合题意;
C、第二节课在二楼比第一节课所在的三楼还高,不符合题意;
分析:根据题意,为了描述这件事,画折线图,横轴为时间,纵轴为楼层,爬楼时,随时间高度在变大,下楼时高度变小,停留在楼上上课时,高度不变,即与横轴平行,不同的楼层,高度不同,体现在图上纵轴的数据大小不同.由此逐个解析,即可得解。
故选:B
二、填空题(共5小题)
16.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况. .(判断对错)
答案:√
解答:解:折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
故答案为:√
分析:分析:根据折线统计图的特点,折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
17.甲、乙两车分别从A、B两地同时出发,它们距A地的距离S与行驶时间t的关系如图所示,根据图象可知,甲车从B地返回的速度为 千米/小时,甲车行驶到距A地 千米时追上乙车.
答案:80,40
解答:解:A、B两地之间的路程是120千米,甲车返回用1.5小时,
甲返回的速度是:120÷1.5=80(千米/小时);
乙车的速度是:120÷3=40(千米/小时);
甲从B地返回追上乙用的时间:
40÷(80﹣40)
=40÷40
=1(小时);
也就是甲车离开B地80千米,那么距A地120﹣80=40千米.
答:甲车返回的速度是80千米/小时,甲车行驶到距A地40千米时追上乙车.
故答案为:80,40。
分析:根据图象可知:A、B两地之间的路程是120千米,根据速度=路程÷时间,甲车返回用1.5小时,据此可以求出甲返回的速度,乙车用行完全程用3小时,由此可以求出乙车的速度,当甲车达到B地时,乙车离开B地1小时的路程,根据追及问题:追及时间=追及的距离÷速度差,由此可以求出甲追上乙所用的时间,进而求出甲车行驶到距A地多少千米时追上乙车.据此解答。
18.如图的图象表示斑马和长颈鹿的奔跑情况.
(1)斑马的奔跑路程和奔跑时间成 比例.
(2)长颈鹿18分钟跑了 千米.
答案:正;14.4
解答:解:(1)根据图象可知,长颈鹿奔跑的速度是一定的,即路程和时间的比值一定,所以路程和时间成正比例关系;
(2)4÷5×18
=0.8×18
=14.4(千米)
答:长颈鹿18分钟跑了14.4千米.
故答案为:正;14.4。
分析:(1)斑马奔跑的速度是一定的,即路程和时间的比值一定,所以路程和时间成正比例关系;
(2)依据图象可知,长颈鹿5分钟跑了4千米,根据路程÷时间=速度,再根据速度×时间=路程,据此解答。
19.哥哥和弟弟周末骑车去森林动物园游玩,途中骑行情况如图.哥哥骑行的路程和时间成 比例,弟弟每分钟行 千米.
答案:正,0.16
解答:解:因为路程=速度×时间,
所以哥哥骑车行驶的路程与时间成正比例,
8时15分﹣7时=75(分钟),
12÷75=0.16(千米);
答:哥哥骑车行驶的路程与时间成正比例,弟弟骑车每分钟行0.16千米.
故答案为:正,0.16。
分析:此题是行程问题中的数量关系,根据成正比例的意义可知,行驶的路程与时间成正比例关系;
通过观察统计图可得出弟弟行驶的路程为12千米,时间为8时15分﹣7时=75分钟,根据速度=路程÷时间即可解决问题。
20.小华从家去相距5千米远的图书馆借书,经过情况如右图.
(1)小华在图书馆借书用了 小时.
(2)返回的速度是每小时 千米.
答案:1,5
解答:解:(1)2.5﹣1.5=1(小时);
(2)5÷(3.5﹣2.5)
=5÷1
=5(千米/时);
答:小华在图书馆借书用了 1小时;返回的速度是每小时5千米;
故答案为:1,5
分析:根据统计图可知,小华从家到图书馆一共用了1.5小时,其中在路上休息了0.5小时,实际用了1小时;在图书馆借书用了1小时;返回用了1小时,由此列式解答。
三.解答题(共5小题)
21.下面是航模小组制作的两架航模飞机在一次飞行中飞行时间和高度的记录.
(1)甲飞机飞行 秒,乙飞机飞行 秒,甲飞机的飞行时间比乙飞机长.
(2)从图上看,起飞后第10秒乙飞机的高度是 米,起飞后第 秒两架飞机处于同一高度,起飞后大约 秒两架飞机的高度相差最大.
(3)说说从起飞后第15秒至20秒乙飞机的飞行状态. .
答案:40,35,| 20,15,30|匀速飞行
解答:解:(1)(40﹣35)÷35=
答:甲飞机飞行40秒,乙飞机飞行35秒,甲飞机的飞行时间比乙飞机长.
(2)从图上看,起飞后第10秒乙飞机的高度是20米,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大.
(3)从起飞后第15秒至20秒乙飞机的飞行状态是匀速飞行。
分析:(1)根据图意进行解答,用甲飞机飞行的时间减去乙飞机飞行的时间,再除以乙飞机飞行的时间。
(2)从图上看,起飞后第10秒乙飞机的高度是20米,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大.
(3)飞机的速度不变,所以是匀速飞行。
22.如图是甲、乙二人步行情况的统计图.看图回答下列问题:
(1)乙比甲晚出发 分钟.
(2)甲在途中休息了 分钟.
(3)乙是在距出发地 米的地方追上甲的.
(4)乙散步的平均速度是每分钟 米.
答案:4,4,300,35
解答:解:由统计图可知:
(1)乙比甲晚出发4分钟;
(2)甲在途中休息了4分钟;
(3)乙是在距出发地300米的地方追上甲的;
(4)350÷(14﹣4)
=350÷10
=35(米);
答:乙散步的平均速度是每分钟35米。
故答案为:4,4,300,35.
分析:由统计图可知:
(1)乙比甲晚出发4分钟;
(2)甲在途中休息了4分钟;
(3)乙是在距出发地300米的地方追上甲的;
(4)根据速度=路程除以时间,即可解答。
23.下面是张兰四年级下期五次数学测试的成绩:
次数 第一次 第二次 第三次 第四次 第五次
成绩/分 75 83 80 95 97
(1)根据表中数据,绘制折线统计图.
(2)第 次到第 次成绩上升最快.
(3)张兰四年级下期数学成绩整体趋势是 .
(4)请你预测,张兰第六次数学测试可能会得 分.
答案:
如图:
三,四,逐步上升,100
解答:解:(1)根据表中数据,绘制折线统计图.
(2)第三次到第四次成绩上升最快;
(3)张兰四年级下期数学成绩整体趋势是逐步上升.
(4)请你预测,张兰第六次数学测试可能会得100分.
故答案为:三,四,逐步上升,100。
分析:(1)根据表中的数据,进行找点、描点、连线即可绘制成折线统计图;
(2)由图可知:第三次到第四次成绩上升最快;
(3)因为张兰四年级下期数学成绩变化为:75→83→80→95→97,则成绩整体趋势是逐步上升.
(4)根据成绩变化进行预测,张兰第六次数学测试可能会得100分。
24.下面是五(3)班小军(男)和小娟(女)6﹣12岁的身高统计图,看图回答问题.
(1)9岁时,小军比小娟高 厘米.
(2) 岁时,小军和小娟一样高.
(3) 岁时,小军比小娟矮3厘米.
(4)小娟从6﹣12岁身高每年平均增长多少 厘米?
答案:2、10、12、5.83
解答:解:(1)9岁时,小军比小娟高 2厘米.
(2)10岁时,小军和小娟一样高.
(3)12岁时,小军比小娟矮3厘米.
(4)[(122﹣117)+(126﹣122)+(132﹣126)+(138﹣132)+(144﹣138)+(150﹣144)]÷6
=[5+6+6+6+6+6]÷6
=35÷6
≈5.83(厘米)
答:小娟从6﹣12岁身高每年平均增长多少 5.83厘米.
故答案为:2、10、12、5.83
分析:(1)(2)(3)观察统计图即可得出相关的数据,直接进行解答即可;
(4)先计算出小娟从6﹣12岁每年身高增长的和,再除以6即可得解。
25.请根据下面的统计图回答下列问题.
(1) 月份收入和支出相差最小.
(2)9月份收入和支出相差 万元.
(3)全年实际收入 万元.
(4)平均每月支出 万元.
(5)你还获得了哪些信息?
答案: 4|30|740|30。
解答:解:(1)由图示得出:4月份收入和支出相差最小;
(2)70﹣40=30(万元).
答:9月份收入和支出相差30万元.
(3)40+60+30+30+50+60+80+70+70+80+90+80=740(万元).
答:全年实际收入740万元.
(4)(20+30+10+20+20+30+20+30+40+50+40+50)÷12=360÷12=30(万元).
答:平均每月支出30万元.
(5)得出:7月份收入和支出相差最大.
故答案为:(1)4;(2)30;(3)740;(4)30。
分析:(1)同一个月份收入和支出的点最接近的相差最小;
(2)用9月份收入减支出即可;
(3)把12个月的收入相加即可;
(4)用12个月的总支出除以12即可;
(5)从图中获得正确信息即可。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
