北京市门头沟中学2025年中考数学二轮复习 专题一 基础夯实·任务1 实数及其运算 课件(共25张PPT)
文档属性
| 名称 | 北京市门头沟中学2025年中考数学二轮复习 专题一 基础夯实·任务1 实数及其运算 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
2025年数学中考复习
专题一 基础夯实
任务1 实数及其运算
知识点1 实数的分类
1.按定义分
2.按正负分
知识点2 实数的相关概念
名称 定义 性质
数轴 规定了 ①______、②________ 和③__________的直线 叫作数轴 (1)数轴上两个点表示的数,右边的
总比左边的④____;(2)数轴上的点
与实数具有⑤__________的关系;
(3)数轴上位于原点两侧,到原点距
离相等的点表示的数⑥____________,
这两个数的⑦________相等
原点
正方向
单位长度
大
一一对应
互为相反数
绝对值
名称 定义 性质
相反数 只有⑧______不同的两 个数互为相反数 (1)互为相反数的两个数, 表示:
____; ___;
(2)0的相反数是 ___
倒数 如果两个数的 _______ ___,那么称这两个数互 为倒数 (1) ___没有倒数;(2)一个非零
数 的倒数为 _ _
符号
0
0
乘积为1
0
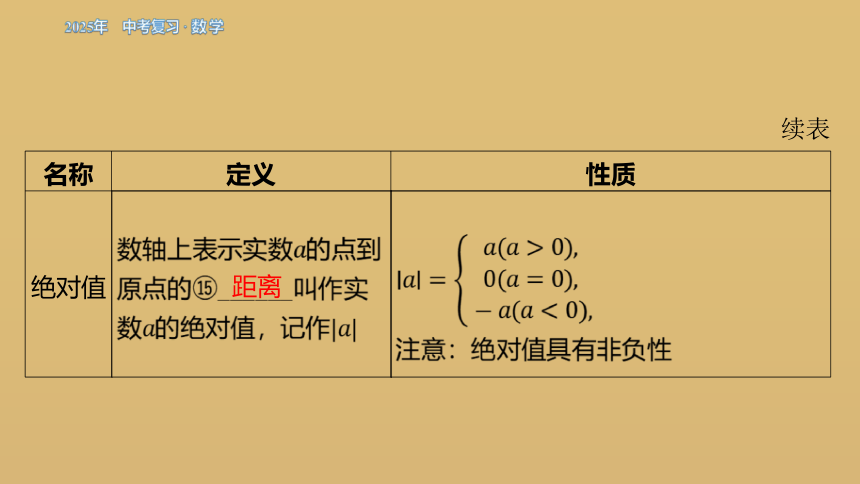
续表
名称 定义 性质
绝对值 数轴上表示实数 的点到 原点的 ______叫作实 数的绝对值,记作
注意:绝对值具有非负性
距离
续表
知识点3 实数的大小比较
1.数轴上两个点表示的数,右边的总比左边的____。
2.正数大于0,负数小于0,正数大于一切负数,两个负数中绝对值大
的反而____。
大
小
知识点4 科学记数法
1.科学记数法的表示形式:________。
和 的确定
(1)的确定:是整数位只有一位的数,即 。
(2)的确定:当一个数的绝对值大于10时, 是正整数,其值等于
原数的整数位数_____,或等于原数变为 时,小数点向左移动的位数;当
一个数的绝对值小于1时,是负整数, 的绝对值等于原数左起第一个非
零数字前______________(包括______________),或等于原数变为 时,
小数点向右移动的位数。
减1
所有零的个数
小数点前的零
知识点5 平方根、算术平方根和立方根
1.平方根、算术平方根和立方根
名称 含义 表示 性质
平方 根 如果一个数 的平 方等于 ,那么这个 数叫作 的 ①________ 实数 的 平方根表示 为②_____ (1)一个正数有两个平方根,它
们③____________;0的平方根是
④___;负数没有平方根;
(2)平方根等于它本身的数是⑤
___
平方根
互为相反数
0
0
名称 含义 表示 性质
算术 平方 根 如果一个正数 的 平方等于 ,那么这 个正数叫作 的⑥ ____________ 实数 的 算术平方根 表示为 ⑦____ (1)一个正数有一个正的算术平
方根(双重非负性);0的算术平
方根是⑧___;负数没有算术平方
根;
(2)算术平方根等于它本身的数
是⑨______
算术平方根
0
0和1
续表
名称 含义 表示 性质
立方 根 如果一个数 的立 方等于 ,那么这个 数叫作 的 ⑩________ 实数 的立 方根表示为 ____ (1)所有的数都有一个立方根,
且与原数同号;
(2)立方根等于它本身的数是
_______
立方根
0和
续表
2.开方
(1)求一个数的平方根的运算,叫作开平方,其中 叫作被开方数;
(2)求一个数的立方根的运算,叫作开立方,其中 叫作被开方数。
知识点6 实数的运算
1.加法:(1)同号两数相加,取相同的符号,并把____________;
(2)异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对
值较大的加数的符号,并用较大的绝对值______较小的绝对值。
2.减法:减去一个数,等于加上这个数的________,即
______。
3.乘法:两数相乘,同号得正,异号得负,并把绝对值相乘,即
, 。(注意:任何数与0相乘,积仍为0)
绝对值相加
减去
相反数
4.除法:除以一个不等于0的数,等于乘这个数的倒数,即
__ 。(注意:0除以任何不等于0的数,仍得0)
5.乘方:,表示个 相乘。
(注意:,表示个 相加)
6.实数混合运算的运算顺序:先算乘方,再算乘除,最后算加减,有
括号的先算括号里面的;同级运算要按照从左到右的顺序依次进行。
任务二 整式及因式分解
知识点1 整式的相关概念
1.代数式:用运算符号把数和字母连接而成的式子。
2.单项式:(1)定义:由数或字母的积所组成的代数式叫作单项式。
(单独一个数或字母也是单项式)
(2)系数:单项式中的__________。
(3)次数:单项式中__________指数的和。
3.多项式:(1)定义:几个单项式的和叫作多项式。
(2)项:多项式中的每个________。
(3)次数:多项式中____________________。
4.整式:________和________统称为整式。
数字因数
所有字母
单项式
次数最高的项的次数
单项式
多项式
知识点2 整式的运算
1.整式的加减运算
(1)同类项:所含______相同,并且________________也相同的项。
(2)合并同类项:把同类项合并成一项。
(3)合并同类项法则:把同类项的系数相加,字母和字母的______
不变。如 ______。
字母
相同字母的指数
指数
(4)去括号:括号前是“ ”号,去括号后,括号内各项都不变号,如
______ ;括号前是“-”号,去括号后,括号内各项都变号,
如______ 。
(5)整式加减的步骤:先去括号,再合并同类项。
-
-
2.幂的运算,为正整数
(1)同底数幂的乘法:底数不变,指数相加, ______;
(2)同底数幂的除法:____________________, ______
;
(3)幂的乘方:____________________, _____;
(4)积的乘方:把积中的每一个因式分别乘方,再把所得的幂相
乘, ______。
底数不变,指数相减
底数不变,指数相乘
3.整式的乘除运算
(1)单项式乘单项式:把它们的系数、同底数幂分别相乘,对于只
在一个单项式里含有的字母,则连同它的指数作为积的一个因式,如
_______。
(2)单项式乘多项式:根据乘法分配律用单项式去乘多项式的每一
项,再把所得的积相加,如 _______________。
(3)多项式乘多项式:先用一个多项式的每一项乘另一个多项式的
每一项,再把所得的积相加,如 。
(4)乘法公式
完全平方公式:________________________;
平方差公式:_______________________。
(5)单项式除以单项式:把系数与同底数幂分别相除作为商的因式,
对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
(6)多项式除以单项式:先把这个多项式的每一项除以这个单项式,
再把所得的商相加。
4.整式的运算顺序:先算乘方,再算乘除,最后算加减,有括号的先
算括号里面的;同级运算要按照从左到右的顺序依次进行。
知识点3 因式分解
1.定义:把一个多项式化成几个整式的积的形式,这种变形叫作这个
多项式的因式分解,也叫把这个多项式分解因式。
2.因式分解的方法
(1)提公因式法:
系数:取各项系数的____________
字母:取各项相同的____________
次数:取各项相同字母或因式额__________
最大公因数
字母或因式
最低次数
公因式的确定
(2)公式法
完全平方公式:_________, ______
____;
平方差公式: ______________;
立方和(差)公式: 。
3.因式分解的一般步骤
温馨提示 因式分解时一定要分解到每个因式都不能再分解为止。
2025年数学中考复习
专题一 基础夯实
任务1 实数及其运算
知识点1 实数的分类
1.按定义分
2.按正负分
知识点2 实数的相关概念
名称 定义 性质
数轴 规定了 ①______、②________ 和③__________的直线 叫作数轴 (1)数轴上两个点表示的数,右边的
总比左边的④____;(2)数轴上的点
与实数具有⑤__________的关系;
(3)数轴上位于原点两侧,到原点距
离相等的点表示的数⑥____________,
这两个数的⑦________相等
原点
正方向
单位长度
大
一一对应
互为相反数
绝对值
名称 定义 性质
相反数 只有⑧______不同的两 个数互为相反数 (1)互为相反数的两个数, 表示:
____; ___;
(2)0的相反数是 ___
倒数 如果两个数的 _______ ___,那么称这两个数互 为倒数 (1) ___没有倒数;(2)一个非零
数 的倒数为 _ _
符号
0
0
乘积为1
0
续表
名称 定义 性质
绝对值 数轴上表示实数 的点到 原点的 ______叫作实 数的绝对值,记作
注意:绝对值具有非负性
距离
续表
知识点3 实数的大小比较
1.数轴上两个点表示的数,右边的总比左边的____。
2.正数大于0,负数小于0,正数大于一切负数,两个负数中绝对值大
的反而____。
大
小
知识点4 科学记数法
1.科学记数法的表示形式:________。
和 的确定
(1)的确定:是整数位只有一位的数,即 。
(2)的确定:当一个数的绝对值大于10时, 是正整数,其值等于
原数的整数位数_____,或等于原数变为 时,小数点向左移动的位数;当
一个数的绝对值小于1时,是负整数, 的绝对值等于原数左起第一个非
零数字前______________(包括______________),或等于原数变为 时,
小数点向右移动的位数。
减1
所有零的个数
小数点前的零
知识点5 平方根、算术平方根和立方根
1.平方根、算术平方根和立方根
名称 含义 表示 性质
平方 根 如果一个数 的平 方等于 ,那么这个 数叫作 的 ①________ 实数 的 平方根表示 为②_____ (1)一个正数有两个平方根,它
们③____________;0的平方根是
④___;负数没有平方根;
(2)平方根等于它本身的数是⑤
___
平方根
互为相反数
0
0
名称 含义 表示 性质
算术 平方 根 如果一个正数 的 平方等于 ,那么这 个正数叫作 的⑥ ____________ 实数 的 算术平方根 表示为 ⑦____ (1)一个正数有一个正的算术平
方根(双重非负性);0的算术平
方根是⑧___;负数没有算术平方
根;
(2)算术平方根等于它本身的数
是⑨______
算术平方根
0
0和1
续表
名称 含义 表示 性质
立方 根 如果一个数 的立 方等于 ,那么这个 数叫作 的 ⑩________ 实数 的立 方根表示为 ____ (1)所有的数都有一个立方根,
且与原数同号;
(2)立方根等于它本身的数是
_______
立方根
0和
续表
2.开方
(1)求一个数的平方根的运算,叫作开平方,其中 叫作被开方数;
(2)求一个数的立方根的运算,叫作开立方,其中 叫作被开方数。
知识点6 实数的运算
1.加法:(1)同号两数相加,取相同的符号,并把____________;
(2)异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对
值较大的加数的符号,并用较大的绝对值______较小的绝对值。
2.减法:减去一个数,等于加上这个数的________,即
______。
3.乘法:两数相乘,同号得正,异号得负,并把绝对值相乘,即
, 。(注意:任何数与0相乘,积仍为0)
绝对值相加
减去
相反数
4.除法:除以一个不等于0的数,等于乘这个数的倒数,即
__ 。(注意:0除以任何不等于0的数,仍得0)
5.乘方:,表示个 相乘。
(注意:,表示个 相加)
6.实数混合运算的运算顺序:先算乘方,再算乘除,最后算加减,有
括号的先算括号里面的;同级运算要按照从左到右的顺序依次进行。
任务二 整式及因式分解
知识点1 整式的相关概念
1.代数式:用运算符号把数和字母连接而成的式子。
2.单项式:(1)定义:由数或字母的积所组成的代数式叫作单项式。
(单独一个数或字母也是单项式)
(2)系数:单项式中的__________。
(3)次数:单项式中__________指数的和。
3.多项式:(1)定义:几个单项式的和叫作多项式。
(2)项:多项式中的每个________。
(3)次数:多项式中____________________。
4.整式:________和________统称为整式。
数字因数
所有字母
单项式
次数最高的项的次数
单项式
多项式
知识点2 整式的运算
1.整式的加减运算
(1)同类项:所含______相同,并且________________也相同的项。
(2)合并同类项:把同类项合并成一项。
(3)合并同类项法则:把同类项的系数相加,字母和字母的______
不变。如 ______。
字母
相同字母的指数
指数
(4)去括号:括号前是“ ”号,去括号后,括号内各项都不变号,如
______ ;括号前是“-”号,去括号后,括号内各项都变号,
如______ 。
(5)整式加减的步骤:先去括号,再合并同类项。
-
-
2.幂的运算,为正整数
(1)同底数幂的乘法:底数不变,指数相加, ______;
(2)同底数幂的除法:____________________, ______
;
(3)幂的乘方:____________________, _____;
(4)积的乘方:把积中的每一个因式分别乘方,再把所得的幂相
乘, ______。
底数不变,指数相减
底数不变,指数相乘
3.整式的乘除运算
(1)单项式乘单项式:把它们的系数、同底数幂分别相乘,对于只
在一个单项式里含有的字母,则连同它的指数作为积的一个因式,如
_______。
(2)单项式乘多项式:根据乘法分配律用单项式去乘多项式的每一
项,再把所得的积相加,如 _______________。
(3)多项式乘多项式:先用一个多项式的每一项乘另一个多项式的
每一项,再把所得的积相加,如 。
(4)乘法公式
完全平方公式:________________________;
平方差公式:_______________________。
(5)单项式除以单项式:把系数与同底数幂分别相除作为商的因式,
对于只在被除式里含有的字母,则连同它的指数作为商的一个因式。
(6)多项式除以单项式:先把这个多项式的每一项除以这个单项式,
再把所得的商相加。
4.整式的运算顺序:先算乘方,再算乘除,最后算加减,有括号的先
算括号里面的;同级运算要按照从左到右的顺序依次进行。
知识点3 因式分解
1.定义:把一个多项式化成几个整式的积的形式,这种变形叫作这个
多项式的因式分解,也叫把这个多项式分解因式。
2.因式分解的方法
(1)提公因式法:
系数:取各项系数的____________
字母:取各项相同的____________
次数:取各项相同字母或因式额__________
最大公因数
字母或因式
最低次数
公因式的确定
(2)公式法
完全平方公式:_________, ______
____;
平方差公式: ______________;
立方和(差)公式: 。
3.因式分解的一般步骤
温馨提示 因式分解时一定要分解到每个因式都不能再分解为止。
同课章节目录
