10.1 相交线 同步自主提升训练题(含答案)沪科版七年级数学下册
文档属性
| 名称 | 10.1 相交线 同步自主提升训练题(含答案)沪科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 07:08:09 | ||
图片预览


文档简介
沪科版七年级数学下册《 相交线》同步自主提升训练题
1.平面内6条直线两两相交,但仅有3条通过同一点,则截得不重叠线段共( )
A.24条 B.21条 C.33条 D.36条
2.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③平角是一条直线;
④若∠AOC=2∠BOC,则OB是∠AOC的平分线;
⑤三条直线两两相交,只有1个交点.
A.1个 B.2个 C.3个 D.4个
3.若四条直线在平面内交点的个数为a,则a的可能取值有( )
A.3个 B.4个 C.5个 D.6个
4.如图,直线AB,CD交于点O,已知EO⊥AB于点O,OF平分∠BOC,若∠DOE=3∠EOF+5°,则∠AOD的度数是( )
A.71° B.72° C.73° D.74°
5.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
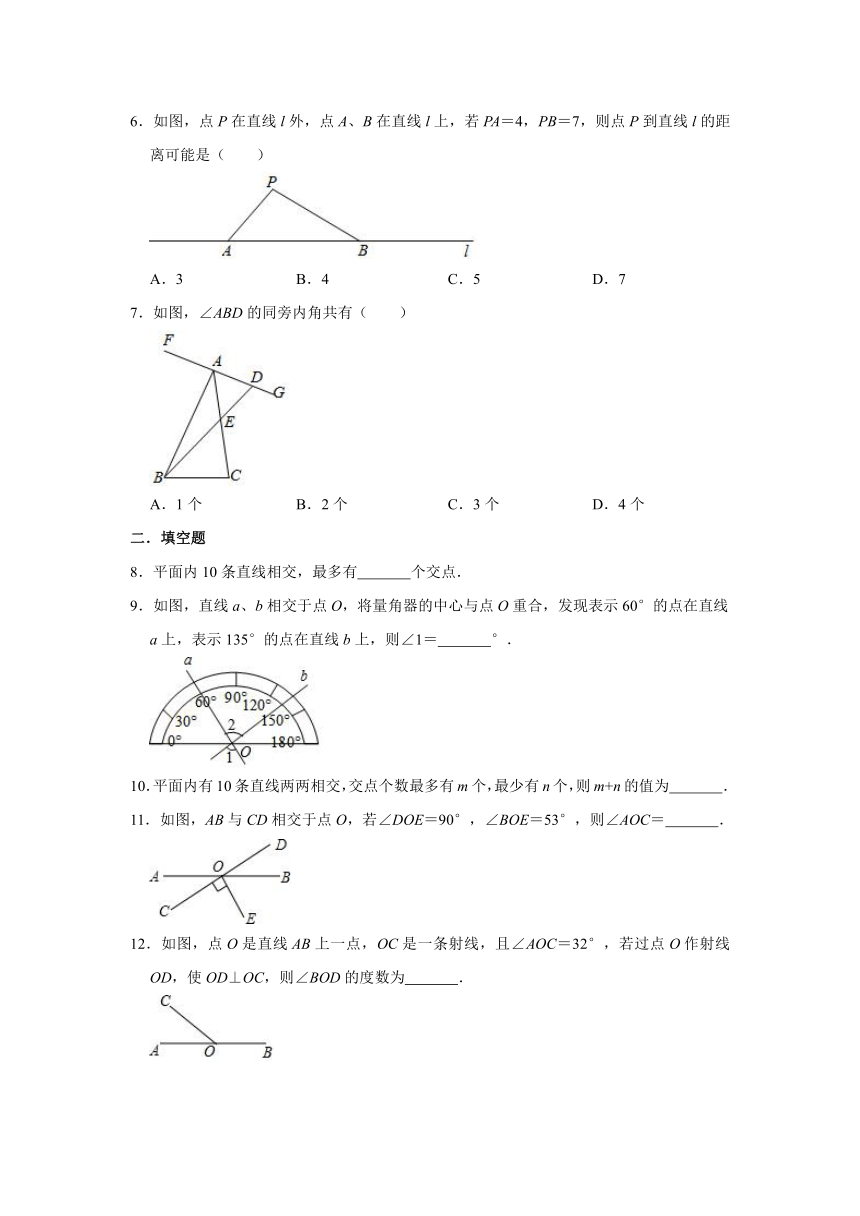
6.如图,点P在直线l外,点A、B在直线l上,若PA=4,PB=7,则点P到直线l的距离可能是( )
A.3 B.4 C.5 D.7
7.如图,∠ABD的同旁内角共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
8.平面内10条直线相交,最多有 个交点.
9.如图,直线a、b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示135°的点在直线b上,则∠1= °.
10.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
11.如图,AB与CD相交于点O,若∠DOE=90°,∠BOE=53°,则∠AOC= .
12.如图,点O是直线AB上一点,OC是一条射线,且∠AOC=32°,若过点O作射线OD,使OD⊥OC,则∠BOD的度数为 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
三.解答题
15.如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
16.如图,
①过点Q作QD⊥AB,垂足为D,
②过点P作PE⊥AB,垂足为E,
③过点Q作QF⊥AC,垂足为F,
④连接P、Q两点,
⑤P、Q两点间的距离是线段 的长度,
⑥点Q到直线AB的距离是线段 的长度,
⑦点Q到直线AC的距离是线段 的长度,
⑧点P到直线AB的距离是线段 的长度.
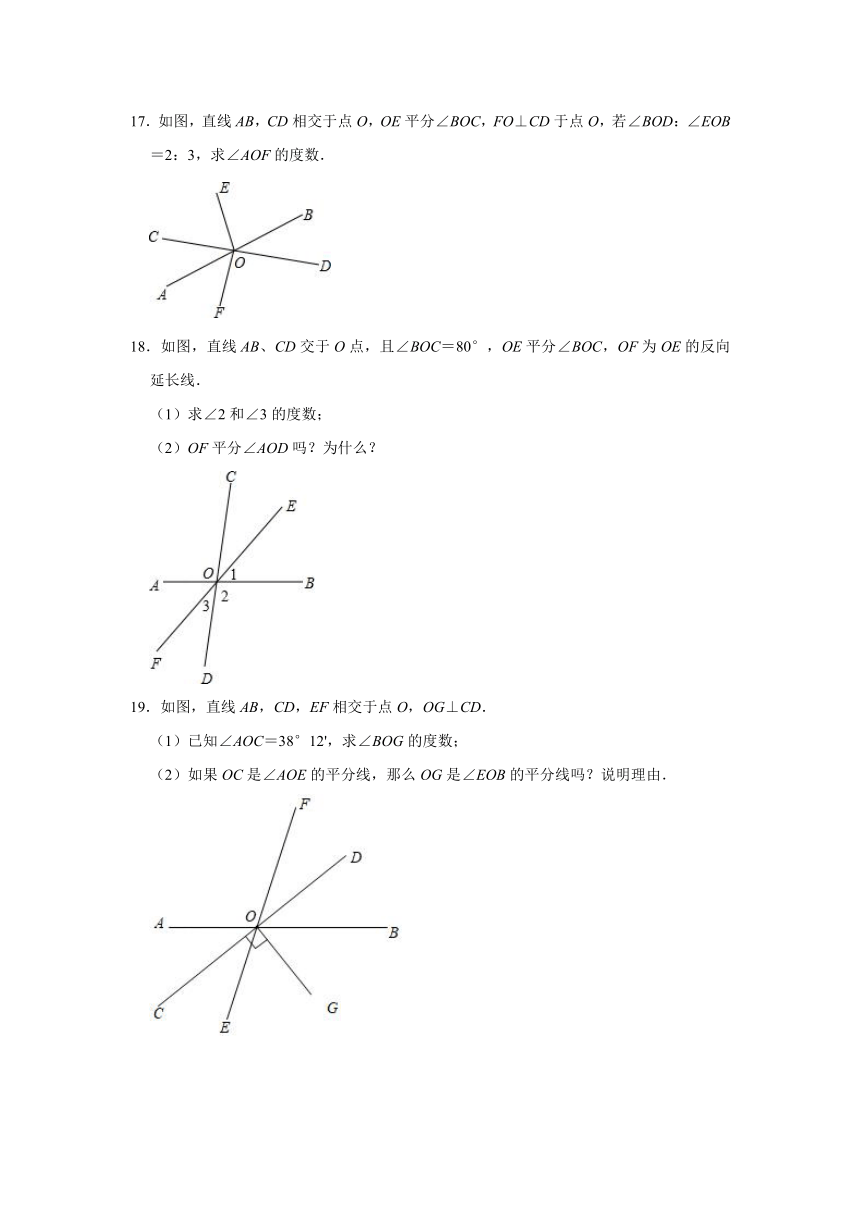
17.如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.
18.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
19.如图,直线AB,CD,EF相交于点O,OG⊥CD.
(1)已知∠AOC=38°12',求∠BOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠EOB的平分线吗?说明理由.
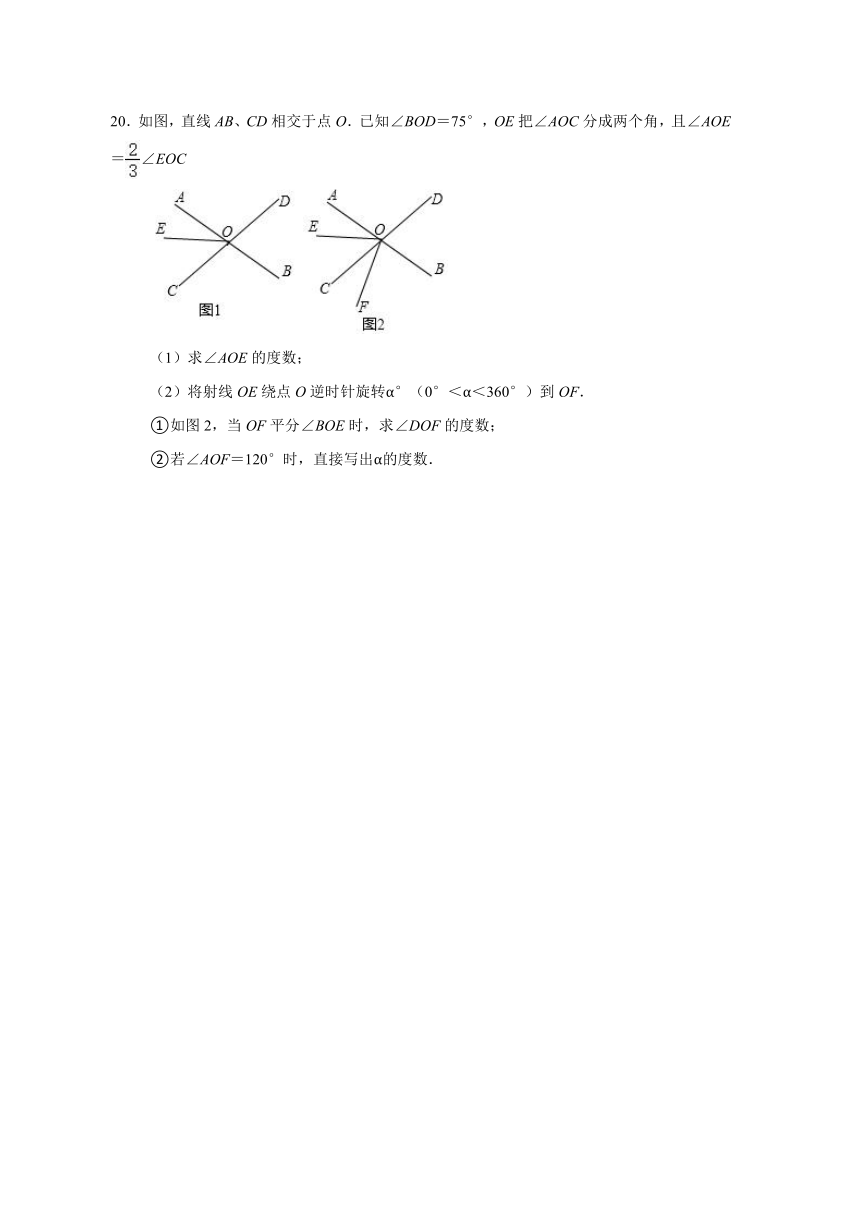
20.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE =∠EOC
(1)求∠AOE的度数;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,求∠DOF的度数;
②若∠AOF=120°时,直接写出α的度数.
参考答案
一.选择题
1.解:AE上共有不重合的线段4条,
AM上共有不重合的线段4条,
BM上共有不重合的线段3条,
CL上共有不重合的线段3条,
DK上共有不重合的线段3条,
EF上共有不重合的线段4条.
共计21条.
故选:B.
2.解:①两点确定一条直线,那么过两点有且只有一条直线,故①正确.
②根据两点间的距离的定义,连接两点的线段的长度叫做两点的距离,故②不正确.
③根据平角定义,平角具有共同顶点且两边在一条直线上,故③不正确.
④根据角平分线的定义,角平分线是从这个角的顶点出发并将这个分成两个相等的角的一条射线,那么若∠AOC=2∠BOC,则OB不一定是∠AOC的平分线,故④不正确.
⑤三条直线两两相交,有3个或1个交点,故⑤不正确.
综上:正确的有①,共1个.
故选:A.
3.解:如图所示:
∴则a的可能取值有0,1,3,4,5,6,共6个.故选:D.
4.解:设∠BOF=x,
∵OF平分∠BOC,
∴∠AOD=∠BOC=2x,
∵EO⊥AB,
∴∠EOA=∠EOB=90°,
∴∠EOF=90°﹣x,∠DOE=2x+90°,
∵∠DOE=3∠EOF+5°,
∴2x+90°=3(90°﹣x)+5°,
解得x=37°,
∴∠AOD=2x=74°.
故选:D.
5.解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
6.解:因为垂线段最短,
∴点P到直线l的距离小于4,
故选:A.
7.解:∠ABD与∠ADB是直线AB、AD,被直线BD所截而成的同旁内角,
∠ABD与∠AEB是直线AB、AC,被直线BD所截而成的同旁内角,
∠ABD与∠BAE是直线AC、BD,被直线AB所截而成的同旁内角,
∠ABD与∠BAD是直线AD、BD,被直线AB所截而成的同旁内角,
故选:D.
二.填空题
8.解:10条直线相交,最多有=45个交点.
故答案为:45.
9.解:∵∠2=135°﹣60°=75°,
∴∠1=∠2=75°,
故答案为:75.
10.解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
11.解:∵∠DOE=90°,∠BOE=53°,
∴∠BOD=90°﹣∠BOE
=90°﹣53°=37°,
又∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=37°,
故答案为:37°.
12.解:∵OD⊥OC,
∴∠COD=90°,
∵∠AOC=32°,
∴∠BOD=180°﹣(90°﹣32°)=122°或∠BOD=180°﹣32°﹣90°=58°,
故答案为:58°或122°.
13.解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
三.解答题
15.解:(1)如图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)∠4和∠5是同旁内角,∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
16.解:①②③④作图如图所示:
⑤根据两点之间距离即可得出P、Q两点间的距离是线段PQ的长度,
⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度,
⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度,
⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度,
故答案为PQ,QD,QF,PE.
17.解:设∠BOD=2x,∠EOB=3x;
∵OE平分∠BOC,
∴∠COE=∠EOB=3x,
则3x+3x+2x=180°,
解得:x=22.5°,
∴∠BOD=45°,
∴∠AOC=∠BOD=45°,
∵FO⊥CD,
∴∠AOF=90°﹣∠AOC=90°﹣45°=45°.
18.解:(1)∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°﹣80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40°.
(2)平分
理由:∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°.
∴∠AOF=∠3=40°,
∴OF平分∠AOD.
19.解:(1)∵OG⊥CD.
∴∠GOC=∠GOD=90°,
∵∠AOC=∠BOD=38°12′,
∴∠BOG=90°﹣38°12′=51°48′,
(2)OG是∠EOB的平分线,
理由:
∵OC是∠AOE的平分线,
∴∠AOC=∠COE=∠DOF=∠BOD,
∵∠COE+∠EOG=∠BOG+∠BOD=90°,
∴∠EOG=∠BOG,
即:OG平分∠BOE.
20.解:(1)∵∠AOE=∠EOC,即∠AOE:∠EOC=2:3.
∴设∠AOE=2x,则∠EOC=3x,
∴∠AOC=5x,
∵∠AOC=∠BOD=75°,
∴5x=75°,
解得:x=15°,
则2x=30°,
∴∠AOE=30°;
(2)①∵∠AOE=30°,
∴∠BOE=180°﹣∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠DOF=75°+75°=150°;
②分两种情况:
当OF在∠BOC的内部时,如图2,
∵∠AOF=120°,∠AOE=30°,
∴α=∠EOF=120°﹣30°=90°,
当OF在∠BOD的内部时,如图3,
∴α=360°﹣∠AOF﹣∠AOE=360°﹣120°﹣30°=210°,
综上所述,α的度数为90°或210°.
1.平面内6条直线两两相交,但仅有3条通过同一点,则截得不重叠线段共( )
A.24条 B.21条 C.33条 D.36条
2.下列说法中正确的有( )
①过两点有且只有一条直线;
②连接两点的线段叫做两点的距离;
③平角是一条直线;
④若∠AOC=2∠BOC,则OB是∠AOC的平分线;
⑤三条直线两两相交,只有1个交点.
A.1个 B.2个 C.3个 D.4个
3.若四条直线在平面内交点的个数为a,则a的可能取值有( )
A.3个 B.4个 C.5个 D.6个
4.如图,直线AB,CD交于点O,已知EO⊥AB于点O,OF平分∠BOC,若∠DOE=3∠EOF+5°,则∠AOD的度数是( )
A.71° B.72° C.73° D.74°
5.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短
6.如图,点P在直线l外,点A、B在直线l上,若PA=4,PB=7,则点P到直线l的距离可能是( )
A.3 B.4 C.5 D.7
7.如图,∠ABD的同旁内角共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
8.平面内10条直线相交,最多有 个交点.
9.如图,直线a、b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示135°的点在直线b上,则∠1= °.
10.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
11.如图,AB与CD相交于点O,若∠DOE=90°,∠BOE=53°,则∠AOC= .
12.如图,点O是直线AB上一点,OC是一条射线,且∠AOC=32°,若过点O作射线OD,使OD⊥OC,则∠BOD的度数为 .
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
三.解答题
15.如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.
(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;
(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?
16.如图,
①过点Q作QD⊥AB,垂足为D,
②过点P作PE⊥AB,垂足为E,
③过点Q作QF⊥AC,垂足为F,
④连接P、Q两点,
⑤P、Q两点间的距离是线段 的长度,
⑥点Q到直线AB的距离是线段 的长度,
⑦点Q到直线AC的距离是线段 的长度,
⑧点P到直线AB的距离是线段 的长度.
17.如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.
18.如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
19.如图,直线AB,CD,EF相交于点O,OG⊥CD.
(1)已知∠AOC=38°12',求∠BOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠EOB的平分线吗?说明理由.
20.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE =∠EOC
(1)求∠AOE的度数;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,求∠DOF的度数;
②若∠AOF=120°时,直接写出α的度数.
参考答案
一.选择题
1.解:AE上共有不重合的线段4条,
AM上共有不重合的线段4条,
BM上共有不重合的线段3条,
CL上共有不重合的线段3条,
DK上共有不重合的线段3条,
EF上共有不重合的线段4条.
共计21条.
故选:B.
2.解:①两点确定一条直线,那么过两点有且只有一条直线,故①正确.
②根据两点间的距离的定义,连接两点的线段的长度叫做两点的距离,故②不正确.
③根据平角定义,平角具有共同顶点且两边在一条直线上,故③不正确.
④根据角平分线的定义,角平分线是从这个角的顶点出发并将这个分成两个相等的角的一条射线,那么若∠AOC=2∠BOC,则OB不一定是∠AOC的平分线,故④不正确.
⑤三条直线两两相交,有3个或1个交点,故⑤不正确.
综上:正确的有①,共1个.
故选:A.
3.解:如图所示:
∴则a的可能取值有0,1,3,4,5,6,共6个.故选:D.
4.解:设∠BOF=x,
∵OF平分∠BOC,
∴∠AOD=∠BOC=2x,
∵EO⊥AB,
∴∠EOA=∠EOB=90°,
∴∠EOF=90°﹣x,∠DOE=2x+90°,
∵∠DOE=3∠EOF+5°,
∴2x+90°=3(90°﹣x)+5°,
解得x=37°,
∴∠AOD=2x=74°.
故选:D.
5.解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连接直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
6.解:因为垂线段最短,
∴点P到直线l的距离小于4,
故选:A.
7.解:∠ABD与∠ADB是直线AB、AD,被直线BD所截而成的同旁内角,
∠ABD与∠AEB是直线AB、AC,被直线BD所截而成的同旁内角,
∠ABD与∠BAE是直线AC、BD,被直线AB所截而成的同旁内角,
∠ABD与∠BAD是直线AD、BD,被直线AB所截而成的同旁内角,
故选:D.
二.填空题
8.解:10条直线相交,最多有=45个交点.
故答案为:45.
9.解:∵∠2=135°﹣60°=75°,
∴∠1=∠2=75°,
故答案为:75.
10.解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
11.解:∵∠DOE=90°,∠BOE=53°,
∴∠BOD=90°﹣∠BOE
=90°﹣53°=37°,
又∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=37°,
故答案为:37°.
12.解:∵OD⊥OC,
∴∠COD=90°,
∵∠AOC=32°,
∴∠BOD=180°﹣(90°﹣32°)=122°或∠BOD=180°﹣32°﹣90°=58°,
故答案为:58°或122°.
13.解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为:PM,垂线段最短.
14.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
三.解答题
15.解:(1)如图所示:同位角共有5对:
分别是∠1和∠5,∠2和∠3,∠3和∠7,∠4和∠6,∠4和∠9;
(2)∠4和∠5是同旁内角,∠6和∠8也是同旁内角,故∠6和∠8之间的位置关系与∠4和∠5的相同.
16.解:①②③④作图如图所示:
⑤根据两点之间距离即可得出P、Q两点间的距离是线段PQ的长度,
⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度,
⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度,
⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度,
故答案为PQ,QD,QF,PE.
17.解:设∠BOD=2x,∠EOB=3x;
∵OE平分∠BOC,
∴∠COE=∠EOB=3x,
则3x+3x+2x=180°,
解得:x=22.5°,
∴∠BOD=45°,
∴∠AOC=∠BOD=45°,
∵FO⊥CD,
∴∠AOF=90°﹣∠AOC=90°﹣45°=45°.
18.解:(1)∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°﹣80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40°.
(2)平分
理由:∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°.
∴∠AOF=∠3=40°,
∴OF平分∠AOD.
19.解:(1)∵OG⊥CD.
∴∠GOC=∠GOD=90°,
∵∠AOC=∠BOD=38°12′,
∴∠BOG=90°﹣38°12′=51°48′,
(2)OG是∠EOB的平分线,
理由:
∵OC是∠AOE的平分线,
∴∠AOC=∠COE=∠DOF=∠BOD,
∵∠COE+∠EOG=∠BOG+∠BOD=90°,
∴∠EOG=∠BOG,
即:OG平分∠BOE.
20.解:(1)∵∠AOE=∠EOC,即∠AOE:∠EOC=2:3.
∴设∠AOE=2x,则∠EOC=3x,
∴∠AOC=5x,
∵∠AOC=∠BOD=75°,
∴5x=75°,
解得:x=15°,
则2x=30°,
∴∠AOE=30°;
(2)①∵∠AOE=30°,
∴∠BOE=180°﹣∠AOE=150°,
∵OF平分∠BOE,
∴∠BOF=75°,
∵∠BOD=75°,
∴∠DOF=75°+75°=150°;
②分两种情况:
当OF在∠BOC的内部时,如图2,
∵∠AOF=120°,∠AOE=30°,
∴α=∠EOF=120°﹣30°=90°,
当OF在∠BOD的内部时,如图3,
∴α=360°﹣∠AOF﹣∠AOE=360°﹣120°﹣30°=210°,
综上所述,α的度数为90°或210°.
