第三章《圆》复习题 弧、弦、圆心角的关系(含解析) 九年级数学下册北师大版
文档属性
| 名称 | 第三章《圆》复习题 弧、弦、圆心角的关系(含解析) 九年级数学下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 22:28:33 | ||
图片预览


文档简介
第三章《圆》复习题--弧、弦、圆心角的关系
【题型1 由弧、弦、圆心角的关系判断结论正误】
1.如图,是的直径,点P是上一个动点(点P不与点A,B重合),在点P运动的过程中,对于如下结论:①的值为定值;②的度数为定值;③的度数始终等于度数的2倍;④若,则.正确的结论有( )
A.4个 B.3个 C.2个 D.1个
2.下列说法正确的个数有( )
①半圆是弧;
②面积相等的两个圆是等圆;
③所对的弦长相等的两条弧是等弧;
④如果圆心角相等,那么它们所对的弦一定相等;
⑤等弧所对的圆心角相等;
⑥平分弦的直径,平分这条弦所对的弧.
A.2个 B.3个 C.4个 D.5个
3.如图所示,在中,,那么( )
A. B. C. D.无法比较
4.平分锐角,以为圆心以任意长为半径画,分别交,,于A,B,C三点,以C为圆心,以长为半径画弧与相交于异于B点的点D,连接,.下列结论错误的是( )
A. B.若,则
C. D.
【题型2 利用弧、弦、圆心角的关系求线段长度】
1.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=6,则点O到弦AB的距离为( )
A.6 B.8 C.3 D.4
2.如图,在中,圆心角是的中点,作,与交于,则图中与相等的线段有 条.
3.如图,是⊙O的直径,点C为圆上一点,,D是弧的中点,与交于点E.若E是的中点,则的长为( )
A.5 B.3 C.2 D.1
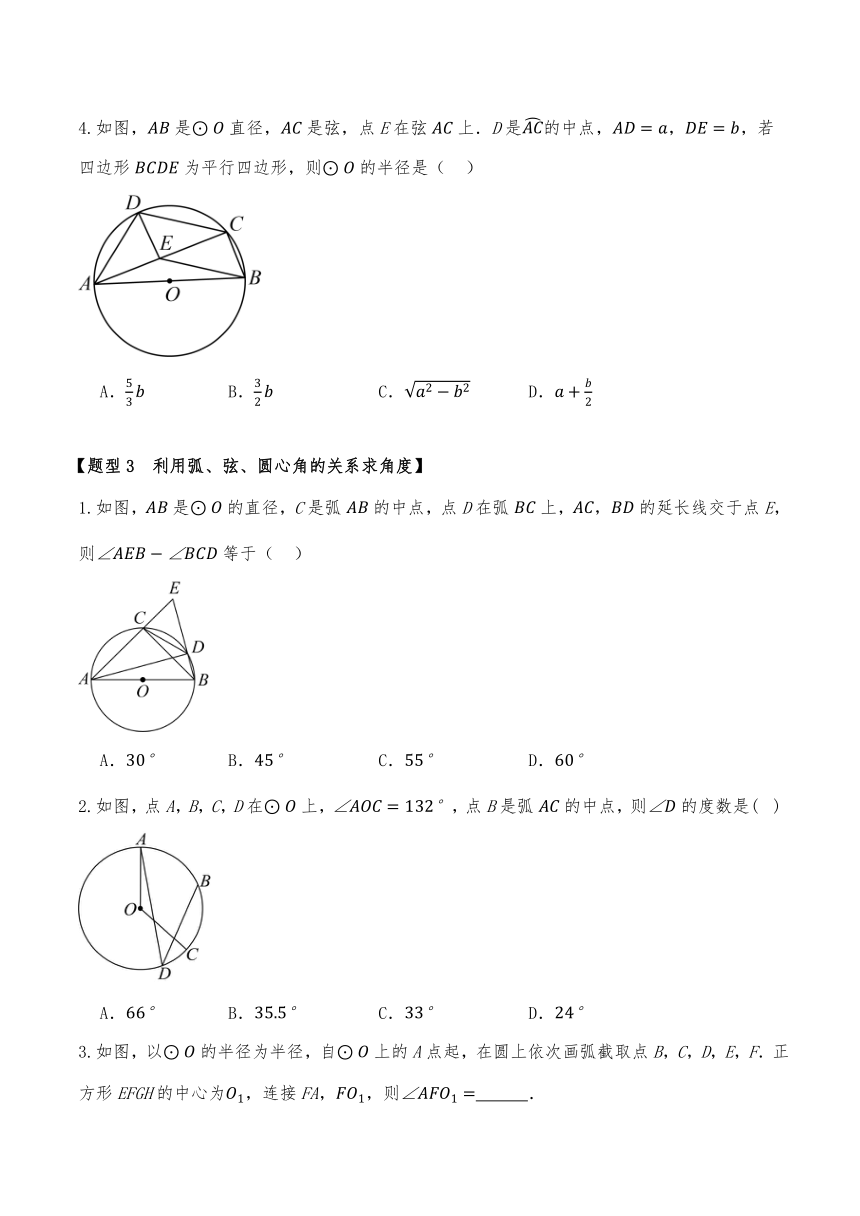
4.如图,是直径,是弦,点E在弦上.D是的中点,,,若四边形为平行四边形,则的半径是( )
A. B. C. D.
【题型3 利用弧、弦、圆心角的关系求角度】
1.如图,是的直径,C是弧的中点,点D在弧上,的延长线交于点E,则等于( )
A. B. C. D.
2.如图,点A,B,C,D在上,,点B是弧的中点,则的度数是( )
A. B. C. D.
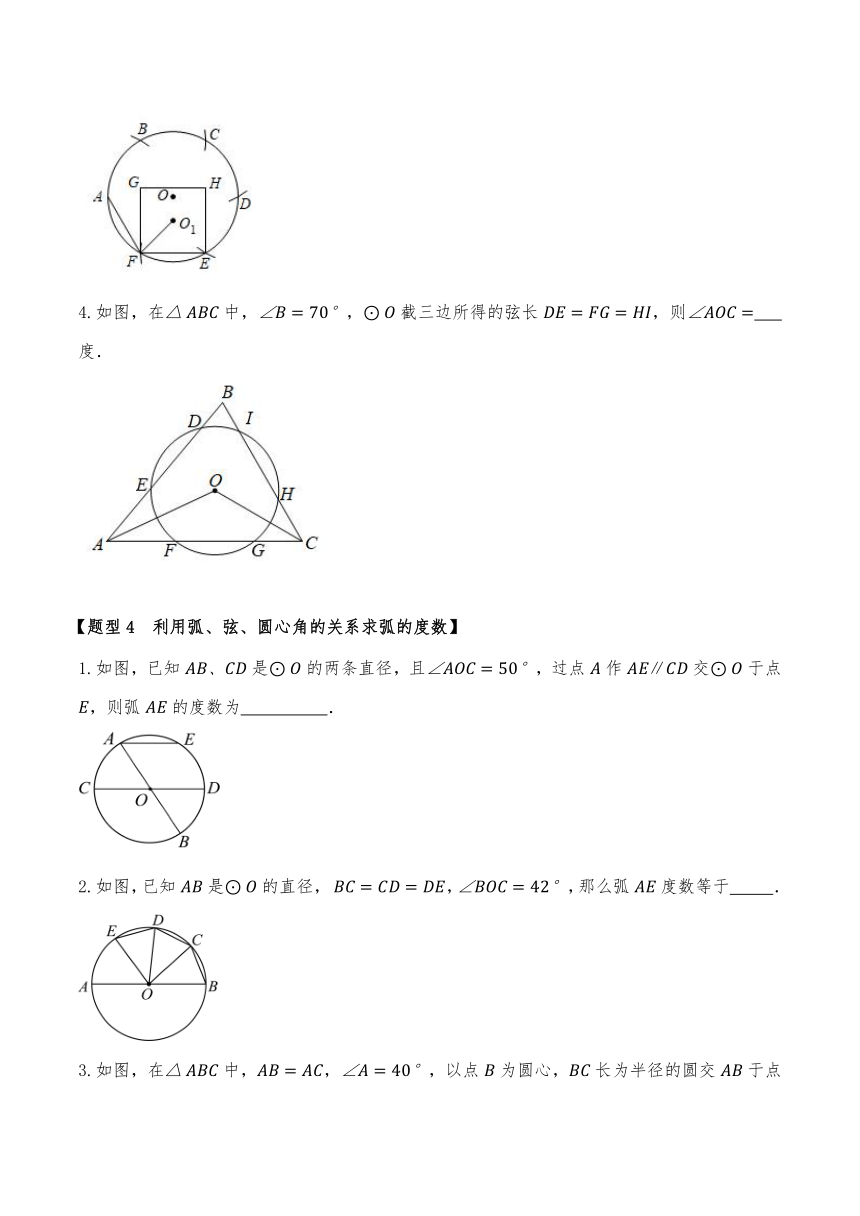
3.如图,以的半径为半径,自上的A点起,在圆上依次画弧截取点B,C,D,E,F.正方形EFGH的中心为,连接FA,,则 .
4.如图,在中,,截三边所得的弦长,则 度.
【题型4 利用弧、弦、圆心角的关系求弧的度数】
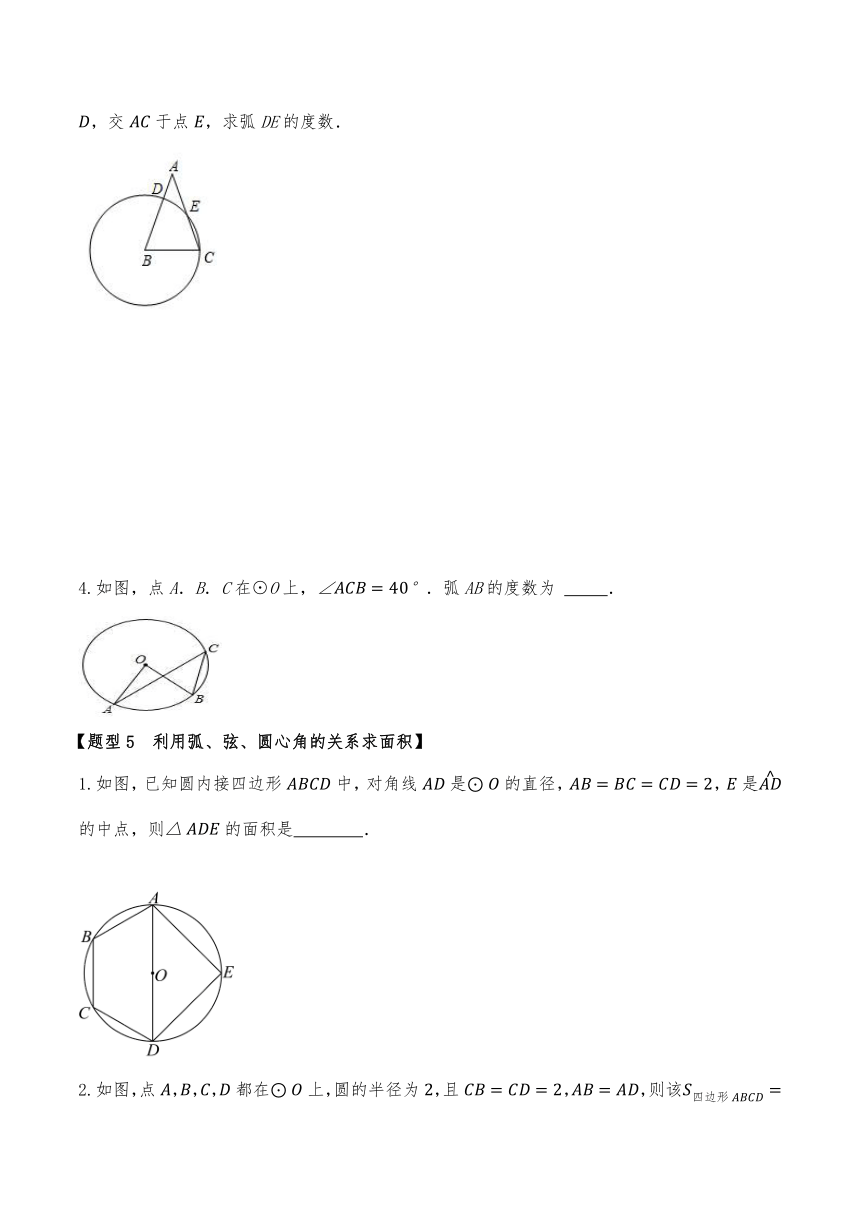
1.如图,已知是的两条直径,且,过点作交于点,则弧的度数为 .
2.如图,已知是的直径, ,,那么弧度数等于 .
3.如图,在中,,以点为圆心,长为半径的圆交于点,交于点,求弧DE的度数.
4.如图,点A.B.C在⊙O上,.弧AB的度数为 .
【题型5 利用弧、弦、圆心角的关系求面积】
1.如图,已知圆内接四边形中,对角线是的直径,,是的中点,则的面积是 .
2.如图,点,,,都在上,圆的半径为,且,,则该( )
A. B. C. D.
3.如图,以等边的一边为直径的半圆交于点,交于点,若,则阴影部分的面积是( )
A. B. C. D.
4.已知:是的直径,C为上一点,将绕着点B逆时针旋转一定的角度得到,交于E点,若点D在上,连接交于点F.
(1)直接判断与的位置关系;
(2)求证:;
(3)若,,求阴影部分的面积.
【题型6 利用弧、弦、圆心角的关系求周长】
1.如图所示,是半径为3的上的两点.若是的中点,则四边形的周长为 .
2.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的周长为 .
3.如图的弦,且于,连接,若,则的周长为( )
A. B. C. D.
4.如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
【题型7 利用弧、弦、圆心角的关系求线段比值】
1.如图, 将上的 沿弦翻折交半径于点D, 再将沿 翻折交于点E, 连接. 若, 则 的值 .
2.如图,在中,点C是劣弧的中点,点P在劣弧上,且,于H,当,则 .
3.如图,、、、依次为一直线上个点,,为等腰直角三角形,且,过点、、,且弧的度数,则的值是 .
4.如图,等边内接于,D为边上一动点(不与A、C重合),连接并延长交边于E,将沿翻折为,边交于点,若的周长记为,的周长记为,则的值为 .
【题型8 利用弧、弦、圆心角的关系进行证明】
1.(1)如图①,过上一点作两条弦、,若,则平分,为什么?
(2)如图②,若点在内,过点的两条弦,相等,则平分吗?为什么?
(3)如图③,若点在外,过点作、,分别交于点,和,,且,则平分吗?为什么?
2.如图,、是的两条弦,与相交于点E,.
(1)求证:;
(2)连接 作直线求证:.
3.如图,四边形是的内接四边形,直径平分.
(1)求证:;
(2)过点A向圆外作,且,求证:四边形为平行四边形.
4.如图,以为直径的圆O中,点O为圆心,C为弧的中点,过点C作且.连接,分别交,于点E,F,与圆O交于点G,连接.
(1)求证:;
(2)连接,,求证:.
【题型9 利用弧、弦、圆心角的关系判断线段或弧长间的关系】
1.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是( )
A. B. C. D.不能确定
2.从圆内一点引两条弦与,则与、度数间的关系是 .
3.如图,圆上有A,B,C,D四点,圆内有E,F两点且点E,F在BC上.若四边形AEFD为正方形,则下列弧长关系中,正确的是( )
A. B. C. D.
4.将一张正方形的透明纸片ABCD和按如图位置叠放,顶点A、D在上,边AB、BC、CD分别与相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B.
C. D.
【题型10 利用弧、弦、圆心角的关系求最值】
1.如图,是半圆O的直径,半圆的半径为4,点C,D在半圆上,,点P是上的一个动点,则的最小值为 .
2.)如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
3.如图,AB是O的直径,AB=4,C为的三等分点(更靠近A点),点P是O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
4.如图,是的直径,,点M在上,,N是弧的中点,P是直径上的一动点.若,则周长的最小值为 .
参考答案
【题型1 由弧、弦、圆心角的关系判断结论正误】
1.C
【分析】本题考查主要考查了圆心角、弧、弦的关系,圆周角定理等知识,熟记圆中有关观念时解本题的关键.根据圆周角定理,圆心角,弧,弦之间的关系解决问题即可.
【详解】解:①由题可得:当点P从点A运动到的中点时,的值在增大,当点P从的中点运动到点B时,的值在减小,
故①错误;
②时直径,
,
的度数为定值,
②正确;
③,
,
,
的度数始终等于度数的2倍,
③正确;
④如图,取的中点,连接,,,则,
,
,
,
,
,
④错误;
正确的结论个数是2个,
故选:C
2.B
【分析】根据半圆的定义判断①;根据圆的面积公式和等圆的定义判断②;根据圆心角、弧、弦的关系判断③④⑤;根据垂径定理的推论判断⑥.
【详解】解:半圆是弧,故①正确;
面积相等的两个圆半径相等,因此是等圆,故②正确;
在同圆或等圆中,所对的弦长相等的两条劣弧是等弧,两条优弧是等弧,故③错误;
在同圆或等圆中,如果圆心角相等,那么它们所对的弦一定相等,故④错误;
等弧所对的圆心角相等,故⑤正确;
平分弦(非直径)的直径,平分这条弦所对的弧,故⑥错误;
综上可知,正确的有①②⑤,共3个,
故选B.
3.B
【分析】本题考查了圆心角、弧、弦之间的关系和三角形的三边关系,在圆上截取,再根据“根据三角形的三边关系”可解,熟练掌握圆心角、弧、弦之间的关系和三角形的三边关系是解题的关键.
【详解】解:如图,
在圆上截取,
∵,
∴,
∴,
根据三角形的三边关系知,,
∴,
故选:.
4.D
【分析】先根据题意画好图形,如图,连接,,由角平分线的定义结合圆心角,弧,弦之间的关系,判断A;证明为等边三角形,可判断B;连接,证明,可判断C;连接,可得,可判断D ,从而可得答案.
【详解】解:如图,连接,,
∵平分锐角,
∴,
∴,故A不符合题意;
∵由作图可得,
∴,
∴,
∵,,
∴为等边三角形,
∴,
∴,故B不符合题意;
连接,
∵,,
∴,
∴,故C不符合题意;
连接,
∵,,
∴,
∴,故D符合题意.
故选D.
【题型2 利用弧、弦、圆心角的关系求线段长度】
1.C
【分析】延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,根据垂径定理求出DH=HC=3,DF=EF,根据三角形的中位线求出DE=2OH,根据勾股定理求出OH长,再根据勾股定理求出OF长即可.
【详解】解:延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,
∵∠COD和∠DOE互补,∠COD和∠AOB互补,
∴∠DOE=∠AOB,
∴DE=AB,OF=OG,
∵OH⊥DC,CD=6,OH过O,
∴DH=HC=DC=3,∠OHD=∠OHC=90°,
由勾股定理得:OH===4,
∵OC=OE,DH=HC,OH=4,
∴DE=2OH=8,
∵OF⊥DE,OF过O,
∴DF=EF=DE=4,
在Rt△DFO中,由勾股定理得:OF===3,
∴OG=OF=3,
即点O到AB的距离是3,
故选:C.
2.3
【分析】此题考查了圆心角、弧、弦的关系,等边三角形的性质与判定;连接,,根据圆心角、弧的关系求出,根据圆周角定理求出,根据直角三角形的性质求出,再根据等边三角形的判定与性质求解即可.
【详解】解:如图,连接,,
,是的中点,
,
,
,
,
,
,
是等边三角形,
,,
,,
是等边三角形,
,
,
图中与相等的线段有条,
故答案为:.
3.C
【分析】
连接交于F,由垂径定理得,,可证,接着证明得到,计算得,然后设,则,,最后利用勾股定理计算得到BC的长.
【详解】
解:连接交于F,如图,
D是弧的中点,
,
,
是直径,
,
,
,
E是的中点,
,
,
,
,
,
,
,
设,则,
,
在中,,
,
解得,
即,
故选:C.
4.B
【分析】等弧对等弦,得到,得到三角形为等腰三角形,圆周角定理得到,平行四边形的性质,得到,三线合一得到点为的中点,连接,中位线定理,得到,垂径定理得到,进而得到三点共线,即可得出的半径.
【详解】解:∵是直径,
∴,
∵D是的中点,
∴,
∴,
∵四边形为平行四边形,
∴,,
∴,
∴,
∵,
∴,
则:点为的中点,
连接,则:,,
∵,
∴三点共线,
∴;即的半径是.
故选B.
【题型3 利用弧、弦、圆心角的关系求角度】
1.B
【分析】由是的直径,则可得,已知C是弧的中点,则,根据圆周角定理可知,故,根据 即可解答.
【详解】解:∵是的直径,
∴,
∴,
∵C是弧的中点,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:B.
2.C
【分析】本题考查了同弧或等弧所对的圆心角相等,圆周角定理.熟练掌握同弧或等弧所对的圆心角相等,圆周角定理是解题的关键.
如图,连接,则,,由圆周角定理可得,计算求解即可.
【详解】解:如图,连接,
∵点B是弧的中点,
∴,
∴,
∵,
∴,
故选:C.
3.75°
【分析】连接OA,OF,OE,根据等边三角形的判定和性质,圆心角、弧、弦关系,求得∠AFE=120°,再根据正方形的性质求得∠O1FE=45°,计算角的差即可解答;
【详解】解:如图,连接OA,OF,OE,
∵FE=OF=OE,∴△OFE是等边三角形,∴∠OFE=60°,∴弧FE=60°,
由圆心角、弧、弦关系可得弧FE=弧ED=弧DC=弧CB=弧BA=60°,
∴弧AF=360°-60°×5=60°,∴∠AOF=60°,
∵OA=OF,∴△OAF是等边三角形,∴∠AFO=60°,
∴∠AFE=∠AFO+∠OFE=120°,
∵O1是正方形的中心,∴∠O1FE=45°,
∴∠AFO1=∠AFE -∠O1FE=75°,
故答案为:75°;
4.125
【分析】过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,由于=,利用弦、圆心角和对应的弦心距的关系得到OM=OK=OP,则可判断OA平分∠BAC,OC平分∠ACB,然后根据角平分线的定义和三角形内角和求解.
【详解】解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC+∠OCA=(∠BAC+∠ACB)=(180°∠B)=90° ,
∴∠AOC=180°(∠OAC+∠OCA)
=180°
=125°.
故答案为:125.
【题型4 利用弧、弦、圆心角的关系求弧的度数】
1.
【分析】本题考查平行线的性质,圆心角,弧,弦之间的关系,圆周角定理等知识点,
连接,根据平行线的性质求出,根据圆周角定理求出,再求出的度数,即可求出本题答案.
【详解】解:连接,
∵,,
∴,
∵,
∴
∴,
∴的度数是,
∵是的两条直径,
∴的度数是,
∴的度数是,
故答案为:.
2.
【分析】本题主要考了圆心角、弧、弦的关系.注意掌握数形结合思想的应用.
根据圆心角与弧的关系可求得的度数,从而即可求解.
【详解】∵
∴,
∴,
∴,
∴弧度数等于.
故答案为:.
3.
【分析】连接,如图,先根据等腰三角形的性质和三角形内角计算出,再利用得到,然后根据三角形外角性质计算出,从而得到弧的度数.
【详解】解:连接,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴弧的度数为.
4.
【分析】在⊙O中,和对着同一条弧,根据圆周角定理,可得出的度数,再根据弧与圆心角的关系即可得到答案.
【详解】解:在⊙O中,和对着同一条弧,
又,
,
因为弧的度数和它所对的圆心角的度数相等,
所以的度数为.
故答案为:.
【题型5 利用弧、弦、圆心角的关系求面积】
1.4
【分析】四边形ABCD是梯形,连接OB,则OBCD是菱形,即可求得AD的长,而△AED是等腰直角三角形,就可求得△ADE的面积.
【详解】解:连接EO,BO,CO
∵AB=BC=CD=2,
∴∠AOB=180÷3=60°,
∴△AOB是等边三角形,
那么OA=AB=2,那么AD=2OA=4.
∵E是的中点,
∴AE=DE,
∴EO⊥AD,
∵EO=2,
∴△ADE的面积=×4×2=4.
故答案为4
2.A
【分析】本题考查了圆周角定理,圆心角、 弧、 弦之间的关系,勾股定理.连接, 求出,求出是圆的直径,根据勾股定理求出,根据计算是解题的关键.
【详解】解:连接,
,
,,
,
即是圆的直径,
,
∵圆的半径为,
,
,
由勾股定理得:
,
∴,
故选:A.
3.A
【分析】连接,,,可得,,都是等边三角形,从而得弓形的面积弓形的面积,进而得阴影部分的面积的面积,进而即可求解.
【详解】连接,,,
是等边三角形,
,,
,
,,,都是等边三角形,
,
弓形的面积弓形的面积,
阴影部分的面积的面积,
,
是等边三角形,边长为,
过点作于点,则, ,
的面积 ,
阴影部分的面积 .
故选:A.
4.(1)解:
将绕着点B逆时针旋转一定的角度得到,交于E点,所以所在的圆与是等圆,连接
∴,
∴点B是中点,
∵是的直径,
∴;
(2)证明:连接,
∵,所在的圆与是等圆,
∴,
∴,
∵,
∴;
(3)解:由(2)得,,所在的圆与是等圆,
所以弓形和弓形的面积相等,阴影部分的面积就是三角形的面积,
连接,
∵,,
∴,
∴,
∴,
所以三角形的面积=,
阴影面积为:
【题型6 利用弧、弦、圆心角的关系求周长】
1.12
【分析】通过等弧所对的圆心角相等和,得到和都是等边三角形,再求出四边形的周长.
【详解】解:连接,
∵C是的中点,
∴,
∵,
∴,
∵,
∴和都是等边三角形,
∴,
∴四边形的周长等于为.
故答案为:.
2.8cm
【分析】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为DA=4cm;然后由圆的周长公式进行计算.
【详解】解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).
故答案为:8πcm.
3.A
【分析】连接AB、OA、OD,然后由弦与弧的关系,求出,得到,再根据勾股定理求出半径,即可得到答案.
【详解】解:连接AB、OA、OD,如图,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
在直角△AOD中,设OA=OD=R,
∵,
∵,
∴,
∴,
∴圆的周长为:;
故选:A.
4.A
【分析】连接,依题意得,,的周长为,四边形的周长为,故,根据的三边关系即可得解.
【详解】连接,
∵点是的八等分点,即
∴,
∴
又∵的周长为,
四边形的周长为,
∴
在中有
∴
故选A.
【题型7 利用弧、弦、圆心角的关系求线段比值】
1.
【分析】本题主要考查折叠的性质,等腰三角形的性质,圆周角定理及弧,弦,圆心角之间的关系,勾股定理.连接、、,作于F,设,则,,,先利用折叠的性质和圆周角定理得到 ,再利用弧、弦、圆心角的关系得到,然后利用勾股定理计算出,接着再计算出即可.
【详解】解:连接、、,作于F,如图所示,
设,则,,
∴,
∵上的沿弦翻折交半径于点D,再将沿 翻折交于点E,
∴为等圆中的弧,
∵它们所对的圆周角为,
∴,
∴,
∴,
∴,
在中,,
在中,,
,
∴.
故答案为:.
2.
【分析】在上截取,连接,可以证明,得到,由,得到,由圆周角定理得到,因此,得到,即可求解.
【详解】在上截取,连接,
∵C是的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴,
故答案为:.
3.
【分析】本题考查了等腰直角三角形的性质,弧与圆心角的关系,矩形的性质,勾股定理,正确作辅助线是解题关键;连接,延长交分别为,得到是等腰直角三角形,则四边形是矩形,是等腰直角三角形,设,则,进而表示出,根据勾股定理建立关系式,整理得出,即可求解.
【详解】如图所示,连接,延长交分别为,
∵,为等腰直角三角形
∴,
∵弧的度数,
∴是等腰直角三角形,
则四边形是矩形,是等腰直角三角形,
设,则,
∴,
在中,
∴
即
整理得,
∴
故答案为:.
4.
【分析】此题考查了折叠的性质,圆周定理,等边三角形的性质,连接,,延长交于点,连接,由折叠性质可知:,则,从而有,通过弧度和差可得,所以,再由周长即可求解.在同圆或等圆中,等弧所对的圆心角、弦相等,解题的关键是熟练掌握以上知识的应用.
【详解】如图,连接,,延长交于点,连接,
由折叠性质可知:,
∴,
∵,
∴,即,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴,
∴,
∴,
设,
∴的周长,
的周长,
∴,
故答案为:.
【题型8 利用弧、弦、圆心角的关系进行证明】
1.解:(1)平分,
如图,作直径,
,
,
,
,
平分;
(2)平分.理由如下:
作于,于,连接、,如图,
则,,
,
,
而,,
,
平分;
(3)平分.理由如下:
作于,于,连接、,如图,
则,,同理(2)可得,
平分.
2.(1)证明:∵,
∴
∴,
即.
∴.
(2)证明:连接
∵
∴
∴
∴
∵
∴E、O都在的垂直平分线上.
∴
3.(1)证明:为直径,
,
直径平分,
,
,
,
,
;
(2)证明:
四边形为平行四边形.
4.(1)证明:∵,,
∴四边形为平行四边形,
∵为半圆的中点,
∴,即,
∴平行四边形为矩形.
∴,
∴.
(2)证明:连接,,交于,
由(1)可知平行四边形为矩形,
∵,
∴四边形为正方形,则,,
∵,
∴,
∴,
∵,
∴,
∵,,
∴垂直平分,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
【题型9 利用弧、弦、圆心角的关系判断线段或弧长间的关系】
1.【分析】连接OC,BC,过O作OE⊥AC于D交圆O于E,根据折叠的性质得到ODOE,根据圆周角定理得到∠ACB=90°,根据三角形的中位线的性质得到ODBC,求得∠COB=60°,得到∠AOC=120°,于是得到结论.
【解答】解:如图,连接OC,BC,过O作OE⊥AC于D交圆O于E,
∵把半圆沿弦AC折叠,恰好经过点O,
∴ODOE,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴OD∥BC,
∵OA=OB,
∴ODBC,
∴BC=OE=OB=OC,
∴∠COB=60°,
∴∠AOC=120°,
∴,
故选:A.
2.(的度数 的度数)
【分析】本题考查了圆心角、弧、弦之间的转化,圆周角的度数等于它所对的弧的度数.连,根据三角形外角性质得到,而的度数,的度数,由此得到与、度数间的关系.
【详解】解:如图,连,
,
又的度数,的度数,
(的度数 的度数).
3.C
【分析】由图知,BC>AD,根据大弦对大弧知, .
【详解】A、因为四边形AEFD为正方形,所以AD=AE,则其所对的弧相等,因为AB>AE,所以,故A项不正确;
B、因为四边形AEFD为正方形,所以AD=AE,因为AB>AE,所以AB>AD,则可得 ,故B项不正确;
C、弦AB<AE+BE(三角形两边之和大于第三边),弦BC=EF+BE+FC>EF+BE=AE+BE>弦AB,所以,故C项正确;
D、由图可看出其不相等,故D项错误.
故答案选:C.
4.C
【分析】连接,根据弦与弧的关系,只要比较弦长即可比较弧长的大小即可求解.
【详解】如图,连接,过点作,交于,交于,则,
四边形是正方形,
,,
,
四边形是矩形,
,
,
,
,
,
A. , ,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. , ,故该选项正确,符合题意;
D., ,故该选项不正确,不符合题意;
故选:C.
【题型10 利用弧、弦、圆心角的关系求最值】
1.
【分析】依题意,作点关于的对称点为,连接,长即为最小值;过点作,构造和进行对应线段求解;
【详解】作点关于的对称点为,连接,;过点作;
由题知,,,∴,可得对应的圆心角;
又点关于的对称点为,
∴,,∴长为的最小值
在中,,∴,;
在中,,,∴;
故填:;
2.B
【分析】由题意得可得与的最大值的和为,结合和关于圆心中心对称即可求解.
【详解】解:∵
∴与的最小值为
∴与的最大值的和为
∵和关于圆心中心对称
∴
∴,最大值为
故选:B
3.D
【分析】取OA的中点Q,连接DQ,OD,CQ,根据条件可求得CQ长,再由垂径定理得出OD⊥AP,由直角三角形斜边中线等于斜边一半求得QD长,根据当C,Q,D三点共线时,CD长最大求解.
【详解】解:如图,取AO的中点Q,连接CQ,QD,OD,
∵C为的三等分点,
∴的度数为60°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵Q为OA的中点,
∴CQ⊥OA,∠OCQ=30°,
∴OQ= ,
由勾股定理可得,CQ= ,
∵D为AP的中点,
∴OD⊥AP,
∵Q为OA的中点,
∴DQ= ,
∴当D点CQ的延长线上时,即点C,Q,D三点共线时,CD长最大,最大值为 .
故选D
4.
【分析】作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,求出,证明是正三角形,可得,然后可得答案.
【详解】解:如图,作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,
∵N是弧的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴是正三角形,
∴,
又∵,
∴周长的最小值为,
故答案为:.
【题型1 由弧、弦、圆心角的关系判断结论正误】
1.如图,是的直径,点P是上一个动点(点P不与点A,B重合),在点P运动的过程中,对于如下结论:①的值为定值;②的度数为定值;③的度数始终等于度数的2倍;④若,则.正确的结论有( )
A.4个 B.3个 C.2个 D.1个
2.下列说法正确的个数有( )
①半圆是弧;
②面积相等的两个圆是等圆;
③所对的弦长相等的两条弧是等弧;
④如果圆心角相等,那么它们所对的弦一定相等;
⑤等弧所对的圆心角相等;
⑥平分弦的直径,平分这条弦所对的弧.
A.2个 B.3个 C.4个 D.5个
3.如图所示,在中,,那么( )
A. B. C. D.无法比较
4.平分锐角,以为圆心以任意长为半径画,分别交,,于A,B,C三点,以C为圆心,以长为半径画弧与相交于异于B点的点D,连接,.下列结论错误的是( )
A. B.若,则
C. D.
【题型2 利用弧、弦、圆心角的关系求线段长度】
1.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=6,则点O到弦AB的距离为( )
A.6 B.8 C.3 D.4
2.如图,在中,圆心角是的中点,作,与交于,则图中与相等的线段有 条.
3.如图,是⊙O的直径,点C为圆上一点,,D是弧的中点,与交于点E.若E是的中点,则的长为( )
A.5 B.3 C.2 D.1
4.如图,是直径,是弦,点E在弦上.D是的中点,,,若四边形为平行四边形,则的半径是( )
A. B. C. D.
【题型3 利用弧、弦、圆心角的关系求角度】
1.如图,是的直径,C是弧的中点,点D在弧上,的延长线交于点E,则等于( )
A. B. C. D.
2.如图,点A,B,C,D在上,,点B是弧的中点,则的度数是( )
A. B. C. D.
3.如图,以的半径为半径,自上的A点起,在圆上依次画弧截取点B,C,D,E,F.正方形EFGH的中心为,连接FA,,则 .
4.如图,在中,,截三边所得的弦长,则 度.
【题型4 利用弧、弦、圆心角的关系求弧的度数】
1.如图,已知是的两条直径,且,过点作交于点,则弧的度数为 .
2.如图,已知是的直径, ,,那么弧度数等于 .
3.如图,在中,,以点为圆心,长为半径的圆交于点,交于点,求弧DE的度数.
4.如图,点A.B.C在⊙O上,.弧AB的度数为 .
【题型5 利用弧、弦、圆心角的关系求面积】
1.如图,已知圆内接四边形中,对角线是的直径,,是的中点,则的面积是 .
2.如图,点,,,都在上,圆的半径为,且,,则该( )
A. B. C. D.
3.如图,以等边的一边为直径的半圆交于点,交于点,若,则阴影部分的面积是( )
A. B. C. D.
4.已知:是的直径,C为上一点,将绕着点B逆时针旋转一定的角度得到,交于E点,若点D在上,连接交于点F.
(1)直接判断与的位置关系;
(2)求证:;
(3)若,,求阴影部分的面积.
【题型6 利用弧、弦、圆心角的关系求周长】
1.如图所示,是半径为3的上的两点.若是的中点,则四边形的周长为 .
2.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4 cm,则⊙O的周长为 .
3.如图的弦,且于,连接,若,则的周长为( )
A. B. C. D.
4.如图,点是的八等分点.若,四边形的周长分别为a,b,则下列正确的是( )
A. B. C. D.a,b大小无法比较
【题型7 利用弧、弦、圆心角的关系求线段比值】
1.如图, 将上的 沿弦翻折交半径于点D, 再将沿 翻折交于点E, 连接. 若, 则 的值 .
2.如图,在中,点C是劣弧的中点,点P在劣弧上,且,于H,当,则 .
3.如图,、、、依次为一直线上个点,,为等腰直角三角形,且,过点、、,且弧的度数,则的值是 .
4.如图,等边内接于,D为边上一动点(不与A、C重合),连接并延长交边于E,将沿翻折为,边交于点,若的周长记为,的周长记为,则的值为 .
【题型8 利用弧、弦、圆心角的关系进行证明】
1.(1)如图①,过上一点作两条弦、,若,则平分,为什么?
(2)如图②,若点在内,过点的两条弦,相等,则平分吗?为什么?
(3)如图③,若点在外,过点作、,分别交于点,和,,且,则平分吗?为什么?
2.如图,、是的两条弦,与相交于点E,.
(1)求证:;
(2)连接 作直线求证:.
3.如图,四边形是的内接四边形,直径平分.
(1)求证:;
(2)过点A向圆外作,且,求证:四边形为平行四边形.
4.如图,以为直径的圆O中,点O为圆心,C为弧的中点,过点C作且.连接,分别交,于点E,F,与圆O交于点G,连接.
(1)求证:;
(2)连接,,求证:.
【题型9 利用弧、弦、圆心角的关系判断线段或弧长间的关系】
1.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是( )
A. B. C. D.不能确定
2.从圆内一点引两条弦与,则与、度数间的关系是 .
3.如图,圆上有A,B,C,D四点,圆内有E,F两点且点E,F在BC上.若四边形AEFD为正方形,则下列弧长关系中,正确的是( )
A. B. C. D.
4.将一张正方形的透明纸片ABCD和按如图位置叠放,顶点A、D在上,边AB、BC、CD分别与相交于点E、F、G、H,则下列弧长关系中正确的是( )
A. B.
C. D.
【题型10 利用弧、弦、圆心角的关系求最值】
1.如图,是半圆O的直径,半圆的半径为4,点C,D在半圆上,,点P是上的一个动点,则的最小值为 .
2.)如图1为某酒店的圆形旋转门,可看成如图2由外围的和3翼隔风玻璃组成,外围圆有通道和,且它们关于圆心中心对称,圆内的3翼隔风玻璃可绕圆心转动,且所成的夹角,3翼隔风玻璃在转动过程中,始终使大厅内外空气隔离,起到对大厅内保温作用.例如:当隔风玻璃转到如图2位置时,大厅内外空气被隔风玻璃,隔离.则通道所对圆心角的度数的最大值为( )
A.30° B.60° C.90° D.120°
3.如图,AB是O的直径,AB=4,C为的三等分点(更靠近A点),点P是O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
A.2 B. C. D.
4.如图,是的直径,,点M在上,,N是弧的中点,P是直径上的一动点.若,则周长的最小值为 .
参考答案
【题型1 由弧、弦、圆心角的关系判断结论正误】
1.C
【分析】本题考查主要考查了圆心角、弧、弦的关系,圆周角定理等知识,熟记圆中有关观念时解本题的关键.根据圆周角定理,圆心角,弧,弦之间的关系解决问题即可.
【详解】解:①由题可得:当点P从点A运动到的中点时,的值在增大,当点P从的中点运动到点B时,的值在减小,
故①错误;
②时直径,
,
的度数为定值,
②正确;
③,
,
,
的度数始终等于度数的2倍,
③正确;
④如图,取的中点,连接,,,则,
,
,
,
,
,
④错误;
正确的结论个数是2个,
故选:C
2.B
【分析】根据半圆的定义判断①;根据圆的面积公式和等圆的定义判断②;根据圆心角、弧、弦的关系判断③④⑤;根据垂径定理的推论判断⑥.
【详解】解:半圆是弧,故①正确;
面积相等的两个圆半径相等,因此是等圆,故②正确;
在同圆或等圆中,所对的弦长相等的两条劣弧是等弧,两条优弧是等弧,故③错误;
在同圆或等圆中,如果圆心角相等,那么它们所对的弦一定相等,故④错误;
等弧所对的圆心角相等,故⑤正确;
平分弦(非直径)的直径,平分这条弦所对的弧,故⑥错误;
综上可知,正确的有①②⑤,共3个,
故选B.
3.B
【分析】本题考查了圆心角、弧、弦之间的关系和三角形的三边关系,在圆上截取,再根据“根据三角形的三边关系”可解,熟练掌握圆心角、弧、弦之间的关系和三角形的三边关系是解题的关键.
【详解】解:如图,
在圆上截取,
∵,
∴,
∴,
根据三角形的三边关系知,,
∴,
故选:.
4.D
【分析】先根据题意画好图形,如图,连接,,由角平分线的定义结合圆心角,弧,弦之间的关系,判断A;证明为等边三角形,可判断B;连接,证明,可判断C;连接,可得,可判断D ,从而可得答案.
【详解】解:如图,连接,,
∵平分锐角,
∴,
∴,故A不符合题意;
∵由作图可得,
∴,
∴,
∵,,
∴为等边三角形,
∴,
∴,故B不符合题意;
连接,
∵,,
∴,
∴,故C不符合题意;
连接,
∵,,
∴,
∴,故D符合题意.
故选D.
【题型2 利用弧、弦、圆心角的关系求线段长度】
1.C
【分析】延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,根据垂径定理求出DH=HC=3,DF=EF,根据三角形的中位线求出DE=2OH,根据勾股定理求出OH长,再根据勾股定理求出OF长即可.
【详解】解:延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O到弦AB的距离,
∵∠COD和∠DOE互补,∠COD和∠AOB互补,
∴∠DOE=∠AOB,
∴DE=AB,OF=OG,
∵OH⊥DC,CD=6,OH过O,
∴DH=HC=DC=3,∠OHD=∠OHC=90°,
由勾股定理得:OH===4,
∵OC=OE,DH=HC,OH=4,
∴DE=2OH=8,
∵OF⊥DE,OF过O,
∴DF=EF=DE=4,
在Rt△DFO中,由勾股定理得:OF===3,
∴OG=OF=3,
即点O到AB的距离是3,
故选:C.
2.3
【分析】此题考查了圆心角、弧、弦的关系,等边三角形的性质与判定;连接,,根据圆心角、弧的关系求出,根据圆周角定理求出,根据直角三角形的性质求出,再根据等边三角形的判定与性质求解即可.
【详解】解:如图,连接,,
,是的中点,
,
,
,
,
,
,
是等边三角形,
,,
,,
是等边三角形,
,
,
图中与相等的线段有条,
故答案为:.
3.C
【分析】
连接交于F,由垂径定理得,,可证,接着证明得到,计算得,然后设,则,,最后利用勾股定理计算得到BC的长.
【详解】
解:连接交于F,如图,
D是弧的中点,
,
,
是直径,
,
,
,
E是的中点,
,
,
,
,
,
,
,
设,则,
,
在中,,
,
解得,
即,
故选:C.
4.B
【分析】等弧对等弦,得到,得到三角形为等腰三角形,圆周角定理得到,平行四边形的性质,得到,三线合一得到点为的中点,连接,中位线定理,得到,垂径定理得到,进而得到三点共线,即可得出的半径.
【详解】解:∵是直径,
∴,
∵D是的中点,
∴,
∴,
∵四边形为平行四边形,
∴,,
∴,
∴,
∵,
∴,
则:点为的中点,
连接,则:,,
∵,
∴三点共线,
∴;即的半径是.
故选B.
【题型3 利用弧、弦、圆心角的关系求角度】
1.B
【分析】由是的直径,则可得,已知C是弧的中点,则,根据圆周角定理可知,故,根据 即可解答.
【详解】解:∵是的直径,
∴,
∴,
∵C是弧的中点,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:B.
2.C
【分析】本题考查了同弧或等弧所对的圆心角相等,圆周角定理.熟练掌握同弧或等弧所对的圆心角相等,圆周角定理是解题的关键.
如图,连接,则,,由圆周角定理可得,计算求解即可.
【详解】解:如图,连接,
∵点B是弧的中点,
∴,
∴,
∵,
∴,
故选:C.
3.75°
【分析】连接OA,OF,OE,根据等边三角形的判定和性质,圆心角、弧、弦关系,求得∠AFE=120°,再根据正方形的性质求得∠O1FE=45°,计算角的差即可解答;
【详解】解:如图,连接OA,OF,OE,
∵FE=OF=OE,∴△OFE是等边三角形,∴∠OFE=60°,∴弧FE=60°,
由圆心角、弧、弦关系可得弧FE=弧ED=弧DC=弧CB=弧BA=60°,
∴弧AF=360°-60°×5=60°,∴∠AOF=60°,
∵OA=OF,∴△OAF是等边三角形,∴∠AFO=60°,
∴∠AFE=∠AFO+∠OFE=120°,
∵O1是正方形的中心,∴∠O1FE=45°,
∴∠AFO1=∠AFE -∠O1FE=75°,
故答案为:75°;
4.125
【分析】过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,由于=,利用弦、圆心角和对应的弦心距的关系得到OM=OK=OP,则可判断OA平分∠BAC,OC平分∠ACB,然后根据角平分线的定义和三角形内角和求解.
【详解】解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC+∠OCA=(∠BAC+∠ACB)=(180°∠B)=90° ,
∴∠AOC=180°(∠OAC+∠OCA)
=180°
=125°.
故答案为:125.
【题型4 利用弧、弦、圆心角的关系求弧的度数】
1.
【分析】本题考查平行线的性质,圆心角,弧,弦之间的关系,圆周角定理等知识点,
连接,根据平行线的性质求出,根据圆周角定理求出,再求出的度数,即可求出本题答案.
【详解】解:连接,
∵,,
∴,
∵,
∴
∴,
∴的度数是,
∵是的两条直径,
∴的度数是,
∴的度数是,
故答案为:.
2.
【分析】本题主要考了圆心角、弧、弦的关系.注意掌握数形结合思想的应用.
根据圆心角与弧的关系可求得的度数,从而即可求解.
【详解】∵
∴,
∴,
∴,
∴弧度数等于.
故答案为:.
3.
【分析】连接,如图,先根据等腰三角形的性质和三角形内角计算出,再利用得到,然后根据三角形外角性质计算出,从而得到弧的度数.
【详解】解:连接,如图,
∵,
∴,
∵,
∴,
∵,
∴,
∴弧的度数为.
4.
【分析】在⊙O中,和对着同一条弧,根据圆周角定理,可得出的度数,再根据弧与圆心角的关系即可得到答案.
【详解】解:在⊙O中,和对着同一条弧,
又,
,
因为弧的度数和它所对的圆心角的度数相等,
所以的度数为.
故答案为:.
【题型5 利用弧、弦、圆心角的关系求面积】
1.4
【分析】四边形ABCD是梯形,连接OB,则OBCD是菱形,即可求得AD的长,而△AED是等腰直角三角形,就可求得△ADE的面积.
【详解】解:连接EO,BO,CO
∵AB=BC=CD=2,
∴∠AOB=180÷3=60°,
∴△AOB是等边三角形,
那么OA=AB=2,那么AD=2OA=4.
∵E是的中点,
∴AE=DE,
∴EO⊥AD,
∵EO=2,
∴△ADE的面积=×4×2=4.
故答案为4
2.A
【分析】本题考查了圆周角定理,圆心角、 弧、 弦之间的关系,勾股定理.连接, 求出,求出是圆的直径,根据勾股定理求出,根据计算是解题的关键.
【详解】解:连接,
,
,,
,
即是圆的直径,
,
∵圆的半径为,
,
,
由勾股定理得:
,
∴,
故选:A.
3.A
【分析】连接,,,可得,,都是等边三角形,从而得弓形的面积弓形的面积,进而得阴影部分的面积的面积,进而即可求解.
【详解】连接,,,
是等边三角形,
,,
,
,,,都是等边三角形,
,
弓形的面积弓形的面积,
阴影部分的面积的面积,
,
是等边三角形,边长为,
过点作于点,则, ,
的面积 ,
阴影部分的面积 .
故选:A.
4.(1)解:
将绕着点B逆时针旋转一定的角度得到,交于E点,所以所在的圆与是等圆,连接
∴,
∴点B是中点,
∵是的直径,
∴;
(2)证明:连接,
∵,所在的圆与是等圆,
∴,
∴,
∵,
∴;
(3)解:由(2)得,,所在的圆与是等圆,
所以弓形和弓形的面积相等,阴影部分的面积就是三角形的面积,
连接,
∵,,
∴,
∴,
∴,
所以三角形的面积=,
阴影面积为:
【题型6 利用弧、弦、圆心角的关系求周长】
1.12
【分析】通过等弧所对的圆心角相等和,得到和都是等边三角形,再求出四边形的周长.
【详解】解:连接,
∵C是的中点,
∴,
∵,
∴,
∵,
∴和都是等边三角形,
∴,
∴四边形的周长等于为.
故答案为:.
2.8cm
【分析】如图,连接OD、OC.根据圆心角、弧、弦的关系证得△AOD是等边三角形,则⊙O的半径长为DA=4cm;然后由圆的周长公式进行计算.
【详解】解:如图,连接OD、OC.
∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,
∴,
∴∠AOD=∠DOC=∠BOC=60°.
又OA=OD,
∴△AOD是等边三角形,
∴OA=AD=4cm,
∴⊙O的周长=2×4π=8π(cm).
故答案为:8πcm.
3.A
【分析】连接AB、OA、OD,然后由弦与弧的关系,求出,得到,再根据勾股定理求出半径,即可得到答案.
【详解】解:连接AB、OA、OD,如图,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
在直角△AOD中,设OA=OD=R,
∵,
∵,
∴,
∴,
∴圆的周长为:;
故选:A.
4.A
【分析】连接,依题意得,,的周长为,四边形的周长为,故,根据的三边关系即可得解.
【详解】连接,
∵点是的八等分点,即
∴,
∴
又∵的周长为,
四边形的周长为,
∴
在中有
∴
故选A.
【题型7 利用弧、弦、圆心角的关系求线段比值】
1.
【分析】本题主要考查折叠的性质,等腰三角形的性质,圆周角定理及弧,弦,圆心角之间的关系,勾股定理.连接、、,作于F,设,则,,,先利用折叠的性质和圆周角定理得到 ,再利用弧、弦、圆心角的关系得到,然后利用勾股定理计算出,接着再计算出即可.
【详解】解:连接、、,作于F,如图所示,
设,则,,
∴,
∵上的沿弦翻折交半径于点D,再将沿 翻折交于点E,
∴为等圆中的弧,
∵它们所对的圆周角为,
∴,
∴,
∴,
∴,
在中,,
在中,,
,
∴.
故答案为:.
2.
【分析】在上截取,连接,可以证明,得到,由,得到,由圆周角定理得到,因此,得到,即可求解.
【详解】在上截取,连接,
∵C是的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴,
∴,
故答案为:.
3.
【分析】本题考查了等腰直角三角形的性质,弧与圆心角的关系,矩形的性质,勾股定理,正确作辅助线是解题关键;连接,延长交分别为,得到是等腰直角三角形,则四边形是矩形,是等腰直角三角形,设,则,进而表示出,根据勾股定理建立关系式,整理得出,即可求解.
【详解】如图所示,连接,延长交分别为,
∵,为等腰直角三角形
∴,
∵弧的度数,
∴是等腰直角三角形,
则四边形是矩形,是等腰直角三角形,
设,则,
∴,
在中,
∴
即
整理得,
∴
故答案为:.
4.
【分析】此题考查了折叠的性质,圆周定理,等边三角形的性质,连接,,延长交于点,连接,由折叠性质可知:,则,从而有,通过弧度和差可得,所以,再由周长即可求解.在同圆或等圆中,等弧所对的圆心角、弦相等,解题的关键是熟练掌握以上知识的应用.
【详解】如图,连接,,延长交于点,连接,
由折叠性质可知:,
∴,
∵,
∴,即,
∴,
∵是等边三角形,
∴,
∴,
∴,,
∴,
∴,
∴,
设,
∴的周长,
的周长,
∴,
故答案为:.
【题型8 利用弧、弦、圆心角的关系进行证明】
1.解:(1)平分,
如图,作直径,
,
,
,
,
平分;
(2)平分.理由如下:
作于,于,连接、,如图,
则,,
,
,
而,,
,
平分;
(3)平分.理由如下:
作于,于,连接、,如图,
则,,同理(2)可得,
平分.
2.(1)证明:∵,
∴
∴,
即.
∴.
(2)证明:连接
∵
∴
∴
∴
∵
∴E、O都在的垂直平分线上.
∴
3.(1)证明:为直径,
,
直径平分,
,
,
,
,
;
(2)证明:
四边形为平行四边形.
4.(1)证明:∵,,
∴四边形为平行四边形,
∵为半圆的中点,
∴,即,
∴平行四边形为矩形.
∴,
∴.
(2)证明:连接,,交于,
由(1)可知平行四边形为矩形,
∵,
∴四边形为正方形,则,,
∵,
∴,
∴,
∵,
∴,
∵,,
∴垂直平分,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
【题型9 利用弧、弦、圆心角的关系判断线段或弧长间的关系】
1.【分析】连接OC,BC,过O作OE⊥AC于D交圆O于E,根据折叠的性质得到ODOE,根据圆周角定理得到∠ACB=90°,根据三角形的中位线的性质得到ODBC,求得∠COB=60°,得到∠AOC=120°,于是得到结论.
【解答】解:如图,连接OC,BC,过O作OE⊥AC于D交圆O于E,
∵把半圆沿弦AC折叠,恰好经过点O,
∴ODOE,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴OD∥BC,
∵OA=OB,
∴ODBC,
∴BC=OE=OB=OC,
∴∠COB=60°,
∴∠AOC=120°,
∴,
故选:A.
2.(的度数 的度数)
【分析】本题考查了圆心角、弧、弦之间的转化,圆周角的度数等于它所对的弧的度数.连,根据三角形外角性质得到,而的度数,的度数,由此得到与、度数间的关系.
【详解】解:如图,连,
,
又的度数,的度数,
(的度数 的度数).
3.C
【分析】由图知,BC>AD,根据大弦对大弧知, .
【详解】A、因为四边形AEFD为正方形,所以AD=AE,则其所对的弧相等,因为AB>AE,所以,故A项不正确;
B、因为四边形AEFD为正方形,所以AD=AE,因为AB>AE,所以AB>AD,则可得 ,故B项不正确;
C、弦AB<AE+BE(三角形两边之和大于第三边),弦BC=EF+BE+FC>EF+BE=AE+BE>弦AB,所以,故C项正确;
D、由图可看出其不相等,故D项错误.
故答案选:C.
4.C
【分析】连接,根据弦与弧的关系,只要比较弦长即可比较弧长的大小即可求解.
【详解】如图,连接,过点作,交于,交于,则,
四边形是正方形,
,,
,
四边形是矩形,
,
,
,
,
,
A. , ,故该选项不正确,不符合题意;
B. ,,故该选项不正确,不符合题意;
C. , ,故该选项正确,符合题意;
D., ,故该选项不正确,不符合题意;
故选:C.
【题型10 利用弧、弦、圆心角的关系求最值】
1.
【分析】依题意,作点关于的对称点为,连接,长即为最小值;过点作,构造和进行对应线段求解;
【详解】作点关于的对称点为,连接,;过点作;
由题知,,,∴,可得对应的圆心角;
又点关于的对称点为,
∴,,∴长为的最小值
在中,,∴,;
在中,,,∴;
故填:;
2.B
【分析】由题意得可得与的最大值的和为,结合和关于圆心中心对称即可求解.
【详解】解:∵
∴与的最小值为
∴与的最大值的和为
∵和关于圆心中心对称
∴
∴,最大值为
故选:B
3.D
【分析】取OA的中点Q,连接DQ,OD,CQ,根据条件可求得CQ长,再由垂径定理得出OD⊥AP,由直角三角形斜边中线等于斜边一半求得QD长,根据当C,Q,D三点共线时,CD长最大求解.
【详解】解:如图,取AO的中点Q,连接CQ,QD,OD,
∵C为的三等分点,
∴的度数为60°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵Q为OA的中点,
∴CQ⊥OA,∠OCQ=30°,
∴OQ= ,
由勾股定理可得,CQ= ,
∵D为AP的中点,
∴OD⊥AP,
∵Q为OA的中点,
∴DQ= ,
∴当D点CQ的延长线上时,即点C,Q,D三点共线时,CD长最大,最大值为 .
故选D
4.
【分析】作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,求出,证明是正三角形,可得,然后可得答案.
【详解】解:如图,作点N关于的对称点,则点在上,连接交于P,此时的值最小,最小值为的长,连接,,,
∵N是弧的中点,
∴,
∵,
∴,
∴,
∴,
∵,
∴是正三角形,
∴,
又∵,
∴周长的最小值为,
故答案为:.
