【期中押题卷】上海市2024-2025学年六年级下学期期中综合测试数学试卷沪教版(含解析)
文档属性
| 名称 | 【期中押题卷】上海市2024-2025学年六年级下学期期中综合测试数学试卷沪教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 721.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-04 00:00:00 | ||
图片预览




文档简介
上海市2024-2025学年六年级下学期期中综合测试数学试卷
一.填空题(共13小题,满分27分)
1.(2分)(2023春 澄迈县月考)在第一次检测中,六(1)班数学科的平均分是88分。如果以平均分为标准,张强和李远的成绩分别是﹣2和6,则他们的实际成绩分别是 分和 分。
2.(4分)(2023 徐闻县)0.25= ÷ =9: = %
3.(2分)如果5m=7n(m≠0,n≠0),那么m和n成 比例;如果(y≠0),那么x和y成 比例。
4.(1分)(2022 岷县模拟)已知比例的两个内项的积是,一个外项是两个内项积的倒数,另一个外项是 。
5.(2分)(2021 龙港区)三角形的面积一定,底和高成 比例;工作时间一定,工作总量和工作效率成 比例。
6.(3分)(2023 奈曼旗)国家出台了建设新农村的政策,我的家乡也已经开始进行街道规划了,街道规划平面图上标的比例尺是它表示 。把它写成数值比例尺的形式是 。在这幅地图上从政府大楼到我家的距离是7cm,那么我家到政府大楼的实际距离是 。
A、图上的1cm的距离相当于实际的100km
B、图上的1cm的距离相当于实际的50km
C、1:5000000
D、1:10000000
E、350km
F、700km
7.(2分)(2023春 松江区期中)60平方分米= 平方米
4.25立方米= 立方分米
8.(3分)(2022秋 郏县期末)
0.25立方米= 升 升= 毫升 40分= 时
9.(3分)如图,把底面半径3cm,高10cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的底面积是 cm2,表面积是 cm2,体积是 cm3。
10.(1分)(2021秋 迎江区期末)被减数、减数与差三个数的和是72,差与减数的比4:5,差是 ,减数是 。
11.(1分)把一个圆柱的侧面展开后得到一个正方形,若圆柱的底面直径是4cm,则圆柱的高是 cm。
12.(1分)(2021春 邱县期中)用36个完全一样的圆锥形铁坯,可以铸成 个与圆锥等底等高的圆柱。
13.(2分)(2023春 灵山县期中)将一个圆柱沿直径切开,得到两个边长是16厘米的正方形切面。原来圆柱的表面积是 平方厘米,体积是 立方厘米。
二.选择题(共6小题,满分6分,每小题1分)
14.(1分)(2024 襄城县)如图,b对应的数最有可能是( )
A.0 B.﹣3 C.+2 D.﹣1
15.(1分)(2021 河东区)比例的两个外项分别是2和5,下面列出的比例正确的是( )
A.2:5=1:2.5 B.2.5:2=5:4 C.2:2.5=4:5 D.5:4=3:2
16.(1分)张师傅加工一个零件需要小时,李师傅加工相同的一个零件需要小时,张师傅与李师傅的工作效率之比为( )
A.2:3 B.3:2 C.2:5
17.(1分)(2020秋 定兴县期末)根据3M=5N(M,N均不为0)可以写成不同的比例,下面比例式正确的是( )
A.M:N=3:5 B.M:3=5:N C.5:3=M:N D.M:3=N:5
18.(1分)(2022春 新晃县期中)一个圆柱和一个圆锥等底等高,它们的体积之和是52dm3,那么这个圆柱的体积是( )dm3。
A.13 B.26 C.39
19.(1分)(2022春 电白区期中)如图,把一个底面周长是18.84厘米、高是5厘米的圆柱体横截成二段,表面积增加( )平方厘米。
A.141.3 B.56.52 C.94.2
三.判断题(共6小题,满分6分,每小题1分)
20.(1分)(2023 永寿县)长方形的长一定,长方形的面积和宽成正比例。
21.(1分)(2022 即墨区)圆的周长和它的半径成反比例关系。
22.(1分)(2024 茌平区)比例的一个外项扩大到原来的2倍,一个内项缩小到原来的,比例仍然成立。
23.(1分)(2021春 蓝田县期中)一个圆柱的侧面积是376.8dm2,底面半径是2dm,这它的高是60dm。
24.(1分)(2023 赞皇县)当圆柱、正方体、长方体的底面周长相等,高也相等时,圆柱的体积最大。
25.(1分)(2022 杭州模拟)用20个小正方体搭一个长方体,不管怎样搭,体积都相等。
四.计算题(共2小题,满分16分)
26.(6分)
3.53+47= 125×16= 7.2÷0.05÷20= 3.9×30%= 9.6÷0.6=
3.3×4.9+5.1×3.3= 0.72÷3.6= 0.77+0.33= (15.4﹣0.4)×4= 0.7﹣0.08=
0.27×0.7= 0.53×5+0.47×5= 300÷2.5= 0.25+7.85= 6.4+2.5×4=
45= 7.2÷0.4=
54.8%﹣39.9%= 24=
(
83%﹣38%= 0.36÷36%= 3.85﹣1.36﹣1.64= 2.68÷0.04= 5.61﹣1.1=
27.(10分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
五.操作题(共3小题,满分14分)
28.(4分)(2023秋 天河区期末)请你在方格纸上画一个长4厘米、宽2厘米的长方形,再算一算,要画一个与这个长方形周长相等的正方形,它的边长是 厘米。
29.(4分)(2024 邳州市模拟)如图是某地区的平面示意图。
(1)中原桃花岛位于汇龙国际 偏 °方向 米处。
(2)文景苑位于汇龙国际正西100米处,请在图中标出它的位置。
(3)文苑路位于解放路北侧100米,并与解放路平行,在图中用线表示出来。
30.(6分)(2024秋 惠济区期末)市政府准备在圆形喷水池附近修建一个周长是30米的长方形花坛,使它的长与宽的比是2:1,请你在如图画出长方形花坛的示意图。(每个小方格的边长表示1米)
六.解答题(共5小题,满分31分)
31.(6分)小明想知道学校旗杆的高度,他的方法是,选择一根竹竿,把1.8米长的竹竿直立在旗杆旁,量得它的影长是1.5米,同时量得学校旗杆的影长是6米,现在你能算出旗杆的高度吗?(用比例解)
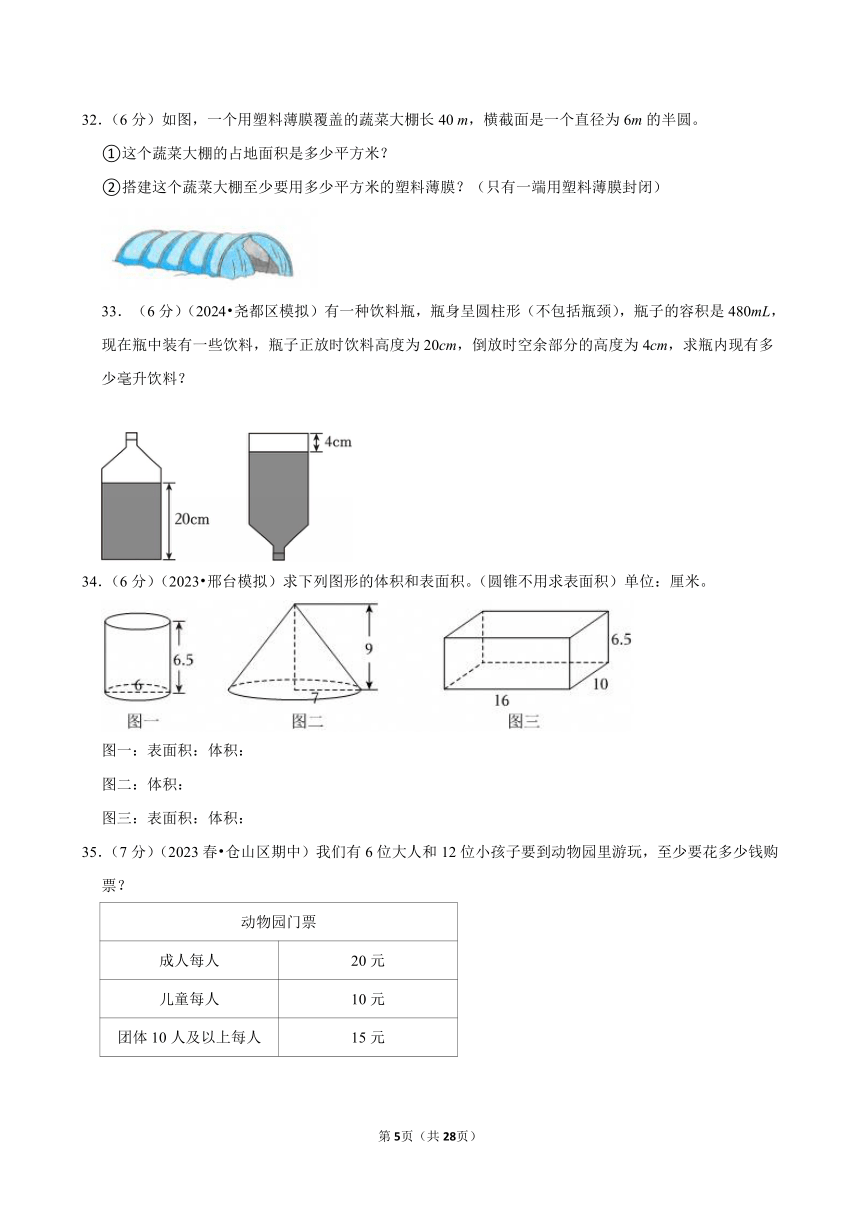
32.(6分)如图,一个用塑料薄膜覆盖的蔬菜大棚长40 m,横截面是一个直径为6m的半圆。
①这个蔬菜大棚的占地面积是多少平方米?
②搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(只有一端用塑料薄膜封闭)
(6分)(2024 尧都区模拟)有一种饮料瓶,瓶身呈圆柱形(不包括瓶颈),瓶子的容积是480mL,现在瓶中装有一些饮料,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,求瓶内现有多少毫升饮料?
34.(6分)(2023 邢台模拟)求下列图形的体积和表面积。(圆锥不用求表面积)单位:厘米。
图一:表面积:体积:
图二:体积:
图三:表面积:体积:
35.(7分)(2023春 仓山区期中)我们有6位大人和12位小孩子要到动物园里游玩,至少要花多少钱购票?
动物园门票
成人每人 20元
儿童每人 10元
团体10人及以上每人 15元
上海市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.填空题(共13小题,满分27分)
1.(2分)(2023春 澄迈县月考)在第一次检测中,六(1)班数学科的平均分是88分。如果以平均分为标准,张强和李远的成绩分别是﹣2和6,则他们的实际成绩分别是 86 分和 94 分。
【考点】负数的意义及其应用.
【专题】综合填空题;数感.
【答案】86,94。
【分析】以平均分为标准,﹣2表示比平均分少2分,6表示比平均分多6分,据此计算他们的实际成绩。
【解答】解:以平均分88分为标准,张强的成绩是﹣2,就是比88分少2分,他的实际成绩是86分,李远的成绩是6,就是比88分多6分,他的实际成绩是94分。
故答案为:86,94。
【点评】此题主要考查正负数的意义。
2.(4分)(2023 徐闻县)0.25= 1 ÷ 4 =9: 36 = 25 %
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化.
【专题】综合填空题;数据分析观念.
【答案】1;4;36;25。
【分析】小数化成除法算式,0.25=1÷4;由分除法算式转化成比,根据比的基本性质,比的前项和后项同时乘或除以相同的数,(0除外)比值不变,最后由小数转化成百分数,将小数乘100,得到25,然后在后面加上百分号,即25%。
【解答】解:0.25=1÷4=(1×9):(4×9)=9:36
0.25=25%
则0.25=1÷4=9÷36=25%。
故答案为:1;4;36;25。
【点评】此题考查了小数、除法算式和百分数之间的互化,要求学生掌握。
3.(2分)如果5m=7n(m≠0,n≠0),那么m和n成 正 比例;如果(y≠0),那么x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】正,反。
【分析】两个相关联的量,如果它们的乘积一定,则这两个量成反比例,如果它们的比值一定,则这两个量成正比例;先根据两个关系式推出m和n、x和y相乘或相除等于一个不变的量,从而再进行判断。
【解答】解:如果5m=7n(m≠0,n≠0),变式为,那么m和n成正比例;
如果(y≠0),变式为xy=30,那么x和y成反比例。
故答案为:正,反。
【点评】本题考查的是正、反比例的认识,关键是掌握什么叫正、反比例。
4.(1分)(2022 岷县模拟)已知比例的两个内项的积是,一个外项是两个内项积的倒数,另一个外项是 。
【考点】比例的意义和基本性质.
【专题】常规题型;能力层次.
【答案】。
【分析】依据比例的基本性质,即两内项之积等于两外项之积,已知比例内项之积是,那么两外项的积也是,其中一个外项是内项之积的倒数,即其中一个外项是(1),(1)即可求出另一个外项。
【解答】解:1
答:另一个外项是。
故答案为:。
【点评】解答此题的主要依据是:比例的基本性质以及倒数的求法。
5.(2分)(2021 龙港区)三角形的面积一定,底和高成 反 比例;工作时间一定,工作总量和工作效率成 正 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】反,正。
【分析】底×高=三角形的面积×2,工作总量÷工作效率=工作时间。据此解答。
【解答】解:三角形的面积一定,底和高成反比例;工作时间一定,工作总量和工作效率成正比例。
故答案为:反,正。
【点评】两个相关联的量,若它们的比值一定,这两个量成正比例关系;若它们的乘积一定,这两个量成反比例关系。
6.(3分)(2023 奈曼旗)国家出台了建设新农村的政策,我的家乡也已经开始进行街道规划了,街道规划平面图上标的比例尺是它表示 B 。把它写成数值比例尺的形式是 C 。在这幅地图上从政府大楼到我家的距离是7cm,那么我家到政府大楼的实际距离是 E 。
A、图上的1cm的距离相当于实际的100km
B、图上的1cm的距离相当于实际的50km
C、1:5000000
D、1:10000000
E、350km
F、700km
【考点】比例尺;图上距离与实际距离的换算(比例尺的应用).
【专题】比和比例;应用意识.
【答案】B、C、E。
【分析】根据线段比例尺的意义,可知这个街道规划平面图上标的比例尺中图上1厘米相当于实际50千米;再根据比例尺=图上距离:实际距离,把线段比例尺改写成数值比例尺;最后根据图上1厘米相当于实际50千米,则图上7厘米就相当于实际7个50千米,用乘法求出我家到政府大楼的实际距离。
【解答】解:(1)街道规划平面图上标的比例尺表示图上1厘米相当于实际50千米;
(2)写成数值比例尺是:1厘米:50千米
=1厘米:5000000厘米
=1:5000000
(3)50×7=350(千米)
故答案为:B、C、E。
【点评】本题考查比例尺的意义以及应用。关键是区分线段比例尺、数值比例尺的意义,并能熟练应用。
7.(2分)(2023春 松江区期中)60平方分米= 0.6 平方米
4.25立方米= 4250 立方分米
【考点】小面积单位间的进率及单位换算;体积、容积进率及单位换算.
【专题】常见的量.
【答案】0.6;4250。
【分析】根据1平方米=100平方分米,1立方米=1000立方分米,解答此题即可。
【解答】解:60平方分米=0.6平方米
4.25立方米=4250立方分米
故答案为:0.6;4250。
【点评】熟练掌握面积单位、体积单位的换算,是解答此题的关键。
8.(3分)(2022秋 郏县期末)
0.25立方米= 250 升 升= 600 毫升 40分= 时
【考点】体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算.
【专题】长度、面积、体积单位;质量、时间、人民币单位;数据分析观念.
【答案】250,600,。
【分析】1立方米=1000立方分米=1000升,1立方分米=1升=1000立方厘米,1时=60秒分,利用单位之间的换算的方法:大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率,据此解答。
【解答】解:
0.25立方米=250升 升=600毫升 40分时
故答案为:250,600,。
【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
9.(3分)如图,把底面半径3cm,高10cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的底面积是 28.26 cm2,表面积是 304.92 cm2,体积是 282.6 cm3。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;几何直观.
【答案】28.26、304.92、282.6。
【分析】依据题意结合图示可知,长方体的底面积等于圆柱的底面积,表面积等于圆柱的表面积加上2个长是10厘米,宽是3厘米的长方形的面积,体积等于圆柱的体积,由此解答本题。
【解答】解:3.14×3×3
=3.14×9
=28.26(cm2)
28.26×2+3.14×3×2×10+2×10×3
=56.52+188.4+60
=304.92(cm2)
3.14×3×3×10
=3.14×90
=282.6(cm3)
答:这个长方体的底面积是28.26cm2,表面积是304.92cm2,体积是282.6cm3。
故答案为:28.26、304.92、282.6。
【点评】本题考查的是圆柱的表面积、体积公式的应用。
10.(1分)(2021秋 迎江区期末)被减数、减数与差三个数的和是72,差与减数的比4:5,差是 16 ,减数是 20 。
【考点】按比例分配应用题.
【专题】运算能力.
【答案】16,20。
【分析】因为被减数=减数+差,因此被减数、减数、差三个数的和等于减数与差之和的2倍,因此减数与差之和是72÷2=36,然后根据减数与差的比,用按比例分配的方法解决问题。
【解答】解:72÷2=36
3616
3620
答:差是16,减数是20。
故答案为:16,20。
【点评】此题解答的关键在于根据被减数、减数、差之间的关系,求出减数与差二者之和,进而解决问题。
11.(1分)把一个圆柱的侧面展开后得到一个正方形,若圆柱的底面直径是4cm,则圆柱的高是 12.56 cm。
【考点】圆柱的展开图.
【专题】平面图形的认识与计算;空间观念.
【答案】12.56。
【分析】因为圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于圆柱的高,由此根据圆的周长公式C=πd,求出圆柱的底面周长,即圆柱的高。
【解答】解:3.14×4=12.56(厘米)
答:圆柱的高是12.56厘米。
故答案为:12.56。
【点评】此题主要考查了圆柱的侧面展开图与圆柱的关系,如果圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于圆柱的高。
12.(1分)(2021春 邱县期中)用36个完全一样的圆锥形铁坯,可以铸成 12 个与圆锥等底等高的圆柱。
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】12。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以3个圆锥形钢材可以熔铸成一个与它等底等高的圆柱。
【解答】解:36÷3=12(个)
答:可以铸成12个与圆锥等底等高的圆柱。
故答案为:12。
【点评】解答此题的依据是圆锥体积是与它等底等高的圆柱体积的。
13.(2分)(2023春 灵山县期中)将一个圆柱沿直径切开,得到两个边长是16厘米的正方形切面。原来圆柱的表面积是 1205.76 平方厘米,体积是 3215.36 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】1205.76,3215.36。
【分析】根据题意可知,把这个圆柱沿着底面直径并垂直于底面切开,若切面是边长16厘米的正方形,由此可知,这个圆柱的底面直径和高都是16厘米,圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×16×16+3.14×(16÷2)2×2
=3.14×256+3.14×64×2
=3.14×384
=1205.76(平方厘米)
3.14×(16÷2)2×16
=3.14×64×16
=200.96×16
=3215.36(立方厘米)
答:原来圆柱的表面积是1205.76平方厘米,体积是3215.36立方厘米。
故答案为:1205.76,3215.36。
【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是熟记公式。
二.选择题(共6小题,满分6分,每小题1分)
14.(1分)(2024 襄城县)如图,b对应的数最有可能是( )
A.0 B.﹣3 C.+2 D.﹣1
【考点】数轴的认识.
【专题】数感.
【答案】D
【分析】根据数轴的认识,将﹣2到3之间平均分成5段,b占其中的一点,靠近﹣2,所以为﹣1,据此解答即可。
【解答】解:如图:
b对应的数最有可能是﹣1。
故选:D。
【点评】本题考查数轴的认识。
15.(1分)(2021 河东区)比例的两个外项分别是2和5,下面列出的比例正确的是( )
A.2:5=1:2.5 B.2.5:2=5:4 C.2:2.5=4:5 D.5:4=3:2
【考点】比例的意义和基本性质.
【专题】推理能力.
【答案】C
【分析】组成比例的四个数叫做比例的项,中间的两个数叫做比例的内项,两端的两个数叫做比例的外项。据此选择即可。
【解答】解:AB中比例的两个外项不是2和5,不符合题意。
C.比例的两个外项不是2和5,并且2×5=2.5×4=10,符合题意。
D.5:4=1.25,3:2=1.5,1.25≠1.5,式子本身不成立,不符合题意。
故选:C。
【点评】此题主要是考查了比例的意义,学生需熟练掌握。
16.(1分)张师傅加工一个零件需要小时,李师傅加工相同的一个零件需要小时,张师傅与李师傅的工作效率之比为( )
A.2:3 B.3:2 C.2:5
【考点】比的意义;简单的工程问题.
【专题】运算能力.
【答案】A
【分析】由于完成相同的工作量,所用时间与工作效率成反比,则张师傅和李师傅工作效率的比是:。
【解答】解::2:3
答:张师傅与李师傅的工作效率的比为2:3。
故选:A。
【点评】本题是一道有关比的认识、简单的工程问题的题目,完成相同的工作量,用的时间越短,效率越高。
17.(1分)(2020秋 定兴县期末)根据3M=5N(M,N均不为0)可以写成不同的比例,下面比例式正确的是( )
A.M:N=3:5 B.M:3=5:N C.5:3=M:N D.M:3=N:5
【考点】比例的意义和基本性质.
【专题】比和比例;推理能力.
【答案】C
【分析】比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,据此把等式3M=5N看作两外项或两内项的积,转换成比例式即可。
【解答】解:因为3M=5N,所以M:N=5:3,也就是5:3=M:N。
故选:C。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
18.(1分)(2022春 新晃县期中)一个圆柱和一个圆锥等底等高,它们的体积之和是52dm3,那么这个圆柱的体积是( )dm3。
A.13 B.26 C.39
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;空间观念.
【答案】C
【分析】因为等底等高的圆锥的体积是圆柱体积的,所以等底等高的圆柱与圆锥的体积和相当于圆柱体积的(1),然后用除法解答即可。
【解答】解:52÷(1)
=39(立方分米)
答:圆柱的体积是39立方分米。
故选:C。
【点评】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用。
19.(1分)(2022春 电白区期中)如图,把一个底面周长是18.84厘米、高是5厘米的圆柱体横截成二段,表面积增加( )平方厘米。
A.141.3 B.56.52 C.94.2
【考点】圆柱的侧面积、表面积和体积.
【专题】几何直观.
【答案】B
【分析】如果把它切割成2段,表面积增加的是2个圆柱的底面积,由此利用面积公式S=πr2进行解答。先求出一个底面的面积,再乘2,即可求出表面积增加多少平方厘米。
【解答】解:18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
28.26×2=56.52(平方厘米)
答:表面积增加56.52平方厘米。
故选:B。
【点评】本题考查圆柱底面积的计算,熟练掌握公式是解决本题的关键。
三.判断题(共6小题,满分6分,每小题1分)
20.(1分)(2023 永寿县)长方形的长一定,长方形的面积和宽成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;运算能力.
【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答即可。
【解答】解:因为长方形的面积÷宽=长方形的长(一定),是商一定,所以长方形的长一定,长方形的面积与宽成正比例;所以原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.(1分)(2022 即墨区)圆的周长和它的半径成反比例关系。 ×
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:圆的周长÷半径=2π(一定),是比值一定,所以圆的周长和它的半径成正比例关系,所以本题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22.(1分)(2024 茌平区)比例的一个外项扩大到原来的2倍,一个内项缩小到原来的,比例仍然成立。 ×
【考点】比例的意义和基本性质.
【专题】比和比例;推理能力.
【答案】×
【分析】在比例里,一个外项扩大原来的2倍,要使比例照样成立,另一个外项要缩小到原来的;也可以使其中一个内项扩大原来的2倍;此题也可采用举例验证的方法解决。
【解答】解:根据分析可知,比例的一个外项扩大到原来的2倍,一个外项缩小到原来的,比例仍然成立。原题说法错误。
故答案为:×。
【点评】此题考查比例基本性质的运用:在比例里,两个内项的积等于两个外项的积。
23.(1分)(2021春 蓝田县期中)一个圆柱的侧面积是376.8dm2,底面半径是2dm,这它的高是60dm。 ×
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】要求这个圆柱体的高是多少分米,先要计算出圆柱的底面周长,根据圆柱的底面周长计算公式“C=2πr”,代入数值,计算出底面周长;然后根据“圆柱的高=侧面积÷底面周长”代入数字,进行解答即可。
【解答】解:376.8÷(2×3.14×2)
=376.8÷12.56
=30(dm)
答:它的高是30dm。
故答案为:×。
【点评】本题主要考查圆柱体侧面积计算公式的应用,此类题解答时应明确圆柱的底面周长和底面半径的关系,然后根据圆柱的侧面积、底面周长和高之间的关系进行分析解答即可得出结论。
24.(1分)(2023 赞皇县)当圆柱、正方体、长方体的底面周长相等,高也相等时,圆柱的体积最大。 √
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】√
【分析】根据圆的周长公式:C=2πr,正方形的周长公式:C=4a,长方形的周长公式:C=(a+b)×2,因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大,再根据圆柱、正方体、长方体的统一体积公式:V=Sh,所以圆柱、正方体和长方体的底面周长相等,高也相等时,圆柱的体积最大。据此解答即可。
【解答】解:因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大,再根据圆柱、正方体、长方体的统一体积公式:V=Sh,所以圆柱、正方体和长方体的底面周长相等,高也相等时,圆柱的体积最大。原题说法正确。
故答案为:√。
【点评】解答此题的关键是明确:因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大。
25.(1分)(2022 杭州模拟)用20个小正方体搭一个长方体,不管怎样搭,体积都相等。 √
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】√
【分析】由于长方体都是由20个小正方体搭成的,所以体积不变,由此求解。
【解答】解:无论怎么搭,搭成的长方体都是20个小正方体的体积和,所以体积不变。故题干说法正确。
故答案为:√。
【点评】本题考查了对体积的认识,明确小正方体的个数不变,搭成的体积不变。
四.计算题(共2小题,满分16分)
26.(6分)
3.53+47= 125×16= 7.2÷0.05÷20= 3.9×30%= 9.6÷0.6=
3.3×4.9+5.1×3.3= 0.72÷3.6= 0.77+0.33= (15.4﹣0.4)×4= 0.7﹣0.08=
0.27×0.7= 0.53×5+0.47×5= 300÷2.5= 0.25+7.85= 6.4+2.5×4=
45= 7.2÷0.4=
54.8%﹣39.9%= 24=
(
83%﹣38%= 0.36÷36%= 3.85﹣1.36﹣1.64= 2.68÷0.04= 5.61﹣1.1=
【考点】分数的四则混合运算;小数的加法和减法;小数乘法;小数除法.
【专题】运算能力.
【答案】50.53,2000,7.2,1.17,16,33,0.2,1.1,60,0.62,0.189,5,120,8.1,16.4,,35,,,18,2,,0.149,,,,,,,2,0.45,1,0.85,67,4.51,5。
【分析】根据整数、分数、小数、百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
3.53+47=50.53 125×16=2000 7.2÷0.05÷20=7.2 3.9×30%=1.17 9.6÷0.6=16
3.3×4.9+5.1×3.3=33 0.72÷3.6=0.2 0.77+0.33=1.1 (15.4﹣0.4)×4=60 0.7﹣0.08=0.62
0.27×0.7=0.189 0.53×5+0.47×5=5 300÷2.5=120 0.25+7.85=8.1 6.4+2.5×4=16.4
45=35 7.2÷0.4=18
2 54.8%﹣39.9%=0.149 24
(2
83%﹣38%=0.45 0.36÷36%=1 3.85﹣1.36﹣1.64=0.85 2.68÷0.04=67 5.61﹣1.1=4.51
5
【点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
27.(10分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
【考点】分数方程求解;解比例.
【专题】简易方程;运算能力.
【答案】x=11,x,x=7。
【分析】(1)根据等式的性质可得x,接下来对方程两边同时除以,求出x的值,即可解答;
(2)根据比例的性质可得(3﹣x)=4x×0.75,接下来根据等式的性质进行求解,即可解答;
(3)根据比例的性质可得6×(x﹣2)=5×(x﹣1),接下来根据等式的性质进行求解,即可解答。
【解答】解:1xx﹣2
x
x=11
4x:(3﹣x):0.75
(3﹣x)=4x×0.75
1x=3x
x=1
1
x
6(x﹣2)=5(x﹣1)
6x﹣12=5x﹣5
6x﹣5x=12﹣5
x=7
【点评】本题是一道关于解方程与解比例的题目,解答本题的关键是掌握等式的性质与比例的性质。
五.操作题(共3小题,满分14分)
28.(4分)(2023秋 天河区期末)请你在方格纸上画一个长4厘米、宽2厘米的长方形,再算一算,要画一个与这个长方形周长相等的正方形,它的边长是 3 厘米。
【考点】画指定长、宽(边长)的长方形、正方形.
【专题】平面图形的认识与计算;几何直观.
【答案】
【分析】根据题意,长方形的周长=(长+宽)×2,正方形的周长=边长×4,那么先画一个长厘米4厘米,宽2厘米的长方形,周长为12厘米的正方形的边长可为3厘米。
【解答】解:正方形的边长:
(4+2)×2÷4
=6×2÷4
=12÷4
=3(厘米)
作图如下:
【点评】此题主要考查的是如何根据周长确定正方形的边长,然后再作图即可。
29.(4分)(2024 邳州市模拟)如图是某地区的平面示意图。
(1)中原桃花岛位于汇龙国际 东 偏 南60 °方向 200 米处。
(2)文景苑位于汇龙国际正西100米处,请在图中标出它的位置。
(3)文苑路位于解放路北侧100米,并与解放路平行,在图中用线表示出来。
【考点】在平面图上标出物体的位置;根据方向和距离确定物体的位置.
【专题】图形与位置;应用意识.
【答案】(1)东,南60,200;(2)、(3)。
【分析】(1)根据上北下南左西右东的方向以及距离和角度,即可解答;
(2)根据上北下南左西右东的方向以及距离,即可解答;
(3)根据上北下南左西右东的方向以及距离作解放路平行线,即可解答。
【解答】解:(1)10000×2=20000(厘米)
20000厘米=200米
答:中原桃花岛位于汇龙国际东偏南60°方向200米处。
(2)、(3)100米=10000厘米
10000÷10000=1(厘米)
(2)、(3)作图如下:
故答案为:东,南60,200。
【点评】本题考查的是在平面上标出物体的位置,掌握上北下南左西右东的方向是解答关键。
30.(6分)(2024秋 惠济区期末)市政府准备在圆形喷水池附近修建一个周长是30米的长方形花坛,使它的长与宽的比是2:1,请你在如图画出长方形花坛的示意图。(每个小方格的边长表示1米)
【考点】比的应用;长方形的周长.
【专题】几何直观;应用意识.
【答案】
【分析】长方形周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数=一份数,一份数分别乘长和宽的对应份数,求出长和宽,作图即可。
【解答】解:30÷2=15(米)
15÷(2+1)
=15÷3
=5(米)
5×2=10(米)
5×1=5(米)
画出的长方形花坛长10米,宽5米,作图如下:
【点评】本题主要考查比的应用以及周长的周长公式。
六.解答题(共5小题,满分31分)
31.(6分)小明想知道学校旗杆的高度,他的方法是,选择一根竹竿,把1.8米长的竹竿直立在旗杆旁,量得它的影长是1.5米,同时量得学校旗杆的影长是6米,现在你能算出旗杆的高度吗?(用比例解)
【考点】正、反比例应用题.
【专题】比和比例应用题;应用意识.
【答案】7.2米。
【分析】由题可知,同一时刻物体的长度与影长成正比例据此列出比例解答即可。
【解答】解:设学校的旗杆高为x米。
1.8:1.5=x:6
1.5x=1.8×6
1.5x=10.8
x=7.2
答:学校的旗杆高7.2米。
【点评】本题是一道有关正、反比例的应用的题目,掌握正比例的判断方法是解题的关键。
32.(6分)如图,一个用塑料薄膜覆盖的蔬菜大棚长40 m,横截面是一个直径为6m的半圆。
①这个蔬菜大棚的占地面积是多少平方米?
②搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(只有一端用塑料薄膜封闭)
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】①240平方米:②390.93平方米。
【分析】①蔬菜大棚的占地面积即长为40m、宽为6m的长方形的面积。
②至少需要塑料薄膜的面积=直径为6m的圆面积的一半+圆柱侧面积的一半。
【解答】解:①6×40=240(m2)
答:这个蔬菜大棚的占地面积是240平方米。
②3.14×(6÷2)2÷2+3.14×6÷2×40
=14.13+9.42×40
=14.13+376.8
=390.93(m2)
答:搭建这个蔬菜大棚至少要用390.93平方米的塑料薄膜。
【点评】本题考查的是圆柱的应用题,熟记圆柱的底面积、侧面积、表面积公式是解答关键。
33.(6分)(2024 尧都区模拟)有一种饮料瓶,瓶身呈圆柱形(不包括瓶颈),瓶子的容积是480mL,现在瓶中装有一些饮料,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,求瓶内现有多少毫升饮料?
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】400毫升。
【分析】根据题意,瓶子的容积是480mL,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,瓶子的容积相当于高是(20+4)的圆柱的容积,所以底面积是480÷(20+4)=20(平方厘米),所以瓶内现有饮料体积=20×20=400(毫升),据此解答。
【解答】解:480÷(20+4)
=480÷24
=20(cm2)
20×20=400(mL)
答:瓶内现有400毫升饮料。
【点评】本题考查了圆柱的体积的相关知识,解决本题的关键是求出圆柱的底面积。
34.(6分)(2023 邢台模拟)求下列图形的体积和表面积。(圆锥不用求表面积)单位:厘米。
图一:表面积:体积:
图二:体积:
图三:表面积:体积:
【考点】圆柱的侧面积、表面积和体积;圆锥的体积;长方体和正方体的表面积;长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】图一:178.98平方厘米;183.69立方厘米;图二:461.58立方厘米;图三:658平方厘米;1040立方厘米。
【分析】图一:首先求出圆柱的底面半径,圆柱的体积=πr2h,圆柱表面积=2πr2+2πrh,代入数据计算即可解答。
图二:圆锥体积πr2h,代入数据计算即可解答。
图三:长方体体积=长×宽×高,长方体表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可解答。
【解答】解:图一:6÷2=3(厘米)
3.14×6×6.5
=18.84×6.5
=122.46(平方厘米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方厘米)
122.46+56.52=178.98(平方厘米)
3.14×32×6.5
=3.14×9×6.5
=28.26×6.5
=183.69(立方厘米)
答:圆柱的体积是183.69立方厘米,表面积是178.98平方厘米。
图二:3.14×72×9
=3.14×49×9
=153.86×9
=1384.74
=461.58(立方厘米)
答:圆锥的体积是461.58立方厘米。
图三:(16×10+16×6.5+10×6.5)×2
=(160+104+65)×2
=329×2
=658(平方厘米)
16×10×6.5
=160×6.5
=1040(立方厘米)
答:长方体的表面积是658平方厘米,体积是 1040立方厘米。
【点评】此题考查圆柱表面积和体积、圆锥体积、长方表面积和体积的计算。掌握它们的计算公式是解答的关键。
35.(7分)(2023春 仓山区期中)我们有6位大人和12位小孩子要到动物园里游玩,至少要花多少钱购票?
动物园门票
成人每人 20元
儿童每人 10元
团体10人及以上每人 15元
【考点】最优化问题.
【专题】优化问题;创新意识.
【答案】230元。
【分析】先用人数乘票价分别求出成人和小孩花的钱,再相加求出单买的总价;再用总人数乘团体票价求出购买团体票的总价;然后让6个大人和4个小孩买团体票,剩下的孩子买儿童票,求出总价;最后比较三种购买方法的钱数,确定答案。
【解答】解:20×6+10×12
=120+120
=240(元)
(6+12)×15
=18×15
=270(元)
(6+4)×15+(12﹣4)×10
=150+80
=230(元)
230<240<270
答:至少要花230元钱购票。
【点评】本题考查的是最优化问题,关键是确定购买方案,分别算出总价再比较,选取花钱最少的方案。
第1页(共1页)
一.填空题(共13小题,满分27分)
1.(2分)(2023春 澄迈县月考)在第一次检测中,六(1)班数学科的平均分是88分。如果以平均分为标准,张强和李远的成绩分别是﹣2和6,则他们的实际成绩分别是 分和 分。
2.(4分)(2023 徐闻县)0.25= ÷ =9: = %
3.(2分)如果5m=7n(m≠0,n≠0),那么m和n成 比例;如果(y≠0),那么x和y成 比例。
4.(1分)(2022 岷县模拟)已知比例的两个内项的积是,一个外项是两个内项积的倒数,另一个外项是 。
5.(2分)(2021 龙港区)三角形的面积一定,底和高成 比例;工作时间一定,工作总量和工作效率成 比例。
6.(3分)(2023 奈曼旗)国家出台了建设新农村的政策,我的家乡也已经开始进行街道规划了,街道规划平面图上标的比例尺是它表示 。把它写成数值比例尺的形式是 。在这幅地图上从政府大楼到我家的距离是7cm,那么我家到政府大楼的实际距离是 。
A、图上的1cm的距离相当于实际的100km
B、图上的1cm的距离相当于实际的50km
C、1:5000000
D、1:10000000
E、350km
F、700km
7.(2分)(2023春 松江区期中)60平方分米= 平方米
4.25立方米= 立方分米
8.(3分)(2022秋 郏县期末)
0.25立方米= 升 升= 毫升 40分= 时
9.(3分)如图,把底面半径3cm,高10cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的底面积是 cm2,表面积是 cm2,体积是 cm3。
10.(1分)(2021秋 迎江区期末)被减数、减数与差三个数的和是72,差与减数的比4:5,差是 ,减数是 。
11.(1分)把一个圆柱的侧面展开后得到一个正方形,若圆柱的底面直径是4cm,则圆柱的高是 cm。
12.(1分)(2021春 邱县期中)用36个完全一样的圆锥形铁坯,可以铸成 个与圆锥等底等高的圆柱。
13.(2分)(2023春 灵山县期中)将一个圆柱沿直径切开,得到两个边长是16厘米的正方形切面。原来圆柱的表面积是 平方厘米,体积是 立方厘米。
二.选择题(共6小题,满分6分,每小题1分)
14.(1分)(2024 襄城县)如图,b对应的数最有可能是( )
A.0 B.﹣3 C.+2 D.﹣1
15.(1分)(2021 河东区)比例的两个外项分别是2和5,下面列出的比例正确的是( )
A.2:5=1:2.5 B.2.5:2=5:4 C.2:2.5=4:5 D.5:4=3:2
16.(1分)张师傅加工一个零件需要小时,李师傅加工相同的一个零件需要小时,张师傅与李师傅的工作效率之比为( )
A.2:3 B.3:2 C.2:5
17.(1分)(2020秋 定兴县期末)根据3M=5N(M,N均不为0)可以写成不同的比例,下面比例式正确的是( )
A.M:N=3:5 B.M:3=5:N C.5:3=M:N D.M:3=N:5
18.(1分)(2022春 新晃县期中)一个圆柱和一个圆锥等底等高,它们的体积之和是52dm3,那么这个圆柱的体积是( )dm3。
A.13 B.26 C.39
19.(1分)(2022春 电白区期中)如图,把一个底面周长是18.84厘米、高是5厘米的圆柱体横截成二段,表面积增加( )平方厘米。
A.141.3 B.56.52 C.94.2
三.判断题(共6小题,满分6分,每小题1分)
20.(1分)(2023 永寿县)长方形的长一定,长方形的面积和宽成正比例。
21.(1分)(2022 即墨区)圆的周长和它的半径成反比例关系。
22.(1分)(2024 茌平区)比例的一个外项扩大到原来的2倍,一个内项缩小到原来的,比例仍然成立。
23.(1分)(2021春 蓝田县期中)一个圆柱的侧面积是376.8dm2,底面半径是2dm,这它的高是60dm。
24.(1分)(2023 赞皇县)当圆柱、正方体、长方体的底面周长相等,高也相等时,圆柱的体积最大。
25.(1分)(2022 杭州模拟)用20个小正方体搭一个长方体,不管怎样搭,体积都相等。
四.计算题(共2小题,满分16分)
26.(6分)
3.53+47= 125×16= 7.2÷0.05÷20= 3.9×30%= 9.6÷0.6=
3.3×4.9+5.1×3.3= 0.72÷3.6= 0.77+0.33= (15.4﹣0.4)×4= 0.7﹣0.08=
0.27×0.7= 0.53×5+0.47×5= 300÷2.5= 0.25+7.85= 6.4+2.5×4=
45= 7.2÷0.4=
54.8%﹣39.9%= 24=
(
83%﹣38%= 0.36÷36%= 3.85﹣1.36﹣1.64= 2.68÷0.04= 5.61﹣1.1=
27.(10分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
五.操作题(共3小题,满分14分)
28.(4分)(2023秋 天河区期末)请你在方格纸上画一个长4厘米、宽2厘米的长方形,再算一算,要画一个与这个长方形周长相等的正方形,它的边长是 厘米。
29.(4分)(2024 邳州市模拟)如图是某地区的平面示意图。
(1)中原桃花岛位于汇龙国际 偏 °方向 米处。
(2)文景苑位于汇龙国际正西100米处,请在图中标出它的位置。
(3)文苑路位于解放路北侧100米,并与解放路平行,在图中用线表示出来。
30.(6分)(2024秋 惠济区期末)市政府准备在圆形喷水池附近修建一个周长是30米的长方形花坛,使它的长与宽的比是2:1,请你在如图画出长方形花坛的示意图。(每个小方格的边长表示1米)
六.解答题(共5小题,满分31分)
31.(6分)小明想知道学校旗杆的高度,他的方法是,选择一根竹竿,把1.8米长的竹竿直立在旗杆旁,量得它的影长是1.5米,同时量得学校旗杆的影长是6米,现在你能算出旗杆的高度吗?(用比例解)
32.(6分)如图,一个用塑料薄膜覆盖的蔬菜大棚长40 m,横截面是一个直径为6m的半圆。
①这个蔬菜大棚的占地面积是多少平方米?
②搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(只有一端用塑料薄膜封闭)
(6分)(2024 尧都区模拟)有一种饮料瓶,瓶身呈圆柱形(不包括瓶颈),瓶子的容积是480mL,现在瓶中装有一些饮料,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,求瓶内现有多少毫升饮料?
34.(6分)(2023 邢台模拟)求下列图形的体积和表面积。(圆锥不用求表面积)单位:厘米。
图一:表面积:体积:
图二:体积:
图三:表面积:体积:
35.(7分)(2023春 仓山区期中)我们有6位大人和12位小孩子要到动物园里游玩,至少要花多少钱购票?
动物园门票
成人每人 20元
儿童每人 10元
团体10人及以上每人 15元
上海市2024-2025学年六年级下学期期中综合测试数学试卷
参考答案与试题解析
一.填空题(共13小题,满分27分)
1.(2分)(2023春 澄迈县月考)在第一次检测中,六(1)班数学科的平均分是88分。如果以平均分为标准,张强和李远的成绩分别是﹣2和6,则他们的实际成绩分别是 86 分和 94 分。
【考点】负数的意义及其应用.
【专题】综合填空题;数感.
【答案】86,94。
【分析】以平均分为标准,﹣2表示比平均分少2分,6表示比平均分多6分,据此计算他们的实际成绩。
【解答】解:以平均分88分为标准,张强的成绩是﹣2,就是比88分少2分,他的实际成绩是86分,李远的成绩是6,就是比88分多6分,他的实际成绩是94分。
故答案为:86,94。
【点评】此题主要考查正负数的意义。
2.(4分)(2023 徐闻县)0.25= 1 ÷ 4 =9: 36 = 25 %
【考点】比与分数、除法的关系;小数、分数和百分数之间的关系及其转化.
【专题】综合填空题;数据分析观念.
【答案】1;4;36;25。
【分析】小数化成除法算式,0.25=1÷4;由分除法算式转化成比,根据比的基本性质,比的前项和后项同时乘或除以相同的数,(0除外)比值不变,最后由小数转化成百分数,将小数乘100,得到25,然后在后面加上百分号,即25%。
【解答】解:0.25=1÷4=(1×9):(4×9)=9:36
0.25=25%
则0.25=1÷4=9÷36=25%。
故答案为:1;4;36;25。
【点评】此题考查了小数、除法算式和百分数之间的互化,要求学生掌握。
3.(2分)如果5m=7n(m≠0,n≠0),那么m和n成 正 比例;如果(y≠0),那么x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例.
【答案】正,反。
【分析】两个相关联的量,如果它们的乘积一定,则这两个量成反比例,如果它们的比值一定,则这两个量成正比例;先根据两个关系式推出m和n、x和y相乘或相除等于一个不变的量,从而再进行判断。
【解答】解:如果5m=7n(m≠0,n≠0),变式为,那么m和n成正比例;
如果(y≠0),变式为xy=30,那么x和y成反比例。
故答案为:正,反。
【点评】本题考查的是正、反比例的认识,关键是掌握什么叫正、反比例。
4.(1分)(2022 岷县模拟)已知比例的两个内项的积是,一个外项是两个内项积的倒数,另一个外项是 。
【考点】比例的意义和基本性质.
【专题】常规题型;能力层次.
【答案】。
【分析】依据比例的基本性质,即两内项之积等于两外项之积,已知比例内项之积是,那么两外项的积也是,其中一个外项是内项之积的倒数,即其中一个外项是(1),(1)即可求出另一个外项。
【解答】解:1
答:另一个外项是。
故答案为:。
【点评】解答此题的主要依据是:比例的基本性质以及倒数的求法。
5.(2分)(2021 龙港区)三角形的面积一定,底和高成 反 比例;工作时间一定,工作总量和工作效率成 正 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】反,正。
【分析】底×高=三角形的面积×2,工作总量÷工作效率=工作时间。据此解答。
【解答】解:三角形的面积一定,底和高成反比例;工作时间一定,工作总量和工作效率成正比例。
故答案为:反,正。
【点评】两个相关联的量,若它们的比值一定,这两个量成正比例关系;若它们的乘积一定,这两个量成反比例关系。
6.(3分)(2023 奈曼旗)国家出台了建设新农村的政策,我的家乡也已经开始进行街道规划了,街道规划平面图上标的比例尺是它表示 B 。把它写成数值比例尺的形式是 C 。在这幅地图上从政府大楼到我家的距离是7cm,那么我家到政府大楼的实际距离是 E 。
A、图上的1cm的距离相当于实际的100km
B、图上的1cm的距离相当于实际的50km
C、1:5000000
D、1:10000000
E、350km
F、700km
【考点】比例尺;图上距离与实际距离的换算(比例尺的应用).
【专题】比和比例;应用意识.
【答案】B、C、E。
【分析】根据线段比例尺的意义,可知这个街道规划平面图上标的比例尺中图上1厘米相当于实际50千米;再根据比例尺=图上距离:实际距离,把线段比例尺改写成数值比例尺;最后根据图上1厘米相当于实际50千米,则图上7厘米就相当于实际7个50千米,用乘法求出我家到政府大楼的实际距离。
【解答】解:(1)街道规划平面图上标的比例尺表示图上1厘米相当于实际50千米;
(2)写成数值比例尺是:1厘米:50千米
=1厘米:5000000厘米
=1:5000000
(3)50×7=350(千米)
故答案为:B、C、E。
【点评】本题考查比例尺的意义以及应用。关键是区分线段比例尺、数值比例尺的意义,并能熟练应用。
7.(2分)(2023春 松江区期中)60平方分米= 0.6 平方米
4.25立方米= 4250 立方分米
【考点】小面积单位间的进率及单位换算;体积、容积进率及单位换算.
【专题】常见的量.
【答案】0.6;4250。
【分析】根据1平方米=100平方分米,1立方米=1000立方分米,解答此题即可。
【解答】解:60平方分米=0.6平方米
4.25立方米=4250立方分米
故答案为:0.6;4250。
【点评】熟练掌握面积单位、体积单位的换算,是解答此题的关键。
8.(3分)(2022秋 郏县期末)
0.25立方米= 250 升 升= 600 毫升 40分= 时
【考点】体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算.
【专题】长度、面积、体积单位;质量、时间、人民币单位;数据分析观念.
【答案】250,600,。
【分析】1立方米=1000立方分米=1000升,1立方分米=1升=1000立方厘米,1时=60秒分,利用单位之间的换算的方法:大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率,据此解答。
【解答】解:
0.25立方米=250升 升=600毫升 40分时
故答案为:250,600,。
【点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。
9.(3分)如图,把底面半径3cm,高10cm的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的底面积是 28.26 cm2,表面积是 304.92 cm2,体积是 282.6 cm3。
【考点】圆柱的侧面积、表面积和体积.
【专题】综合填空题;几何直观.
【答案】28.26、304.92、282.6。
【分析】依据题意结合图示可知,长方体的底面积等于圆柱的底面积,表面积等于圆柱的表面积加上2个长是10厘米,宽是3厘米的长方形的面积,体积等于圆柱的体积,由此解答本题。
【解答】解:3.14×3×3
=3.14×9
=28.26(cm2)
28.26×2+3.14×3×2×10+2×10×3
=56.52+188.4+60
=304.92(cm2)
3.14×3×3×10
=3.14×90
=282.6(cm3)
答:这个长方体的底面积是28.26cm2,表面积是304.92cm2,体积是282.6cm3。
故答案为:28.26、304.92、282.6。
【点评】本题考查的是圆柱的表面积、体积公式的应用。
10.(1分)(2021秋 迎江区期末)被减数、减数与差三个数的和是72,差与减数的比4:5,差是 16 ,减数是 20 。
【考点】按比例分配应用题.
【专题】运算能力.
【答案】16,20。
【分析】因为被减数=减数+差,因此被减数、减数、差三个数的和等于减数与差之和的2倍,因此减数与差之和是72÷2=36,然后根据减数与差的比,用按比例分配的方法解决问题。
【解答】解:72÷2=36
3616
3620
答:差是16,减数是20。
故答案为:16,20。
【点评】此题解答的关键在于根据被减数、减数、差之间的关系,求出减数与差二者之和,进而解决问题。
11.(1分)把一个圆柱的侧面展开后得到一个正方形,若圆柱的底面直径是4cm,则圆柱的高是 12.56 cm。
【考点】圆柱的展开图.
【专题】平面图形的认识与计算;空间观念.
【答案】12.56。
【分析】因为圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于圆柱的高,由此根据圆的周长公式C=πd,求出圆柱的底面周长,即圆柱的高。
【解答】解:3.14×4=12.56(厘米)
答:圆柱的高是12.56厘米。
故答案为:12.56。
【点评】此题主要考查了圆柱的侧面展开图与圆柱的关系,如果圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于圆柱的高。
12.(1分)(2021春 邱县期中)用36个完全一样的圆锥形铁坯,可以铸成 12 个与圆锥等底等高的圆柱。
【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】12。
【分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以3个圆锥形钢材可以熔铸成一个与它等底等高的圆柱。
【解答】解:36÷3=12(个)
答:可以铸成12个与圆锥等底等高的圆柱。
故答案为:12。
【点评】解答此题的依据是圆锥体积是与它等底等高的圆柱体积的。
13.(2分)(2023春 灵山县期中)将一个圆柱沿直径切开,得到两个边长是16厘米的正方形切面。原来圆柱的表面积是 1205.76 平方厘米,体积是 3215.36 立方厘米。
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】1205.76,3215.36。
【分析】根据题意可知,把这个圆柱沿着底面直径并垂直于底面切开,若切面是边长16厘米的正方形,由此可知,这个圆柱的底面直径和高都是16厘米,圆柱的表面积公式:S表=S侧+S底×2,圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×16×16+3.14×(16÷2)2×2
=3.14×256+3.14×64×2
=3.14×384
=1205.76(平方厘米)
3.14×(16÷2)2×16
=3.14×64×16
=200.96×16
=3215.36(立方厘米)
答:原来圆柱的表面积是1205.76平方厘米,体积是3215.36立方厘米。
故答案为:1205.76,3215.36。
【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是熟记公式。
二.选择题(共6小题,满分6分,每小题1分)
14.(1分)(2024 襄城县)如图,b对应的数最有可能是( )
A.0 B.﹣3 C.+2 D.﹣1
【考点】数轴的认识.
【专题】数感.
【答案】D
【分析】根据数轴的认识,将﹣2到3之间平均分成5段,b占其中的一点,靠近﹣2,所以为﹣1,据此解答即可。
【解答】解:如图:
b对应的数最有可能是﹣1。
故选:D。
【点评】本题考查数轴的认识。
15.(1分)(2021 河东区)比例的两个外项分别是2和5,下面列出的比例正确的是( )
A.2:5=1:2.5 B.2.5:2=5:4 C.2:2.5=4:5 D.5:4=3:2
【考点】比例的意义和基本性质.
【专题】推理能力.
【答案】C
【分析】组成比例的四个数叫做比例的项,中间的两个数叫做比例的内项,两端的两个数叫做比例的外项。据此选择即可。
【解答】解:AB中比例的两个外项不是2和5,不符合题意。
C.比例的两个外项不是2和5,并且2×5=2.5×4=10,符合题意。
D.5:4=1.25,3:2=1.5,1.25≠1.5,式子本身不成立,不符合题意。
故选:C。
【点评】此题主要是考查了比例的意义,学生需熟练掌握。
16.(1分)张师傅加工一个零件需要小时,李师傅加工相同的一个零件需要小时,张师傅与李师傅的工作效率之比为( )
A.2:3 B.3:2 C.2:5
【考点】比的意义;简单的工程问题.
【专题】运算能力.
【答案】A
【分析】由于完成相同的工作量,所用时间与工作效率成反比,则张师傅和李师傅工作效率的比是:。
【解答】解::2:3
答:张师傅与李师傅的工作效率的比为2:3。
故选:A。
【点评】本题是一道有关比的认识、简单的工程问题的题目,完成相同的工作量,用的时间越短,效率越高。
17.(1分)(2020秋 定兴县期末)根据3M=5N(M,N均不为0)可以写成不同的比例,下面比例式正确的是( )
A.M:N=3:5 B.M:3=5:N C.5:3=M:N D.M:3=N:5
【考点】比例的意义和基本性质.
【专题】比和比例;推理能力.
【答案】C
【分析】比例的性质:在比例中,两个外项的积等于两个内项的积,这叫做比例的基本性质,据此把等式3M=5N看作两外项或两内项的积,转换成比例式即可。
【解答】解:因为3M=5N,所以M:N=5:3,也就是5:3=M:N。
故选:C。
【点评】此题主要考查比例的基本性质:在比例里,两内项的积等于两外项的积。
18.(1分)(2022春 新晃县期中)一个圆柱和一个圆锥等底等高,它们的体积之和是52dm3,那么这个圆柱的体积是( )dm3。
A.13 B.26 C.39
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【专题】立体图形的认识与计算;空间观念.
【答案】C
【分析】因为等底等高的圆锥的体积是圆柱体积的,所以等底等高的圆柱与圆锥的体积和相当于圆柱体积的(1),然后用除法解答即可。
【解答】解:52÷(1)
=39(立方分米)
答:圆柱的体积是39立方分米。
故选:C。
【点评】此题主要考查等底等高的圆柱与圆锥体积之间关系的灵活运用。
19.(1分)(2022春 电白区期中)如图,把一个底面周长是18.84厘米、高是5厘米的圆柱体横截成二段,表面积增加( )平方厘米。
A.141.3 B.56.52 C.94.2
【考点】圆柱的侧面积、表面积和体积.
【专题】几何直观.
【答案】B
【分析】如果把它切割成2段,表面积增加的是2个圆柱的底面积,由此利用面积公式S=πr2进行解答。先求出一个底面的面积,再乘2,即可求出表面积增加多少平方厘米。
【解答】解:18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
28.26×2=56.52(平方厘米)
答:表面积增加56.52平方厘米。
故选:B。
【点评】本题考查圆柱底面积的计算,熟练掌握公式是解决本题的关键。
三.判断题(共6小题,满分6分,每小题1分)
20.(1分)(2023 永寿县)长方形的长一定,长方形的面积和宽成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;运算能力.
【答案】√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答即可。
【解答】解:因为长方形的面积÷宽=长方形的长(一定),是商一定,所以长方形的长一定,长方形的面积与宽成正比例;所以原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21.(1分)(2022 即墨区)圆的周长和它的半径成反比例关系。 ×
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:圆的周长÷半径=2π(一定),是比值一定,所以圆的周长和它的半径成正比例关系,所以本题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22.(1分)(2024 茌平区)比例的一个外项扩大到原来的2倍,一个内项缩小到原来的,比例仍然成立。 ×
【考点】比例的意义和基本性质.
【专题】比和比例;推理能力.
【答案】×
【分析】在比例里,一个外项扩大原来的2倍,要使比例照样成立,另一个外项要缩小到原来的;也可以使其中一个内项扩大原来的2倍;此题也可采用举例验证的方法解决。
【解答】解:根据分析可知,比例的一个外项扩大到原来的2倍,一个外项缩小到原来的,比例仍然成立。原题说法错误。
故答案为:×。
【点评】此题考查比例基本性质的运用:在比例里,两个内项的积等于两个外项的积。
23.(1分)(2021春 蓝田县期中)一个圆柱的侧面积是376.8dm2,底面半径是2dm,这它的高是60dm。 ×
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】要求这个圆柱体的高是多少分米,先要计算出圆柱的底面周长,根据圆柱的底面周长计算公式“C=2πr”,代入数值,计算出底面周长;然后根据“圆柱的高=侧面积÷底面周长”代入数字,进行解答即可。
【解答】解:376.8÷(2×3.14×2)
=376.8÷12.56
=30(dm)
答:它的高是30dm。
故答案为:×。
【点评】本题主要考查圆柱体侧面积计算公式的应用,此类题解答时应明确圆柱的底面周长和底面半径的关系,然后根据圆柱的侧面积、底面周长和高之间的关系进行分析解答即可得出结论。
24.(1分)(2023 赞皇县)当圆柱、正方体、长方体的底面周长相等,高也相等时,圆柱的体积最大。 √
【考点】圆柱的侧面积、表面积和体积.
【专题】立体图形的认识与计算;几何直观.
【答案】√
【分析】根据圆的周长公式:C=2πr,正方形的周长公式:C=4a,长方形的周长公式:C=(a+b)×2,因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大,再根据圆柱、正方体、长方体的统一体积公式:V=Sh,所以圆柱、正方体和长方体的底面周长相等,高也相等时,圆柱的体积最大。据此解答即可。
【解答】解:因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大,再根据圆柱、正方体、长方体的统一体积公式:V=Sh,所以圆柱、正方体和长方体的底面周长相等,高也相等时,圆柱的体积最大。原题说法正确。
故答案为:√。
【点评】解答此题的关键是明确:因为在平面图形中,当圆的周长、正方形的周长、长方形的周长相等时,圆的面积最大。
25.(1分)(2022 杭州模拟)用20个小正方体搭一个长方体,不管怎样搭,体积都相等。 √
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】√
【分析】由于长方体都是由20个小正方体搭成的,所以体积不变,由此求解。
【解答】解:无论怎么搭,搭成的长方体都是20个小正方体的体积和,所以体积不变。故题干说法正确。
故答案为:√。
【点评】本题考查了对体积的认识,明确小正方体的个数不变,搭成的体积不变。
四.计算题(共2小题,满分16分)
26.(6分)
3.53+47= 125×16= 7.2÷0.05÷20= 3.9×30%= 9.6÷0.6=
3.3×4.9+5.1×3.3= 0.72÷3.6= 0.77+0.33= (15.4﹣0.4)×4= 0.7﹣0.08=
0.27×0.7= 0.53×5+0.47×5= 300÷2.5= 0.25+7.85= 6.4+2.5×4=
45= 7.2÷0.4=
54.8%﹣39.9%= 24=
(
83%﹣38%= 0.36÷36%= 3.85﹣1.36﹣1.64= 2.68÷0.04= 5.61﹣1.1=
【考点】分数的四则混合运算;小数的加法和减法;小数乘法;小数除法.
【专题】运算能力.
【答案】50.53,2000,7.2,1.17,16,33,0.2,1.1,60,0.62,0.189,5,120,8.1,16.4,,35,,,18,2,,0.149,,,,,,,2,0.45,1,0.85,67,4.51,5。
【分析】根据整数、分数、小数、百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
3.53+47=50.53 125×16=2000 7.2÷0.05÷20=7.2 3.9×30%=1.17 9.6÷0.6=16
3.3×4.9+5.1×3.3=33 0.72÷3.6=0.2 0.77+0.33=1.1 (15.4﹣0.4)×4=60 0.7﹣0.08=0.62
0.27×0.7=0.189 0.53×5+0.47×5=5 300÷2.5=120 0.25+7.85=8.1 6.4+2.5×4=16.4
45=35 7.2÷0.4=18
2 54.8%﹣39.9%=0.149 24
(2
83%﹣38%=0.45 0.36÷36%=1 3.85﹣1.36﹣1.64=0.85 2.68÷0.04=67 5.61﹣1.1=4.51
5
【点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
27.(10分)(2023 海淀区模拟)解方程。
1xx﹣2
4x:(3﹣x):0.75
【考点】分数方程求解;解比例.
【专题】简易方程;运算能力.
【答案】x=11,x,x=7。
【分析】(1)根据等式的性质可得x,接下来对方程两边同时除以,求出x的值,即可解答;
(2)根据比例的性质可得(3﹣x)=4x×0.75,接下来根据等式的性质进行求解,即可解答;
(3)根据比例的性质可得6×(x﹣2)=5×(x﹣1),接下来根据等式的性质进行求解,即可解答。
【解答】解:1xx﹣2
x
x=11
4x:(3﹣x):0.75
(3﹣x)=4x×0.75
1x=3x
x=1
1
x
6(x﹣2)=5(x﹣1)
6x﹣12=5x﹣5
6x﹣5x=12﹣5
x=7
【点评】本题是一道关于解方程与解比例的题目,解答本题的关键是掌握等式的性质与比例的性质。
五.操作题(共3小题,满分14分)
28.(4分)(2023秋 天河区期末)请你在方格纸上画一个长4厘米、宽2厘米的长方形,再算一算,要画一个与这个长方形周长相等的正方形,它的边长是 3 厘米。
【考点】画指定长、宽(边长)的长方形、正方形.
【专题】平面图形的认识与计算;几何直观.
【答案】
【分析】根据题意,长方形的周长=(长+宽)×2,正方形的周长=边长×4,那么先画一个长厘米4厘米,宽2厘米的长方形,周长为12厘米的正方形的边长可为3厘米。
【解答】解:正方形的边长:
(4+2)×2÷4
=6×2÷4
=12÷4
=3(厘米)
作图如下:
【点评】此题主要考查的是如何根据周长确定正方形的边长,然后再作图即可。
29.(4分)(2024 邳州市模拟)如图是某地区的平面示意图。
(1)中原桃花岛位于汇龙国际 东 偏 南60 °方向 200 米处。
(2)文景苑位于汇龙国际正西100米处,请在图中标出它的位置。
(3)文苑路位于解放路北侧100米,并与解放路平行,在图中用线表示出来。
【考点】在平面图上标出物体的位置;根据方向和距离确定物体的位置.
【专题】图形与位置;应用意识.
【答案】(1)东,南60,200;(2)、(3)。
【分析】(1)根据上北下南左西右东的方向以及距离和角度,即可解答;
(2)根据上北下南左西右东的方向以及距离,即可解答;
(3)根据上北下南左西右东的方向以及距离作解放路平行线,即可解答。
【解答】解:(1)10000×2=20000(厘米)
20000厘米=200米
答:中原桃花岛位于汇龙国际东偏南60°方向200米处。
(2)、(3)100米=10000厘米
10000÷10000=1(厘米)
(2)、(3)作图如下:
故答案为:东,南60,200。
【点评】本题考查的是在平面上标出物体的位置,掌握上北下南左西右东的方向是解答关键。
30.(6分)(2024秋 惠济区期末)市政府准备在圆形喷水池附近修建一个周长是30米的长方形花坛,使它的长与宽的比是2:1,请你在如图画出长方形花坛的示意图。(每个小方格的边长表示1米)
【考点】比的应用;长方形的周长.
【专题】几何直观;应用意识.
【答案】
【分析】长方形周长÷2=长宽和,将比的前后项看成份数,长宽和÷总份数=一份数,一份数分别乘长和宽的对应份数,求出长和宽,作图即可。
【解答】解:30÷2=15(米)
15÷(2+1)
=15÷3
=5(米)
5×2=10(米)
5×1=5(米)
画出的长方形花坛长10米,宽5米,作图如下:
【点评】本题主要考查比的应用以及周长的周长公式。
六.解答题(共5小题,满分31分)
31.(6分)小明想知道学校旗杆的高度,他的方法是,选择一根竹竿,把1.8米长的竹竿直立在旗杆旁,量得它的影长是1.5米,同时量得学校旗杆的影长是6米,现在你能算出旗杆的高度吗?(用比例解)
【考点】正、反比例应用题.
【专题】比和比例应用题;应用意识.
【答案】7.2米。
【分析】由题可知,同一时刻物体的长度与影长成正比例据此列出比例解答即可。
【解答】解:设学校的旗杆高为x米。
1.8:1.5=x:6
1.5x=1.8×6
1.5x=10.8
x=7.2
答:学校的旗杆高7.2米。
【点评】本题是一道有关正、反比例的应用的题目,掌握正比例的判断方法是解题的关键。
32.(6分)如图,一个用塑料薄膜覆盖的蔬菜大棚长40 m,横截面是一个直径为6m的半圆。
①这个蔬菜大棚的占地面积是多少平方米?
②搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(只有一端用塑料薄膜封闭)
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】①240平方米:②390.93平方米。
【分析】①蔬菜大棚的占地面积即长为40m、宽为6m的长方形的面积。
②至少需要塑料薄膜的面积=直径为6m的圆面积的一半+圆柱侧面积的一半。
【解答】解:①6×40=240(m2)
答:这个蔬菜大棚的占地面积是240平方米。
②3.14×(6÷2)2÷2+3.14×6÷2×40
=14.13+9.42×40
=14.13+376.8
=390.93(m2)
答:搭建这个蔬菜大棚至少要用390.93平方米的塑料薄膜。
【点评】本题考查的是圆柱的应用题,熟记圆柱的底面积、侧面积、表面积公式是解答关键。
33.(6分)(2024 尧都区模拟)有一种饮料瓶,瓶身呈圆柱形(不包括瓶颈),瓶子的容积是480mL,现在瓶中装有一些饮料,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,求瓶内现有多少毫升饮料?
【考点】关于圆柱的应用题.
【专题】立体图形的认识与计算.
【答案】400毫升。
【分析】根据题意,瓶子的容积是480mL,瓶子正放时饮料高度为20cm,倒放时空余部分的高度为4cm,瓶子的容积相当于高是(20+4)的圆柱的容积,所以底面积是480÷(20+4)=20(平方厘米),所以瓶内现有饮料体积=20×20=400(毫升),据此解答。
【解答】解:480÷(20+4)
=480÷24
=20(cm2)
20×20=400(mL)
答:瓶内现有400毫升饮料。
【点评】本题考查了圆柱的体积的相关知识,解决本题的关键是求出圆柱的底面积。
34.(6分)(2023 邢台模拟)求下列图形的体积和表面积。(圆锥不用求表面积)单位:厘米。
图一:表面积:体积:
图二:体积:
图三:表面积:体积:
【考点】圆柱的侧面积、表面积和体积;圆锥的体积;长方体和正方体的表面积;长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】图一:178.98平方厘米;183.69立方厘米;图二:461.58立方厘米;图三:658平方厘米;1040立方厘米。
【分析】图一:首先求出圆柱的底面半径,圆柱的体积=πr2h,圆柱表面积=2πr2+2πrh,代入数据计算即可解答。
图二:圆锥体积πr2h,代入数据计算即可解答。
图三:长方体体积=长×宽×高,长方体表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可解答。
【解答】解:图一:6÷2=3(厘米)
3.14×6×6.5
=18.84×6.5
=122.46(平方厘米)
3.14×32×2
=3.14×9×2
=28.26×2
=56.52(平方厘米)
122.46+56.52=178.98(平方厘米)
3.14×32×6.5
=3.14×9×6.5
=28.26×6.5
=183.69(立方厘米)
答:圆柱的体积是183.69立方厘米,表面积是178.98平方厘米。
图二:3.14×72×9
=3.14×49×9
=153.86×9
=1384.74
=461.58(立方厘米)
答:圆锥的体积是461.58立方厘米。
图三:(16×10+16×6.5+10×6.5)×2
=(160+104+65)×2
=329×2
=658(平方厘米)
16×10×6.5
=160×6.5
=1040(立方厘米)
答:长方体的表面积是658平方厘米,体积是 1040立方厘米。
【点评】此题考查圆柱表面积和体积、圆锥体积、长方表面积和体积的计算。掌握它们的计算公式是解答的关键。
35.(7分)(2023春 仓山区期中)我们有6位大人和12位小孩子要到动物园里游玩,至少要花多少钱购票?
动物园门票
成人每人 20元
儿童每人 10元
团体10人及以上每人 15元
【考点】最优化问题.
【专题】优化问题;创新意识.
【答案】230元。
【分析】先用人数乘票价分别求出成人和小孩花的钱,再相加求出单买的总价;再用总人数乘团体票价求出购买团体票的总价;然后让6个大人和4个小孩买团体票,剩下的孩子买儿童票,求出总价;最后比较三种购买方法的钱数,确定答案。
【解答】解:20×6+10×12
=120+120
=240(元)
(6+12)×15
=18×15
=270(元)
(6+4)×15+(12﹣4)×10
=150+80
=230(元)
230<240<270
答:至少要花230元钱购票。
【点评】本题考查的是最优化问题,关键是确定购买方案,分别算出总价再比较,选取花钱最少的方案。
第1页(共1页)
同课章节目录
