9.1 平移 自主学习解答题专题训练 (含答案)苏科版七年级数学下册
文档属性
| 名称 | 9.1 平移 自主学习解答题专题训练 (含答案)苏科版七年级数学下册 | 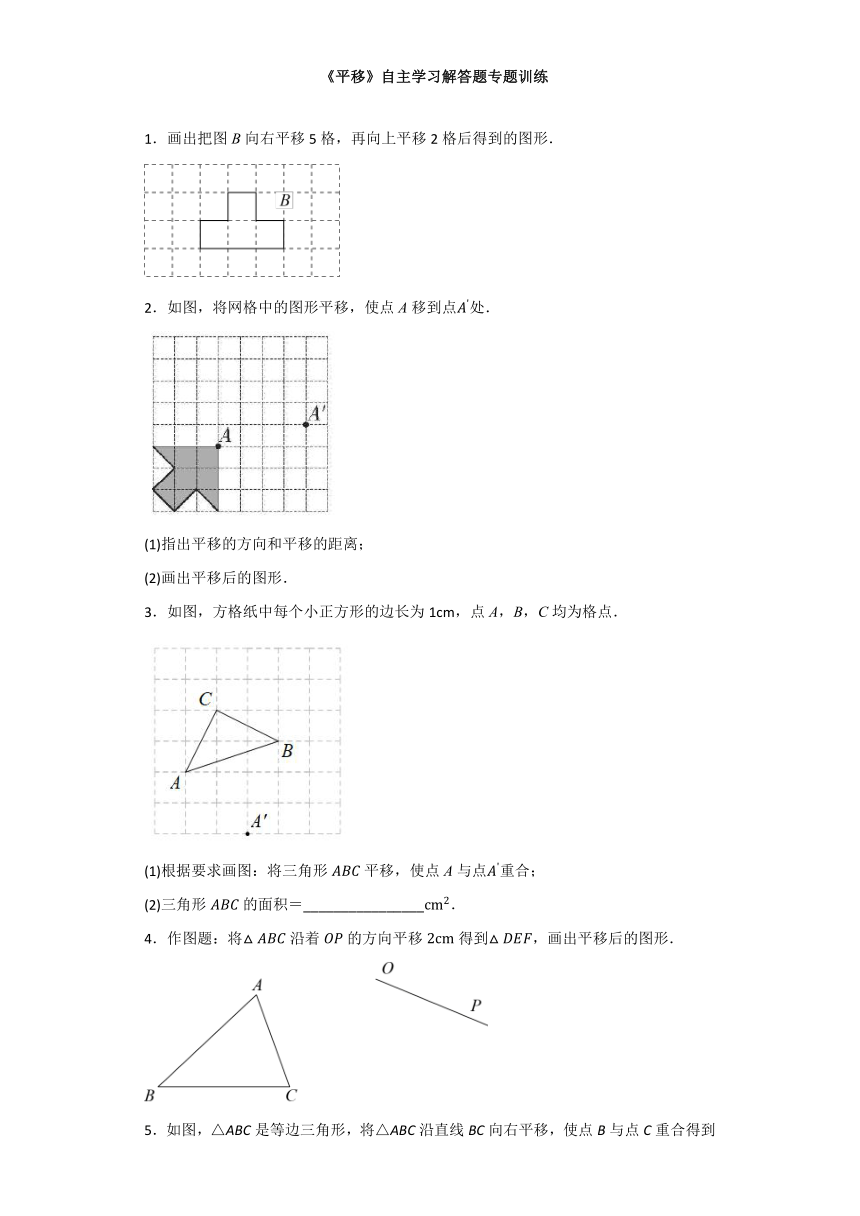 | |
| 格式 | docx | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 08:01:03 | ||
图片预览





文档简介
《平移》自主学习解答题专题训练
1.画出把图B向右平移5格,再向上平移2格后得到的图形.
2.如图,将网格中的图形平移,使点A移到点处.
(1)指出平移的方向和平移的距离;
(2)画出平移后的图形.
3.如图,方格纸中每个小正方形的边长为1cm,点A,B,C均为格点.
(1)根据要求画图:将三角形平移,使点A与点重合;
(2)三角形的面积=________________.
4.作图题:将沿着的方向平移得到,画出平移后的图形.
5.如图,△ABC是等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合得到△DCE,连接BD交AC于点F.猜想AC与BD的位置关系,并证明你的结论.
6.如图,沿直线向右平移,得到,,.
(1)求的长;
(2)求的度数.
7.如图,三角形沿方向平移到三角形的位置.
(1)当时,求的度数;
(2)当,时,求平移的距离.
8.某酒店在重新装修后,准备在门口的阶梯上铺设某种红色地毯.已知这种地毯每平方米的售价为元,阶梯道宽为米,其侧面如图所示,铺设阶梯的红地毯至少需要多长?至少花费多少元?
9.如图,两个直角三角形重叠在一起,将三角形沿点到点的方向平移到三角形的位置,已知,,平移的距离为6.求图中阴影部分的面积.
10.如图,将向右平移,使点移动到点,点移动到点,点移动到点,且,.
(1)画出平移后的;
(2)若,求的长度(用含有的式子表示).
11.如图,的边长为.将平移得到,且,求阴影部分的面积.
12.如图,在中,,,,沿方向平移至,若,.求:
(1)沿方向平移的距离;
(2)四边形的周长.
13.如图两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
14.如图,将沿射线的方向平移个单位到的位置,点的对应点分别点.
(1)若,则______.
(2)若,求的度数.
15.如图,线段AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,.将线段AE沿着直线AC平移得到线段PQ,连接DQ.
(1)求证:;
(2)若,,求的度数.
16.如图,已知直线,,点、在边上,且满足,平分.
(1)求的度数;
(2)若平行移动,那么:的值是否随之发生变化?若变化,请找出变化的规律;若不变,求出这个比值.
17.如图,都是由平移得到的图形,A、C、F三点在同一条直线上.已知.
(1)求的长;
(2)求的度数.
18.如图,在四边形中,与互余,将分别平移到和的位置.
(1)请判断的形状,并说明理由;
(2)若,求的长.
19.如图1,长方形的边在数轴上,为原点,长方形的面积为24,边长为4.
(1)数轴上点表示的数为________.
(2)将长方形沿数轴水平移动,移动后的长方形记为,移动后的长方形与原长方形重叠部分的面积记为.
①当恰好等于原长方形面积的一半时,数轴上点表示的数为________.
②设点的移动距离.
当时,________;
为线段的中点,点在线段上,且,当点,所表示的数互为相反数时,求的值.
20.如图1,已知线段、线段被直线所截于点、点,,的度数是的倍少.
(1)求证:;
(2)如图2,连接,沿方向平移得到,点在上,点是上的一点,连接,,,求的度数;
(3)如图3,点是线段上一点,点是射线上一点,度数为,度数为,度数为,请直接写出、、之间的数量关系.(本题的角均小于)
参考答案
1.解:如图所示:
2.解:(1)如图,连接,平移的方向是点A到点的方向,平移的距离是线段的长度.
(2)如图,该图形即为所求.
3.(1)解:将先水平向右移动两个单位长度,再竖直向下移动两个单位长度,即可得到点A于点重合,即如图所示:
(2)解:由题意可得:,
故答案为.
4.解:如图,即为所求.
5.解:AC⊥BD.证明如下:
∵△ABC是等边三角形,
,.
∵△DCE是由△ABC平移得到的,
,,
.
又,
,
,.
6.解:(1)由平移知,.
∵,
∴;
(2)由平移知,
,
.
7.(1)解:由平移可知,
.
(2)由平移可知,
,
,
,
平移的距离为.
8.解:依题意,地毯的长度至少为(米),
(元).
答:铺设阶梯的红地毯至少需要米,花费至少元.
9.解:将沿点到点的方向平移到的位置,
,,,
∴,
∴,
.
10.(1)解:如图所示,
即为所求;
(2)解:∵平移,,
∴,
∴
11.解:∵将平移得到,
∴,
∵,
∴四边形是长方形,,
∴阴影部分的面积长方形的面积.
12.解:(1)∵沿方向平移至,
∴.
∵,
∴ ;
即沿方向平移的距离是.
(2)由平移的性质可得:,
∵,
∴四边形的周长 .
∴四边形的周长是.
13.(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
14.(1)解:∵将沿射线的方向平移个单位到的位置,
∴,
∵,
∴,
故答案为;
(2)解:由平移的性质可知:,,
∴,,
∵,
∴,
∴.
15.解:(1)证明:,.
,,.
(2)如图,过点D作DF∥AE交AB于点F,则.
∵,
由平移的性质,得,
,.
,,
,
,
16.(1)解:∵,,
,
,平分,
,,
,
∴,即,
;
(2)解:不变化
因为平行移动,
∵,
,
∵,
,
:的值恒等于:.
17.(1)解:∵都是由平移得到,
∴,
∴.
(2)解:∵ ,
∴,
∵都是由平移得到,
∴.
18.解:(1)是直角三角形.
理由:分别平移到和的位置,
,
.
与互余,
,
.
,
,
是直角三角形.
(2)分别平移到和的位置,
.
.
,
.
19.(1)解:∵长方形的面积为24.边长为4.
∴,
∴,
∵为原点,
∴点A表示的数为6,
故答案为:6.
(2)解:①∵S等于原长方形面积的一半,
∴,
当向左运动时,如图,
,即,
解得,
∴点表示的数为3;
当向右运动时,如图,
,即,
解得,
∴,
∴,
∴点表示的数为9;
故答案为:3或9;
②∵,
∴,
∴,
故答案为:;
∵点D、E所表示的数互为相反数
∴长方形只能向左平移,如图
∵为线段的中点,点在线段上,,
∴点D表示的数为,点E表示的数为:,
∴,
解得.
20.(1)证明:,的度数是的倍少,
,
,
,
;
(2)过作,
,
,
,
,
;
(3) ,
与()同理可得:,
,
,
,,
,
.
即.
1.画出把图B向右平移5格,再向上平移2格后得到的图形.
2.如图,将网格中的图形平移,使点A移到点处.
(1)指出平移的方向和平移的距离;
(2)画出平移后的图形.
3.如图,方格纸中每个小正方形的边长为1cm,点A,B,C均为格点.
(1)根据要求画图:将三角形平移,使点A与点重合;
(2)三角形的面积=________________.
4.作图题:将沿着的方向平移得到,画出平移后的图形.
5.如图,△ABC是等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合得到△DCE,连接BD交AC于点F.猜想AC与BD的位置关系,并证明你的结论.
6.如图,沿直线向右平移,得到,,.
(1)求的长;
(2)求的度数.
7.如图,三角形沿方向平移到三角形的位置.
(1)当时,求的度数;
(2)当,时,求平移的距离.
8.某酒店在重新装修后,准备在门口的阶梯上铺设某种红色地毯.已知这种地毯每平方米的售价为元,阶梯道宽为米,其侧面如图所示,铺设阶梯的红地毯至少需要多长?至少花费多少元?
9.如图,两个直角三角形重叠在一起,将三角形沿点到点的方向平移到三角形的位置,已知,,平移的距离为6.求图中阴影部分的面积.
10.如图,将向右平移,使点移动到点,点移动到点,点移动到点,且,.
(1)画出平移后的;
(2)若,求的长度(用含有的式子表示).
11.如图,的边长为.将平移得到,且,求阴影部分的面积.
12.如图,在中,,,,沿方向平移至,若,.求:
(1)沿方向平移的距离;
(2)四边形的周长.
13.如图两个有重叠的直角三角形,可以看作是将其中的一个直角三角形沿着方向平移5个单位长度就得到了另一直角三角形,其中.
(1)填空:线段与线段的关系为________.
(2)求四边形的面积;
(3)连接,若,,求的度数.
14.如图,将沿射线的方向平移个单位到的位置,点的对应点分别点.
(1)若,则______.
(2)若,求的度数.
15.如图,线段AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥AB,连接AE,.将线段AE沿着直线AC平移得到线段PQ,连接DQ.
(1)求证:;
(2)若,,求的度数.
16.如图,已知直线,,点、在边上,且满足,平分.
(1)求的度数;
(2)若平行移动,那么:的值是否随之发生变化?若变化,请找出变化的规律;若不变,求出这个比值.
17.如图,都是由平移得到的图形,A、C、F三点在同一条直线上.已知.
(1)求的长;
(2)求的度数.
18.如图,在四边形中,与互余,将分别平移到和的位置.
(1)请判断的形状,并说明理由;
(2)若,求的长.
19.如图1,长方形的边在数轴上,为原点,长方形的面积为24,边长为4.
(1)数轴上点表示的数为________.
(2)将长方形沿数轴水平移动,移动后的长方形记为,移动后的长方形与原长方形重叠部分的面积记为.
①当恰好等于原长方形面积的一半时,数轴上点表示的数为________.
②设点的移动距离.
当时,________;
为线段的中点,点在线段上,且,当点,所表示的数互为相反数时,求的值.
20.如图1,已知线段、线段被直线所截于点、点,,的度数是的倍少.
(1)求证:;
(2)如图2,连接,沿方向平移得到,点在上,点是上的一点,连接,,,求的度数;
(3)如图3,点是线段上一点,点是射线上一点,度数为,度数为,度数为,请直接写出、、之间的数量关系.(本题的角均小于)
参考答案
1.解:如图所示:
2.解:(1)如图,连接,平移的方向是点A到点的方向,平移的距离是线段的长度.
(2)如图,该图形即为所求.
3.(1)解:将先水平向右移动两个单位长度,再竖直向下移动两个单位长度,即可得到点A于点重合,即如图所示:
(2)解:由题意可得:,
故答案为.
4.解:如图,即为所求.
5.解:AC⊥BD.证明如下:
∵△ABC是等边三角形,
,.
∵△DCE是由△ABC平移得到的,
,,
.
又,
,
,.
6.解:(1)由平移知,.
∵,
∴;
(2)由平移知,
,
.
7.(1)解:由平移可知,
.
(2)由平移可知,
,
,
,
平移的距离为.
8.解:依题意,地毯的长度至少为(米),
(元).
答:铺设阶梯的红地毯至少需要米,花费至少元.
9.解:将沿点到点的方向平移到的位置,
,,,
∴,
∴,
.
10.(1)解:如图所示,
即为所求;
(2)解:∵平移,,
∴,
∴
11.解:∵将平移得到,
∴,
∵,
∴四边形是长方形,,
∴阴影部分的面积长方形的面积.
12.解:(1)∵沿方向平移至,
∴.
∵,
∴ ;
即沿方向平移的距离是.
(2)由平移的性质可得:,
∵,
∴四边形的周长 .
∴四边形的周长是.
13.(1)解:由题意得:线段与线段的关系为平行且相等,
故答案为:平行且相等;
(2)解:由平移知,,
∴,
∵三角形的面积=三角形的面积,
∴四边形的面积=四边形的面积
;
(3)解:由平移知,,,
∴,,
∵,
∴.
14.(1)解:∵将沿射线的方向平移个单位到的位置,
∴,
∵,
∴,
故答案为;
(2)解:由平移的性质可知:,,
∴,,
∵,
∴,
∴.
15.解:(1)证明:,.
,,.
(2)如图,过点D作DF∥AE交AB于点F,则.
∵,
由平移的性质,得,
,.
,,
,
,
16.(1)解:∵,,
,
,平分,
,,
,
∴,即,
;
(2)解:不变化
因为平行移动,
∵,
,
∵,
,
:的值恒等于:.
17.(1)解:∵都是由平移得到,
∴,
∴.
(2)解:∵ ,
∴,
∵都是由平移得到,
∴.
18.解:(1)是直角三角形.
理由:分别平移到和的位置,
,
.
与互余,
,
.
,
,
是直角三角形.
(2)分别平移到和的位置,
.
.
,
.
19.(1)解:∵长方形的面积为24.边长为4.
∴,
∴,
∵为原点,
∴点A表示的数为6,
故答案为:6.
(2)解:①∵S等于原长方形面积的一半,
∴,
当向左运动时,如图,
,即,
解得,
∴点表示的数为3;
当向右运动时,如图,
,即,
解得,
∴,
∴,
∴点表示的数为9;
故答案为:3或9;
②∵,
∴,
∴,
故答案为:;
∵点D、E所表示的数互为相反数
∴长方形只能向左平移,如图
∵为线段的中点,点在线段上,,
∴点D表示的数为,点E表示的数为:,
∴,
解得.
20.(1)证明:,的度数是的倍少,
,
,
,
;
(2)过作,
,
,
,
,
;
(3) ,
与()同理可得:,
,
,
,,
,
.
即.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
