苏科版八年级数学上册2.4《线段、角的轴对称性》教学课件(共25张PPT)
文档属性
| 名称 | 苏科版八年级数学上册2.4《线段、角的轴对称性》教学课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 852.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-03 21:17:28 | ||
图片预览



文档简介
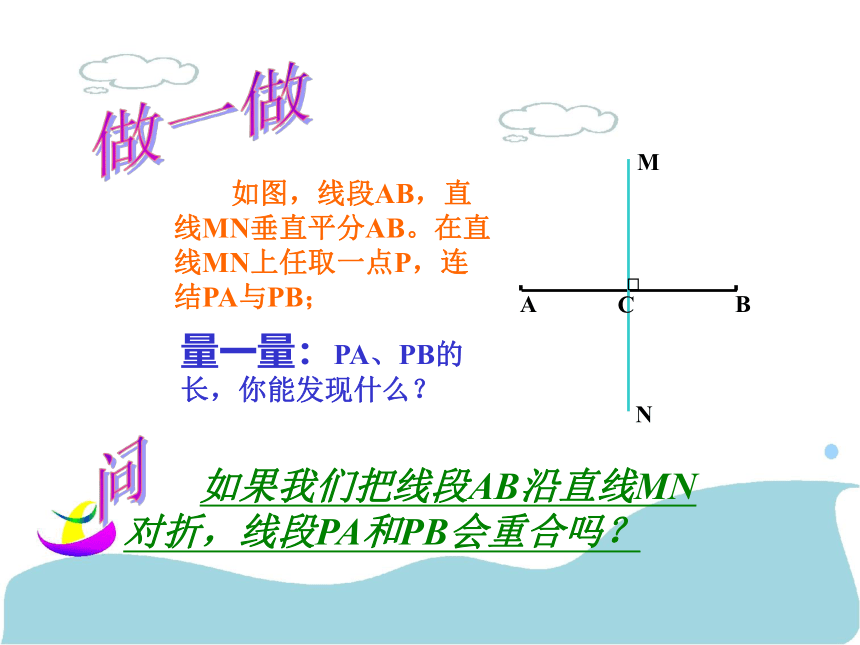
课件25张PPT。线段、角的轴对称性(1)宜兴外国语学校:初二备课组沪 宁 高 速 公 路 在沪宁高速公路l的同侧,有两个化工厂A、B,为了便于两厂的货物运输,市政府计划在公路边上修建一处高速入口,使得两个工厂的工人都没意见,问入口应选在何处?AB阿Q的难题 如图,线段AB,直线MN垂直平分AB。在直线MN上任取一点P,连结PA与PB; 如果我们把线段AB沿直线MN对折,线段PA和PB会重合吗?问量一量:PA、PB的长,你能发现什么?
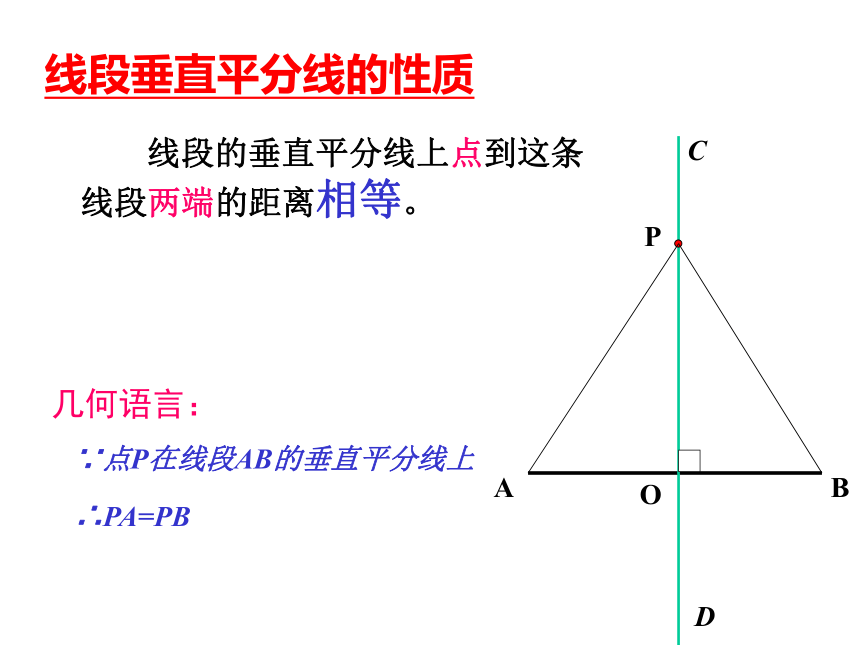
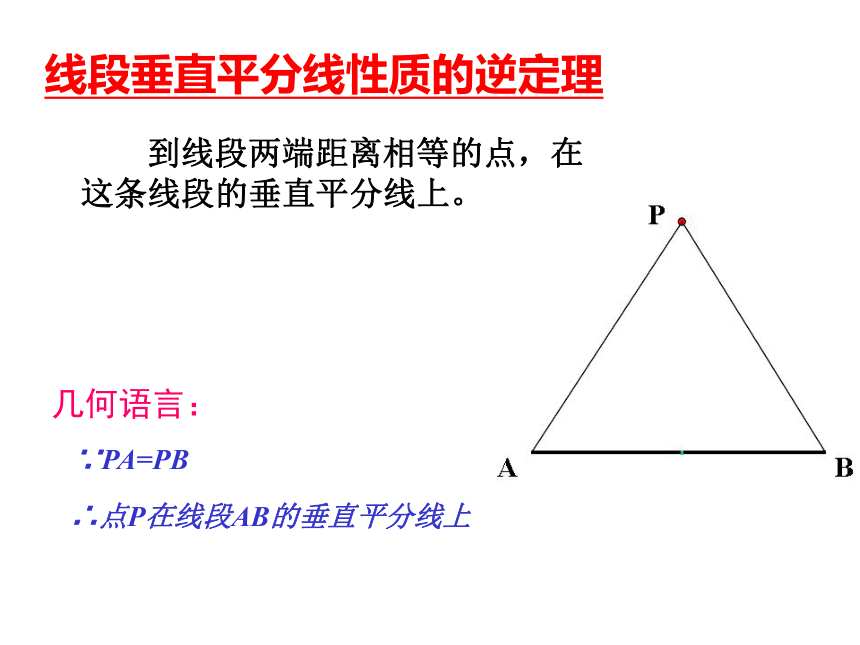
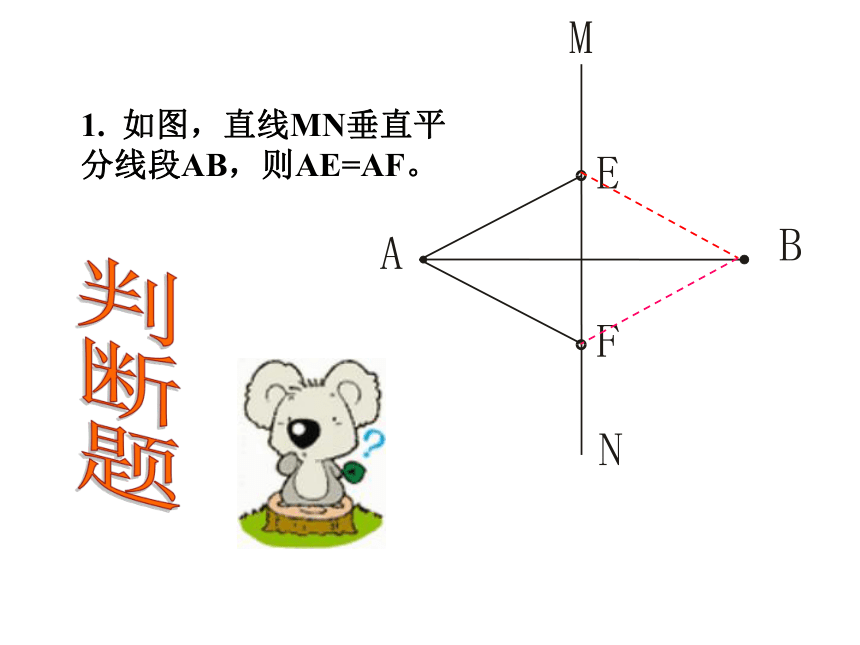
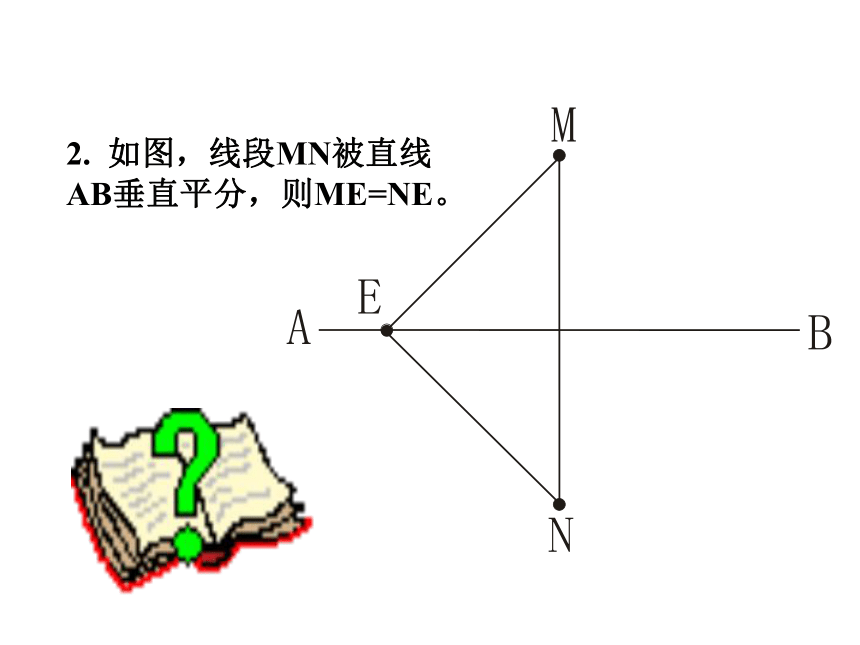
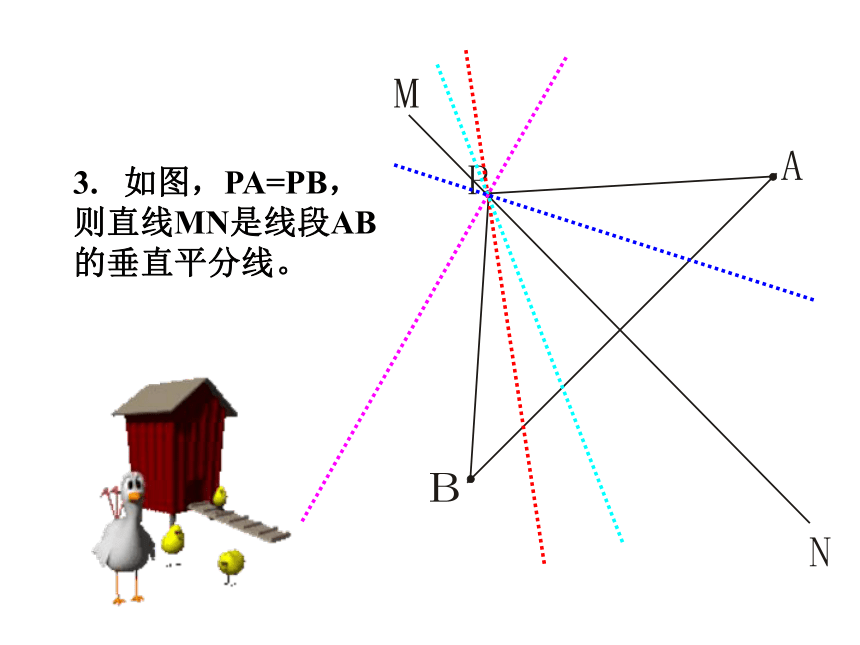
做一做O∴PA=PB∵点P在线段AB的垂直平分线上 线段的垂直平分线上点到这条线段两端的距离相等。线段垂直平分线的性质几何语言:线段的垂直平分线外的点,到这条线段两端的距离相等吗?为什么? 如图,在线段AB的垂直平分线l外任取一点P,连接PA、PB,PA交l于点Q,PA与PB相等吗?为什么? 想一想符号语言∴点P在线段AB的垂直平分线上∵PA=PB 到线段两端距离相等的点,在这条线段的垂直平分线上。线段垂直平分线性质的逆定理几何语言:1. 如图,直线MN垂直平分线段AB,则AE=AF。判断题2. 如图,线段MN被直线AB垂直平分,则ME=NE。3. 如图,PA=PB,则直线MN是线段AB的垂直平分线。填空题1. 到线段两端距离相等的点有________个。无 数2. 一条线段的垂直平分线有______ 条。1 你会用直尺和圆规画已知线段的垂直平分线吗?作一作思考:为什么你所作直线就是线段
AB的垂直平分线? 沪 宁 高 速 公 路 在沪宁高速公路l的同侧,有两个化工厂A、B,为了便于两厂的货物运输,市政府计划在公路边上修建一处高速入口P,使得两个工厂的工人都没意见,问入口P应选在何处?AB阿Q的难题 例1、如图,在直线l上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务。P 例1、如图,在直线l上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务。 变形:把点A、B改为在直线l的两侧。 现有三个村庄甲、乙、丙,现要新建一个水泵站P,使它到三个村庄的距离相等,应建在何处?(画出点P的位置)例2 已知:如图,在ΔABC中, 边AB、BC的垂直平分线交于P.
求证:PA=PB=PC例2 已知:如图,在ΔABC中,边AB、BC的垂直平分线交于P.求证:PA=PB=PC.证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
∴PA=PB=PC.例3已知:如图,在等腰三角形ABC中,腰AB的垂直平分线MN交腰AC于D,BC=8厘米,ΔBDC的周长为20厘米。求:AB的长.解: ∵MN是线段AB的垂直平行线,
∴ AD = BD (线段垂直平分线上的点和这条线段两个端点的距离相等)
∴ ΔBDC的周长 = BD + DC + BC
= AD + DC + BC 20cm
= AC+ BC
=20cm
∵ BC = 8cm
∴ AC = 12 cm
∵ AB和AC是等腰三角形△ABC的腰
∴ AB = AC= 12cm 3.如图, ABC中,已知AC=27,
AB的垂直平分线DE交AB,AC于E,D, BCD
周长为50,求BC的长.AEBDCAEBCD例4如图,D是BC延长线上的一点,BD=BC+AC,
求证:点C在AD的垂直平分线上 例5在△ABC中,ON是AB的垂直平分线,OA=OC
求证:点O在BC 的垂直平分线上想一想:你能得到什么结论?结论: 三角形三边的垂直平分线交于一点,这一点
到三角形三个顶点的距离相等。小结再见! 通过预习你已经掌握
了哪些知识?※
做一做O∴PA=PB∵点P在线段AB的垂直平分线上 线段的垂直平分线上点到这条线段两端的距离相等。线段垂直平分线的性质几何语言:线段的垂直平分线外的点,到这条线段两端的距离相等吗?为什么? 如图,在线段AB的垂直平分线l外任取一点P,连接PA、PB,PA交l于点Q,PA与PB相等吗?为什么? 想一想符号语言∴点P在线段AB的垂直平分线上∵PA=PB 到线段两端距离相等的点,在这条线段的垂直平分线上。线段垂直平分线性质的逆定理几何语言:1. 如图,直线MN垂直平分线段AB,则AE=AF。判断题2. 如图,线段MN被直线AB垂直平分,则ME=NE。3. 如图,PA=PB,则直线MN是线段AB的垂直平分线。填空题1. 到线段两端距离相等的点有________个。无 数2. 一条线段的垂直平分线有______ 条。1 你会用直尺和圆规画已知线段的垂直平分线吗?作一作思考:为什么你所作直线就是线段
AB的垂直平分线? 沪 宁 高 速 公 路 在沪宁高速公路l的同侧,有两个化工厂A、B,为了便于两厂的货物运输,市政府计划在公路边上修建一处高速入口P,使得两个工厂的工人都没意见,问入口P应选在何处?AB阿Q的难题 例1、如图,在直线l上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务。P 例1、如图,在直线l上求作一点P,使PA=PB.数学问题源于生活实践,反过来数学又为生活实践服务。 变形:把点A、B改为在直线l的两侧。 现有三个村庄甲、乙、丙,现要新建一个水泵站P,使它到三个村庄的距离相等,应建在何处?(画出点P的位置)例2 已知:如图,在ΔABC中, 边AB、BC的垂直平分线交于P.
求证:PA=PB=PC例2 已知:如图,在ΔABC中,边AB、BC的垂直平分线交于P.求证:PA=PB=PC.证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
∴PA=PB=PC.例3已知:如图,在等腰三角形ABC中,腰AB的垂直平分线MN交腰AC于D,BC=8厘米,ΔBDC的周长为20厘米。求:AB的长.解: ∵MN是线段AB的垂直平行线,
∴ AD = BD (线段垂直平分线上的点和这条线段两个端点的距离相等)
∴ ΔBDC的周长 = BD + DC + BC
= AD + DC + BC 20cm
= AC+ BC
=20cm
∵ BC = 8cm
∴ AC = 12 cm
∵ AB和AC是等腰三角形△ABC的腰
∴ AB = AC= 12cm 3.如图, ABC中,已知AC=27,
AB的垂直平分线DE交AB,AC于E,D, BCD
周长为50,求BC的长.AEBDCAEBCD例4如图,D是BC延长线上的一点,BD=BC+AC,
求证:点C在AD的垂直平分线上 例5在△ABC中,ON是AB的垂直平分线,OA=OC
求证:点O在BC 的垂直平分线上想一想:你能得到什么结论?结论: 三角形三边的垂直平分线交于一点,这一点
到三角形三个顶点的距离相等。小结再见! 通过预习你已经掌握
了哪些知识?※
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
