2025年中考数学二轮复习课件: 专题一 基础夯实·反比例函数 课件(25张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习课件: 专题一 基础夯实·反比例函数 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 14:19:21 | ||
图片预览








文档简介
(共25张PPT)
2025年数学中考复习
专题一 基础夯实
反比例函数
知识点1 反比例函数的定义
一般地,形如_ _____是常数, 的函数叫作反比例函数,其他
表示形式有__________或_______。
知识点2 反比例函数的图像及其质
解析式
图像 _______________________________________ _______________________________________
所在象限 第①________象限 第②________象限
增减性
一、三
二、四
减小
增大
取值范围
图像特点
对称 性 中心对称图形:图像关于⑧__________中心对称
轴对称图形:图像关于直线⑨______对称,也关于直线⑩
________对称
无限接近
坐标原点
续表
知识点3 确定反比例函数的解析式
1.利用待定系数法确定反比例函数解析式
(1)设所求反比例函数解析式为 ;
(2)找出图像上一点,代入 ;
(3)确定反比例函数解析式 。
2.利用定义确定反比例函数解析式
利用定义求反比例函数解析式时,令自变量的指数等于 ,并且注
意反比例函数解析式中。例:若函数 是反比例函数,
则且 。
3.利用面积确定反比例函数解析式
已知面积时可考虑反比例函数中的几何意义,由面积得 ,再结合图
像所在象限判断的符号,从而得到 的值,代入解析式即可。
知识点4 反比例函数 的几何意义
在的图像上任意一点,过这一点分别作轴、 轴
的垂线,,两垂线与坐标轴围成的矩形的面积为 。
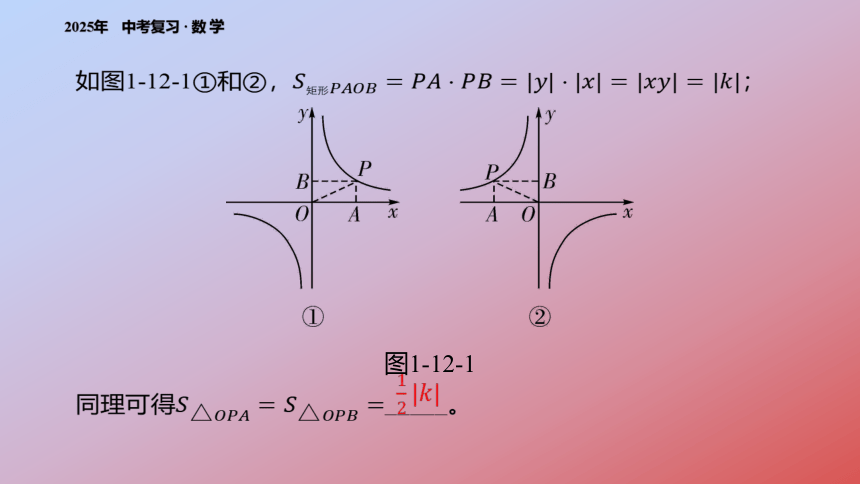
如图1-12-1①和②, ;
图1-12-1
同理可得 _____。
知识点5 反比例函数的综合应用
1.反比例函数的实际应用
(1)根据实际情况建立反比例函数模型;
(2)利用待定系数法或跨学科公式确定函数解析式;
(3)根据反比例函数的性质解决实际问题。
温馨提示 实际问题中的反比例函数,一般自变量的取值范围会因实
际情况受到限制,这时反比例函数图像可能是双曲线的一支或一段,因此
要注意自变量和函数的取值范围。
2.反比例函数与一次函数的综合
(1)确定交点坐标:联立两个函数解析式求解;
(2)确定函数解析式:先确定交点坐标,再利用待定系数法求解。
三角形与特殊三角形
知识点1 三角形的分类、边角关系
1. 三角形的分类
2.三角形三边关系
文字语言 理论 依据 应用
三角形两 边的和 ①______ 第三边 ③___ _____ _____ _____ _____ (1)判断三条线段能否组成
三角形;注:判断三条线段能
否构成三角形,应将两条短
线段的和与最长线段作比
较;
(2)已知三角形的两边,求
第三边的取值范围
三角形两 边的差 ②______ 第三边 大于
两点之间,线段最短
小于
3.三角形角的关系
(1)三角形内角和定理:三角形的三个内角和等于______。
(2)推论:①直角三角形两个锐角______,两个锐角______的三角形
是直角三角形;②三角形外角性质:三角形的任何一个外角等于与其
_________的两个内角的和;③三角形的一个外角______任何一个和它不
相邻的内角。
温馨提示 同一个三角形中,等角对等边;等边对等角;大角对大边;
大边对大角;等角的补角相等;等角的余角相等。
4.三角形的稳定性:三角形具有稳定性,而四边形不具有稳定性。三
角形的稳定性具有广泛的应用,例如:桥梁、起重机、“人”字形屋顶等。
互余
互余
不相邻
大于
知识点2 三角形中的重要线段
名称 图示 性质 拓展
高线 ①______:三角形三条高线
所在直线的交点
垂心
名称 图示 性质 拓展
中线 重心:三角形三条中线的交
点;重心到三角形顶点的
距离等于它到顶点对边中
点距离的2倍
续表
名称 图示 性质 拓展
角平分 线 内心:三角形三条角平分
线的交点;内心到三角形三
边距离相等,内心即三角
形内切圆的圆心
续表
名称 图示 性质 拓展
中位线 ____________________________________________________
求作三角形中位线时,既可以
找到一边中点(作垂直平分线找中
点),再作平行(如图①);也可
以找到两边中点连接(如图②)
续表
知识点3 等腰三角形的性质与判定
等 腰 三 角 形 性 质 (1)等腰三角形的两腰①______;
(2)等腰三角形两底角②______;
(3)等腰三角形的顶角的角平分线、③______________、
④______________互相重合(简称“三线合一”);
(4)等腰三角形是轴对称图形,有⑤______对称轴
判 定 (1)(定义法)有两条边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形(简称“等角对等
边”)
相等
相等
底边上的高线
底边上的中线
一条
知识点4 等边三角形的性质与判定
等边 三角 形 性质 (1)等边三角形的三边①______;
(2)等边三角形的三个内角②______,都等于③____;
(3)等边三角形是轴对称图形,且有④___条对称轴;
(4)等边三角形任意一边上的高线、中线及其对角的角平
分线互相重合(简称“三线合一”)
相等
相等
3
等边 三角 形 判定 (1)三条边都⑤______的三角形是等边三角形;
(2)三个内角都⑥______的三角形是等边三角形;
(3)有一个角是⑦____的等腰三角形是等边三角形
面 积
相等
相等
续表
知识点5 直角三角形的性质与判定
直角 三角 形 性质
斜边的一半
斜边
平方和
直角 三角 形 判定
面 积
互余
续表
感谢您的观看
2025年数学中考复习
专题一 基础夯实
反比例函数
知识点1 反比例函数的定义
一般地,形如_ _____是常数, 的函数叫作反比例函数,其他
表示形式有__________或_______。
知识点2 反比例函数的图像及其质
解析式
图像 _______________________________________ _______________________________________
所在象限 第①________象限 第②________象限
增减性
一、三
二、四
减小
增大
取值范围
图像特点
对称 性 中心对称图形:图像关于⑧__________中心对称
轴对称图形:图像关于直线⑨______对称,也关于直线⑩
________对称
无限接近
坐标原点
续表
知识点3 确定反比例函数的解析式
1.利用待定系数法确定反比例函数解析式
(1)设所求反比例函数解析式为 ;
(2)找出图像上一点,代入 ;
(3)确定反比例函数解析式 。
2.利用定义确定反比例函数解析式
利用定义求反比例函数解析式时,令自变量的指数等于 ,并且注
意反比例函数解析式中。例:若函数 是反比例函数,
则且 。
3.利用面积确定反比例函数解析式
已知面积时可考虑反比例函数中的几何意义,由面积得 ,再结合图
像所在象限判断的符号,从而得到 的值,代入解析式即可。
知识点4 反比例函数 的几何意义
在的图像上任意一点,过这一点分别作轴、 轴
的垂线,,两垂线与坐标轴围成的矩形的面积为 。
如图1-12-1①和②, ;
图1-12-1
同理可得 _____。
知识点5 反比例函数的综合应用
1.反比例函数的实际应用
(1)根据实际情况建立反比例函数模型;
(2)利用待定系数法或跨学科公式确定函数解析式;
(3)根据反比例函数的性质解决实际问题。
温馨提示 实际问题中的反比例函数,一般自变量的取值范围会因实
际情况受到限制,这时反比例函数图像可能是双曲线的一支或一段,因此
要注意自变量和函数的取值范围。
2.反比例函数与一次函数的综合
(1)确定交点坐标:联立两个函数解析式求解;
(2)确定函数解析式:先确定交点坐标,再利用待定系数法求解。
三角形与特殊三角形
知识点1 三角形的分类、边角关系
1. 三角形的分类
2.三角形三边关系
文字语言 理论 依据 应用
三角形两 边的和 ①______ 第三边 ③___ _____ _____ _____ _____ (1)判断三条线段能否组成
三角形;注:判断三条线段能
否构成三角形,应将两条短
线段的和与最长线段作比
较;
(2)已知三角形的两边,求
第三边的取值范围
三角形两 边的差 ②______ 第三边 大于
两点之间,线段最短
小于
3.三角形角的关系
(1)三角形内角和定理:三角形的三个内角和等于______。
(2)推论:①直角三角形两个锐角______,两个锐角______的三角形
是直角三角形;②三角形外角性质:三角形的任何一个外角等于与其
_________的两个内角的和;③三角形的一个外角______任何一个和它不
相邻的内角。
温馨提示 同一个三角形中,等角对等边;等边对等角;大角对大边;
大边对大角;等角的补角相等;等角的余角相等。
4.三角形的稳定性:三角形具有稳定性,而四边形不具有稳定性。三
角形的稳定性具有广泛的应用,例如:桥梁、起重机、“人”字形屋顶等。
互余
互余
不相邻
大于
知识点2 三角形中的重要线段
名称 图示 性质 拓展
高线 ①______:三角形三条高线
所在直线的交点
垂心
名称 图示 性质 拓展
中线 重心:三角形三条中线的交
点;重心到三角形顶点的
距离等于它到顶点对边中
点距离的2倍
续表
名称 图示 性质 拓展
角平分 线 内心:三角形三条角平分
线的交点;内心到三角形三
边距离相等,内心即三角
形内切圆的圆心
续表
名称 图示 性质 拓展
中位线 ____________________________________________________
求作三角形中位线时,既可以
找到一边中点(作垂直平分线找中
点),再作平行(如图①);也可
以找到两边中点连接(如图②)
续表
知识点3 等腰三角形的性质与判定
等 腰 三 角 形 性 质 (1)等腰三角形的两腰①______;
(2)等腰三角形两底角②______;
(3)等腰三角形的顶角的角平分线、③______________、
④______________互相重合(简称“三线合一”);
(4)等腰三角形是轴对称图形,有⑤______对称轴
判 定 (1)(定义法)有两条边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形(简称“等角对等
边”)
相等
相等
底边上的高线
底边上的中线
一条
知识点4 等边三角形的性质与判定
等边 三角 形 性质 (1)等边三角形的三边①______;
(2)等边三角形的三个内角②______,都等于③____;
(3)等边三角形是轴对称图形,且有④___条对称轴;
(4)等边三角形任意一边上的高线、中线及其对角的角平
分线互相重合(简称“三线合一”)
相等
相等
3
等边 三角 形 判定 (1)三条边都⑤______的三角形是等边三角形;
(2)三个内角都⑥______的三角形是等边三角形;
(3)有一个角是⑦____的等腰三角形是等边三角形
面 积
相等
相等
续表
知识点5 直角三角形的性质与判定
直角 三角 形 性质
斜边的一半
斜边
平方和
直角 三角 形 判定
面 积
互余
续表
感谢您的观看
同课章节目录
