九年级数学下册试题 第三章《 圆》全章知识点复习题--北师大版(含解析)
文档属性
| 名称 | 九年级数学下册试题 第三章《 圆》全章知识点复习题--北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 21:52:32 | ||
图片预览




文档简介
第三章《 圆》全章知识点复习题
【题型1 垂径定理的应用】
1.如图,一座石桥的主桥拱是四弧形,某时刻添得水面的宽度为8米,拱高(的中点C到水面的距离)为2米.
(1)求主桥拱所在圆的半径.
(2)在主桥拱所在圆的圆心处有一水位检测仪,若过几天某时刻的水面为,检测仪观测点的仰角为,求此时水面的宽度.(参考数据:,,)
2.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.如图,用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).这根圆柱形木材的直径是多少寸?
3.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一类似问题“今有圆材埋在壁中,不知大小.以锯锯之,深两寸,锯道长一尺二,问径几何 ”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为寸,锯道尺(尺寸),求该圆材的直径为多少寸
4.如图,装有水的水槽放在水平桌面上,其横截面是以为直径的半圆O,,为桌面截线,水面截线,直径一端点B刚好与点N重合,.
(1)计算的长度,并比较直径与长度的大小;
(2)请在图中画出线段,用其长度表示水的最大深度,并求水的最大深度.
【题型2 弧、弦、圆心角的关系】
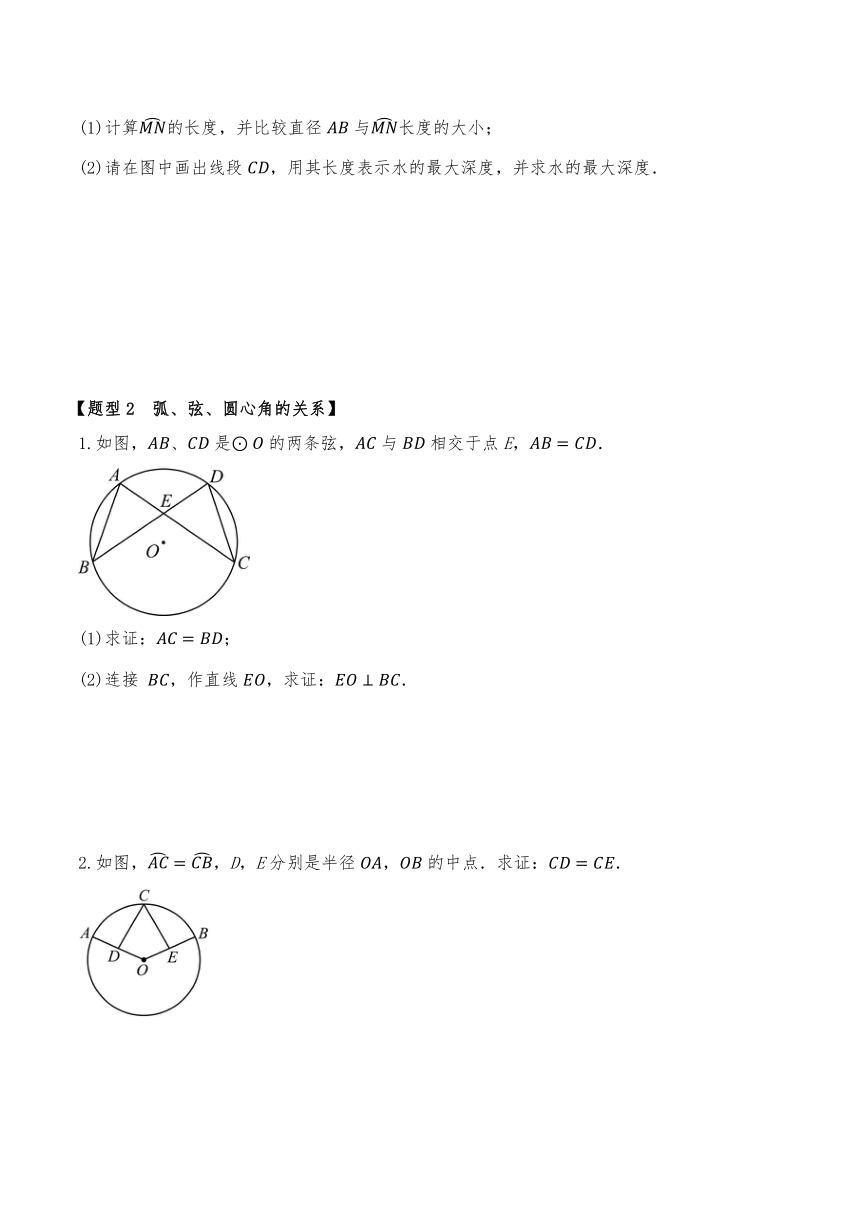
1.如图,、是的两条弦,与相交于点E,.
(1)求证:;
(2)连接 作直线求证:.
2.如图,,D,E分别是半径,的中点.求证:.
3.已知,如图,在中,,,求证:.
4.已知是圆的内接四边形的两条对角线,相交于点,且.
(1)如图,求证:.
(2)在图中找出一组全等的三角形,并给出证明.
(3)如图,圆的半径为,弦于点,当的面积为时,求的长.
【题型3 圆周角定理及其推论的应用】
1.如图,是的外接圆,D是弧的中点,连接,,.平分交于点E.
(1)写出图中一个与相等的角______;
(2)试判断的形状,并说明理由;
(3)若的半径为,,求的长.
2.如图,四边形是的内接四边形,已知,垂足为E,弦的弦心距为.
(1)若,则的度数为 ;
(2)若⊙O的半径为5,,则的长为 .
3.千姿百态的桥
问题:景区计划在半径为的人工湖上修建景观桥,为容纳更多游客赏景休闲,需要景观桥长度最大.现有以下三种设计方案,分别求出每种设计方案中桥长的最大值,景观桥的宽度忽略不计.
“型”
(1)如图①,若点,,,在上,则的最大值为 ;
“型”
(2)如图②,若点,,在上,且.求的最大值;
“型”
(3)如图③,若点,,在上,且,垂足为,则的最大值为 .
4.如图,是的直径,点C是的中点,弦分别交于点F,G,且,连接.
(1)设,用含的式子表示的度数;
(2)求证:;
(3)若的半径为1,记的面积分别为,,S,设,,且满足,求a,b的值.
【题型4 巧用圆内接四边形的性质求解】
1.已知,为的位于圆心两侧的两条弦,且.
(1)如图1,连接,.求证:.
(2)如图2,过点作的垂线交于点.若在上取一点,使得.求证:,,三点共线.
2.如图,均是上的点,且是的直径,若,则的度数是( )
A. B. C. D.
3.如图,是圆内接四边形的一条对角线,点D关于的对称点E在边上,若,则 °.
4.如图所示,圆内接四边形的对角线,交于点,平分,.
如图,圆内接四边形ABCDABCD的对角线ACAC,BDBD交于点EE,BDBD平分∠ABC∠ABC,∠BAC=∠AD
(1)求证:平分,并求的大小;
(2)过点作交的延长线于点,若,,试求四边形的面积和此圆半径的长.
【题型5 切线的判定】
1.如图,是的直径,点C、D在圆上,,平分,与相交于点E.
(1)在的延长线上找一点F,使,连接(要求:尺规作图,不写作法,保留作图痕迹);
(2)求证:是的切线.
2.如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
3.如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
4.如图,是的外接圆,是的直径,的延长线与过点的直线相交于点,且.
(1)求证:是的切线;
(2)点是弧的中点,点在弧上,过点作于点,是否存在常数,使?若存在,求出的值;若不存在,请说明理由.
【题型6 切线的性质】
1.如图,为四边形的外接圆,是等边三角形,是的切线,D是的中点,的延长线交于点E.
(1)求证:;
(2)若,求的面积.
2.已知为的直径,为上一点,.
(1)如图①,点是弧上一点,求的大小;
(2)如图②,过点作的切线,过点作于点,与交于点,若,求的长.
3.如图,在四边形中,平分.点O在上,以点O为圆心,为半径,作与相切于点B,延长线交于点E,交于点F,连接,.
(1)求证:是的切线;
(2)若,求的长.
4.如图,是的直径,B、C都是上的点,连接,E是延长线上一点,连接,且.
(1)证明:是的切线;
(2)连接,交于点F.当时,若,求的长.
【题型7 切线长定理】
1.如图,中,,点D在边上,以为直径的与直线相切于点E,连接,且.连接交于点F.
(1)求证:.
(2)若,求线段的长.
2.如图,圆的圆心在梯形的底边上,并与其它三边均相切,若,,,则长( )
A. B. C. D.无法确定
3.如图,为半圆O的直径,C为半圆弧的三等分点,过B,C两点的半圆O的切线交于点P,若的长是,则的长是 .
4.数学兴趣小组的同学在探究等分问题的过程中,得到了很多成果.
成果一:制作了三分角仪.图(1)是示意图,点在半径的延长线上,,,足够长.若要将三等分,只需要适当放置三分角仪,使点在上,点落在上,当与半相切时,、就将三等分了.
成果二:创造了只用圆规将圆四等分的方法.如图(2),具体步骤为:①将六等分,等分点分别是点、、、、、;②分别以点、为圆心,长为半径作弧,交于点;③以点为圆心,长为半径作弧,交于点、,则点、、、将四等分.
(1)请你说明三分角仪的正确性;
(2)证明点、、、是四等分点.
【题型8 三角形的外接圆与内切圆】
1.如图,是圆O直径,弦,垂足为D,圆O周长为,
(1),求内切圆的面积;
(2),求证:.
2.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
3.如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
4.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;
(2)求证:DE=DB.
【题型9 正多边形和圆的有关计算】
1.在圆内接正六边形中,,分别交于点H,G.
(1)如图①,求证:点H,G三等分.
(2)如图②,操作并证明.
①尺规作图:过点O作的垂线,垂足为K,以点O为圆心,的长为半径作圆;(在图②中完成作图,保留作图痕迹,不需要写作法)
②求证:是①所作圆的切线.
2.如图,正五边形内接于,点在上,则的度数为( )
A. B. C. D.
3.如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
4.如图所示,已知正八边形内接于,连接、,相交于点.若的半径为1,
(1)求的长;
(2)求的度数.
【题型10 正多边形中的规律探究性问题】
1.观察下列结论:
(1)如图①,在正三角形中,点M,N是上的点,且,则,;
(2)如图②,在正方形中,点M,N是上的点,且,则,;
(3)如图③,在正五边形中,点M,N是上的点,且,则,;……
根据以上规律,在正n边形中,对相邻的三边实施同样的操作过程,即点M,N是上的点,且,与相交于O.也会有类似的结论.你的结论是 .
2.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
3.如图1,图2,图3 ,M、N分别是的内接正三角形,正方形,正五边形,…的边上的点,且,连接,图1中,图2中,图3中…,根据这样的规律,图n中的度数是 .
4.李老师带领班级同学进行拓广探索,通过此次探索让同学们更深刻的了解的意义.
(1)[定义]我们将正n边形的周长L与正多边形对应的内切圆的周长C的比值,称作这个正n边形的“正圆度”.如图,正三角形的边长为1,求得其内切圆的半径为,因此___________;
(2)[探索]分别求出正方形和正六边形的“正圆度”;
(3)[总结]随着n的增大,具有怎样的规律,试通过计算,结合圆周率的诞生,简要概括.
【题型11 圆锥侧面展开图的有关计算】
1.如图, ,点A、C分别在射线上, .
(1)用尺规在图中作一段劣弧,使得它在A、C两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)将劣弧所在的扇形围成圆锥的侧面,则该圆锥的底面圆的半径为 .
(3)求所得的劣弧与线段围成的封闭图形的面积.
2.如图,在直径为2的圆形纸片上裁剪出圆心角的扇形.
(1)求阴影部分面积;
(2)用所裁剪的扇形纸片围成一个圆锥的侧面,求圆锥底面圆的半径.
3.如图,在半径为4的扇形中,,点C是上的一个动点(不与点A,重合),连接,,,,垂足分别为点D,E.
(1)若扇形是一个圆锥的侧面展开图,求该圆锥的底面半径;
(2)在中是否存在长度为定值的边 若存在,请求出这条边的长度;若不存在,请说明理由.
4.【综合与实践】
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽,
(1)现在需要制作一个,的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
【题型12 不规则图形面积的计算】
1.如图,扇形中,,,点为的中点,将扇形绕点顺时针旋转,得到扇形,则图中阴影部分的面积为( )
A. B.
C. D.
2.如图,在中,,,D是的中点,以点D为圆心,作圆心角为的扇形,点C恰好在上(点E,F不与点C重合),半径,分别与,相交于点G,H,则阴影部分的面积为 .
3.如图,在中,,,点O是边的中点,半圆O与相切于点D、E,若阴影部分的面积为,则的长为( )
A. B. C.2 D.
4.如图,是的内接三角形,是的直径,,,弦于,点是延长线上一点,且,连接.
(1)填空: °;
(2)判断与的位置关系,并说明理由;
(3)取的中点,连接,求图中阴影部分的面积.
【题型13 利用弧长和扇形面积公式解决几何图形的旋转问题】
1.如图,在等边内有一点,且,,,若把绕着点逆时针旋转得到,连接,.
(1)求的度数;
(2)求的长.
(3)求点划过的路径长;
(4)当时,如果是由旋转所得,求扫过的区域的面积.
2.如图,已知正方形的边长为cm,将正方形在直线上顺时针连续翻转4次,则点所经过的路径长为 ( )
A.4πcm B.πcm C.πcm D.πcm
3.如图,在矩形中,已知,将矩形绕着点在桌面上顺时针旋砖至,使其停靠在矩形的点处,若,则点的运动路径长为( )
A. B. C. D.
4.如图①,小慧同学把一个等边三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120°,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°,……,按上述方法经过若干次旋转后,她提出了如下问题:
(1)若正方形纸片OABC按上述方法经过3次旋转,求顶点O经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形OABC按上述方法经过5次旋转,求顶点O经过的路程;
(2)正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是?
参考答案
【题型1 垂径定理的应用】
1.(1)解:如图,连接,.
∵是的中点,,
∴,所在的直线经过圆心.
设半径,则.
∵在中,,
∴,解得.
答:主桥拱所在圆的半径长为5米.
(2)(2)如图,设与相交于点.
由题意得.
∵,∴.
∵,
∴,∴.
∵在中,,
∴,
∴.
答:此时水面的宽度约为9米.
2.解:由题可知,
∵为半径,
∴尺寸,
设,
∵,
∴,
在中,
由勾股定理得,
解得,
∴这根圆形木材的直径为26寸.
3.解:设该圆材的半径为寸.
如图所示,过点作 于点,交于点,连接,
则寸,
设寸,尺寸,
所以 寸.
在中,
即
解得,
则,即该圆材的直径为寸.
4.(1)解:如图,连接.
,
,
,
,
,
直径小于长度;
(2)解:如图,过点O作交于点C,
在中,,,
,
,
,
水的最大深度为.
【题型2 弧、弦、圆心角的关系】
1.(1)证明:∵,
∴
∴,
即.
∴.
(2)证明:连接
∵
∴
∴
∴
∵
∴E、O都在的垂直平分线上.
∴
2.证明:连接.
在中, ,
,
,、分别是半径和的中点,
,
,
,
.
3.证明:∵,,
∴,,
∴,
∴.
4.(1)证明:∵,
∴,
∴,
即,
∴,
即,
∴;
(2)解:.
证明:由()得,,
在和中,
,
∴;
(3)解:如图,连接,
∵,
∴,
同理()可得,
∴为等腰直角三角形,
∴,
∴,
∴,
设,,
在中,由勾股定理得,
∴,
又∵的面积为,
∴,
∴,
∴,
∴,
∴.
【题型3 圆周角定理及其推论的应用】
1.(1)解:∵D是弧的中点,
∴,
∴,
故答案为:(或或);
(2)解:是等腰三角形,
理由如下:
∵点D是的中点,
∴,
∴,
又∵CE平分,
∴,
在中,,
∵,
∴,
∴,
即是等腰三角形.
(3)解:连接OD,交AC于点F,连接OA.如图,
∵,D是弧AC的中点,
∴,,
∵,
∴,
在中,,
∴,
又,
∴。
2. 6
【分析】(1)连接,证明和都是等腰直角三角形即可;
(2)延长交于点,连接,则是的中位线,可以求出,然后根据垂直证明,根据圆周角相等则所对的弦相等得到.
【详解】解:(1)如图,连接,
是弦的弦心距,
,
和都是等腰直角三角形,
∵,
,
故答案为:;
(2)如图,延长交于点,连接,
由,得是的中位线,
,
在中,,
由勾股定理得
,
,
∵是的直径,
∴,
,
∵
∴,
,
故答案为:6.
3.解:(1)∵点,,,在半径为的上,
∴,,
∴,
∴的最大值为,
故答案为:;
(2)连接,过点作于点,
∵,的半径为,
∴,
∴,
∵,
即当时,的面积取得最大值,
∴,即,
∴,
∴的最大值为;
(3)如图,过点作于点,延长交于点,过点作于点,连接,,设,,
∵,
∴,
∴四边形是矩形,
∴,
∴,当点与点重合时,取“”,
∵,
,
∴,
∵,即,
整理,得:,
∴,
解得:,
∴,
∴
,
∴的最大值为
故答案为:.
4.(1)连接,,
∵是的直径,点C是的中点,
∴,,
∴,
∵,
∴,
∴;
(2)把顺时针旋转,点对应点,连接,则,
∵,
∴与重合,
∴,
∴,,,
∴,
∴,
∵,,
∴,
∵,,
∴,
∴,
∴;
(3)∵的半径为1,
∴,
∵点C是的中点,
∴,
∵,,
∴,
∴,,,
由(2)可得,,,
∴,,
∵,
∴,
∴,
∵,
∴,
整理得,即,
∴
∴,即
∵,
∴,
∴
整理可得,解得,
∵,
∴,
∴.
【题型4 巧用圆内接四边形的性质求解】
1.(1)证明: ,
,
,
,
;
(2)如图2,连接,,,,
,
,
,
,
,
,
,
,
,
经过圆心.
∴,,三点共线
2.B
【分析】本题主要考查圆与内接四边形的综合,掌握内接四边形的性质,直径所对圆周角是直角的知识是解题的关键.
根据均是上的点,可得四边形是内接四边形,则,由此可求出的度数,根据是的直径,可得,由此即可求解.
【详解】解:均是上的点,
∴四边形是内接四边形,
∴,
∵,
∴,
∴,
∵是的直径,
∴,
∴,
故选:B.
3.110
【分析】本题考查了圆内接四边形的性质定理,轴对称的性质,熟练掌握圆内接四边形的性质定理及轴对称的性质是解题的关键.根据圆内接四边形的性质定理可得,再根据轴对称的性质即得答案.
【详解】四边形是圆内接四边形,,
,
点D关于的对称点E在边上,
,
.
故答案为:110.
4.(1)证明:,,
,
平分,
平分,
,
四边形是圆内接四边形,
,
,
,
,
;
(2)解:,,
,
,
,
是圆的直径,
垂直平分,
,
,
是等边三角形,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
,
,,
,
是圆的直径,
圆的半径长是4,
.
【题型5 切线的判定】
1.(1)解:根据题意,作图如下:
则点、为所求.
(2)证明:连接.
是的直径,
,
平分,
,
,
,
,
.
,
,
,
,
,
.
,,
,
,
,
.
又为半径,
是切线.
2.解:与相切.
证明:连接.
∵,
∴.
∵图形沿过点A的直线翻折,点C的对应点落在边上,
∴.
∴.
∴.
∴由,得,即.
∴与相切.
3.(1)解:是的切线,理由如下,
连接,
是圆的直径,
,
,
,
,
,
,
,
半径,
是的切线;
(2)解:连接,
,
,
等边三角形,
,
为的中点,
,
.
故答案为:30.
4.(1)∵是的直径,
∴,
∵,,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解: 存在,,理由如下:
在上取一点,使得,连接,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∵是的直径,
∴,
∵,,
∴,
∴,
∴,
∴.
【题型6 切线的性质】
1.(1)证明:是等边三角形,
.
连接,
∵
则.
是的切线,
.
.
.
.
(2)解:为四边形的外接圆,.
是的中点,
∴
.
∴为直角三角形.
.
.
的面积为.
2.(1)解:连接,
为的直径,,
,
是等边三角形,
,
;
(2)解:连接,与相交于,
是的切线,
,
,
,
,
,
为的直径,
,
,
,
,
.
3.(1)证明:如图,连接.
为圆O的切线,
.
平分,
.
,
,
,,
.
在和中,
,
,
.
是的切线.
(2)解:,
,
,
.
.
是直径,
,
,
.
在中,,,
.
.
4.(1)证明: ,,
,
是的直径,
,
,
,
,
,即,
是半径,
是的切线;
(2)解: ,
,
,
,
是等边三角形,
,
,
,
,
,
,
,
.
【题型7 切线长定理】
1.(1)解:如下图,连接,
与相切于点E,
,
,
,
,
是的半径,,
与相切于点C,
,
在和中,,
,
,
,
;
(2),
,
,
,
,且,
,
解得:,
,
,
点O、点A都在线段的垂直平分线上,
垂直平分,
,
,
,
,
线段,的长分别是1、.
2.A
【分析】此题主要考查了切线的性质和等腰三角形的性质,利用切线的性质得出,进而得出,即可得出,同理:即可得出结论.
【详解】连接,,
,是的切线,
,
∵,
,
,
,
,
,
,
,
同理可得:,
故选:A.
3.
【分析】本题主要考查的知识点是:圆心角、假、张的关系,切线的性质,切线长定理以及解直角三角形的应用等知识,连接,由于C是半圆的三等分点,那么,进而可由切线长定理求得;在中根据半径的长以及的度数,可求得的值,进而可由勾股定求得的长.
【详解】解:连接,
∵C为半圆弧的三等分点,
∴,
∵,都是的切线,
∴,
在中,,则,
在中,由勾股定理得:,
故答案为:
4.(1)证明:∵,
即垂直平分,
∴,
∵,
∴平分,
∴,
∵,
∴为的切线,
∵与半相切,
∴平分,
∴,
即将三等分;
(2)如图2
∵是的直径,
∴
∵,.
∴,
设的半径为,
在中,,
∴,
∵,
∴,
∴,
在中,,
∴,
在中,,
∴是直角三角形且,
∴,
∴点、、、是的四等分点.
【题型8 三角形的外接圆与内切圆】
1.(1)解:连接,
∵是圆O直径,圆O周长为,
∴,,
∴,
∵
∴,
∵是圆O直径,弦,
∴,垂直平分,
∴,
∴是等边三角形,
∴,点O是的内心,
∴,
∴
∴内切圆的面积为;
(2)如图,连接,
∵是等边三角形, ,
∴,,
∴,
∵点O是的内心,
∴,
∴
∴.
2.(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
3.(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,则EM=EN,
∵∠BAE=∠CAE,
∴=,
∴BE=EC=4.
∵AE=AE,EM=EN,
∴△AEM≌△AEN,
∴AM=AN.
∵BE=EC,EM=EN,
△BME≌△CNE(HL),
∴BM=CN.
设BM为x,则8-x=6+x,解得x=1,即BM=1,
∴AM=7.
又∵BE=4,由勾股定理得,EM==.
∴AE==8,
∵EI=BE=4,
∴AI=AE EI=4.
4.(1)解:∵∠CBD=34°
∴∠CAD=34°
∵点E是△ABC的的内心
∴∠BAC=2∠CAD=68°
∴∠EBC+∠ECB=(180°-68°)÷2=56°
∴∠BEC=180°-56°=124°
(2)∵E是△ABC的内心
∴∠BAD=∠CAD,∠EBA=∠EBC
∵ ∠DEB=∠BAD+∠EBA,∠DBE=∠EBC+∠CBD,∠CBD=∠CAD
∴∠DEB=∠DBE
∴DE=DB .
【题型9 正多边形和圆的有关计算】
1.(1)证明:在圆内接正六边形中,
,
∴,
∴.
在和中,
,
∴.
∴.
∴是等边三角形,
∴.
∴点H,G三等分.
(2)①解:如图,即为所求作.
②证明:如图,过点O作,垂足为P,连接,则.
由(1)知,,
∴.
∵,,
∴.
∴是①所作圆的切线.
2.D
【分析】本题主要考查了正多边形和圆,圆内接四边形的性质,熟记圆内接四边形的对角互补是解决问题的关键.
先由正多边形内角和定理求出,再根据圆内接四边形的性质即可求出.
【详解】解:正五边形内接于,
,
四边形是内接四边形,
,
,
故选:D.
3. 4
【分析】本题考查了正多边形与圆,掌握圆的相关性质及正方形的相关性质、准确的辅助线及计算是本题的解题关键.
(1)利用圆的面积公式计算出半径即可求出直径;
(2)连接,,以、为边作,连接,证明出,,当、、共线时,最小,即为的最小值,利用勾股定理求出即可解答此问.
【详解】解:(1)的面积为,
,
的直径长为,
故答案为:;
(2)如图,连接,,以、为边作,连接,
四边形为正方形,
,,
四边为平行四边形,
,
,
,
当、、共线时,最小,即为的最小值,
在中,,,
,
,
,
周长的最小值为,
故答案为:4.
4.(1)解:如图,连接,,与交于点,
由题意可知,,,
∵多边形是正八边形,
∴,
∴,
∴,
∴;
(2)∵所对的圆心角为,
∴所对的圆周角为,
∵,
∴.
【题型10 正多边形中的规律探究性问题】
1. ,
【分析】根据正多边形内角和定理结合全等三角形的判定和性质可得出(1)、(2)、(3)的结论,根据以上规律可得出正n边形的结论.
【详解】(1)∵正三角形ABC中,点M、N是AB、AC边上的点,且AM=BN,
∴AB=AC,∠CAM=∠ABN=,
∵在△ABN和△CAM中,
,
∴△ABN≌△CAM(SAS),
∴AN= CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA =∠OAC+∠BAN =∠BAC=60°,
故结论为:AN= CM,∠NOC=60;
(2)∵正方形ABCD中,点M、N是AB、BC边上的点,且AM=BN,
∴AB=AD,∠DAM=∠ABN=,
同理可证:Rt△ABNRt△DAM,
∴AN= DM,∠BAN=∠ADM,
∠NOD=∠OAD+∠ADM =∠OAD+∠BAN =∠BAC=90°,
故结论为:AN= DM,∠NOD=90;
(3)∵正五边形ABCDE中,点M、N是AB、BC边上的点,且AM=BN,
∴AB=AE,∠EAM=∠ABN=,
同理可证得:Rt△ABNRt△EAM,
∴AN= EM,∠BAN=∠AEM,
∠NOE=∠OAE+∠AEM =∠OAE+∠BAN =∠BAE=108°,
故结论为:AN= EM,∠NOE=108;
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
∴以上所求的角恰好等于正n边形的内角,
在正n边形中,点M,N是上的点,且,与相交于O,结论为: ,.
故答案为: ,.
2.D
【详解】解:连结OE1,OD1,OD2,如图,根据正六边形的性质得∠E1OD1=60°,则△E1OD1为等边三角形,再根据切线的性质得OD2⊥E1D1,于是可得OD2=E1D1=×2,利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=×2,同理可得正六边形A3B3C3D3E3F3的边长=()2×2,依此规律可得正六边形A10B10C10D10E10F10的边长=()9×2=,
故选:D,
3.
【分析】作多边形的半径,根据多边形的性质可证,得,再根据“等边对等角”得,于是可得,从而可证则,因此.
本题考查了正多边形的性质、全等三角形的判定和性质、等边对等角、正多边形中心角等知识点,解题的关键综合运用这些性质解题.
【详解】不失一般性,设时的情形,可以推广到一般情况.连接,如下图
由正多边形的性质知:
∴
∴
由得:
∴
即:
又∵
∴
∴
∴
即:
∵
∴
故答案为:.
4.(1)解:由题意得,,
故答案为:;
(2)解:假设正方形边长1,
∴此时正方形的内切圆半径为,
∴;
设正六边形的边长为1,内切圆圆心为O,则,
又∵,
∴是等边三角形,
∴,
∴,
∴;
(3)解:,随着n的增大,越来越接近于1.由张衡、祖冲之的研究,精进的取值的方法可知:正多边形,边长数越多,越接近于圆,因此当边长增多时,其周长L也与对应的内切圆周长更接近,其比值更接近于1.
【题型11 圆锥侧面展开图的有关计算】
1.(1)解:如图,过A、分别作、的垂线,它们相交于,然后以为半径作,
则即为所求;
(2)解:∵,,
,
由作图知
和分别是切线,
,
,
为等边三角形,
则长为:,
所在的扇形围成圆锥的侧面,则该圆锥的底面圆的半径设为r,
,
,
则该圆锥的底面圆的半径设为;
(3)∵,,
,
由作图知
和分别是切线,
,
,
为等边三角形,
,,
∵,
垂直平分,
平分,
,
,
劣弧与线段、围成的封闭图形的面积
.
2.(1)解:连接,
∵,
∴是圆O的直径,
∴点A、O、B三点共线,
∴,
又∵,
∴,
∵圆的直径为2,
则,
故.
∴;
(2)解:的长,
则,
解得:.
故该圆锥的底面圆的半径是.
3.(1)解:设该圆锥的底面半径为r,
由题意得.
解得,
即该圆锥的底面半径为1.
(2)存在,的长为定值.如图,连接.
∵,,
∴D为中点,E为中点.
∴为的中位线.
∴.
∵,,
∴.
∴.
4.(1),,
,
,
扇形纸板的圆心角度数为;
(2)如图所示.连接,过点P作,线段就是彩带长度的最小值,
由(1)得,
彩带长度的最小值为.
【题型12 不规则图形面积的计算】
1.B
【分析】过点作于点,过点作交的延长线于点,设交于点,交于点,根据题意得出,进而根据即可求解.
【详解】解:如图所示,过点作于点,过点作交的延长线于点,设交于点,交于点,
∵
则四边形是正方形,
,
∴,
,
,
,
在中,,
,
,
,
∴,
,
,
,
,
故选:B.
【点睛】本题考查了求扇形面积,旋转的性质,正方形的性质,掌握扇形面积公式是解题的关键.
2.
【分析】本题考查正方形的判定和性质,全等三角形的判定和性质,扇形的面积,作辅助线构造全等三角形是解问题的关键.
连接,过点D作于点M,过点D作于点N,先证明是正方形,然后证明,最后运用解题即可.
【详解】如图,连接,过点D作于点M,过点D作于点N,
则
∵,
∴,,四边形是矩形
∵,D是的中点,
∴
∴
同理
∴四边形是正方形
∴,
由题可知,,
∴
在与中,
,
∴
∴
∵
∴
故答案为
3.C
【分析】连接,根据切线长定理和切线的性质可知四边形是正方形,从而证明,由等腰直角三角形的性质推出,从而证明,利用平行线间距离相等从而得到,继而得到阴影部分的面积等于扇形的面积,从而利用得到扇形半径的长度,从而得到的长,继而得出的长.
【详解】解:连接,
∵半圆O与相切于点D、E,
∴,.
∵,
∴四边形是矩形,
又∵,
∴四边形是正方形.
∴,.
又∵,,点O是边的中点,
∴,,
∴.
∵,,
∴.
∵平行线间距离相等,
∴,
∴阴影部分的面积等于扇形的面积.
∵阴影部分的面积为,
∴,
∴,
∴,
∴.
故选:C.
4.(1)解:弦于,是的直径,
,
,
故答案为:30;
(2)解:与相切,
理由如下:
连接,如图所示:
弦于,是的直径,
,,
,
,
,
,
,
,
是的半径,
与相切;
(3)解:是的直径,
,
,,
,
,
连接,如图所示:
点是的中点,
,
,
是的中位线,
,,
,
,
,
图中阴影部分的面积的面积扇形的面积的面积.
【题型13 利用弧长和扇形面积公式解决几何图形的旋转问题】
1.(1)解:把绕着点逆时针旋转得到,则是等边三角形,
,
是等边三角形,
,
,
,
在和中,
,
,,
在中,,,,则,由勾股定理的逆定理可知为直角三角形,且,
;
(2)解:把绕着点逆时针旋转得到,则是等边三角形,
;
(3)解:如图所示:
把绕着点逆时针旋转得到,点划过的路径是,则长度为;
(4)解:由(1)的证明过程可知,,点划过的路径是,点划过的路径是,如图所示:
由旋转性质可知,
扫过的区域的面积
.
2.B
【分析】正方形 在直线上顺时针连续翻转4次,实际点经过的路径有三段,其中一段以为半径,圆心角为的弧长,另两段是以为半径,圆心角为的弧长,然后根据弧长公式计算.
【详解】解:点经过的路径如图
因为正方形 的边长为,
所以,
所以点所经过的路径长.
故选:B.
3.B
【分析】本题考查了旋转的性质、弧长的计算、轨迹等知识,由在矩形中,已知,可求得的长,由旋转的性质,易得,又由,即可求得的度数,继而求得答案.
【详解】解:连接,
∵在矩形中,,
,
,
根据旋转的性质可知:,
根据矩形的性质可知:,
,
,
,
∴点的运动路径长为: .
故选B.
4.解:(1)如图所示,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段弧,即弧OO1、弧O1O2以及弧O2O3,
∴ 顶点O运动过程中经过的路程为:
,
顶点O在此运动过程中所形成的图形与直线l2围成图形的面积为:
=1+π,
正方形OABC经过5次旋转,顶点O经过的路程为:
.
(2)∵ 正方形OABC经过3次旋转,顶点O经过的路程为:
,
根据第四次正方形旋转O点不动,也就是此时也是正方形OABC经过4次旋转的路程,
∴ π=10×π+π,
∴正方形纸片OABC经过了:10×4+1=41次旋转.
【题型1 垂径定理的应用】
1.如图,一座石桥的主桥拱是四弧形,某时刻添得水面的宽度为8米,拱高(的中点C到水面的距离)为2米.
(1)求主桥拱所在圆的半径.
(2)在主桥拱所在圆的圆心处有一水位检测仪,若过几天某时刻的水面为,检测仪观测点的仰角为,求此时水面的宽度.(参考数据:,,)
2.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.如图,用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).这根圆柱形木材的直径是多少寸?
3.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一类似问题“今有圆材埋在壁中,不知大小.以锯锯之,深两寸,锯道长一尺二,问径几何 ”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为寸,锯道尺(尺寸),求该圆材的直径为多少寸
4.如图,装有水的水槽放在水平桌面上,其横截面是以为直径的半圆O,,为桌面截线,水面截线,直径一端点B刚好与点N重合,.
(1)计算的长度,并比较直径与长度的大小;
(2)请在图中画出线段,用其长度表示水的最大深度,并求水的最大深度.
【题型2 弧、弦、圆心角的关系】
1.如图,、是的两条弦,与相交于点E,.
(1)求证:;
(2)连接 作直线求证:.
2.如图,,D,E分别是半径,的中点.求证:.
3.已知,如图,在中,,,求证:.
4.已知是圆的内接四边形的两条对角线,相交于点,且.
(1)如图,求证:.
(2)在图中找出一组全等的三角形,并给出证明.
(3)如图,圆的半径为,弦于点,当的面积为时,求的长.
【题型3 圆周角定理及其推论的应用】
1.如图,是的外接圆,D是弧的中点,连接,,.平分交于点E.
(1)写出图中一个与相等的角______;
(2)试判断的形状,并说明理由;
(3)若的半径为,,求的长.
2.如图,四边形是的内接四边形,已知,垂足为E,弦的弦心距为.
(1)若,则的度数为 ;
(2)若⊙O的半径为5,,则的长为 .
3.千姿百态的桥
问题:景区计划在半径为的人工湖上修建景观桥,为容纳更多游客赏景休闲,需要景观桥长度最大.现有以下三种设计方案,分别求出每种设计方案中桥长的最大值,景观桥的宽度忽略不计.
“型”
(1)如图①,若点,,,在上,则的最大值为 ;
“型”
(2)如图②,若点,,在上,且.求的最大值;
“型”
(3)如图③,若点,,在上,且,垂足为,则的最大值为 .
4.如图,是的直径,点C是的中点,弦分别交于点F,G,且,连接.
(1)设,用含的式子表示的度数;
(2)求证:;
(3)若的半径为1,记的面积分别为,,S,设,,且满足,求a,b的值.
【题型4 巧用圆内接四边形的性质求解】
1.已知,为的位于圆心两侧的两条弦,且.
(1)如图1,连接,.求证:.
(2)如图2,过点作的垂线交于点.若在上取一点,使得.求证:,,三点共线.
2.如图,均是上的点,且是的直径,若,则的度数是( )
A. B. C. D.
3.如图,是圆内接四边形的一条对角线,点D关于的对称点E在边上,若,则 °.
4.如图所示,圆内接四边形的对角线,交于点,平分,.
如图,圆内接四边形ABCDABCD的对角线ACAC,BDBD交于点EE,BDBD平分∠ABC∠ABC,∠BAC=∠AD
(1)求证:平分,并求的大小;
(2)过点作交的延长线于点,若,,试求四边形的面积和此圆半径的长.
【题型5 切线的判定】
1.如图,是的直径,点C、D在圆上,,平分,与相交于点E.
(1)在的延长线上找一点F,使,连接(要求:尺规作图,不写作法,保留作图痕迹);
(2)求证:是的切线.
2.如图,将沿过点的直线翻折并展开,点的对应点落在边上,折痕为,点在边上,经过点、.若,判断与的位置关系,并说明理由.
3.如图,是的内接三角形,是的直径,为的中点,,在的延长线上.
(1)是的切线吗?为什么?
(2)若,则的度数为______°.
4.如图,是的外接圆,是的直径,的延长线与过点的直线相交于点,且.
(1)求证:是的切线;
(2)点是弧的中点,点在弧上,过点作于点,是否存在常数,使?若存在,求出的值;若不存在,请说明理由.
【题型6 切线的性质】
1.如图,为四边形的外接圆,是等边三角形,是的切线,D是的中点,的延长线交于点E.
(1)求证:;
(2)若,求的面积.
2.已知为的直径,为上一点,.
(1)如图①,点是弧上一点,求的大小;
(2)如图②,过点作的切线,过点作于点,与交于点,若,求的长.
3.如图,在四边形中,平分.点O在上,以点O为圆心,为半径,作与相切于点B,延长线交于点E,交于点F,连接,.
(1)求证:是的切线;
(2)若,求的长.
4.如图,是的直径,B、C都是上的点,连接,E是延长线上一点,连接,且.
(1)证明:是的切线;
(2)连接,交于点F.当时,若,求的长.
【题型7 切线长定理】
1.如图,中,,点D在边上,以为直径的与直线相切于点E,连接,且.连接交于点F.
(1)求证:.
(2)若,求线段的长.
2.如图,圆的圆心在梯形的底边上,并与其它三边均相切,若,,,则长( )
A. B. C. D.无法确定
3.如图,为半圆O的直径,C为半圆弧的三等分点,过B,C两点的半圆O的切线交于点P,若的长是,则的长是 .
4.数学兴趣小组的同学在探究等分问题的过程中,得到了很多成果.
成果一:制作了三分角仪.图(1)是示意图,点在半径的延长线上,,,足够长.若要将三等分,只需要适当放置三分角仪,使点在上,点落在上,当与半相切时,、就将三等分了.
成果二:创造了只用圆规将圆四等分的方法.如图(2),具体步骤为:①将六等分,等分点分别是点、、、、、;②分别以点、为圆心,长为半径作弧,交于点;③以点为圆心,长为半径作弧,交于点、,则点、、、将四等分.
(1)请你说明三分角仪的正确性;
(2)证明点、、、是四等分点.
【题型8 三角形的外接圆与内切圆】
1.如图,是圆O直径,弦,垂足为D,圆O周长为,
(1),求内切圆的面积;
(2),求证:.
2.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
3.如图,O是△ABC的外心,I是△ABC的内心,连接AI并延长交BC和⊙O于D,E.
(1)求证:EB=EI;
(2)若AB=8,AC=6,BE=4,求AI的长.
4.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BE,
(1)若∠CBD=34°,求∠BEC的度数;
(2)求证:DE=DB.
【题型9 正多边形和圆的有关计算】
1.在圆内接正六边形中,,分别交于点H,G.
(1)如图①,求证:点H,G三等分.
(2)如图②,操作并证明.
①尺规作图:过点O作的垂线,垂足为K,以点O为圆心,的长为半径作圆;(在图②中完成作图,保留作图痕迹,不需要写作法)
②求证:是①所作圆的切线.
2.如图,正五边形内接于,点在上,则的度数为( )
A. B. C. D.
3.如图,正方形内接于,线段在对角线上运动,若的面积为,,则(1)的直径长为 ;(2)周长的最小值是 .
4.如图所示,已知正八边形内接于,连接、,相交于点.若的半径为1,
(1)求的长;
(2)求的度数.
【题型10 正多边形中的规律探究性问题】
1.观察下列结论:
(1)如图①,在正三角形中,点M,N是上的点,且,则,;
(2)如图②,在正方形中,点M,N是上的点,且,则,;
(3)如图③,在正五边形中,点M,N是上的点,且,则,;……
根据以上规律,在正n边形中,对相邻的三边实施同样的操作过程,即点M,N是上的点,且,与相交于O.也会有类似的结论.你的结论是 .
2.如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. B. C. D.
3.如图1,图2,图3 ,M、N分别是的内接正三角形,正方形,正五边形,…的边上的点,且,连接,图1中,图2中,图3中…,根据这样的规律,图n中的度数是 .
4.李老师带领班级同学进行拓广探索,通过此次探索让同学们更深刻的了解的意义.
(1)[定义]我们将正n边形的周长L与正多边形对应的内切圆的周长C的比值,称作这个正n边形的“正圆度”.如图,正三角形的边长为1,求得其内切圆的半径为,因此___________;
(2)[探索]分别求出正方形和正六边形的“正圆度”;
(3)[总结]随着n的增大,具有怎样的规律,试通过计算,结合圆周率的诞生,简要概括.
【题型11 圆锥侧面展开图的有关计算】
1.如图, ,点A、C分别在射线上, .
(1)用尺规在图中作一段劣弧,使得它在A、C两点分别与射线和相切.要求:写出作法,并保留作图痕迹;
(2)将劣弧所在的扇形围成圆锥的侧面,则该圆锥的底面圆的半径为 .
(3)求所得的劣弧与线段围成的封闭图形的面积.
2.如图,在直径为2的圆形纸片上裁剪出圆心角的扇形.
(1)求阴影部分面积;
(2)用所裁剪的扇形纸片围成一个圆锥的侧面,求圆锥底面圆的半径.
3.如图,在半径为4的扇形中,,点C是上的一个动点(不与点A,重合),连接,,,,垂足分别为点D,E.
(1)若扇形是一个圆锥的侧面展开图,求该圆锥的底面半径;
(2)在中是否存在长度为定值的边 若存在,请求出这条边的长度;若不存在,请说明理由.
4.【综合与实践】
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽,
(1)现在需要制作一个,的生日帽,请帮忙计算出所需扇形纸板的圆心角度数;
(2)为了使(1)中所制作的生日帽更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),求彩带长度的最小值.
【题型12 不规则图形面积的计算】
1.如图,扇形中,,,点为的中点,将扇形绕点顺时针旋转,得到扇形,则图中阴影部分的面积为( )
A. B.
C. D.
2.如图,在中,,,D是的中点,以点D为圆心,作圆心角为的扇形,点C恰好在上(点E,F不与点C重合),半径,分别与,相交于点G,H,则阴影部分的面积为 .
3.如图,在中,,,点O是边的中点,半圆O与相切于点D、E,若阴影部分的面积为,则的长为( )
A. B. C.2 D.
4.如图,是的内接三角形,是的直径,,,弦于,点是延长线上一点,且,连接.
(1)填空: °;
(2)判断与的位置关系,并说明理由;
(3)取的中点,连接,求图中阴影部分的面积.
【题型13 利用弧长和扇形面积公式解决几何图形的旋转问题】
1.如图,在等边内有一点,且,,,若把绕着点逆时针旋转得到,连接,.
(1)求的度数;
(2)求的长.
(3)求点划过的路径长;
(4)当时,如果是由旋转所得,求扫过的区域的面积.
2.如图,已知正方形的边长为cm,将正方形在直线上顺时针连续翻转4次,则点所经过的路径长为 ( )
A.4πcm B.πcm C.πcm D.πcm
3.如图,在矩形中,已知,将矩形绕着点在桌面上顺时针旋砖至,使其停靠在矩形的点处,若,则点的运动路径长为( )
A. B. C. D.
4.如图①,小慧同学把一个等边三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120°,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°,……,按上述方法经过若干次旋转后,她提出了如下问题:
(1)若正方形纸片OABC按上述方法经过3次旋转,求顶点O经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形OABC按上述方法经过5次旋转,求顶点O经过的路程;
(2)正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是?
参考答案
【题型1 垂径定理的应用】
1.(1)解:如图,连接,.
∵是的中点,,
∴,所在的直线经过圆心.
设半径,则.
∵在中,,
∴,解得.
答:主桥拱所在圆的半径长为5米.
(2)(2)如图,设与相交于点.
由题意得.
∵,∴.
∵,
∴,∴.
∵在中,,
∴,
∴.
答:此时水面的宽度约为9米.
2.解:由题可知,
∵为半径,
∴尺寸,
设,
∵,
∴,
在中,
由勾股定理得,
解得,
∴这根圆形木材的直径为26寸.
3.解:设该圆材的半径为寸.
如图所示,过点作 于点,交于点,连接,
则寸,
设寸,尺寸,
所以 寸.
在中,
即
解得,
则,即该圆材的直径为寸.
4.(1)解:如图,连接.
,
,
,
,
,
直径小于长度;
(2)解:如图,过点O作交于点C,
在中,,,
,
,
,
水的最大深度为.
【题型2 弧、弦、圆心角的关系】
1.(1)证明:∵,
∴
∴,
即.
∴.
(2)证明:连接
∵
∴
∴
∴
∵
∴E、O都在的垂直平分线上.
∴
2.证明:连接.
在中, ,
,
,、分别是半径和的中点,
,
,
,
.
3.证明:∵,,
∴,,
∴,
∴.
4.(1)证明:∵,
∴,
∴,
即,
∴,
即,
∴;
(2)解:.
证明:由()得,,
在和中,
,
∴;
(3)解:如图,连接,
∵,
∴,
同理()可得,
∴为等腰直角三角形,
∴,
∴,
∴,
设,,
在中,由勾股定理得,
∴,
又∵的面积为,
∴,
∴,
∴,
∴,
∴.
【题型3 圆周角定理及其推论的应用】
1.(1)解:∵D是弧的中点,
∴,
∴,
故答案为:(或或);
(2)解:是等腰三角形,
理由如下:
∵点D是的中点,
∴,
∴,
又∵CE平分,
∴,
在中,,
∵,
∴,
∴,
即是等腰三角形.
(3)解:连接OD,交AC于点F,连接OA.如图,
∵,D是弧AC的中点,
∴,,
∵,
∴,
在中,,
∴,
又,
∴。
2. 6
【分析】(1)连接,证明和都是等腰直角三角形即可;
(2)延长交于点,连接,则是的中位线,可以求出,然后根据垂直证明,根据圆周角相等则所对的弦相等得到.
【详解】解:(1)如图,连接,
是弦的弦心距,
,
和都是等腰直角三角形,
∵,
,
故答案为:;
(2)如图,延长交于点,连接,
由,得是的中位线,
,
在中,,
由勾股定理得
,
,
∵是的直径,
∴,
,
∵
∴,
,
故答案为:6.
3.解:(1)∵点,,,在半径为的上,
∴,,
∴,
∴的最大值为,
故答案为:;
(2)连接,过点作于点,
∵,的半径为,
∴,
∴,
∵,
即当时,的面积取得最大值,
∴,即,
∴,
∴的最大值为;
(3)如图,过点作于点,延长交于点,过点作于点,连接,,设,,
∵,
∴,
∴四边形是矩形,
∴,
∴,当点与点重合时,取“”,
∵,
,
∴,
∵,即,
整理,得:,
∴,
解得:,
∴,
∴
,
∴的最大值为
故答案为:.
4.(1)连接,,
∵是的直径,点C是的中点,
∴,,
∴,
∵,
∴,
∴;
(2)把顺时针旋转,点对应点,连接,则,
∵,
∴与重合,
∴,
∴,,,
∴,
∴,
∵,,
∴,
∵,,
∴,
∴,
∴;
(3)∵的半径为1,
∴,
∵点C是的中点,
∴,
∵,,
∴,
∴,,,
由(2)可得,,,
∴,,
∵,
∴,
∴,
∵,
∴,
整理得,即,
∴
∴,即
∵,
∴,
∴
整理可得,解得,
∵,
∴,
∴.
【题型4 巧用圆内接四边形的性质求解】
1.(1)证明: ,
,
,
,
;
(2)如图2,连接,,,,
,
,
,
,
,
,
,
,
,
经过圆心.
∴,,三点共线
2.B
【分析】本题主要考查圆与内接四边形的综合,掌握内接四边形的性质,直径所对圆周角是直角的知识是解题的关键.
根据均是上的点,可得四边形是内接四边形,则,由此可求出的度数,根据是的直径,可得,由此即可求解.
【详解】解:均是上的点,
∴四边形是内接四边形,
∴,
∵,
∴,
∴,
∵是的直径,
∴,
∴,
故选:B.
3.110
【分析】本题考查了圆内接四边形的性质定理,轴对称的性质,熟练掌握圆内接四边形的性质定理及轴对称的性质是解题的关键.根据圆内接四边形的性质定理可得,再根据轴对称的性质即得答案.
【详解】四边形是圆内接四边形,,
,
点D关于的对称点E在边上,
,
.
故答案为:110.
4.(1)证明:,,
,
平分,
平分,
,
四边形是圆内接四边形,
,
,
,
,
;
(2)解:,,
,
,
,
是圆的直径,
垂直平分,
,
,
是等边三角形,
,
,
,
,
,
四边形是圆内接四边形,
,
,
,
,
,,
,
是圆的直径,
圆的半径长是4,
.
【题型5 切线的判定】
1.(1)解:根据题意,作图如下:
则点、为所求.
(2)证明:连接.
是的直径,
,
平分,
,
,
,
,
.
,
,
,
,
,
.
,,
,
,
,
.
又为半径,
是切线.
2.解:与相切.
证明:连接.
∵,
∴.
∵图形沿过点A的直线翻折,点C的对应点落在边上,
∴.
∴.
∴.
∴由,得,即.
∴与相切.
3.(1)解:是的切线,理由如下,
连接,
是圆的直径,
,
,
,
,
,
,
,
半径,
是的切线;
(2)解:连接,
,
,
等边三角形,
,
为的中点,
,
.
故答案为:30.
4.(1)∵是的直径,
∴,
∵,,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解: 存在,,理由如下:
在上取一点,使得,连接,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∵是的直径,
∴,
∵,,
∴,
∴,
∴,
∴.
【题型6 切线的性质】
1.(1)证明:是等边三角形,
.
连接,
∵
则.
是的切线,
.
.
.
.
(2)解:为四边形的外接圆,.
是的中点,
∴
.
∴为直角三角形.
.
.
的面积为.
2.(1)解:连接,
为的直径,,
,
是等边三角形,
,
;
(2)解:连接,与相交于,
是的切线,
,
,
,
,
,
为的直径,
,
,
,
,
.
3.(1)证明:如图,连接.
为圆O的切线,
.
平分,
.
,
,
,,
.
在和中,
,
,
.
是的切线.
(2)解:,
,
,
.
.
是直径,
,
,
.
在中,,,
.
.
4.(1)证明: ,,
,
是的直径,
,
,
,
,
,即,
是半径,
是的切线;
(2)解: ,
,
,
,
是等边三角形,
,
,
,
,
,
,
,
.
【题型7 切线长定理】
1.(1)解:如下图,连接,
与相切于点E,
,
,
,
,
是的半径,,
与相切于点C,
,
在和中,,
,
,
,
;
(2),
,
,
,
,且,
,
解得:,
,
,
点O、点A都在线段的垂直平分线上,
垂直平分,
,
,
,
,
线段,的长分别是1、.
2.A
【分析】此题主要考查了切线的性质和等腰三角形的性质,利用切线的性质得出,进而得出,即可得出,同理:即可得出结论.
【详解】连接,,
,是的切线,
,
∵,
,
,
,
,
,
,
,
同理可得:,
故选:A.
3.
【分析】本题主要考查的知识点是:圆心角、假、张的关系,切线的性质,切线长定理以及解直角三角形的应用等知识,连接,由于C是半圆的三等分点,那么,进而可由切线长定理求得;在中根据半径的长以及的度数,可求得的值,进而可由勾股定求得的长.
【详解】解:连接,
∵C为半圆弧的三等分点,
∴,
∵,都是的切线,
∴,
在中,,则,
在中,由勾股定理得:,
故答案为:
4.(1)证明:∵,
即垂直平分,
∴,
∵,
∴平分,
∴,
∵,
∴为的切线,
∵与半相切,
∴平分,
∴,
即将三等分;
(2)如图2
∵是的直径,
∴
∵,.
∴,
设的半径为,
在中,,
∴,
∵,
∴,
∴,
在中,,
∴,
在中,,
∴是直角三角形且,
∴,
∴点、、、是的四等分点.
【题型8 三角形的外接圆与内切圆】
1.(1)解:连接,
∵是圆O直径,圆O周长为,
∴,,
∴,
∵
∴,
∵是圆O直径,弦,
∴,垂直平分,
∴,
∴是等边三角形,
∴,点O是的内心,
∴,
∴
∴内切圆的面积为;
(2)如图,连接,
∵是等边三角形, ,
∴,,
∴,
∵点O是的内心,
∴,
∴
∴.
2.(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
3.(1)证明:∵I是△ABC的内心,
∴AE平分∠CAB,BI平分∠ABC,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠BIE=∠BAE+∠ABI,∠IBE=∠IBD+∠EBD,
∵∠CBE=∠CAE,
∴∠BIE=∠EBI,
∴EB=EI;
(2)解:连接EC,过点E作EM⊥AB,EN⊥AC交AC的延长线于N,则EM=EN,
∵∠BAE=∠CAE,
∴=,
∴BE=EC=4.
∵AE=AE,EM=EN,
∴△AEM≌△AEN,
∴AM=AN.
∵BE=EC,EM=EN,
△BME≌△CNE(HL),
∴BM=CN.
设BM为x,则8-x=6+x,解得x=1,即BM=1,
∴AM=7.
又∵BE=4,由勾股定理得,EM==.
∴AE==8,
∵EI=BE=4,
∴AI=AE EI=4.
4.(1)解:∵∠CBD=34°
∴∠CAD=34°
∵点E是△ABC的的内心
∴∠BAC=2∠CAD=68°
∴∠EBC+∠ECB=(180°-68°)÷2=56°
∴∠BEC=180°-56°=124°
(2)∵E是△ABC的内心
∴∠BAD=∠CAD,∠EBA=∠EBC
∵ ∠DEB=∠BAD+∠EBA,∠DBE=∠EBC+∠CBD,∠CBD=∠CAD
∴∠DEB=∠DBE
∴DE=DB .
【题型9 正多边形和圆的有关计算】
1.(1)证明:在圆内接正六边形中,
,
∴,
∴.
在和中,
,
∴.
∴.
∴是等边三角形,
∴.
∴点H,G三等分.
(2)①解:如图,即为所求作.
②证明:如图,过点O作,垂足为P,连接,则.
由(1)知,,
∴.
∵,,
∴.
∴是①所作圆的切线.
2.D
【分析】本题主要考查了正多边形和圆,圆内接四边形的性质,熟记圆内接四边形的对角互补是解决问题的关键.
先由正多边形内角和定理求出,再根据圆内接四边形的性质即可求出.
【详解】解:正五边形内接于,
,
四边形是内接四边形,
,
,
故选:D.
3. 4
【分析】本题考查了正多边形与圆,掌握圆的相关性质及正方形的相关性质、准确的辅助线及计算是本题的解题关键.
(1)利用圆的面积公式计算出半径即可求出直径;
(2)连接,,以、为边作,连接,证明出,,当、、共线时,最小,即为的最小值,利用勾股定理求出即可解答此问.
【详解】解:(1)的面积为,
,
的直径长为,
故答案为:;
(2)如图,连接,,以、为边作,连接,
四边形为正方形,
,,
四边为平行四边形,
,
,
,
当、、共线时,最小,即为的最小值,
在中,,,
,
,
,
周长的最小值为,
故答案为:4.
4.(1)解:如图,连接,,与交于点,
由题意可知,,,
∵多边形是正八边形,
∴,
∴,
∴,
∴;
(2)∵所对的圆心角为,
∴所对的圆周角为,
∵,
∴.
【题型10 正多边形中的规律探究性问题】
1. ,
【分析】根据正多边形内角和定理结合全等三角形的判定和性质可得出(1)、(2)、(3)的结论,根据以上规律可得出正n边形的结论.
【详解】(1)∵正三角形ABC中,点M、N是AB、AC边上的点,且AM=BN,
∴AB=AC,∠CAM=∠ABN=,
∵在△ABN和△CAM中,
,
∴△ABN≌△CAM(SAS),
∴AN= CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA =∠OAC+∠BAN =∠BAC=60°,
故结论为:AN= CM,∠NOC=60;
(2)∵正方形ABCD中,点M、N是AB、BC边上的点,且AM=BN,
∴AB=AD,∠DAM=∠ABN=,
同理可证:Rt△ABNRt△DAM,
∴AN= DM,∠BAN=∠ADM,
∠NOD=∠OAD+∠ADM =∠OAD+∠BAN =∠BAC=90°,
故结论为:AN= DM,∠NOD=90;
(3)∵正五边形ABCDE中,点M、N是AB、BC边上的点,且AM=BN,
∴AB=AE,∠EAM=∠ABN=,
同理可证得:Rt△ABNRt△EAM,
∴AN= EM,∠BAN=∠AEM,
∠NOE=∠OAE+∠AEM =∠OAE+∠BAN =∠BAE=108°,
故结论为:AN= EM,∠NOE=108;
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
∴以上所求的角恰好等于正n边形的内角,
在正n边形中,点M,N是上的点,且,与相交于O,结论为: ,.
故答案为: ,.
2.D
【详解】解:连结OE1,OD1,OD2,如图,根据正六边形的性质得∠E1OD1=60°,则△E1OD1为等边三角形,再根据切线的性质得OD2⊥E1D1,于是可得OD2=E1D1=×2,利用正六边形的边长等于它的半径得到正六边形A2B2C2D2E2F2的边长=×2,同理可得正六边形A3B3C3D3E3F3的边长=()2×2,依此规律可得正六边形A10B10C10D10E10F10的边长=()9×2=,
故选:D,
3.
【分析】作多边形的半径,根据多边形的性质可证,得,再根据“等边对等角”得,于是可得,从而可证则,因此.
本题考查了正多边形的性质、全等三角形的判定和性质、等边对等角、正多边形中心角等知识点,解题的关键综合运用这些性质解题.
【详解】不失一般性,设时的情形,可以推广到一般情况.连接,如下图
由正多边形的性质知:
∴
∴
由得:
∴
即:
又∵
∴
∴
∴
即:
∵
∴
故答案为:.
4.(1)解:由题意得,,
故答案为:;
(2)解:假设正方形边长1,
∴此时正方形的内切圆半径为,
∴;
设正六边形的边长为1,内切圆圆心为O,则,
又∵,
∴是等边三角形,
∴,
∴,
∴;
(3)解:,随着n的增大,越来越接近于1.由张衡、祖冲之的研究,精进的取值的方法可知:正多边形,边长数越多,越接近于圆,因此当边长增多时,其周长L也与对应的内切圆周长更接近,其比值更接近于1.
【题型11 圆锥侧面展开图的有关计算】
1.(1)解:如图,过A、分别作、的垂线,它们相交于,然后以为半径作,
则即为所求;
(2)解:∵,,
,
由作图知
和分别是切线,
,
,
为等边三角形,
则长为:,
所在的扇形围成圆锥的侧面,则该圆锥的底面圆的半径设为r,
,
,
则该圆锥的底面圆的半径设为;
(3)∵,,
,
由作图知
和分别是切线,
,
,
为等边三角形,
,,
∵,
垂直平分,
平分,
,
,
劣弧与线段、围成的封闭图形的面积
.
2.(1)解:连接,
∵,
∴是圆O的直径,
∴点A、O、B三点共线,
∴,
又∵,
∴,
∵圆的直径为2,
则,
故.
∴;
(2)解:的长,
则,
解得:.
故该圆锥的底面圆的半径是.
3.(1)解:设该圆锥的底面半径为r,
由题意得.
解得,
即该圆锥的底面半径为1.
(2)存在,的长为定值.如图,连接.
∵,,
∴D为中点,E为中点.
∴为的中位线.
∴.
∵,,
∴.
∴.
4.(1),,
,
,
扇形纸板的圆心角度数为;
(2)如图所示.连接,过点P作,线段就是彩带长度的最小值,
由(1)得,
彩带长度的最小值为.
【题型12 不规则图形面积的计算】
1.B
【分析】过点作于点,过点作交的延长线于点,设交于点,交于点,根据题意得出,进而根据即可求解.
【详解】解:如图所示,过点作于点,过点作交的延长线于点,设交于点,交于点,
∵
则四边形是正方形,
,
∴,
,
,
,
在中,,
,
,
,
∴,
,
,
,
,
故选:B.
【点睛】本题考查了求扇形面积,旋转的性质,正方形的性质,掌握扇形面积公式是解题的关键.
2.
【分析】本题考查正方形的判定和性质,全等三角形的判定和性质,扇形的面积,作辅助线构造全等三角形是解问题的关键.
连接,过点D作于点M,过点D作于点N,先证明是正方形,然后证明,最后运用解题即可.
【详解】如图,连接,过点D作于点M,过点D作于点N,
则
∵,
∴,,四边形是矩形
∵,D是的中点,
∴
∴
同理
∴四边形是正方形
∴,
由题可知,,
∴
在与中,
,
∴
∴
∵
∴
故答案为
3.C
【分析】连接,根据切线长定理和切线的性质可知四边形是正方形,从而证明,由等腰直角三角形的性质推出,从而证明,利用平行线间距离相等从而得到,继而得到阴影部分的面积等于扇形的面积,从而利用得到扇形半径的长度,从而得到的长,继而得出的长.
【详解】解:连接,
∵半圆O与相切于点D、E,
∴,.
∵,
∴四边形是矩形,
又∵,
∴四边形是正方形.
∴,.
又∵,,点O是边的中点,
∴,,
∴.
∵,,
∴.
∵平行线间距离相等,
∴,
∴阴影部分的面积等于扇形的面积.
∵阴影部分的面积为,
∴,
∴,
∴,
∴.
故选:C.
4.(1)解:弦于,是的直径,
,
,
故答案为:30;
(2)解:与相切,
理由如下:
连接,如图所示:
弦于,是的直径,
,,
,
,
,
,
,
,
是的半径,
与相切;
(3)解:是的直径,
,
,,
,
,
连接,如图所示:
点是的中点,
,
,
是的中位线,
,,
,
,
,
图中阴影部分的面积的面积扇形的面积的面积.
【题型13 利用弧长和扇形面积公式解决几何图形的旋转问题】
1.(1)解:把绕着点逆时针旋转得到,则是等边三角形,
,
是等边三角形,
,
,
,
在和中,
,
,,
在中,,,,则,由勾股定理的逆定理可知为直角三角形,且,
;
(2)解:把绕着点逆时针旋转得到,则是等边三角形,
;
(3)解:如图所示:
把绕着点逆时针旋转得到,点划过的路径是,则长度为;
(4)解:由(1)的证明过程可知,,点划过的路径是,点划过的路径是,如图所示:
由旋转性质可知,
扫过的区域的面积
.
2.B
【分析】正方形 在直线上顺时针连续翻转4次,实际点经过的路径有三段,其中一段以为半径,圆心角为的弧长,另两段是以为半径,圆心角为的弧长,然后根据弧长公式计算.
【详解】解:点经过的路径如图
因为正方形 的边长为,
所以,
所以点所经过的路径长.
故选:B.
3.B
【分析】本题考查了旋转的性质、弧长的计算、轨迹等知识,由在矩形中,已知,可求得的长,由旋转的性质,易得,又由,即可求得的度数,继而求得答案.
【详解】解:连接,
∵在矩形中,,
,
,
根据旋转的性质可知:,
根据矩形的性质可知:,
,
,
,
∴点的运动路径长为: .
故选B.
4.解:(1)如图所示,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段弧,即弧OO1、弧O1O2以及弧O2O3,
∴ 顶点O运动过程中经过的路程为:
,
顶点O在此运动过程中所形成的图形与直线l2围成图形的面积为:
=1+π,
正方形OABC经过5次旋转,顶点O经过的路程为:
.
(2)∵ 正方形OABC经过3次旋转,顶点O经过的路程为:
,
根据第四次正方形旋转O点不动,也就是此时也是正方形OABC经过4次旋转的路程,
∴ π=10×π+π,
∴正方形纸片OABC经过了:10×4+1=41次旋转.
