北师大版九年级数学下册 第三章 圆--切线长定理与三角形的内切圆 复习题 (含解析)
文档属性
| 名称 | 北师大版九年级数学下册 第三章 圆--切线长定理与三角形的内切圆 复习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 16:44:56 | ||
图片预览

文档简介
第三章《圆》复习题-- 切线长定理与三角形的内切圆
【题型1 利用切线长定理求线段长度】
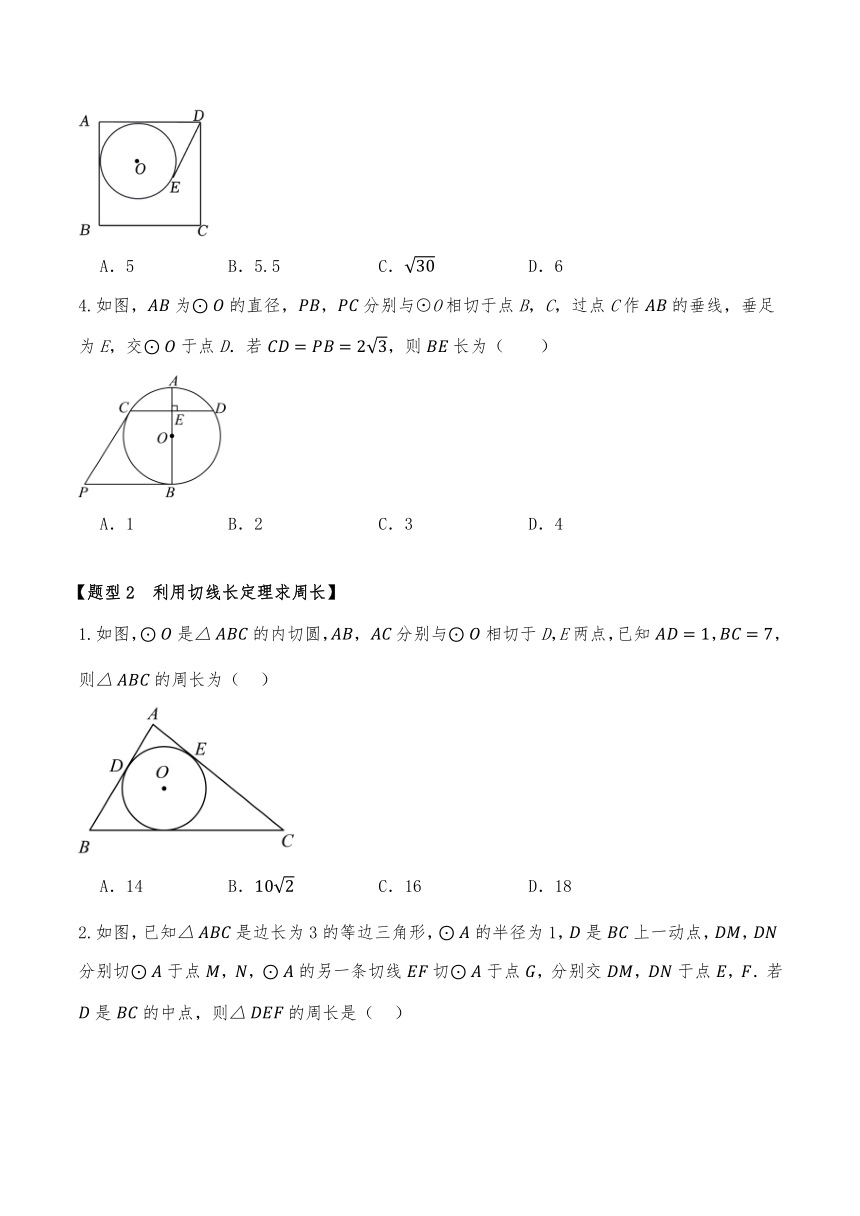
1.如图,等腰的内切圆与,,分别相切于点D,E、F,且,,则的长是( )
A. B. C. D.
2.如图,是的切线,为切点,经过圆心,若,则的长度是( )
A. B. C. D.
3.如图,与正方形的两边,相切,且与相切于E点.若的半径为4,且,则的长度为( )
A.5 B.5.5 C. D.6
4.如图,为的直径,,分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
【题型2 利用切线长定理求周长】
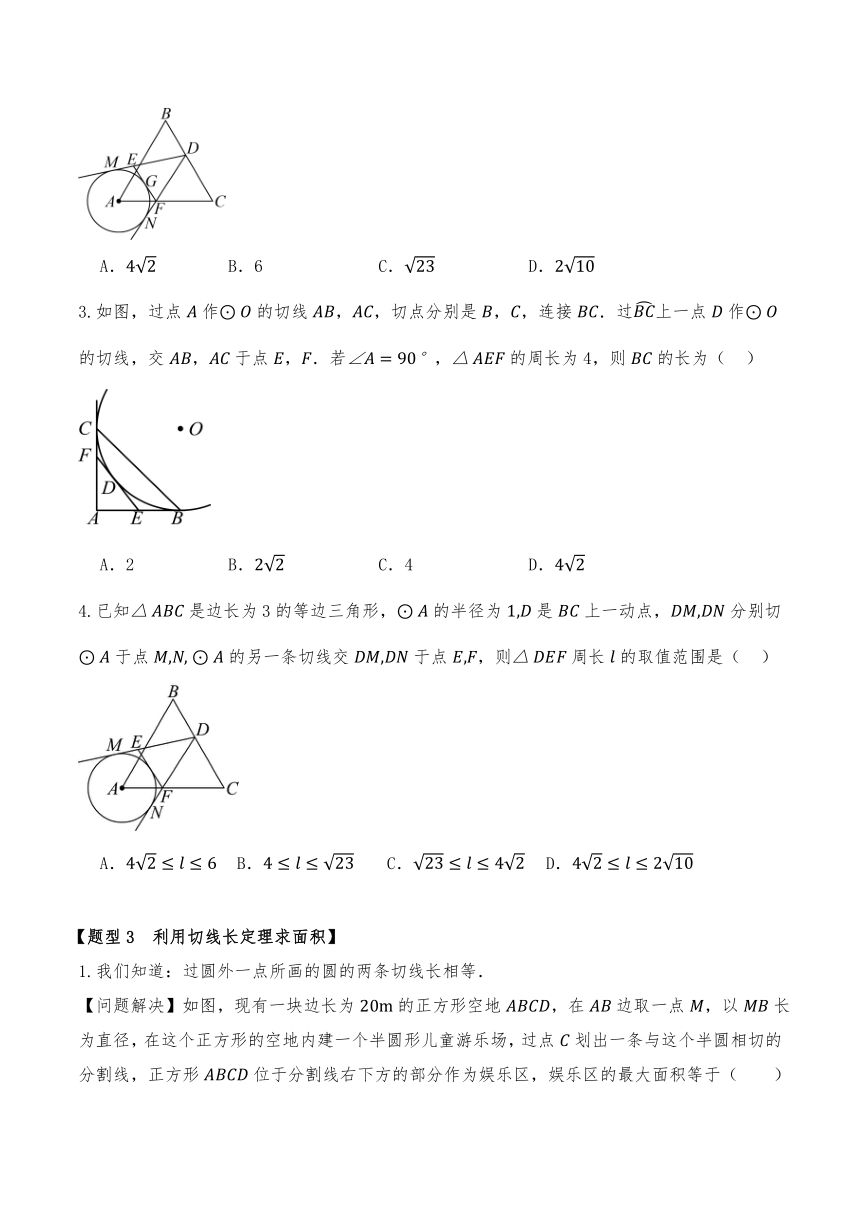
1.如图,是的内切圆,分别与相切于D,E两点,已知,,则的周长为( )
A.14 B. C.16 D.18
2.如图,已知是边长为3的等边三角形,的半径为1,是上一动点,,分别切于点,,的另一条切线切于点,分别交,于点,.若是的中点,则的周长是( )
A. B.6 C. D.
3.如图,过点作的切线,,切点分别是,,连接.过上一点作的切线,交,于点,.若,的周长为4,则的长为( )
A.2 B. C.4 D.
4.已知是边长为3的等边三角形,的半径为是上一动点,分别切于点的另一条切线交于点,则周长的取值范围是( )
A. B. C. D.
【题型3 利用切线长定理求面积】
1.我们知道:过圆外一点所画的圆的两条切线长相等.
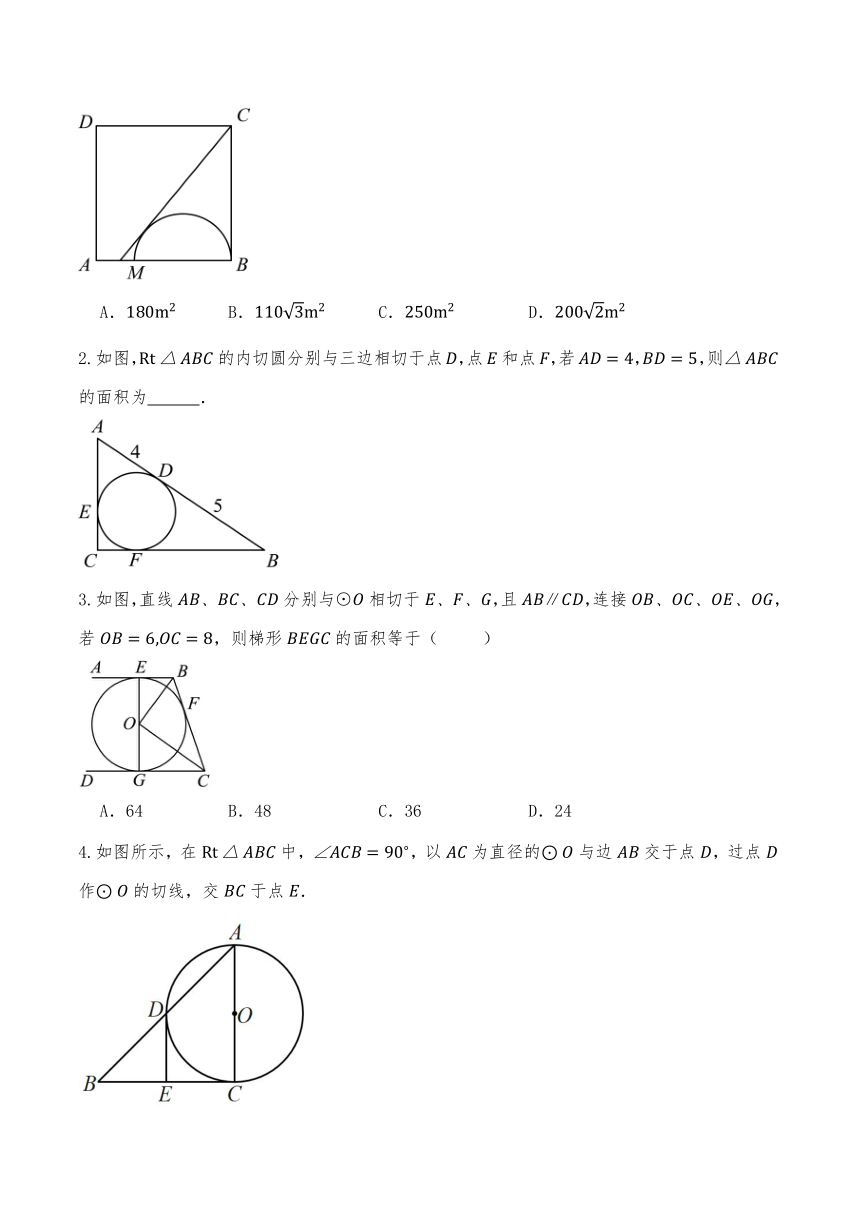
【问题解决】如图,现有一块边长为的正方形空地,在边取一点,以长为直径,在这个正方形的空地内建一个半圆形儿童游乐场,过点划出一条与这个半圆相切的分割线,正方形位于分割线右下方的部分作为娱乐区,娱乐区的最大面积等于( )
A. B. C. D.
2.如图,的内切圆分别与三边相切于点,点和点,若,,则的面积为 .
3.如图,直线分别与⊙相切于,且∥,连接,若,则梯形的面积等于( )
A.64 B.48 C.36 D.24
4.如图所示,在中,,以为直径的与边交于点,过点作的切线,交于点.
(1)求证:.
(2)若以,,,四点为顶点的四边形是正方形,的半径为,求的面积.
(3)若,,求的半径的长.
【题型4 利用切线长定理求角度】
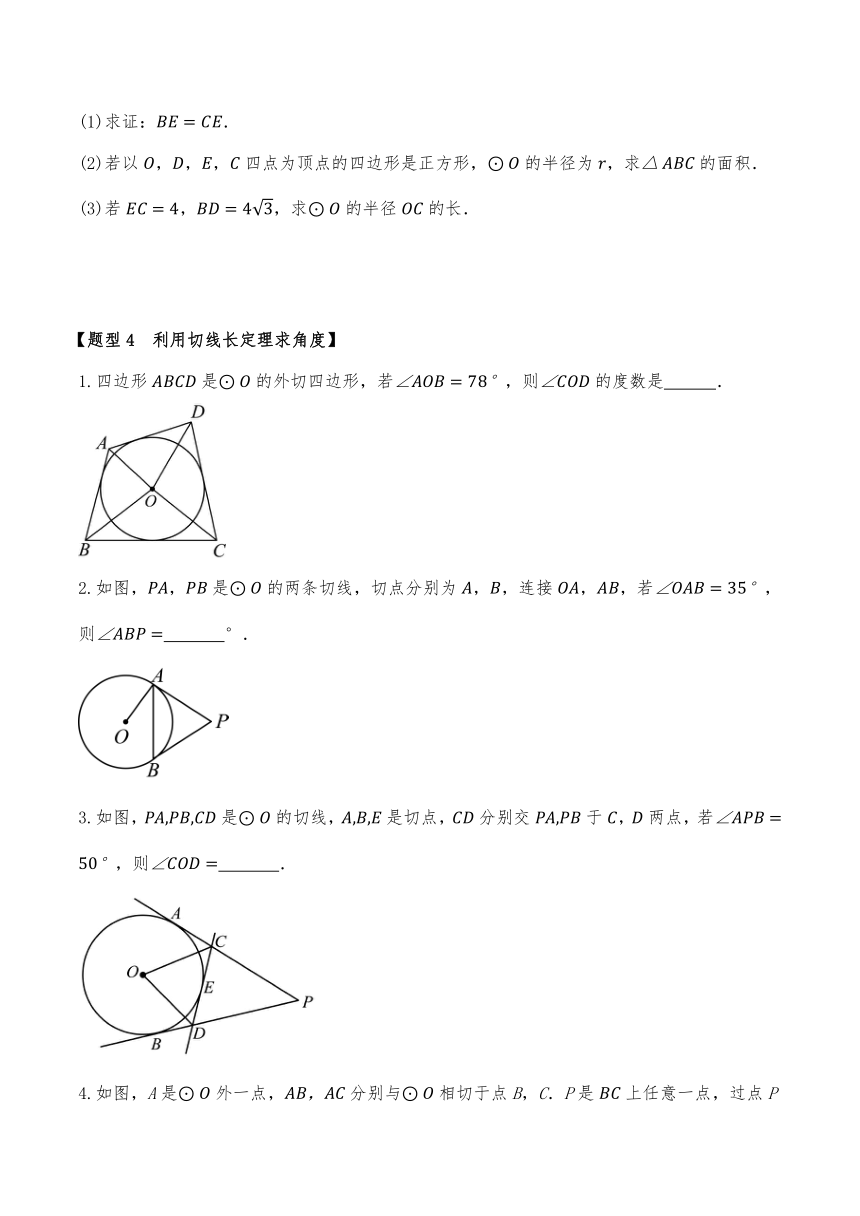
1.四边形是的外切四边形,若,则的度数是 .
2.如图,,是的两条切线,切点分别为,,连接,,若,则 °.
3.如图,是的切线,是切点,分别交于,两点,若,则 .
4.如图,A是外一点,分别与相切于点B,C.P是上任意一点,过点P作的切线,交于点M,交于点N.,则的周长是 ,若,则 .
【题型5 利用切线长定理进行证明】
1.如图,是的直径,,是的两条切线,切点分别为B,C.连接交于点D,交于点E,连接.
(1)求证:;
(2)若点E是的中点,的半径为6,求的长.
2.如图,,是的切线,,为切点,连接.
(1)若与相切于点,求证;
(2)若,求证与相切.
3.如图,在中,为直径,点M为延长线上的一点,与相切于点C,圆周上有另一点D与点C分居直径两侧,且使得,连接.
求证:①与相切;
②四边形是__________形;
③__________.
4.如图1所示,为的外接圆,为直径,、分别与相切于点D、C().E在线段上,连接并延长与直线相交于点P,B为中点.
(1)证明:是的切线.
(2)如图2,连接,,求证:.
【题型6 利用切线长定理求内切圆半径】
1.如图,在中,,,,则的内切圆半径 .
2.如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是,量角器与刻度尺接触点在刻度尺上的读数是,量角器与三角板的接触点为B.
(1) .
(2)该量角器的直径长为 .(结果保留根号)
3.如图,在四边形中,分别与相切于B、E、A三点,为的直径.若,则的半径为 .
4.如图, 内切于正方形,边、上两点,,且是的切线,当的面积为时,则的半径是 .
【题型7 作三角形的内切圆】
1.如图,在的正方形网格中,有部分网格线被擦去.点,,在格点(正方形网格的交点)上.
(1)请用无刻度的直尺在图1中找到三角形的外心;
(2)请用无刻度的直尺在图2中找到三角形的内心.
2.为建设绿色花园城市,某小区要在一块等边空地内修建一个圆形花坛.
(1)实践与操作:要使花坛面积最大,用尺规作图法画出圆形花坛示意图(保留作图痕迹,不要求写作法);
(2)应用与计算:在(1)的条件下,米,求圆形花坛的面积.
3.如图,点C,D分别在射线OA、OB上,求作⊙P,使它与OA、OB、CD都相切.(使用直尺、圆规、直角板作图并保留作图痕迹)
4.按着要求画图.
(1)在图1中,利用直尺和圆规,作出的内切圆(不写作法,保留作图痕迹);
(2)如图2,由小正方形构成的网格中,每个正方形的顶点叫做格点.的顶点都在格点上,经过、、三点,仅用无刻度的直尺在给定的网格中按要求作图(不写作法,保留作图痕迹).
①在图2中,找出的圆心.
②在图2中的边上找到一点,使得平分;
③在图2备用图中的上找到一点(不与点重合),使得.
【题型8 三角形内切圆中求最值】
1.如图,矩形的顶点A,C分别在x轴、y轴上,点B的坐标为,是的内切圆,点N,点P分别是,x轴上的动点,则的最小值是 .
2.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
3.如图,点B的坐标为,以O点为圆心,以为半径的圆交y轴于点A,点C为第一象限圆上一动点,轴于D点,点I为的内心,则的最小值为 .
4.如图,以的斜边为直径作,为的内心,点为上一个动点,为的中点,若,,则的最大值为 .
【题型9 三角形周长、面积与内切圆半径的关系】
1.如图,已知中,,为的内切圆,若,且的面积为24,则的周长为( )
A.48 B. C.24 D.
2.如图,是的内切圆,若的周长为18,面积为9,则的半径是( )
A.1 B. C.1.5 D.2
3.如图,在中,,为中线,若,,设与的内切圆半径分别为,,则的值为( )
A. B. C. D.
4.小明准备以“青山看日出”为元素为永嘉县某名宿设计标志示意图,如图所示,他利用两个等边三角形和一个圆分别表示青山和日出,已知点,,,在同一条直线上,且,四边形和四边形的面积之差为,则的长是 ;连结,若是的内切圆,则圆心到的距离是 .
【题型10 三角形的内切圆与外接圆的综合】
1.如图,中,,,内心为I,连接并延长交的外接圆于D,若,则 ( )
A. B.1 C. D.
2.一个三角形三边长分别为5,12,13,R是其外接圆半径,r是其内切圆半径,则R﹣r= .
3.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
4.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长.
参考答案
【题型1 利用切线长定理求线段长度】
1.D
【分析】连接,,,,,,交于点M,根据“从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角”可得,,,结合求得点E是中点,然后由等腰三角形三线合一的性质求得点A,O,E共线,在中由勾股定理求得后,利用的面积求得内切圆的半径;由切线长定理和等腰三角形三线合一的性质可得垂直平分,在中由勾股定理求得后,再利用面积法求得即可解答;
【详解】解:如下图,连接,,,,,,交于点M,
由切线长定理可知平分,,
∵,
∴,
∴,
同理根据切线长定理可知平分,,,
∴,
∴点E是中点,
根据等腰三角形三线合一的性质可得点E在的延长线上,即点A,O,E共线,
∴,
中由勾股定理可得,
∵且,
∴,
中由勾股定理可得,
等腰中由三线合一的性质可得垂直平分,
∵,
∴,
∴,
故选: D.
2.B
【分析】本题考查了切线的性质定理,切线长定理,勾股定理,根据切线长定理,得到,根据切线性质,得,勾股定理计算即可.
【详解】∵是的切线,为切点,经过圆心,,
∴,,,
∴,
故选:B.
3.D
【知识点】根据正方形的性质与判定求线段长、切线的性质定理、应用切线长定理求解
【分析】设与正方形的边,切于点F,H,先证四边形是正方形,求出,再根据切线长定理可得.
【详解】解:如图,设与正方形的边,切于点F,H,
则,
,,
四边形是正方形,
的半径为4,且,
,,
,
与相切于点E,
,
故选D.
4.C
【知识点】用勾股定理解三角形、根据矩形的性质与判定求线段长、利用垂径定理求值、应用切线长定理求解
【分析】作于H,由垂径定理得到的长,从而求出的长,由勾股定理求出的长,即可求出的长.
【详解】解:作于H,
∵直径于H,
∴,
∵,分别切于C,B,
∴,直径,
∴四边形是矩形,
∴,,
∴,
∴,
∴.
故选:C.
【题型2 利用切线长定理求周长】
1.C
【分析】本题主要考查切线长定理,熟练掌握切线长定理是解题的关键.
根据切线长定理得到,根据即可得到的周长.
【详解】解:如图:∵的内切圆分别与相切于点,且,
∴,
∵,
∴,
∴的周长,
故选:C.
2.C
【知识点】等边三角形的性质、切线的性质定理、应用切线长定理求解
【分析】本题主要考查了切线的性质和切线长定理,根据切线长定理可知的周长,连接在中,由勾股定理求出的长即可得出结论
【详解】解:连接,如图,
∵是等边三角形,
∴
∵是的中点,
∴,
∵分别切于点M,N,
∴,
同理:,
∴的周长,
在中,,
∴的周长为,
故选:C
3.B
【分析】本题考查切线长定理,勾股定理;利用切线长定理得出,,,再根据三角形周长等于4,可求得,从而利用勾股定理可求解.
【详解】解:∵,是的切线,切点分别是,,
∴,
∵、是的切线,切点是D,交,于点,,
∴,,
∵的周长为4,即,
∴,
∵,
∴,
故选:B.
4.C
【知识点】等边三角形的性质、用勾股定理解三角形、切线的性质定理、应用切线长定理求解
【分析】连接,,根据切线长定理和切线性质、勾股定理求得,根据垂线段最短可得,当时,最小,求出最小值为,当点D与点B(或C)重合时,AD最长,此时,即可得出,从而可求得l最大与是最小值,即可得出答案.
【详解】解:连接,,设切于G,
∵,分别是的切线,
∴,
∵是的切线,
∴,,
∴,
∴周长,
∵是的切线,
∴,
∴,
∴,
∴当最小时,l最小,当最大时,l最大;
根据垂线段最短可得,当时,最小,
∵是边长为3的等边三角形,,
∴,
由勾股定理得:,
当点D与点B(或C)重合时,AD最长,此时,
∴,
∴.
故选:C.
【题型3 利用切线长定理求面积】
1.C
【分析】本题考查切线的性质,正方形的性质,勾股定理,关键是掌握切线长定理.
当半圆面积最大,即M与A重合时,娱乐区的面积最大,由切线长定理得到,,由勾股定理列出关于的方程,求出的长即可解决问题.
【详解】解:当半圆面积最大,即M与A重合时,娱乐区的面积最大,与半圆相切于H,交于P,
∵四边形是正方形,
∴,
∴分别是半圆的切线,
∴,
设,则,,,
在中,,
∴,
∴,
∴,
∴娱乐区的最大面积梯形的面积.
故选:C.
2.20
【分析】直接利用切线长定理得出,,,设,再结合勾股定理得出的长,进而得出答案.
本题考查了切线长定理和勾股定理,解决本题的关键是正确理解题意,熟练掌握切线长定理的相关内容,找到线段之间的关系.
【详解】的内切圆分别与斜边、直角边、切于点D、E、F,,,
,,,
设,
则
整理得,,
解得:,(不合题意舍去),
则, ,
,
故的面积为20,
故答案为20.
3.B
【知识点】应用切线长定理求解
【分析】先根据切线长定理得出,然后利用面积求出OF的长度,即可得到圆的半径,最后利用梯形的面积公式 即可求出梯形的面积.
【详解】连接OF,
∵直线分别与⊙相切于,
∴ .
在 和 中,
∴,
∴.
在 和 中,
∴,
∴.
∵ ,
.
∵,
.
,
∴ ,
,
∴梯形的面积为
.
故选:B.
4.(1)证明:如图所示,连接.
∵是直径,
∴
∴
,都是的切线,
,
;
又,,
,
.
.
(2)如图,连接.
当以,,,四点为顶点的四边形是正方形时,,
∴;
∵
∴,
∴
∵
.
(3)若,则
∵
∴
∴,即
∵ ,
∴,
在中,,
∴,
∴
【题型4 利用切线长定理求角度】
1.
【分析】本题主要考查了切线长定理,解题的关键是熟练掌握切线长定理及其推论.令四边形与分别相切于点E、F、G、H,连接,通过证明,即可求解.
【详解】解:令四边形与分别相切于点E、F、G、H,
连接,
∵是的外切四边形,
∴,
∵,
∴,
∴,
同理可得:,
∵,
∴,
∴,
∴,
故答案为:.
2.
【分析】本题考查了切线的性质以及切线长定理.根据题意可得,,进而求得,根据等边对等角,即可求解.
【详解】解:,是的两条切线,
,,
,
,
,
.
故答案为:.
3.
【分析】本题考查了切线的性质定理以及切线长定理,连接,由切线的性质可求出,再由切线长定理可得出,可求得答案.
【详解】解:如图,连接,
∵分别为的切线,
∴,
∴,
∵为的切线,
∴,
∴,
故答案为:.
4.
【分析】本题考查切线的性质、切线长定理,圆周角定理,先利用勾股定理可计算出的长,再根据切线长定理得到得到的周长,由四边形的内角和得到的度数,然后利用圆周角定理计算是解题的关键.
【详解】解:连接,,,
∵分别与切于点B,C,
∴,,,
在中,,
∵与相切于P,
∴,
∴的周长.
∵,,
∴,
∴,
∴优弧的度数为,
∴,
故答案为:,.
【题型5 利用切线长定理进行证明】
1.(1)证明:∵,是的两条切线,切点分别为,,
∴,,
∴,,
∵,
∴是的中位线,
∴;
(2)∵,点是的中点,
∴,
∴为等边三角形,
∴,
∴,
∵是的切线,
∴,
∵的半径为6,
∴,
∴,
∴.
2.(1)证明:∵与相切,切点为,且,是的切线,,为切点,
∴ ,,
∵,
∴;
(2)证明:延长到点,使得,连接,过点作,垂足为G,连接,,,,
∵,,
∴ ,
∵,是的切线,,为切点,
∴,,
∵,,,
∴,
∴,
又∵,,
∴,
∴,
∴平分,
又∵,,
∴,
∴与相切.
3.
解:①证:连接OC,OD
在和中
,
,
,
是的切线,
,
∴与相切;
②由①可知:,
又∵CM=DM,AM=AM,
∴,
∴AC=AD,
∵AC=AD=CM=MD,
∴四边形是菱形;
故答案为:菱;
③∵AM=CM,OC=OD,
∴,,
∵,
∴,
∵与相切,
∴,
∴,
又∵是菱形,
∴ ,
∴,
故答案为:.
4.(1)证明:连接,
∵为直径,
∴.
在中,B为中点,
∴,
∴,
∵,
∴,
又∵为切线,
∴,
∴
∴.
即,
∴是的切线.
(2)证明:∵、、分别与相切于点D、E、C,
∴,,,,
∴,
∴,
∴,
∴,
∴;
【题型6 利用切线长定理求内切圆半径】
1.1
【分析】本题考查了切线长定理,圆的切线的性质,正方形的判定与性质,熟练掌握切线长定理是解答本题的关键,首先利用切线的性质证明四边形是正方形,得到,再利用切线长定理得到,,最后由列方程即可求解.
【详解】设的内切圆与、、分别相切于点D、E、F,
,,
,
四边形是矩形,
,
四边形是正方形,
,
,,
,,
,,
在中,,
,
,
解得 .
故答案为:1.
2. 2
【分析】本题考查了切线长定理,含30度角直角三角形的特征,勾股定理.根据题意得出和与量角器相切,则,,进而得出,即可解答.
【详解】解:令量角器与刻度尺接触点为点C,量角器圆心为点O,
根据题意可知,和与量角器相切,
∴,,,
∵A在刻度尺上的读数是,C在刻度尺上的读数是,
∴,
∵,
∴,
∵,
∴,
∴,
根据勾股定理可得:,
∴该量角器的直径长为,
故答案为:2,.
3.
【分析】本题考查了切线的性质,切线长定理,勾股定理,矩形的判定与性质,根据切线的性质把图形分割为矩形和直角三角形是解题的关键.
过D作于F,由切线的性质得四边形是矩形,则;由切线长定理可得的长,由勾股定理即可求解.
【详解】解:如图,过D作于F,
∵与,
∴,
∴,
∴四边形是矩形,
∴,
∴;
∵分别与相切,
∴,
∴;
在中,由勾股定理得:,
∴,
∴的半径为.
故答案 为:
4.
【分析】设正方形的边长为,则,设,,则,,,利用勾股定理得出,再由,得出,从而求出,得到.
【详解】解:设与相切于,与相切于,与相切于,
设正方形的边长为,
,
设,,
在中,
,,,
,
,
,
,
,
,
的半径为,
故答案为:.
【题型7 作三角形的内切圆】
1.解:(1)如图,点即为所求;
(2)如图,点即为所求.
2.(1)解:所作图形如图所示:
(2)解:∵是等边三角形,
∴米,,
∵平分,
∴米,
∴米,
由作图可知点O为的内切圆的圆心,也是的重心,
∴米,
∴圆形花坛的面积为.
3.解:如图,作∠DOC的平分线OM,∠ODC的平分线DN,OM交DN于点P1,作P1F⊥OD,以P1为圆心,P1F为半径作⊙P1即可;同法作出⊙P2.
,即为所求;
4.(1)解:如图,即为的内切圆;
(2)解:①圆心如下图所示;
②点如下图所示;
③点如下图所示.
【题型8 三角形内切圆中求最值】
1.4
【分析】延长到点,使,则点与点关于轴对称,则,过点作轴于点,连接交轴于点,交于点,则,当,,,在一条直线上时,取得最小值;利用点的坐标的特征求得线段,,利用三角形的面积关系求得的半径,延长交于点,利用矩形的性质和勾股定理求得的长度,则结论可得.
【详解】解:如图,延长到点,使,则点与点关于轴对称,则,过点作轴于点,连接交轴于点,交于点,则,当,,,在一条直线上时,取得最小值,
点的坐标为,
点的坐标为,
,,
设与三边的切点为,,,连接,,,则,,,设,
,
,
,
,
,
延长交于点,
,,
,,
,,
,
,
的最小值为4.
故答案为:4.
2.
【分析】由矩形的性质得出,,由勾股定理得出,设△的内切圆的半径为,则,解得,连接,易证是的中位线,得出,当经过圆心时,最长,则此时最长,作于,于,则,,由勾股定理得出,则,即可得出结果.
【详解】解:四边形是矩形,
,,
,
设△的内切圆的半径为,
则,
解得:,
连接,
是边上的中点,点是的中点,
是的中位线,
,
当经过圆心时,最长,则此时最长,
作于,于,
则,,
,
,
;
故答案为:.
3.
【分析】连接,作的外接圆,圆心为P,根据内心定义证明,可得,当A,I,P三点共线时,取得最小值,此时,然后根据勾股定理即可解决问题.
【详解】解:如图,连接,作的外接圆,圆心为P,连接,,
∵点I为的内心,
∴,
在和中,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵点B的坐标为,
∴,
∴,
∴P,
当A,I,P三点共线时,取得最小值,
此时
.
故答案为:.
4.
【分析】此题考查了三角形的内切圆和外接圆,连接,,,取中点,连接,过作于点,则点在以点为圆心,为半径的圆上运动,当点三点共线时,最大值为,然后由勾股定理求出的值即可,解题的关键是熟练掌握切线长定理,三角形中位线性质定理和勾股定理的应用.
【详解】解:如图,连接,,,取中点,连接,过作于点,
∵,,,
∴由勾股定理得:,
∵为的中点,
∴,
则点在以点为圆心,为半径的圆上运动,
当点三点共线时,最大,为的值,
∵为的内心,过作于点,于点,
∴四边形为正方形,
由直角三角形的内切圆半径为,即,
∴,
取的中点G,连接,
∴,,
∵,
∴,
∴,
∴,
在中,由勾股定理得:
,
∴最大值为,
故答案为:.
【题型9 三角形周长、面积与内切圆半径的关系】
1.C
【分析】本题考查了三角形内切圆的性质及正方形的判定和性质.
设的半径为r,与的三边、、的切点分别为D、E、F,连接、、.先证四边形是正方形,则,根据勾股定理求出r.又由 的周长内切圆半径,即可求出的周长.
熟练掌握“三角形内切圆的圆心是三条角平分线的交点,它到三角形三条边的距离相等”这一性质,并且能求出内切圆的半径是解题的关键.
【详解】解:如图,设的半径为,与的三边、、的切点分别为,连接、、,则,,,且,
又,
∴四边形是正方形,
,
,
,
解得,
,
,
,即的周长为,
故选:C.
2.A
【分析】作辅助线如解析图,根据,代入数据求解即可.
【详解】解:如图,设与的各边分别相切于点E、F、G,连接,设的半径为r,
则,,
∵
,
又的周长为18,面积为9,
∴,
∴,
故选:A.
3.C
【分析】此题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,三角形的内切圆和面积,设的内切圆为,与 分别相切于点,由,,得,,连接,由可得,即得,同理得,进而即可求解,正确地作出辅助线是解题的关键.
【详解】解:设的内切圆为,与 分别相切于点,
∵,,,
∴,
,
∵为斜边上的中线,
∴,
∴,
连接,,,,,,则,
∵ ,且,,,
∴,
解得,
同理可得,,
解得,
∴,
故选:C.
4.
【分析】设,表示出相关线段的长,根据四边形和四边形的面积之差,得到,求出值即可;连结,连接并延长交于点,设圆与的切点为,连接,连接,作,垂足为,证明为直角三角形,求出内切圆半径,再根据切线长定理得到,从而证明,求出,从而得到即可.
【详解】解: ,
设,则,
,,
与为等边三角形,
,,
,
,
,
,
.
连结,连接并延长交于点,设圆与的切点为,连接,连接,作,垂足为,
等边的边长为,为中点,
,,
,
,
,
,,
,
,
,,
,
,为直角三角形,
内切圆半径,
,
,
,
,,
,
,
,
,
,
圆心到的距离为,
故答案为:,.
【题型10 三角形的内切圆与外接圆的综合】
1.D
【分析】设的外接圆的圆心为O,连接,,,,根据圆周角定理证得是等边三角形,再根据垂径定理可得,,再根据三角形内心证得,进而解决问题.
【详解】解:如图,设的外接圆的圆心为O,连接,,,,
在中,,,内心为I,
∴平分,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,,
∵I是的内心,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故选:D.
2.4.5
【分析】根据勾股定理的逆定理推出,连接,,根据圆是的内切圆,得到,,,,推出正方形,设,得到方程,求出方程的解即可,进而得出其外接圆的半径,即可得出答案
【详解】如图:连接,
,
圆是的内切圆
,,,
四边形是正方形
设
直角三角形斜边长是直角三角形外接圆的直径
其外接圆半径为:
故答案为:
3.(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
4.(1)证明:连接OD.
∵点I是△ABC的内心,
∴∠2=∠7,
∴ = ,
∴OD⊥AC,
又∵∠1=∠ADF,∠2=∠ABC,∠ADF=∠ABC,
∴∠1=∠2,
∵∠3=∠2,
∴∠1=∠3,
∴DGAC;
∴OD⊥DG,
∴DG是⊙O的切线;
(2)解:∵点I是△ABC的内心,
∴∠5=∠6,
∵∠4=∠7+∠5=∠3+∠6,
即∠4=∠DAI,
∴DA=DI;
∵∠3=∠7,∠AED=∠BAD,
∴△DAE∽△DBA,
∴AD:DB=DE:DA,即AD:9=4:AD,
∴AD=6,
∴DI=6.
【题型1 利用切线长定理求线段长度】
1.如图,等腰的内切圆与,,分别相切于点D,E、F,且,,则的长是( )
A. B. C. D.
2.如图,是的切线,为切点,经过圆心,若,则的长度是( )
A. B. C. D.
3.如图,与正方形的两边,相切,且与相切于E点.若的半径为4,且,则的长度为( )
A.5 B.5.5 C. D.6
4.如图,为的直径,,分别与⊙O相切于点B,C,过点C作的垂线,垂足为E,交于点D.若,则长为( )
A.1 B.2 C.3 D.4
【题型2 利用切线长定理求周长】
1.如图,是的内切圆,分别与相切于D,E两点,已知,,则的周长为( )
A.14 B. C.16 D.18
2.如图,已知是边长为3的等边三角形,的半径为1,是上一动点,,分别切于点,,的另一条切线切于点,分别交,于点,.若是的中点,则的周长是( )
A. B.6 C. D.
3.如图,过点作的切线,,切点分别是,,连接.过上一点作的切线,交,于点,.若,的周长为4,则的长为( )
A.2 B. C.4 D.
4.已知是边长为3的等边三角形,的半径为是上一动点,分别切于点的另一条切线交于点,则周长的取值范围是( )
A. B. C. D.
【题型3 利用切线长定理求面积】
1.我们知道:过圆外一点所画的圆的两条切线长相等.
【问题解决】如图,现有一块边长为的正方形空地,在边取一点,以长为直径,在这个正方形的空地内建一个半圆形儿童游乐场,过点划出一条与这个半圆相切的分割线,正方形位于分割线右下方的部分作为娱乐区,娱乐区的最大面积等于( )
A. B. C. D.
2.如图,的内切圆分别与三边相切于点,点和点,若,,则的面积为 .
3.如图,直线分别与⊙相切于,且∥,连接,若,则梯形的面积等于( )
A.64 B.48 C.36 D.24
4.如图所示,在中,,以为直径的与边交于点,过点作的切线,交于点.
(1)求证:.
(2)若以,,,四点为顶点的四边形是正方形,的半径为,求的面积.
(3)若,,求的半径的长.
【题型4 利用切线长定理求角度】
1.四边形是的外切四边形,若,则的度数是 .
2.如图,,是的两条切线,切点分别为,,连接,,若,则 °.
3.如图,是的切线,是切点,分别交于,两点,若,则 .
4.如图,A是外一点,分别与相切于点B,C.P是上任意一点,过点P作的切线,交于点M,交于点N.,则的周长是 ,若,则 .
【题型5 利用切线长定理进行证明】
1.如图,是的直径,,是的两条切线,切点分别为B,C.连接交于点D,交于点E,连接.
(1)求证:;
(2)若点E是的中点,的半径为6,求的长.
2.如图,,是的切线,,为切点,连接.
(1)若与相切于点,求证;
(2)若,求证与相切.
3.如图,在中,为直径,点M为延长线上的一点,与相切于点C,圆周上有另一点D与点C分居直径两侧,且使得,连接.
求证:①与相切;
②四边形是__________形;
③__________.
4.如图1所示,为的外接圆,为直径,、分别与相切于点D、C().E在线段上,连接并延长与直线相交于点P,B为中点.
(1)证明:是的切线.
(2)如图2,连接,,求证:.
【题型6 利用切线长定理求内切圆半径】
1.如图,在中,,,,则的内切圆半径 .
2.如图,将刻度尺、含角的直角三角板和量角器如图摆放(无重叠部分),若三角板角的顶点A在刻度尺上的读数是,量角器与刻度尺接触点在刻度尺上的读数是,量角器与三角板的接触点为B.
(1) .
(2)该量角器的直径长为 .(结果保留根号)
3.如图,在四边形中,分别与相切于B、E、A三点,为的直径.若,则的半径为 .
4.如图, 内切于正方形,边、上两点,,且是的切线,当的面积为时,则的半径是 .
【题型7 作三角形的内切圆】
1.如图,在的正方形网格中,有部分网格线被擦去.点,,在格点(正方形网格的交点)上.
(1)请用无刻度的直尺在图1中找到三角形的外心;
(2)请用无刻度的直尺在图2中找到三角形的内心.
2.为建设绿色花园城市,某小区要在一块等边空地内修建一个圆形花坛.
(1)实践与操作:要使花坛面积最大,用尺规作图法画出圆形花坛示意图(保留作图痕迹,不要求写作法);
(2)应用与计算:在(1)的条件下,米,求圆形花坛的面积.
3.如图,点C,D分别在射线OA、OB上,求作⊙P,使它与OA、OB、CD都相切.(使用直尺、圆规、直角板作图并保留作图痕迹)
4.按着要求画图.
(1)在图1中,利用直尺和圆规,作出的内切圆(不写作法,保留作图痕迹);
(2)如图2,由小正方形构成的网格中,每个正方形的顶点叫做格点.的顶点都在格点上,经过、、三点,仅用无刻度的直尺在给定的网格中按要求作图(不写作法,保留作图痕迹).
①在图2中,找出的圆心.
②在图2中的边上找到一点,使得平分;
③在图2备用图中的上找到一点(不与点重合),使得.
【题型8 三角形内切圆中求最值】
1.如图,矩形的顶点A,C分别在x轴、y轴上,点B的坐标为,是的内切圆,点N,点P分别是,x轴上的动点,则的最小值是 .
2.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
3.如图,点B的坐标为,以O点为圆心,以为半径的圆交y轴于点A,点C为第一象限圆上一动点,轴于D点,点I为的内心,则的最小值为 .
4.如图,以的斜边为直径作,为的内心,点为上一个动点,为的中点,若,,则的最大值为 .
【题型9 三角形周长、面积与内切圆半径的关系】
1.如图,已知中,,为的内切圆,若,且的面积为24,则的周长为( )
A.48 B. C.24 D.
2.如图,是的内切圆,若的周长为18,面积为9,则的半径是( )
A.1 B. C.1.5 D.2
3.如图,在中,,为中线,若,,设与的内切圆半径分别为,,则的值为( )
A. B. C. D.
4.小明准备以“青山看日出”为元素为永嘉县某名宿设计标志示意图,如图所示,他利用两个等边三角形和一个圆分别表示青山和日出,已知点,,,在同一条直线上,且,四边形和四边形的面积之差为,则的长是 ;连结,若是的内切圆,则圆心到的距离是 .
【题型10 三角形的内切圆与外接圆的综合】
1.如图,中,,,内心为I,连接并延长交的外接圆于D,若,则 ( )
A. B.1 C. D.
2.一个三角形三边长分别为5,12,13,R是其外接圆半径,r是其内切圆半径,则R﹣r= .
3.如图,I是的内心,的延长线交的外接圆于点D.
(1)求证:;
(2)求证:;
(3)连接、,求证:点D是的外心.
4.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.
(1)求证:DG是⊙O的切线;
(2)若DE=4,BE=5,求DI的长.
参考答案
【题型1 利用切线长定理求线段长度】
1.D
【分析】连接,,,,,,交于点M,根据“从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角”可得,,,结合求得点E是中点,然后由等腰三角形三线合一的性质求得点A,O,E共线,在中由勾股定理求得后,利用的面积求得内切圆的半径;由切线长定理和等腰三角形三线合一的性质可得垂直平分,在中由勾股定理求得后,再利用面积法求得即可解答;
【详解】解:如下图,连接,,,,,,交于点M,
由切线长定理可知平分,,
∵,
∴,
∴,
同理根据切线长定理可知平分,,,
∴,
∴点E是中点,
根据等腰三角形三线合一的性质可得点E在的延长线上,即点A,O,E共线,
∴,
中由勾股定理可得,
∵且,
∴,
中由勾股定理可得,
等腰中由三线合一的性质可得垂直平分,
∵,
∴,
∴,
故选: D.
2.B
【分析】本题考查了切线的性质定理,切线长定理,勾股定理,根据切线长定理,得到,根据切线性质,得,勾股定理计算即可.
【详解】∵是的切线,为切点,经过圆心,,
∴,,,
∴,
故选:B.
3.D
【知识点】根据正方形的性质与判定求线段长、切线的性质定理、应用切线长定理求解
【分析】设与正方形的边,切于点F,H,先证四边形是正方形,求出,再根据切线长定理可得.
【详解】解:如图,设与正方形的边,切于点F,H,
则,
,,
四边形是正方形,
的半径为4,且,
,,
,
与相切于点E,
,
故选D.
4.C
【知识点】用勾股定理解三角形、根据矩形的性质与判定求线段长、利用垂径定理求值、应用切线长定理求解
【分析】作于H,由垂径定理得到的长,从而求出的长,由勾股定理求出的长,即可求出的长.
【详解】解:作于H,
∵直径于H,
∴,
∵,分别切于C,B,
∴,直径,
∴四边形是矩形,
∴,,
∴,
∴,
∴.
故选:C.
【题型2 利用切线长定理求周长】
1.C
【分析】本题主要考查切线长定理,熟练掌握切线长定理是解题的关键.
根据切线长定理得到,根据即可得到的周长.
【详解】解:如图:∵的内切圆分别与相切于点,且,
∴,
∵,
∴,
∴的周长,
故选:C.
2.C
【知识点】等边三角形的性质、切线的性质定理、应用切线长定理求解
【分析】本题主要考查了切线的性质和切线长定理,根据切线长定理可知的周长,连接在中,由勾股定理求出的长即可得出结论
【详解】解:连接,如图,
∵是等边三角形,
∴
∵是的中点,
∴,
∵分别切于点M,N,
∴,
同理:,
∴的周长,
在中,,
∴的周长为,
故选:C
3.B
【分析】本题考查切线长定理,勾股定理;利用切线长定理得出,,,再根据三角形周长等于4,可求得,从而利用勾股定理可求解.
【详解】解:∵,是的切线,切点分别是,,
∴,
∵、是的切线,切点是D,交,于点,,
∴,,
∵的周长为4,即,
∴,
∵,
∴,
故选:B.
4.C
【知识点】等边三角形的性质、用勾股定理解三角形、切线的性质定理、应用切线长定理求解
【分析】连接,,根据切线长定理和切线性质、勾股定理求得,根据垂线段最短可得,当时,最小,求出最小值为,当点D与点B(或C)重合时,AD最长,此时,即可得出,从而可求得l最大与是最小值,即可得出答案.
【详解】解:连接,,设切于G,
∵,分别是的切线,
∴,
∵是的切线,
∴,,
∴,
∴周长,
∵是的切线,
∴,
∴,
∴,
∴当最小时,l最小,当最大时,l最大;
根据垂线段最短可得,当时,最小,
∵是边长为3的等边三角形,,
∴,
由勾股定理得:,
当点D与点B(或C)重合时,AD最长,此时,
∴,
∴.
故选:C.
【题型3 利用切线长定理求面积】
1.C
【分析】本题考查切线的性质,正方形的性质,勾股定理,关键是掌握切线长定理.
当半圆面积最大,即M与A重合时,娱乐区的面积最大,由切线长定理得到,,由勾股定理列出关于的方程,求出的长即可解决问题.
【详解】解:当半圆面积最大,即M与A重合时,娱乐区的面积最大,与半圆相切于H,交于P,
∵四边形是正方形,
∴,
∴分别是半圆的切线,
∴,
设,则,,,
在中,,
∴,
∴,
∴,
∴娱乐区的最大面积梯形的面积.
故选:C.
2.20
【分析】直接利用切线长定理得出,,,设,再结合勾股定理得出的长,进而得出答案.
本题考查了切线长定理和勾股定理,解决本题的关键是正确理解题意,熟练掌握切线长定理的相关内容,找到线段之间的关系.
【详解】的内切圆分别与斜边、直角边、切于点D、E、F,,,
,,,
设,
则
整理得,,
解得:,(不合题意舍去),
则, ,
,
故的面积为20,
故答案为20.
3.B
【知识点】应用切线长定理求解
【分析】先根据切线长定理得出,然后利用面积求出OF的长度,即可得到圆的半径,最后利用梯形的面积公式 即可求出梯形的面积.
【详解】连接OF,
∵直线分别与⊙相切于,
∴ .
在 和 中,
∴,
∴.
在 和 中,
∴,
∴.
∵ ,
.
∵,
.
,
∴ ,
,
∴梯形的面积为
.
故选:B.
4.(1)证明:如图所示,连接.
∵是直径,
∴
∴
,都是的切线,
,
;
又,,
,
.
.
(2)如图,连接.
当以,,,四点为顶点的四边形是正方形时,,
∴;
∵
∴,
∴
∵
.
(3)若,则
∵
∴
∴,即
∵ ,
∴,
在中,,
∴,
∴
【题型4 利用切线长定理求角度】
1.
【分析】本题主要考查了切线长定理,解题的关键是熟练掌握切线长定理及其推论.令四边形与分别相切于点E、F、G、H,连接,通过证明,即可求解.
【详解】解:令四边形与分别相切于点E、F、G、H,
连接,
∵是的外切四边形,
∴,
∵,
∴,
∴,
同理可得:,
∵,
∴,
∴,
∴,
故答案为:.
2.
【分析】本题考查了切线的性质以及切线长定理.根据题意可得,,进而求得,根据等边对等角,即可求解.
【详解】解:,是的两条切线,
,,
,
,
,
.
故答案为:.
3.
【分析】本题考查了切线的性质定理以及切线长定理,连接,由切线的性质可求出,再由切线长定理可得出,可求得答案.
【详解】解:如图,连接,
∵分别为的切线,
∴,
∴,
∵为的切线,
∴,
∴,
故答案为:.
4.
【分析】本题考查切线的性质、切线长定理,圆周角定理,先利用勾股定理可计算出的长,再根据切线长定理得到得到的周长,由四边形的内角和得到的度数,然后利用圆周角定理计算是解题的关键.
【详解】解:连接,,,
∵分别与切于点B,C,
∴,,,
在中,,
∵与相切于P,
∴,
∴的周长.
∵,,
∴,
∴,
∴优弧的度数为,
∴,
故答案为:,.
【题型5 利用切线长定理进行证明】
1.(1)证明:∵,是的两条切线,切点分别为,,
∴,,
∴,,
∵,
∴是的中位线,
∴;
(2)∵,点是的中点,
∴,
∴为等边三角形,
∴,
∴,
∵是的切线,
∴,
∵的半径为6,
∴,
∴,
∴.
2.(1)证明:∵与相切,切点为,且,是的切线,,为切点,
∴ ,,
∵,
∴;
(2)证明:延长到点,使得,连接,过点作,垂足为G,连接,,,,
∵,,
∴ ,
∵,是的切线,,为切点,
∴,,
∵,,,
∴,
∴,
又∵,,
∴,
∴,
∴平分,
又∵,,
∴,
∴与相切.
3.
解:①证:连接OC,OD
在和中
,
,
,
是的切线,
,
∴与相切;
②由①可知:,
又∵CM=DM,AM=AM,
∴,
∴AC=AD,
∵AC=AD=CM=MD,
∴四边形是菱形;
故答案为:菱;
③∵AM=CM,OC=OD,
∴,,
∵,
∴,
∵与相切,
∴,
∴,
又∵是菱形,
∴ ,
∴,
故答案为:.
4.(1)证明:连接,
∵为直径,
∴.
在中,B为中点,
∴,
∴,
∵,
∴,
又∵为切线,
∴,
∴
∴.
即,
∴是的切线.
(2)证明:∵、、分别与相切于点D、E、C,
∴,,,,
∴,
∴,
∴,
∴,
∴;
【题型6 利用切线长定理求内切圆半径】
1.1
【分析】本题考查了切线长定理,圆的切线的性质,正方形的判定与性质,熟练掌握切线长定理是解答本题的关键,首先利用切线的性质证明四边形是正方形,得到,再利用切线长定理得到,,最后由列方程即可求解.
【详解】设的内切圆与、、分别相切于点D、E、F,
,,
,
四边形是矩形,
,
四边形是正方形,
,
,,
,,
,,
在中,,
,
,
解得 .
故答案为:1.
2. 2
【分析】本题考查了切线长定理,含30度角直角三角形的特征,勾股定理.根据题意得出和与量角器相切,则,,进而得出,即可解答.
【详解】解:令量角器与刻度尺接触点为点C,量角器圆心为点O,
根据题意可知,和与量角器相切,
∴,,,
∵A在刻度尺上的读数是,C在刻度尺上的读数是,
∴,
∵,
∴,
∵,
∴,
∴,
根据勾股定理可得:,
∴该量角器的直径长为,
故答案为:2,.
3.
【分析】本题考查了切线的性质,切线长定理,勾股定理,矩形的判定与性质,根据切线的性质把图形分割为矩形和直角三角形是解题的关键.
过D作于F,由切线的性质得四边形是矩形,则;由切线长定理可得的长,由勾股定理即可求解.
【详解】解:如图,过D作于F,
∵与,
∴,
∴,
∴四边形是矩形,
∴,
∴;
∵分别与相切,
∴,
∴;
在中,由勾股定理得:,
∴,
∴的半径为.
故答案 为:
4.
【分析】设正方形的边长为,则,设,,则,,,利用勾股定理得出,再由,得出,从而求出,得到.
【详解】解:设与相切于,与相切于,与相切于,
设正方形的边长为,
,
设,,
在中,
,,,
,
,
,
,
,
,
的半径为,
故答案为:.
【题型7 作三角形的内切圆】
1.解:(1)如图,点即为所求;
(2)如图,点即为所求.
2.(1)解:所作图形如图所示:
(2)解:∵是等边三角形,
∴米,,
∵平分,
∴米,
∴米,
由作图可知点O为的内切圆的圆心,也是的重心,
∴米,
∴圆形花坛的面积为.
3.解:如图,作∠DOC的平分线OM,∠ODC的平分线DN,OM交DN于点P1,作P1F⊥OD,以P1为圆心,P1F为半径作⊙P1即可;同法作出⊙P2.
,即为所求;
4.(1)解:如图,即为的内切圆;
(2)解:①圆心如下图所示;
②点如下图所示;
③点如下图所示.
【题型8 三角形内切圆中求最值】
1.4
【分析】延长到点,使,则点与点关于轴对称,则,过点作轴于点,连接交轴于点,交于点,则,当,,,在一条直线上时,取得最小值;利用点的坐标的特征求得线段,,利用三角形的面积关系求得的半径,延长交于点,利用矩形的性质和勾股定理求得的长度,则结论可得.
【详解】解:如图,延长到点,使,则点与点关于轴对称,则,过点作轴于点,连接交轴于点,交于点,则,当,,,在一条直线上时,取得最小值,
点的坐标为,
点的坐标为,
,,
设与三边的切点为,,,连接,,,则,,,设,
,
,
,
,
,
延长交于点,
,,
,,
,,
,
,
的最小值为4.
故答案为:4.
2.
【分析】由矩形的性质得出,,由勾股定理得出,设△的内切圆的半径为,则,解得,连接,易证是的中位线,得出,当经过圆心时,最长,则此时最长,作于,于,则,,由勾股定理得出,则,即可得出结果.
【详解】解:四边形是矩形,
,,
,
设△的内切圆的半径为,
则,
解得:,
连接,
是边上的中点,点是的中点,
是的中位线,
,
当经过圆心时,最长,则此时最长,
作于,于,
则,,
,
,
;
故答案为:.
3.
【分析】连接,作的外接圆,圆心为P,根据内心定义证明,可得,当A,I,P三点共线时,取得最小值,此时,然后根据勾股定理即可解决问题.
【详解】解:如图,连接,作的外接圆,圆心为P,连接,,
∵点I为的内心,
∴,
在和中,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵点B的坐标为,
∴,
∴,
∴P,
当A,I,P三点共线时,取得最小值,
此时
.
故答案为:.
4.
【分析】此题考查了三角形的内切圆和外接圆,连接,,,取中点,连接,过作于点,则点在以点为圆心,为半径的圆上运动,当点三点共线时,最大值为,然后由勾股定理求出的值即可,解题的关键是熟练掌握切线长定理,三角形中位线性质定理和勾股定理的应用.
【详解】解:如图,连接,,,取中点,连接,过作于点,
∵,,,
∴由勾股定理得:,
∵为的中点,
∴,
则点在以点为圆心,为半径的圆上运动,
当点三点共线时,最大,为的值,
∵为的内心,过作于点,于点,
∴四边形为正方形,
由直角三角形的内切圆半径为,即,
∴,
取的中点G,连接,
∴,,
∵,
∴,
∴,
∴,
在中,由勾股定理得:
,
∴最大值为,
故答案为:.
【题型9 三角形周长、面积与内切圆半径的关系】
1.C
【分析】本题考查了三角形内切圆的性质及正方形的判定和性质.
设的半径为r,与的三边、、的切点分别为D、E、F,连接、、.先证四边形是正方形,则,根据勾股定理求出r.又由 的周长内切圆半径,即可求出的周长.
熟练掌握“三角形内切圆的圆心是三条角平分线的交点,它到三角形三条边的距离相等”这一性质,并且能求出内切圆的半径是解题的关键.
【详解】解:如图,设的半径为,与的三边、、的切点分别为,连接、、,则,,,且,
又,
∴四边形是正方形,
,
,
,
解得,
,
,
,即的周长为,
故选:C.
2.A
【分析】作辅助线如解析图,根据,代入数据求解即可.
【详解】解:如图,设与的各边分别相切于点E、F、G,连接,设的半径为r,
则,,
∵
,
又的周长为18,面积为9,
∴,
∴,
故选:A.
3.C
【分析】此题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半,三角形的内切圆和面积,设的内切圆为,与 分别相切于点,由,,得,,连接,由可得,即得,同理得,进而即可求解,正确地作出辅助线是解题的关键.
【详解】解:设的内切圆为,与 分别相切于点,
∵,,,
∴,
,
∵为斜边上的中线,
∴,
∴,
连接,,,,,,则,
∵ ,且,,,
∴,
解得,
同理可得,,
解得,
∴,
故选:C.
4.
【分析】设,表示出相关线段的长,根据四边形和四边形的面积之差,得到,求出值即可;连结,连接并延长交于点,设圆与的切点为,连接,连接,作,垂足为,证明为直角三角形,求出内切圆半径,再根据切线长定理得到,从而证明,求出,从而得到即可.
【详解】解: ,
设,则,
,,
与为等边三角形,
,,
,
,
,
,
.
连结,连接并延长交于点,设圆与的切点为,连接,连接,作,垂足为,
等边的边长为,为中点,
,,
,
,
,
,,
,
,
,,
,
,为直角三角形,
内切圆半径,
,
,
,
,,
,
,
,
,
,
圆心到的距离为,
故答案为:,.
【题型10 三角形的内切圆与外接圆的综合】
1.D
【分析】设的外接圆的圆心为O,连接,,,,根据圆周角定理证得是等边三角形,再根据垂径定理可得,,再根据三角形内心证得,进而解决问题.
【详解】解:如图,设的外接圆的圆心为O,连接,,,,
在中,,,内心为I,
∴平分,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,,
∵I是的内心,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故选:D.
2.4.5
【分析】根据勾股定理的逆定理推出,连接,,根据圆是的内切圆,得到,,,,推出正方形,设,得到方程,求出方程的解即可,进而得出其外接圆的半径,即可得出答案
【详解】如图:连接,
,
圆是的内切圆
,,,
四边形是正方形
设
直角三角形斜边长是直角三角形外接圆的直径
其外接圆半径为:
故答案为:
3.(1)证明:点I是的内心,
平分,
,
,
,
.
(2)证明:如图,连接,
点I是的内心,
平分,平分,
,
又,
,
,,
,
.
(3)证明:如图,连接,,,
,
.
,
∴点D是的外心.
4.(1)证明:连接OD.
∵点I是△ABC的内心,
∴∠2=∠7,
∴ = ,
∴OD⊥AC,
又∵∠1=∠ADF,∠2=∠ABC,∠ADF=∠ABC,
∴∠1=∠2,
∵∠3=∠2,
∴∠1=∠3,
∴DGAC;
∴OD⊥DG,
∴DG是⊙O的切线;
(2)解:∵点I是△ABC的内心,
∴∠5=∠6,
∵∠4=∠7+∠5=∠3+∠6,
即∠4=∠DAI,
∴DA=DI;
∵∠3=∠7,∠AED=∠BAD,
∴△DAE∽△DBA,
∴AD:DB=DE:DA,即AD:9=4:AD,
∴AD=6,
∴DI=6.
