九年级数学下册试题 第三章《圆》复习题--圆中常用辅助线的作法--北师大版(含解析)
文档属性
| 名称 | 九年级数学下册试题 第三章《圆》复习题--圆中常用辅助线的作法--北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 21:51:25 | ||
图片预览




文档简介
第三章《圆》复习题--圆中常用辅助线的作法
【题型1 遇弦连半径构造三角形】
1.如图,内接于,为的直径,点在上,连接、,,延长到点,使得,连接.
(1)求证:;
(2)若⊙O的半径为,,求的长.
2.如图,AB是的直径,弦,垂足为点P,若,,则的直径为( )
A.10 B.8 C.5 D.3
3.如图,是 的外接圆,且 过点 B作,垂足为点E, 延长交于点D, 连接, 并延长交于点F.
(1)写出图中一个与相等的角∶ ;
(2)求证∶
(3)若 , 求的半径.
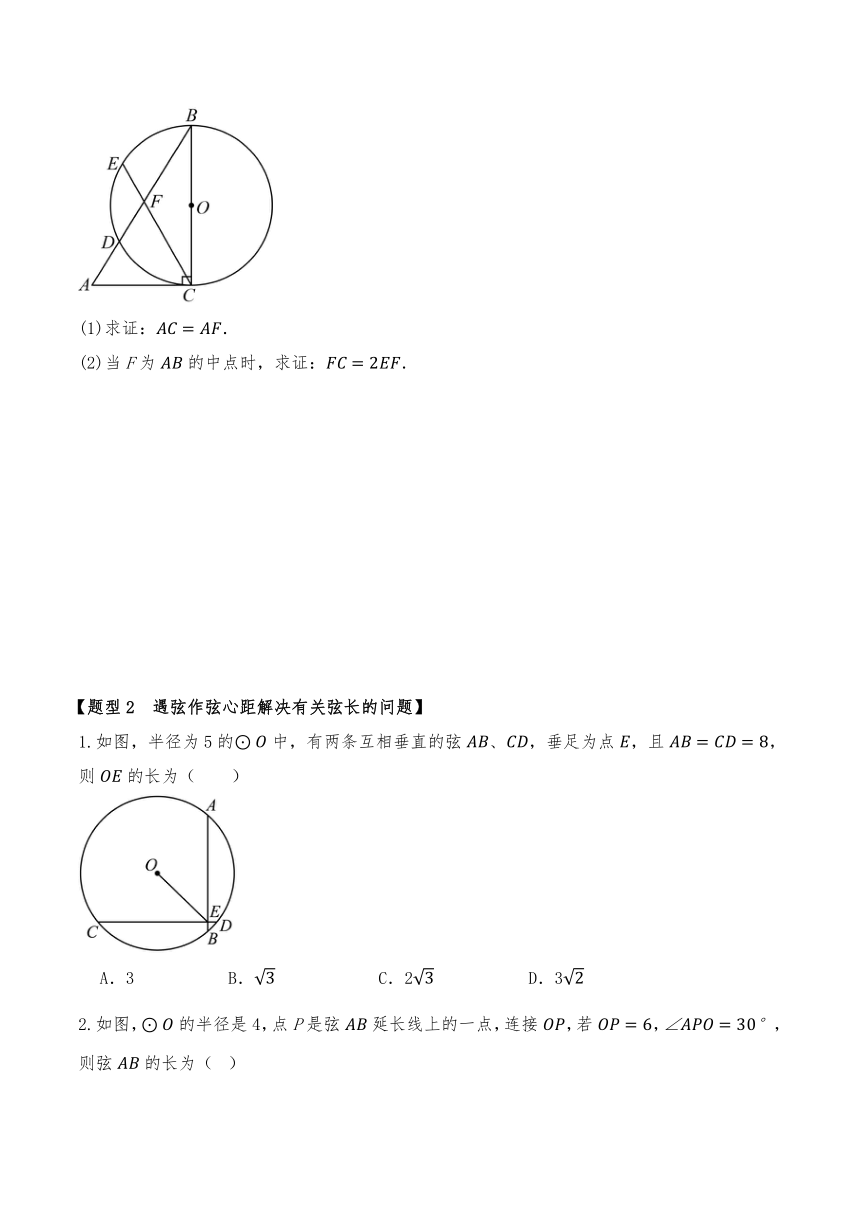
4.如图,在中,,是的直径,与边交于点D,E为的中点,连接,与交于点F.
(1)求证:.
(2)当F为的中点时,求证:.
【题型2 遇弦作弦心距解决有关弦长的问题】
1.如图,半径为5的中,有两条互相垂直的弦、,垂足为点,且,则的长为( )
A.3 B. C.2 D.3
2.如图,的半径是4,点P是弦延长线上的一点,连接,若,,则弦的长为( )
A. B. C.5 D.
3.如图,和相交于和,过点作的平行线交两圆于,已知,则 .
4.关于x的一元二次方程,如果a、b、c满足且,那么我们把这样的方程称为“勾系方程”,请解决下列问题:
(1)求证:关于x的“勾系方程”必有实数根.
(2)如图,已知、是半径为5的的两条平行弦,,,且关于x的方程 是“勾系方程”.
①求的度数,
②直接写出的长:_____________(用含a、b的式子表示).
【题型3 遇直径作直径所对的圆周角】
1.如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
2.如图,为的直径,点C为的中点,交直线于D点.
(1)求证:;
(2)若,求的直径.
3.如图,已知中,,,,点是边上的动点,以为直径作,连接交于点,则的最小值为 .
4.如图,是半圆的直径,,点在半圆上,,是弧上的一个动点,连接,过点作于,连接,在点移动的过程中,的最小值是 .
【题型4 遇切线作过切点的半径】
1.如图,在中,,点P为边上一点,连接,分别以点A,P为圆心,大于是的长为半径画弧,两弧交于点E,F,交于点D,再以点D为圆心,长为半径作圆,交于点M,恰好是的切线.若,,则的长为( )
A. B. C. D.
2.如图,内接于,是的直径与交于点F,,过B点的切线交的延长线于点E.
(1)若,求的度数;
(2)的半径是3,,求的长.
3.已知与相切于点,直线与相交于,两点,为的中点,连接并延长,交的延长线于点.
(1)如图①,若为的中点,求的大小;
(2)如图②,连接与相交于点,求证:.
4.如图,为的直径,,分别切于点,,交的延长线于点,的延长线交于点,于点.若,.
(1)求证:;
(2)求的半径长.
(3)求线段的长.
【题型5 遇90°的圆周角连直径】
1.如图,四边形内接于,,,过点C作,使得,交的延长线于点E.
(1)求证:.
(2)若,求的长.
2.如图,矩形内接于,则 的长为( )
A. B. C. D.
3.《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的边长为2.以它的对角线的交点为位似中心,作它的位似图形,若,则四边形的外接圆半径为 .
4.如图,在平面直角坐标系中,经过点O,与y轴交于点,与x轴交于点,则的长为 .
【题型6 转移线段】
1.如图,的直径,弦,且弦在圆上滑动(的长度不变,点C、D与点A、B不重合),过点C作于点P,若M是的中点,则的最大值是 .
2.如图,在中,,,,经过点C且与边相切的动圆与、分别相交于点P、Q,则线段长度的最小值是 .
3.【问题情境】
如图,是外的一点,直线分别交于点、.
小明认为线段是点到上各点的距离中最短的线段,他是这样考虑的:在上任意取一个不同于点的点,连接、,则有,即,由得,即,从而得出线段是点到上各点的距离中最短的线段.
小红认为在图中,线段是点到上各点的距离中最长的线段,你认为小红的说法正确吗?请说明理由.
【直接运用】
如图,在中,,,以为直径的半圆交于,是上的一个动点,连接,则的最小值是______;
【构造运用】
如图,在边长为的菱形中,,是边的中点,是边上一动点,将沿所在的直线翻折得到,连接,请求出长度的最小值.
【深度运用】
如图,已知点在以为直径,为圆心的半圆上,,以为边作等边,则的最大值是________.
4.如图,以为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为上一动点,于F,点E在G的运动过程中,线段的长度的最小值为 .
【题型7 构造相似三角形】
1.如图,四边形内接于,为直径,平分,,与交于点E, 延长交于点 F.
(1)直接写出线段与线段的数量关系;
(2)求证:;
(3)设的面积为,的面积为,求的值.
2.已知是的直径,.点A是圆外一点,点D和点E在同一条直线上.且.过点A另一条直线交于B、C.
(1)如图1,当时,研究发现:连接、可以得到,继而可以求长.请写出完整的解答过程.
(2)如图2,当B、C重合于一点时,______.
(3)如图3,当平分时,______.
3.如图,以为直径的与相切于点,点在左侧圆弧上,弦交于点,连接,,点关于的对称点为,直线交于点,交于点.
(1)求证:;
(2)当点在上,连接交于点,若,求的值;
(3)当点在射线上,,四边形中有一组对边平行时,求的长.
4.已知是的一条弦,点在上,连接并延长,交弦于点,且.
(1)如图1,如果平分,求证:;
(2)如图2,如果,求的值;
(3)延长线段交弦于点,如果是等腰三角形,且的半径长等于2,求弦的长.
【题型8 四点共圆】
1.如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
2.如图,已知中,,,,,过点作的垂线,与的延长线交于点,则的最大值为( )
A.4 B.5 C. D.
3.如图,在中,,AB=AC=5,点在上,且,点E是AB上的动点,连结,点,G分别是BC,DE的中点,连接,,当AG=FG时,线段长为( )
A. B. C. D.4
4.在中,,点在上方,连接,将绕点顺时针旋转90°到.
(1)如图1,,点在右上方,连接,,若,,,求的长;
(2)如图2,点在的左侧上方,连接交于点,为上一点,若,且为的中点,过作于点,求证:;
(3)如图3,,,,将沿着直线翻折至连接,连接并延长交于点,交于点,当最长时,直接写出此时的面积.
参考答案
【题型1 遇弦连半径构造三角形】
1.(1)证明:∵,,
∴,
∴,,
∵,
∴,
∵,
∴;
(2)解:连接,则,如图所示:
∵,
∴,
∴,,
在中,,在中,,
∴,
解得,
∵,,
∴为的中位线,
∴.
2.A
【分析】连接OC,由垂径定理可得CP=PD=4,然后再根据勾股定理可得OC,进而问题可求解.
【详解】解:连接OC,如图所示:
∵,,
∴CP=PD=4,
∵,
∴在Rt△CPO中,
,
∴的直径为10;
故选A.
3.(1)(答案不唯一)
(2)见解析
(3)的半径为
【分析】本题考查圆周角定理,垂径定理及其推论,相似三角形的判定与性质;
(1)根据圆周角可得;
(2)延长交于,根据垂径定理的推论可得,,即可由得到,进而得到,由三线合一即可得到
(3)连,由勾股定理求得,进而依次得到,,,再求出,最后在中利用勾股定理求半径即可.
【详解】(1)由圆周角可得:,
故答案为:(答案不唯一);
(2)延长交于,
∵延长交于点F
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴
(3)连,
∵,
∴,
∴,
∴,
∴
∴,
∴
中,,
∴
解得,
∴的半径为.
4.(1)连接,交于点N,如图,
∵E为的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)连接,如图,
∵在中,F为的中点,
∴,
∴,
∵E为的中点,
∴,
∴,
∴,
∵是的直径,
∴,
∴,
又∵,
∴,
∴,
即,
∴,
∵,且在(1)已证明,
即.
【题型2 遇弦作弦心距解决有关弦长的问题】
1.D
【分析】作于,于,连接,,根据垂径定理得出,,根据勾股定理求出和证明四边形是正方形,即可解决问题.
【详解】解:如图,作于,于,连接,.
∴,,
∵,
∴,
∴,
∵,
∴,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
故选:.
2.A
【分析】本题主要考查垂径定理,勾股定理,含的直角三角形,连接,则,过点O作交于点D,则可计算出,利用勾股定理求出,进一步利用垂径定理即可求出弦的长.
【详解】解:连接,则,过点O作交于点D,
∵若,
∴,
则=
∴.
故选:A.
3.
【分析】本题考查了矩形的性质和判定,垂径定理的应用,作于点,于点,利用垂径定理得到,,且易得四边形为矩形,进而得到,再利用等量代换即可得到.
【详解】解:作于点,于点,
,,,
,
易得四边形为矩形,
,
,
,
故答案为:.
4.(1)证明:关于的一元二次方程是“勾系方程”,
且,,
,
,
,
方程必有实数根;
(2)解:①,理由如下:
作于,延长交于,连接,
,
,
,
,
,
是“勾系方程”,
,
;
,
;
,
,
,
,
.
②如图所示,过点作的垂线,垂足为,则四边形是矩形,
∴,
∵,则
∴
故答案为:.
【题型3 遇直径作直径所对的圆周角】
1.(1)解:,
,
,
是的直径,,
,
,
故的度数为;
(2)证明:连接,,
是的切线,
,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
,
.
2.(1)证明:连接,如图,
∵为的直径,
∴,即,
∵点C为的中点,
∴,
∴,
∴;
(2)解:设交于点T,如图,
∵,
∴,
∴四边形是矩形,
∴,
∵,
∴,
设,
则,
∴,
∴,即的直径为5;
3.
【分析】连接,由以为直径作,得,,即可得动点在以为直径的圆上运动,当,,在一直线上时,根据,即可求解.
【详解】解:中,,,,
连接,由以为直径作,,,
,,
动点在以为直径的圆上运动,为圆心,
当,,在一直线上时,
即的最小值为
故答案为:.
4.
【分析】连接,取的中点,连接,由题意先判断出点在以点为圆心,为半径的圆上,当、、三点共线时,取得最小值,然后利用勾股定理,求出的长,再利用勾股定理,求出的长,再利用直角三角形中,斜边上的中线等于斜边的一半,求出的长,再由,即可算出的长.
【详解】解:如图,连接,取的中点,连接,
∵,
∴点在以点为圆心,为半径的圆上,当、、三点共线时,取得最小值,
∵是直径,
∴,
在中,
∵,,
∴由勾股定理得:,
∵为的中点,
∴,
在中,
∵,,
∴由勾股定理得:,
又∵,且点为的中点,
∴,
∴.
故答案为:.
【题型4 遇切线作过切点的半径】
1.A
【分析】本题考查的是切线的性质、含角的直角三角形的性质,相似三角形的判定与性质,掌握圆的切线垂直于经过切点的半径是解题的关键.连接,由线段垂直平分线的性质可得,再由直角三角形性质求得,根据切线的性质得到,再证明,再列出方程求解即可.
【详解】解:连接,
由题意可得,是的垂直平分线,
,
设,
,,
,
是的切线,
,
,
,
,
,
,
,
,
,
,
,
故选:A
2.(1)解:连接,
∵是的切线
∴
∴
∵
∴
∵
∴
∴
∴
(2)解:连接,
∵
∴
∴
∵
∴
∵
∴
∴
∵
∴
∴
在中,,
根据勾股定理得,
设,由,得,
解得,
∴的长为4.
3.(1)解:连接,如图①,
与相切于点,
,
,
为的中点,
,
,
在中,,
,
点为的中点,
,
,
;
(2)证明:连接,如图②,
点为的中点,
,
,
,,
,
,
,
.
4.(1)证明:连接,
,是的切线,
,,
在和中,
,
,
,
,
,
,,
,
.
(2)解:由(1)得:,
,
,
在中,根据勾股定理得:
,
在中,设,
则,,
由勾股定理得:,
即:,
解得:,
,
即的半径为3.
(3)解:在和中,根据勾股定理得:
,
,
,,
,
,即:,
.
【题型5 遇90°的圆周角连直径】
1.(1)证明:如图,连接.
,
,
.
,
,.
,,
,
.
在与中,
,
.
(2)解:如图,连接.
,
是的直径,
.
由(1)可得.
,
.
在中,;
在中,.
2.B
【分析】本题考查了圆的基础知识,如图,连接,根据内接矩形的性质可得是直径,根据直角三角形斜边中线等于斜边上的高,可得,可得是等边三角形,再根据弧长的计算方法即可求解,掌握矩形的性质,圆的基础值,弧长计算公式是解题的关键.
【详解】解:如图所示,连接,
∵四边形是矩形,
∴,
∴是直径,点是线段的中点,
∴在中,,
∴,
∴,
∴是等边三角形,
∴,
∴
故选:B .
3.
【分析】本题考查位似图形的性质,根据正方形的边长为2和位似比求出,进而即可求解.解题关键求出正方形的边长.
【详解】解:如图,连接,
∵正方形与四边形是位似图形,
∴四边形是正方形,
∴是四边形的外接圆直径,
∵正方形的边长为2,
∴四边形的外接圆半径为,
故答案为:.
4.5
【分析】本题考查了90度圆周角所对的弦为直径,勾股定理,连接,通过题意判断出为直径,圆心P在上,根据勾股定理计算出的长,从而得出结果.
【详解】解:如图,连接,
为直角,且点都在圆上,
为直径,圆心P在上,
, ,
,,
,
,
故答案为:5.
【题型6 转移线段】
1.4
【分析】本题考查垂径定理、三角形中位线定理,延长交于点K,连接,根据垂径定理可得,再根据三角形中位线定理可得,进而可得当最大时,的值最大,即即当为直径时,的值最大,即可求解.
【详解】解:延长交于点K,连接,
∵,
∴,
∵M是的中点,
∴是的中位线,
∴,
∴当最大时,的值最大,
即当为直径时,的值最大,
∵的直径,
∴,
故答案为:4.
2.
【分析】设圆心为点F,圆F与的切点为D,连接、、,则有,由勾股定理的逆定理可得,再由直角三角形的性质可得,又由,为圆F的直径,可得点F在直角三角形的斜边的高上时,有最小值,即为圆F的直径,再利用的面积即可求解.
【详解】解:如图,设圆心为点F,圆F与的切点为D,连接、、,
∵圆F与相切,
∴,
∵在中,,即,
∴,
∴,
又∵,
∴,
∵,为圆F的直径,
∴当点F在直角三角形的斜边的高上时,有最小值,即为圆F的直径,
∵,
∴,
∴,
故答案为:.
3.解:问题情境∶小红的说法正确,
在圆О上任意取一个不同于点的点,连接、,
∵在中,>PC OB=OC,
∴>,即>.
∴线段是点Р到圆О上各点的距离中最长的线段.
∴小红的说法正确;
直接运用∶取半圆的圆心,连接交半圆于点,则当与点重合时,最小,
∵,,
∴,,
∴,
∴的最小值为
故答案为:.
构造运用:由折叠知,
∵是的中点,
∴,
∴点,,都在以为直径的圆上.如图,以点为圆心,为半径画,连接.
当长度取最小值时,点在上,
过点作于点,
∵在边长为的菱形中,
,为中点,
∴,,
∴,
∴.
∴,
∴,
;
深度运用:如图,在的上方作等边,连接,取的中点连接,
∵是半圆的直径,
∴,
∵和都是等边三角形,
∴,,即,
∴,
∴,
∴,
∴点在以为直径的半圆上,
∵是的中点,,
∴,,
∴,
∴根据三角形的两边之和大于第三边可得的最大值为,
故答案为:.
4.
【分析】本题主要考查垂径定理,圆周角定理,直角三角形度角的判定和性质,熟练掌握性质定理,构造直角三角形是解题的关键.过点作于点,连接.得到点在的延长线上时,的长度的最小,最小值,即可得到答案.
【详解】解:过点作于点,连接,
,
,
,
,
在中,,
,
,
,
,
,
,
,
,
,
点在以为直径的上,
,
点在的延长线上时,的长度的最小,最小值,
故答案为:.
【题型7 构造相似三角形】
1.(1)解:连接,则:,
∵平分,
∴,
∴,
∴,
∴;
(2)∵为直径,
∴,
∴,
又∵,,
∴;
(3)过点作,则
∵为直径,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
2.(1)解:连接、,如图所示:
∵,,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
解得:.
(2)解:连接,如图所示:
∵当B、C重合于一点时,与相切于点C,
∴,
∵,
∴,
∴,
∴.
(3)解:连接,如图所示:
∵平分,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
根据解析(1)可知:,
∴,
∵,
∴,
∴,
即,
解得:,,
∴.
3.(1)证明:如图,设与相交于点M,
∵与相切于点A,
∴,
∵,
∴,
∴,
∴,,
∵点A关于的对称点为E,
∴,
∴.
(2)解:过F点作于点K,设与交于点N,连接,如下图所示:
由同弧所对的圆周角相等可知:,
∵为的直径,且,由垂径定理得:,
∴,
∵点A关于的对称点为E,
∴,
∴,即,
∴,
由同弧所对的圆周角相等得:,且,
∴,
∴,
∵,与交于点N,
∴.
∵,,
∴,
∴,
设,
∵点A关于的对称点为E,
,,,
又,
∴,
∴.
∵,
∴,
∴;
(3)解:分类讨论如下:
如图,当时,连接,,设,则,
∵,
,
,
,
,
,
,
,,
,
,
,
∵,
,
,
,
;
如图,当时,连接,,
设,
,
∵,
,
,
,
,
,
,
,
,
,
,
;
综上所述,满足条件的的长为或,
4.(1)证明:如图1中,
平分,
,
,
,,
,
,
∴,
,
= .
(2)解:如图2中,作于,于,设.
,
,
四边形是矩形,
,
,,
,
,,
,,
,
,
,
,
,
,
,,
,,,
.
(3)解:如图中,当时,
,
,
,
,
,
,
,
,
∴,
,
,
,
解得或(舍弃),
.
如图中,当时,可得是等腰直角三角形,
,
,
,
,
综上所述,的值为或.
【题型8 四点共圆】
1.解:(1)BF=,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=(360°﹣∠BFE)=(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=FG.
故答案为:BF=FG;
(2)①如图2所示,
②;理由如下:
如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=FG,
∴DF=FG.
2.C
【分析】由,,证明,推出,当有最大值时,有最大值,根据,得到点A、C、B、P四点共圆,若有最大值,则应为直径,由,得到是圆的直径,勾股定理求出,即可得到答案.
【详解】解:∵
∴
∵
∴
∴
∴
∴,
∴当有最大值时,有最大值,
∵,
∴点A、C、B、P四点共圆,
若有最大值,则应为直径,
∵,
∴是圆的直径,
∴,
∴的最大值为,
故选:C.
3.A
【分析】连接DF,EF,过点F作FN⊥AC,FM⊥AB,结合直角三角形斜边中线等于斜边的一半求得点A,D,F,E四点共圆,∠DFE=90°,然后根据勾股定理及正方形的判定和性质求得AE的长度,从而求解.
【详解】解:连接DF,EF,过点F作FN⊥AC,FM⊥AB
∵在中,,点G是DE的中点,
∴AG=DG=EG
又∵AG=FG
∴点A,D,F,E四点共圆,且DE是圆的直径
∴∠DFE=90°
∵在Rt△ABC中,AB=AC=5,点是BC的中点,
∴CF=BF=,FN=FM=
又∵FN⊥AC,FM⊥AB,
∴四边形NAMF是正方形
∴AN=AM=FN=
又∵,
∴
∴△NFD≌△MFE
∴ME=DN=AN-AD=
∴AE=AM+ME=3
∴在Rt△DAE中,DE=
故选:A.
4.(1)如图①,过A点作于G,
∵将绕点D顺时针旋转到,
∴是等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(2)如图,过F点作于,过点B作于J,
∴,
∴,
∵,
∴四边形是矩形,
∴,,,
∴,
∵,
∴,
∴,
∵M点为的中点,
∴,
又∵,,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
即.
(3)的面积是1
如图3,连接,
∵,,
∴,
由翻折可知,,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴点A、R、B、C在以为直径的圆上,
∴当时,的值最大,
∵,
∴,
∴的最大值为,此时,是直径,
由,,
此时,四边形是正方形,如图4所示,
∴,
由翻折知:
∴,
∵,
∴,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
过D点作,垂足为E,
∵,
∴,
∴,
∴,
∴.
【题型1 遇弦连半径构造三角形】
1.如图,内接于,为的直径,点在上,连接、,,延长到点,使得,连接.
(1)求证:;
(2)若⊙O的半径为,,求的长.
2.如图,AB是的直径,弦,垂足为点P,若,,则的直径为( )
A.10 B.8 C.5 D.3
3.如图,是 的外接圆,且 过点 B作,垂足为点E, 延长交于点D, 连接, 并延长交于点F.
(1)写出图中一个与相等的角∶ ;
(2)求证∶
(3)若 , 求的半径.
4.如图,在中,,是的直径,与边交于点D,E为的中点,连接,与交于点F.
(1)求证:.
(2)当F为的中点时,求证:.
【题型2 遇弦作弦心距解决有关弦长的问题】
1.如图,半径为5的中,有两条互相垂直的弦、,垂足为点,且,则的长为( )
A.3 B. C.2 D.3
2.如图,的半径是4,点P是弦延长线上的一点,连接,若,,则弦的长为( )
A. B. C.5 D.
3.如图,和相交于和,过点作的平行线交两圆于,已知,则 .
4.关于x的一元二次方程,如果a、b、c满足且,那么我们把这样的方程称为“勾系方程”,请解决下列问题:
(1)求证:关于x的“勾系方程”必有实数根.
(2)如图,已知、是半径为5的的两条平行弦,,,且关于x的方程 是“勾系方程”.
①求的度数,
②直接写出的长:_____________(用含a、b的式子表示).
【题型3 遇直径作直径所对的圆周角】
1.如图,是的直径,是的一条弦,于点M,连接.
(1)若,求的度数;
(2)的延长线相交于点F,是的切线,交于点E,若,求证:.
2.如图,为的直径,点C为的中点,交直线于D点.
(1)求证:;
(2)若,求的直径.
3.如图,已知中,,,,点是边上的动点,以为直径作,连接交于点,则的最小值为 .
4.如图,是半圆的直径,,点在半圆上,,是弧上的一个动点,连接,过点作于,连接,在点移动的过程中,的最小值是 .
【题型4 遇切线作过切点的半径】
1.如图,在中,,点P为边上一点,连接,分别以点A,P为圆心,大于是的长为半径画弧,两弧交于点E,F,交于点D,再以点D为圆心,长为半径作圆,交于点M,恰好是的切线.若,,则的长为( )
A. B. C. D.
2.如图,内接于,是的直径与交于点F,,过B点的切线交的延长线于点E.
(1)若,求的度数;
(2)的半径是3,,求的长.
3.已知与相切于点,直线与相交于,两点,为的中点,连接并延长,交的延长线于点.
(1)如图①,若为的中点,求的大小;
(2)如图②,连接与相交于点,求证:.
4.如图,为的直径,,分别切于点,,交的延长线于点,的延长线交于点,于点.若,.
(1)求证:;
(2)求的半径长.
(3)求线段的长.
【题型5 遇90°的圆周角连直径】
1.如图,四边形内接于,,,过点C作,使得,交的延长线于点E.
(1)求证:.
(2)若,求的长.
2.如图,矩形内接于,则 的长为( )
A. B. C. D.
3.《墨子·天文志》记载:“执规矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形的边长为2.以它的对角线的交点为位似中心,作它的位似图形,若,则四边形的外接圆半径为 .
4.如图,在平面直角坐标系中,经过点O,与y轴交于点,与x轴交于点,则的长为 .
【题型6 转移线段】
1.如图,的直径,弦,且弦在圆上滑动(的长度不变,点C、D与点A、B不重合),过点C作于点P,若M是的中点,则的最大值是 .
2.如图,在中,,,,经过点C且与边相切的动圆与、分别相交于点P、Q,则线段长度的最小值是 .
3.【问题情境】
如图,是外的一点,直线分别交于点、.
小明认为线段是点到上各点的距离中最短的线段,他是这样考虑的:在上任意取一个不同于点的点,连接、,则有,即,由得,即,从而得出线段是点到上各点的距离中最短的线段.
小红认为在图中,线段是点到上各点的距离中最长的线段,你认为小红的说法正确吗?请说明理由.
【直接运用】
如图,在中,,,以为直径的半圆交于,是上的一个动点,连接,则的最小值是______;
【构造运用】
如图,在边长为的菱形中,,是边的中点,是边上一动点,将沿所在的直线翻折得到,连接,请求出长度的最小值.
【深度运用】
如图,已知点在以为直径,为圆心的半圆上,,以为边作等边,则的最大值是________.
4.如图,以为圆心,半径为6的圆与x轴交于A,B两点,与y轴交于C,D两点,点E为上一动点,于F,点E在G的运动过程中,线段的长度的最小值为 .
【题型7 构造相似三角形】
1.如图,四边形内接于,为直径,平分,,与交于点E, 延长交于点 F.
(1)直接写出线段与线段的数量关系;
(2)求证:;
(3)设的面积为,的面积为,求的值.
2.已知是的直径,.点A是圆外一点,点D和点E在同一条直线上.且.过点A另一条直线交于B、C.
(1)如图1,当时,研究发现:连接、可以得到,继而可以求长.请写出完整的解答过程.
(2)如图2,当B、C重合于一点时,______.
(3)如图3,当平分时,______.
3.如图,以为直径的与相切于点,点在左侧圆弧上,弦交于点,连接,,点关于的对称点为,直线交于点,交于点.
(1)求证:;
(2)当点在上,连接交于点,若,求的值;
(3)当点在射线上,,四边形中有一组对边平行时,求的长.
4.已知是的一条弦,点在上,连接并延长,交弦于点,且.
(1)如图1,如果平分,求证:;
(2)如图2,如果,求的值;
(3)延长线段交弦于点,如果是等腰三角形,且的半径长等于2,求弦的长.
【题型8 四点共圆】
1.如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
2.如图,已知中,,,,,过点作的垂线,与的延长线交于点,则的最大值为( )
A.4 B.5 C. D.
3.如图,在中,,AB=AC=5,点在上,且,点E是AB上的动点,连结,点,G分别是BC,DE的中点,连接,,当AG=FG时,线段长为( )
A. B. C. D.4
4.在中,,点在上方,连接,将绕点顺时针旋转90°到.
(1)如图1,,点在右上方,连接,,若,,,求的长;
(2)如图2,点在的左侧上方,连接交于点,为上一点,若,且为的中点,过作于点,求证:;
(3)如图3,,,,将沿着直线翻折至连接,连接并延长交于点,交于点,当最长时,直接写出此时的面积.
参考答案
【题型1 遇弦连半径构造三角形】
1.(1)证明:∵,,
∴,
∴,,
∵,
∴,
∵,
∴;
(2)解:连接,则,如图所示:
∵,
∴,
∴,,
在中,,在中,,
∴,
解得,
∵,,
∴为的中位线,
∴.
2.A
【分析】连接OC,由垂径定理可得CP=PD=4,然后再根据勾股定理可得OC,进而问题可求解.
【详解】解:连接OC,如图所示:
∵,,
∴CP=PD=4,
∵,
∴在Rt△CPO中,
,
∴的直径为10;
故选A.
3.(1)(答案不唯一)
(2)见解析
(3)的半径为
【分析】本题考查圆周角定理,垂径定理及其推论,相似三角形的判定与性质;
(1)根据圆周角可得;
(2)延长交于,根据垂径定理的推论可得,,即可由得到,进而得到,由三线合一即可得到
(3)连,由勾股定理求得,进而依次得到,,,再求出,最后在中利用勾股定理求半径即可.
【详解】(1)由圆周角可得:,
故答案为:(答案不唯一);
(2)延长交于,
∵延长交于点F
∴,,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴
(3)连,
∵,
∴,
∴,
∴,
∴
∴,
∴
中,,
∴
解得,
∴的半径为.
4.(1)连接,交于点N,如图,
∵E为的中点,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
(2)连接,如图,
∵在中,F为的中点,
∴,
∴,
∵E为的中点,
∴,
∴,
∴,
∵是的直径,
∴,
∴,
又∵,
∴,
∴,
即,
∴,
∵,且在(1)已证明,
即.
【题型2 遇弦作弦心距解决有关弦长的问题】
1.D
【分析】作于,于,连接,,根据垂径定理得出,,根据勾股定理求出和证明四边形是正方形,即可解决问题.
【详解】解:如图,作于,于,连接,.
∴,,
∵,
∴,
∴,
∵,
∴,
∴四边形是矩形,
∵,
∴四边形是正方形,
∴,
故选:.
2.A
【分析】本题主要考查垂径定理,勾股定理,含的直角三角形,连接,则,过点O作交于点D,则可计算出,利用勾股定理求出,进一步利用垂径定理即可求出弦的长.
【详解】解:连接,则,过点O作交于点D,
∵若,
∴,
则=
∴.
故选:A.
3.
【分析】本题考查了矩形的性质和判定,垂径定理的应用,作于点,于点,利用垂径定理得到,,且易得四边形为矩形,进而得到,再利用等量代换即可得到.
【详解】解:作于点,于点,
,,,
,
易得四边形为矩形,
,
,
,
故答案为:.
4.(1)证明:关于的一元二次方程是“勾系方程”,
且,,
,
,
,
方程必有实数根;
(2)解:①,理由如下:
作于,延长交于,连接,
,
,
,
,
,
是“勾系方程”,
,
;
,
;
,
,
,
,
.
②如图所示,过点作的垂线,垂足为,则四边形是矩形,
∴,
∵,则
∴
故答案为:.
【题型3 遇直径作直径所对的圆周角】
1.(1)解:,
,
,
是的直径,,
,
,
故的度数为;
(2)证明:连接,,
是的切线,
,
,
,
,
,
,
,
,
是的直径,
,
,
,
,
,
.
2.(1)证明:连接,如图,
∵为的直径,
∴,即,
∵点C为的中点,
∴,
∴,
∴;
(2)解:设交于点T,如图,
∵,
∴,
∴四边形是矩形,
∴,
∵,
∴,
设,
则,
∴,
∴,即的直径为5;
3.
【分析】连接,由以为直径作,得,,即可得动点在以为直径的圆上运动,当,,在一直线上时,根据,即可求解.
【详解】解:中,,,,
连接,由以为直径作,,,
,,
动点在以为直径的圆上运动,为圆心,
当,,在一直线上时,
即的最小值为
故答案为:.
4.
【分析】连接,取的中点,连接,由题意先判断出点在以点为圆心,为半径的圆上,当、、三点共线时,取得最小值,然后利用勾股定理,求出的长,再利用勾股定理,求出的长,再利用直角三角形中,斜边上的中线等于斜边的一半,求出的长,再由,即可算出的长.
【详解】解:如图,连接,取的中点,连接,
∵,
∴点在以点为圆心,为半径的圆上,当、、三点共线时,取得最小值,
∵是直径,
∴,
在中,
∵,,
∴由勾股定理得:,
∵为的中点,
∴,
在中,
∵,,
∴由勾股定理得:,
又∵,且点为的中点,
∴,
∴.
故答案为:.
【题型4 遇切线作过切点的半径】
1.A
【分析】本题考查的是切线的性质、含角的直角三角形的性质,相似三角形的判定与性质,掌握圆的切线垂直于经过切点的半径是解题的关键.连接,由线段垂直平分线的性质可得,再由直角三角形性质求得,根据切线的性质得到,再证明,再列出方程求解即可.
【详解】解:连接,
由题意可得,是的垂直平分线,
,
设,
,,
,
是的切线,
,
,
,
,
,
,
,
,
,
,
,
故选:A
2.(1)解:连接,
∵是的切线
∴
∴
∵
∴
∵
∴
∴
∴
(2)解:连接,
∵
∴
∴
∵
∴
∵
∴
∴
∵
∴
∴
在中,,
根据勾股定理得,
设,由,得,
解得,
∴的长为4.
3.(1)解:连接,如图①,
与相切于点,
,
,
为的中点,
,
,
在中,,
,
点为的中点,
,
,
;
(2)证明:连接,如图②,
点为的中点,
,
,
,,
,
,
,
.
4.(1)证明:连接,
,是的切线,
,,
在和中,
,
,
,
,
,
,,
,
.
(2)解:由(1)得:,
,
,
在中,根据勾股定理得:
,
在中,设,
则,,
由勾股定理得:,
即:,
解得:,
,
即的半径为3.
(3)解:在和中,根据勾股定理得:
,
,
,,
,
,即:,
.
【题型5 遇90°的圆周角连直径】
1.(1)证明:如图,连接.
,
,
.
,
,.
,,
,
.
在与中,
,
.
(2)解:如图,连接.
,
是的直径,
.
由(1)可得.
,
.
在中,;
在中,.
2.B
【分析】本题考查了圆的基础知识,如图,连接,根据内接矩形的性质可得是直径,根据直角三角形斜边中线等于斜边上的高,可得,可得是等边三角形,再根据弧长的计算方法即可求解,掌握矩形的性质,圆的基础值,弧长计算公式是解题的关键.
【详解】解:如图所示,连接,
∵四边形是矩形,
∴,
∴是直径,点是线段的中点,
∴在中,,
∴,
∴,
∴是等边三角形,
∴,
∴
故选:B .
3.
【分析】本题考查位似图形的性质,根据正方形的边长为2和位似比求出,进而即可求解.解题关键求出正方形的边长.
【详解】解:如图,连接,
∵正方形与四边形是位似图形,
∴四边形是正方形,
∴是四边形的外接圆直径,
∵正方形的边长为2,
∴四边形的外接圆半径为,
故答案为:.
4.5
【分析】本题考查了90度圆周角所对的弦为直径,勾股定理,连接,通过题意判断出为直径,圆心P在上,根据勾股定理计算出的长,从而得出结果.
【详解】解:如图,连接,
为直角,且点都在圆上,
为直径,圆心P在上,
, ,
,,
,
,
故答案为:5.
【题型6 转移线段】
1.4
【分析】本题考查垂径定理、三角形中位线定理,延长交于点K,连接,根据垂径定理可得,再根据三角形中位线定理可得,进而可得当最大时,的值最大,即即当为直径时,的值最大,即可求解.
【详解】解:延长交于点K,连接,
∵,
∴,
∵M是的中点,
∴是的中位线,
∴,
∴当最大时,的值最大,
即当为直径时,的值最大,
∵的直径,
∴,
故答案为:4.
2.
【分析】设圆心为点F,圆F与的切点为D,连接、、,则有,由勾股定理的逆定理可得,再由直角三角形的性质可得,又由,为圆F的直径,可得点F在直角三角形的斜边的高上时,有最小值,即为圆F的直径,再利用的面积即可求解.
【详解】解:如图,设圆心为点F,圆F与的切点为D,连接、、,
∵圆F与相切,
∴,
∵在中,,即,
∴,
∴,
又∵,
∴,
∵,为圆F的直径,
∴当点F在直角三角形的斜边的高上时,有最小值,即为圆F的直径,
∵,
∴,
∴,
故答案为:.
3.解:问题情境∶小红的说法正确,
在圆О上任意取一个不同于点的点,连接、,
∵在中,>PC OB=OC,
∴>,即>.
∴线段是点Р到圆О上各点的距离中最长的线段.
∴小红的说法正确;
直接运用∶取半圆的圆心,连接交半圆于点,则当与点重合时,最小,
∵,,
∴,,
∴,
∴的最小值为
故答案为:.
构造运用:由折叠知,
∵是的中点,
∴,
∴点,,都在以为直径的圆上.如图,以点为圆心,为半径画,连接.
当长度取最小值时,点在上,
过点作于点,
∵在边长为的菱形中,
,为中点,
∴,,
∴,
∴.
∴,
∴,
;
深度运用:如图,在的上方作等边,连接,取的中点连接,
∵是半圆的直径,
∴,
∵和都是等边三角形,
∴,,即,
∴,
∴,
∴,
∴点在以为直径的半圆上,
∵是的中点,,
∴,,
∴,
∴根据三角形的两边之和大于第三边可得的最大值为,
故答案为:.
4.
【分析】本题主要考查垂径定理,圆周角定理,直角三角形度角的判定和性质,熟练掌握性质定理,构造直角三角形是解题的关键.过点作于点,连接.得到点在的延长线上时,的长度的最小,最小值,即可得到答案.
【详解】解:过点作于点,连接,
,
,
,
,
在中,,
,
,
,
,
,
,
,
,
,
点在以为直径的上,
,
点在的延长线上时,的长度的最小,最小值,
故答案为:.
【题型7 构造相似三角形】
1.(1)解:连接,则:,
∵平分,
∴,
∴,
∴,
∴;
(2)∵为直径,
∴,
∴,
又∵,,
∴;
(3)过点作,则
∵为直径,
∴,
∵,
∴,
∵,
∴,
∴,
∴.
2.(1)解:连接、,如图所示:
∵,,
∴,
∵,,
∴,
∵,
∴,
∴,
∴,
解得:.
(2)解:连接,如图所示:
∵当B、C重合于一点时,与相切于点C,
∴,
∵,
∴,
∴,
∴.
(3)解:连接,如图所示:
∵平分,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
根据解析(1)可知:,
∴,
∵,
∴,
∴,
即,
解得:,,
∴.
3.(1)证明:如图,设与相交于点M,
∵与相切于点A,
∴,
∵,
∴,
∴,
∴,,
∵点A关于的对称点为E,
∴,
∴.
(2)解:过F点作于点K,设与交于点N,连接,如下图所示:
由同弧所对的圆周角相等可知:,
∵为的直径,且,由垂径定理得:,
∴,
∵点A关于的对称点为E,
∴,
∴,即,
∴,
由同弧所对的圆周角相等得:,且,
∴,
∴,
∵,与交于点N,
∴.
∵,,
∴,
∴,
设,
∵点A关于的对称点为E,
,,,
又,
∴,
∴.
∵,
∴,
∴;
(3)解:分类讨论如下:
如图,当时,连接,,设,则,
∵,
,
,
,
,
,
,
,,
,
,
,
∵,
,
,
,
;
如图,当时,连接,,
设,
,
∵,
,
,
,
,
,
,
,
,
,
,
;
综上所述,满足条件的的长为或,
4.(1)证明:如图1中,
平分,
,
,
,,
,
,
∴,
,
= .
(2)解:如图2中,作于,于,设.
,
,
四边形是矩形,
,
,,
,
,,
,,
,
,
,
,
,
,
,,
,,,
.
(3)解:如图中,当时,
,
,
,
,
,
,
,
,
∴,
,
,
,
解得或(舍弃),
.
如图中,当时,可得是等腰直角三角形,
,
,
,
,
综上所述,的值为或.
【题型8 四点共圆】
1.解:(1)BF=,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=(360°﹣∠BFE)=(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=FG.
故答案为:BF=FG;
(2)①如图2所示,
②;理由如下:
如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=FG,
∴DF=FG.
2.C
【分析】由,,证明,推出,当有最大值时,有最大值,根据,得到点A、C、B、P四点共圆,若有最大值,则应为直径,由,得到是圆的直径,勾股定理求出,即可得到答案.
【详解】解:∵
∴
∵
∴
∴
∴
∴,
∴当有最大值时,有最大值,
∵,
∴点A、C、B、P四点共圆,
若有最大值,则应为直径,
∵,
∴是圆的直径,
∴,
∴的最大值为,
故选:C.
3.A
【分析】连接DF,EF,过点F作FN⊥AC,FM⊥AB,结合直角三角形斜边中线等于斜边的一半求得点A,D,F,E四点共圆,∠DFE=90°,然后根据勾股定理及正方形的判定和性质求得AE的长度,从而求解.
【详解】解:连接DF,EF,过点F作FN⊥AC,FM⊥AB
∵在中,,点G是DE的中点,
∴AG=DG=EG
又∵AG=FG
∴点A,D,F,E四点共圆,且DE是圆的直径
∴∠DFE=90°
∵在Rt△ABC中,AB=AC=5,点是BC的中点,
∴CF=BF=,FN=FM=
又∵FN⊥AC,FM⊥AB,
∴四边形NAMF是正方形
∴AN=AM=FN=
又∵,
∴
∴△NFD≌△MFE
∴ME=DN=AN-AD=
∴AE=AM+ME=3
∴在Rt△DAE中,DE=
故选:A.
4.(1)如图①,过A点作于G,
∵将绕点D顺时针旋转到,
∴是等腰直角三角形,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(2)如图,过F点作于,过点B作于J,
∴,
∴,
∵,
∴四边形是矩形,
∴,,,
∴,
∵,
∴,
∴,
∵M点为的中点,
∴,
又∵,,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
∴,
即.
(3)的面积是1
如图3,连接,
∵,,
∴,
由翻折可知,,
∴,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴点A、R、B、C在以为直径的圆上,
∴当时,的值最大,
∵,
∴,
∴的最大值为,此时,是直径,
由,,
此时,四边形是正方形,如图4所示,
∴,
由翻折知:
∴,
∵,
∴,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,
∴,
过D点作,垂足为E,
∵,
∴,
∴,
∴,
∴.
