第六章平行四边形单元测试卷(含答案)
文档属性
| 名称 | 第六章平行四边形单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 679.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 17:23:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章平行四边形单元测试卷北师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
2.如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7 B.8 C.9 D.10
3.小宇看到一个多边形中,从某一顶点出发的对角线共有3条,那么这个多边形的内角和是( )
A.720° B.540° C.360° D.180°
4.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
5.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P.连接OE,∠ADC=60°,ABBC=1,则下列结论:①∠CAD=30°;②BD=2;③S平行四边形ABCD=AB AC;④AD=4OE.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,分别以△ABC的三边为一边作 BCED, ABFG, ACIH,且点D,E分别在FG,HI上.若 ABFG, ACIH的面积分别为S1,S2,则 BCED的面积为( )
A.S1+S2 B. C. D.
7.如图,∠B+∠C+∠D+∠E﹣∠A等于( )
A.180° B.240° C.300° D.360°
8.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
二.填空题(每小题5分,满分20分)
9.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数为 .
10.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 .
11.在平面直角坐标系中,有四个点O(0,0),A(4,0),B(1,3),C(x,3),若以O、A、B、C为顶点的四边形是平行四边形,则x= .
12.平行四边形两邻边的长为3和4,两对角线长为m,n,则m2+n2的值为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
14.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
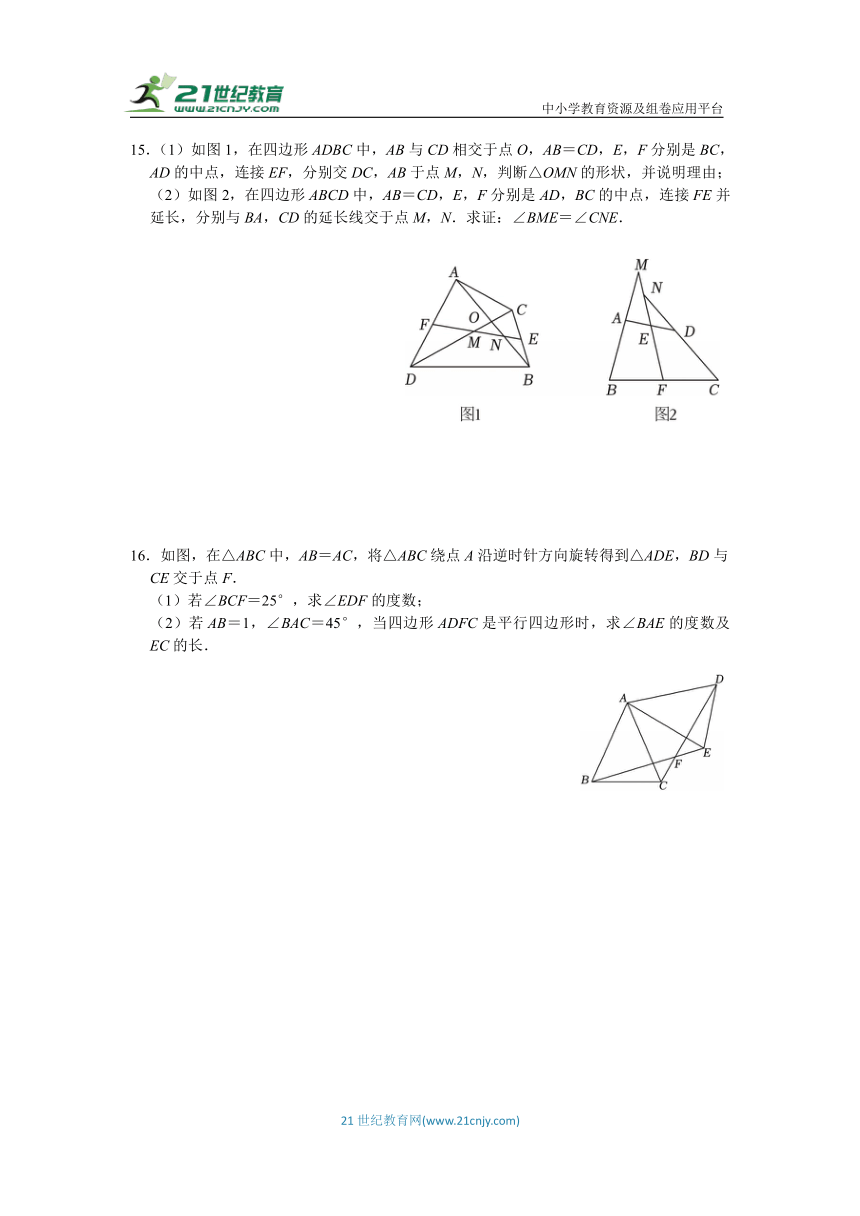
15.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
16.如图,在△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转得到△ADE,BD与CE交于点F.
(1)若∠BCF=25°,求∠EDF的度数;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求∠BAE的度数及EC的长.
17.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
18.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
参考答案
一、选择题
1—8:CDAACAAC
二、填空题
9.【解答】解:由题意得:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故答案为:84°.
10.【解答】解:∵五边形ABCDE是正五边形,
∴其每个内角为108°,且AB=BC,
∴△ABC是等腰三角形,
∴∠BCA=(180°﹣108°)÷2=36°,
∴∠ACD=∠BCE﹣∠BCA=108°﹣36°=72°.
故答案为:72°
11.【解答】解:∵B(1,3),C(x,3),
∴BC∥x轴,
∵以O,A,B,C为顶点的四边形是平行四边形,O(0,0),A(4,0),
∴BC=OA=4,
①当点C在点B左侧,如图1,则x=1﹣4=﹣3;
②当点C在点B右侧,如图2,则x=1+4=5;
综上所述,x=﹣3或5,
故答案为:﹣3或5.
12.【解答】解:设 ABCD中,AB=3,BC=4,AC=m,BD=n,
作AE⊥BC,DF⊥BC,垂足分别为E,F,如图所示,
在 ABCD中,AD∥BC,CD=AB=3,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=90°,AE∥DF,
∴四边形AEFD是平行四边形,
∴AE=DF,EF=AD=BC=4,
∴BE=CF,
在Rt△ABE中,AE2+BE2=AB2=9,
在Rt△AEC中,AE2+EC2=AC2=m2,
在Rt△DCF中,DF2+CF2=CD2=9,
在Rt△BFD中,DF2+BF2=BD2=n2,
∴m2+n2
=AE2+EC2+DF2+BF2
=AE2+(4﹣BE)2+DF2+(4+CF)2
=AE2+16﹣8BE+BE2+DF2+16+8CF+CF2
=32+(AE2+BE2)+(DF2+CF2)
=32+9+9
=50,
故答案为:50.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
14.【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
15.【解答】解:(1)△OMN是等腰三角形,理由如下:
如图,取BD的中点H,连接HE,HF,
∵E,F分别是BC,AD的中点,
∴HF∥AB,HE∥CD,,,
∵AB=CD,
∴HF=HE,
∴∠HFE=∠HEF,
∵HF∥AB,HE∥CD,
∴∠HFE=∠ONM,∠HEF=∠OMN,
∴∠ONM=∠OMN,
∴OM=ON,
∴△OMN是等腰三角形.
(2)如图,连接BD,取BD的中点H,连接HE,HF,
∴HF∥CN,HE∥BM,,,
∵AB=CD,
∴HF=HE,
∴∠HEF=∠HFE,
∵HF∥CN,HE∥BM,
∴∠HEF=∠BME,∠HFE=∠CNE,
∴∠BME=∠CNE.
16.【解答】解:(1)连接BE.
∵将△ABC绕点A沿顺时针旋转得到△ADE,
∴AD=AB,AC=AE,∠BAC=∠DAE,
∴∠DAB=∠EAC,
又∵AB=AC,AD=AB,AC=AE,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS),
∴EC=BD.
在△DEB和△CBE中,
,
∴△DEB≌△CBE(SSS).
∴∠EDF=∠ECB=25°;
(2)由旋转性质得∠DAE=BAC=45°,AB=AC=AD=AE=1,
∵四边形ADFC是平行四边形,
∴AC∥DF.
∴∠ABD=∠BAC=45°,
∵AD=AB=1,
∴∠ADB=∠ABD=45°.
∴∠DAB=90°.
∵∠BAC=∠DAE=45°,
∴∠BAE=45°
由勾股定理,可求得,
∵△AEC≌△ADB,
∴.
17.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
18.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
21世纪教育网(www.21cnjy.com)
第六章平行四边形单元测试卷北师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
2.如果一个正多边形的内角和是外角和的4倍,那么这个正多边形的边数为( )
A.7 B.8 C.9 D.10
3.小宇看到一个多边形中,从某一顶点出发的对角线共有3条,那么这个多边形的内角和是( )
A.720° B.540° C.360° D.180°
4.观察图,根据所标注的数据能判断其一定是平行四边形的是( )
A.只有③ B.只有② C.①② D.①②③
5.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,分别交BC,BD于点E、P.连接OE,∠ADC=60°,ABBC=1,则下列结论:①∠CAD=30°;②BD=2;③S平行四边形ABCD=AB AC;④AD=4OE.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
6.如图,分别以△ABC的三边为一边作 BCED, ABFG, ACIH,且点D,E分别在FG,HI上.若 ABFG, ACIH的面积分别为S1,S2,则 BCED的面积为( )
A.S1+S2 B. C. D.
7.如图,∠B+∠C+∠D+∠E﹣∠A等于( )
A.180° B.240° C.300° D.360°
8.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
二.填空题(每小题5分,满分20分)
9.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE在同一条直线上,则∠COF的度数为 .
10.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 .
11.在平面直角坐标系中,有四个点O(0,0),A(4,0),B(1,3),C(x,3),若以O、A、B、C为顶点的四边形是平行四边形,则x= .
12.平行四边形两邻边的长为3和4,两对角线长为m,n,则m2+n2的值为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
14.如图,AB⊥CD,垂足为O,点P、Q分别在射线OC、OA上运动(点P、Q都不与点O重合),QE是∠AQP的平分线.
(1)如图1,在点P、Q的运动过程中,若直线QE交∠DPQ的平分线于点H.
①当∠PQB=60°时,∠PHE= °;
②随着点P、Q分别在OC、OA的运动,∠PHE的大小是否是定值?如果是定值,请求出∠PHE的度数;如果不是定值,请说明理由;
(2)如图2,若QE所在直线交∠QPC的平分线于点E时,将△EFG沿FG折叠,使点E落在四边形PFGQ内点E′的位置,猜测∠PFE′与∠QGE′之间的数量关系,并说明理由.
15.(1)如图1,在四边形ADBC中,AB与CD相交于点O,AB=CD,E,F分别是BC,AD的中点,连接EF,分别交DC,AB于点M,N,判断△OMN的形状,并说明理由;
(2)如图2,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE.
16.如图,在△ABC中,AB=AC,将△ABC绕点A沿逆时针方向旋转得到△ADE,BD与CE交于点F.
(1)若∠BCF=25°,求∠EDF的度数;
(2)若AB=1,∠BAC=45°,当四边形ADFC是平行四边形时,求∠BAE的度数及EC的长.
17.如图,在平行四边形ABCD中,点F是AD中点,连接CF并延长交BA的延长线于点E.
(1)求证:AB=AE.
(2)若BC=2AE,∠E=31°,求∠DAB的度数.
18.如图,在△ABC中,AB=AC,AD⊥BC于点D,延长DC到点E,使CE=CD.过点E作EF∥AD交AC的延长线于点F,连接AE,DF.
(1)求证:四边形ADFE是平行四边形;
(2)过点E作EG⊥DF于点G,若BD=2,AE=6,求EG的长.
参考答案
一、选择题
1—8:CDAACAAC
二、填空题
9.【解答】解:由题意得:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故答案为:84°.
10.【解答】解:∵五边形ABCDE是正五边形,
∴其每个内角为108°,且AB=BC,
∴△ABC是等腰三角形,
∴∠BCA=(180°﹣108°)÷2=36°,
∴∠ACD=∠BCE﹣∠BCA=108°﹣36°=72°.
故答案为:72°
11.【解答】解:∵B(1,3),C(x,3),
∴BC∥x轴,
∵以O,A,B,C为顶点的四边形是平行四边形,O(0,0),A(4,0),
∴BC=OA=4,
①当点C在点B左侧,如图1,则x=1﹣4=﹣3;
②当点C在点B右侧,如图2,则x=1+4=5;
综上所述,x=﹣3或5,
故答案为:﹣3或5.
12.【解答】解:设 ABCD中,AB=3,BC=4,AC=m,BD=n,
作AE⊥BC,DF⊥BC,垂足分别为E,F,如图所示,
在 ABCD中,AD∥BC,CD=AB=3,
∵AE⊥BC,DF⊥BC,
∴∠AEB=∠AEC=∠DFB=90°,AE∥DF,
∴四边形AEFD是平行四边形,
∴AE=DF,EF=AD=BC=4,
∴BE=CF,
在Rt△ABE中,AE2+BE2=AB2=9,
在Rt△AEC中,AE2+EC2=AC2=m2,
在Rt△DCF中,DF2+CF2=CD2=9,
在Rt△BFD中,DF2+BF2=BD2=n2,
∴m2+n2
=AE2+EC2+DF2+BF2
=AE2+(4﹣BE)2+DF2+(4+CF)2
=AE2+16﹣8BE+BE2+DF2+16+8CF+CF2
=32+(AE2+BE2)+(DF2+CF2)
=32+9+9
=50,
故答案为:50.
三、解答题
13.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
14.【解答】解:(1)①∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠PQB=60°,
∴∠QPO=30°,∠AQP=120°,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°,
故答案为:45;
②∠PHE 是一个定值,∠PHE=45°,理由如下:
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∴∠QPO=90°﹣∠PQO,∠AQP=180°﹣∠PQO,
∵EQ平分∠AQP,PH平分∠QPO,
∴,,
∴∠H=∠EQP﹣∠HPQ=45°;
(2)∠PFE'+∠QGE'=90°,理由如下:
如图2所示,连接EE',
∵AB⊥CD,
∴∠POQ=90°,
∴∠PQO+∠QPO=90°,
∵∠CPQ+∠QPO=180°,∠PQA+∠PQO=180°,
∴180°﹣∠CPQ+180°﹣∠PQA=90°,
∴∠CPQ+∠PQA=270°,
∵QE,PE分别平分∠PQA,∠CPQ,
∴,
∴,
∴∠PEQ=180°﹣∠EPQ﹣∠EQP=45°,
由折叠的性质可知∠GE'F=∠PEQ=45°,
∵∠FEE'+∠EFE'+∠EE'F=180°=∠GEE'+∠EGE'+∠EE'G,
∴∠FEG+∠FE'G+∠EFE'+∠EGE'=360°,
∴∠EFE'+∠EFE'=270°,
∵∠EFE'+∠PFE'=180°=∠EGE'+∠QGE',
∴∠PFE'+∠QGE'=360°﹣∠EFE'﹣∠EFE'=90°.
15.【解答】解:(1)△OMN是等腰三角形,理由如下:
如图,取BD的中点H,连接HE,HF,
∵E,F分别是BC,AD的中点,
∴HF∥AB,HE∥CD,,,
∵AB=CD,
∴HF=HE,
∴∠HFE=∠HEF,
∵HF∥AB,HE∥CD,
∴∠HFE=∠ONM,∠HEF=∠OMN,
∴∠ONM=∠OMN,
∴OM=ON,
∴△OMN是等腰三角形.
(2)如图,连接BD,取BD的中点H,连接HE,HF,
∴HF∥CN,HE∥BM,,,
∵AB=CD,
∴HF=HE,
∴∠HEF=∠HFE,
∵HF∥CN,HE∥BM,
∴∠HEF=∠BME,∠HFE=∠CNE,
∴∠BME=∠CNE.
16.【解答】解:(1)连接BE.
∵将△ABC绕点A沿顺时针旋转得到△ADE,
∴AD=AB,AC=AE,∠BAC=∠DAE,
∴∠DAB=∠EAC,
又∵AB=AC,AD=AB,AC=AE,
∴AD=AE,
在△AEC和△ADB中,
,
∴△AEC≌△ADB(SAS),
∴EC=BD.
在△DEB和△CBE中,
,
∴△DEB≌△CBE(SSS).
∴∠EDF=∠ECB=25°;
(2)由旋转性质得∠DAE=BAC=45°,AB=AC=AD=AE=1,
∵四边形ADFC是平行四边形,
∴AC∥DF.
∴∠ABD=∠BAC=45°,
∵AD=AB=1,
∴∠ADB=∠ABD=45°.
∴∠DAB=90°.
∵∠BAC=∠DAE=45°,
∴∠BAE=45°
由勾股定理,可求得,
∵△AEC≌△ADB,
∴.
17.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,BC=AD,
∴∠E=∠DCF,
∵点F是AD中点,
∴AF=DF,
∵∠EFA=∠CFD,
∴△AFE≌△DFC(AAS),
∴CD=AE,
∴AB=AE;
(2)解:由(1)可得AF=DF,BC=AD,
∵BC=2AE,
∴AE=AF,
∵∠E=31°,
∴∠AFE=∠E=31°,
∴∠DAB=2∠E=62°.
18.【解答】(1)证明:∵EF∥AD,
∴∠FEC=∠ADC,
又∵CE=CD,∠FCE=∠ACD,
∴△FCE≌△ACD(ASA),
∴EF=AD,
∴四边形ADFE是平行四边形;
(2)解:如图,
由(1)可知,四边形ADFE是平行四边形,
∴DF=AE=6,
∵AB=AC,AD⊥BC,
∴CD=BD=2,
∴CE=CD=2,
∴DE=2CD=4,
∵EF∥AD,
∴EF⊥BC,
∴∠DEF=90°,
∴EF2,
∵EG⊥DF,
∴S△DEFDF EG EF,
∴EG,
即EG的长为.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
