第十九章矩形、菱形、正方形单元测试(一)(含答案)
文档属性
| 名称 | 第十九章矩形、菱形、正方形单元测试(一)(含答案) | 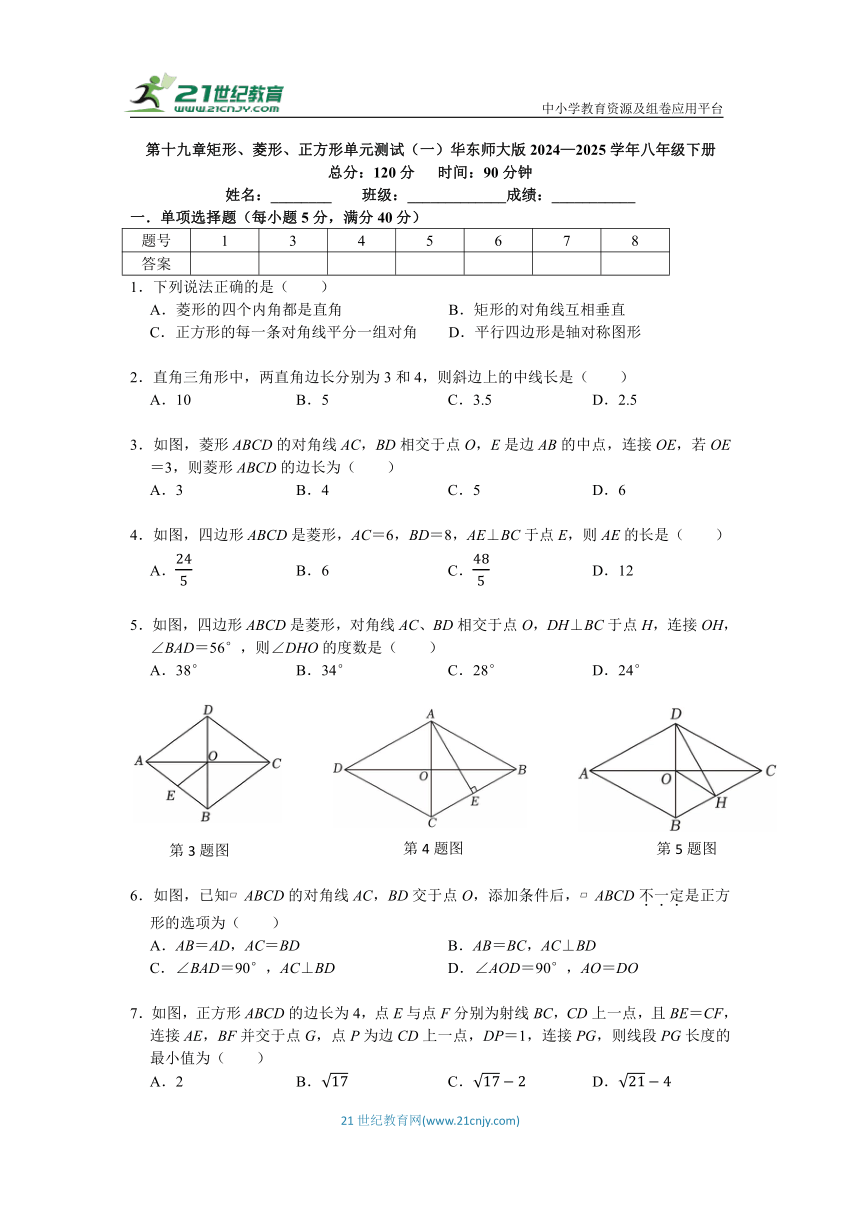 | |
| 格式 | docx | ||
| 文件大小 | 554.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 17:25:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十九章矩形、菱形、正方形单元测试(一)华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
2.直角三角形中,两直角边长分别为3和4,则斜边上的中线长是( )
A.10 B.5 C.3.5 D.2.5
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是边AB的中点,连接OE,若OE=3,则菱形ABCD的边长为( )
A.3 B.4 C.5 D.6
4.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
5.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥BC于点H,连接OH,∠BAD=56°,则∠DHO的度数是( )
A.38° B.34° C.28° D.24°
6.如图,已知 ABCD的对角线AC,BD交于点O,添加条件后, ABCD不一定是正方形的选项为( )
A.AB=AD,AC=BD B.AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD D.∠AOD=90°,AO=DO
7.如图,正方形ABCD的边长为4,点E与点F分别为射线BC,CD上一点,且BE=CF,连接AE,BF并交于点G,点P为边CD上一点,DP=1,连接PG,则线段PG长度的最小值为( )
A.2 B. C. D.
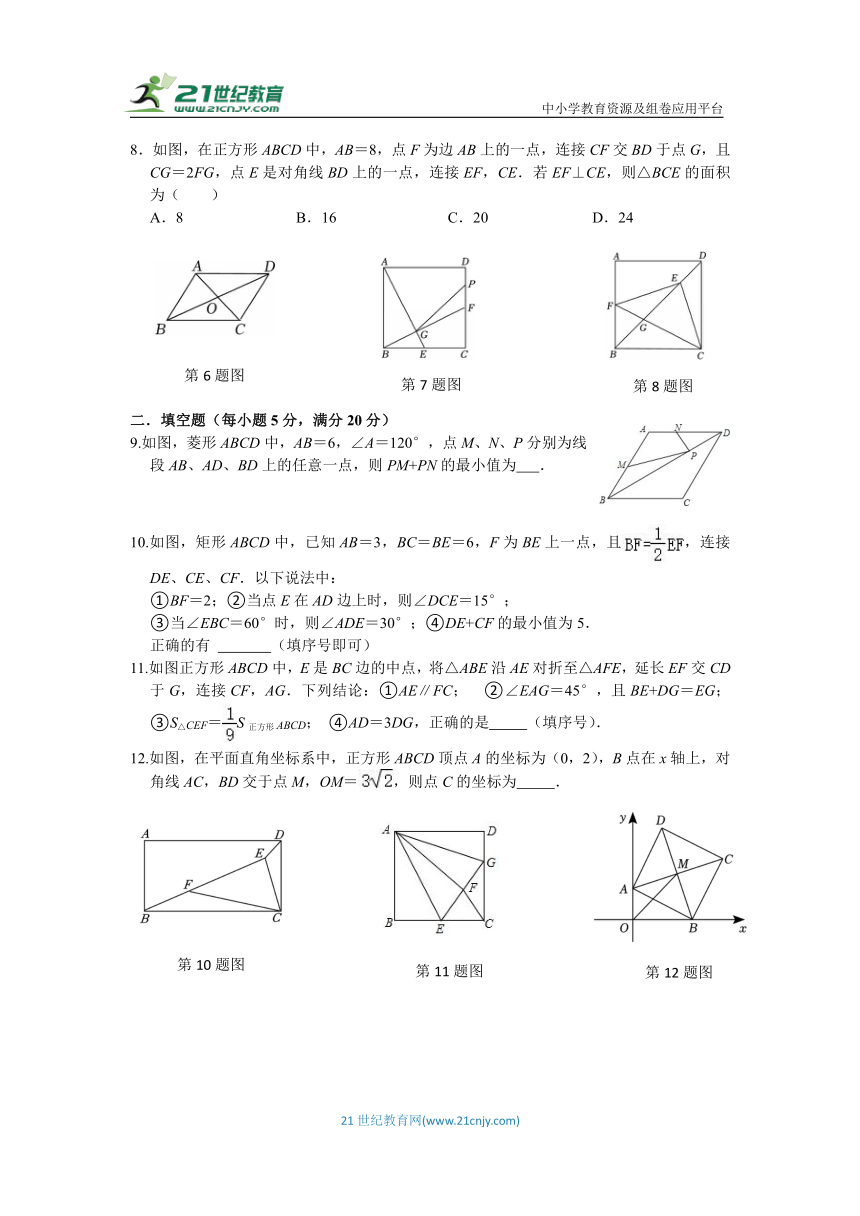
8.如图,在正方形ABCD中,AB=8,点F为边AB上的一点,连接CF交BD于点G,且CG=2FG,点E是对角线BD上的一点,连接EF,CE.若EF⊥CE,则△BCE的面积为( )
A.8 B.16 C.20 D.24
二.填空题(每小题5分,满分20分)
9.如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为 .
10.如图,矩形ABCD中,已知AB=3,BC=BE=6,F为BE上一点,且,连接DE、CE、CF.以下说法中:
①BF=2;②当点E在AD边上时,则∠DCE=15°;
③当∠EBC=60°时,则∠ADE=30°;④DE+CF的最小值为5.
正确的有 (填序号即可)
11.如图正方形ABCD中,E是BC边的中点,将△ABE沿AE对折至△AFE,延长EF交CD于G,连接CF,AG.下列结论:①AE∥FC; ②∠EAG=45°,且BE+DG=EG;③S△CEF=S正方形ABCD; ④AD=3DG,正确的是 (填序号).
12.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点在x轴上,对角线AC,BD交于点M,OM=,则点C的坐标为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,△ABC中,AB=AC,AD平分∠BAC,BE∥AD,AE⊥AD.
(1)求证:四边形ADBE是矩形;
(2)作EF⊥AB于F,若BC=4,AD=3,求EF的长.
14.如图,在四边形ABCD中,AD=AB=BC,AC⊥BD交于点O.
(1)求证:四边形ABCD为菱形;
(2)如图2,过四边形ABCD的顶点A作AE⊥BC于点E,交OB于点H,若AB=AC=6,求四边形OHEC的面积.
15.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
16.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:∠DAE=∠ADE;
(2)求证:△AEB≌△DEC;
(3)当EB=BC时,求∠AFD的度数.
17.如图①正方形ABCD中,点E是对角线AC上任意一点,连接DE,BE.
(1)求证:DE=BE;
(2)当AE=AB时,求∠BED的度数;
(3)如图②,过点E作EF⊥DE交AB于点F,当BE=BF时,若AB.求AF的长.
18.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
参考答案
一、选择题
1—8:CDDACBCD
二、填空题
9.【解答】解:∵四边形ABCD是菱形,
∴AB=AD,
当PM⊥AB,PN⊥AD时,
PM+PN的值最小,最小值=AD边上的高,设这个高为h,
AB PM+ AD PN=AD h,
∴PM+PN=h=AB sin60°=3,
故答案为:
10.【解答】解:∵BE=6,BF=EF,
∴BF=2,EF=4,故①正确;
如图1,当点E在AD上时,取BE的中点H,连接AH,
∵点H是BE的中点,∠BAE=90°,
∴AH=BH=HE=3,
∴AB=AH=BH=3,
∴△ABH是等边三角形,
∴∠ABE=60°,
∴∠EBC=30°,
∵BE=BC,
∴∠BCE=∠BEC=75°,
∴∠DCE=15°,故②正确;
如图2,当∠EBC=60°时,设AD与CE交于H,与BE交于点G,
∵∠EBC=60°,BC=BE,
∴△EBC是等边三角形,
∴∠EBC=∠ECB=60°=∠BEC,
∴∠ABG=∠DCE=30°,
∴AB=AG,CD=DH,
∴AG=DH=,
∴GH=6﹣2,
∵AD∥BC,
∴∠EGH=∠EBC=60°,∠GHE=∠BCE=60°,
∴△GEH是等边三角形,
∴EH=GH=6﹣2≠DH,
∴∠ADE≠∠DEH,
∴∠ADE≠30°;故③错误;
如图3,在BC上截取BM=BF=2,连接EM,DM,
∵BE=BC,∠EBM=∠CBF,
∴△BFC≌△BME(SAS),
∴CF=EM,
∴DE+CF=DE+EM,
∴当点E,点D,点M三点共线时,DE+CF有最小值,最小值为DM的长,
∵CM=BC﹣BM=4,CD=AB=3,
∴DM===5,
∴DE+CF的最小值为5,故④正确;
故答案为:①②④.
11.【解答】解:①∵E是BC边的中点,
∴BE=CE,
由折叠知,∠AEB=∠AEF,BE=EF,
∴CE=EF,
∴∠ECF=∠EFC,
∵∠BEF=∠ECF+∠EFC,
∴∠AEB=∠ECF,
∴AE∥CF,
故①正确;
②由折叠知AB=AF,∠ABE=∠AFE=90°,∠BAE=∠FAE,
∵正方形ABCD中,AB=AD,∠ADG=90°,
∴AD=AF,
∵AG=AG,
∴Rt△ADG≌Rt△AFG(HL),
∴∠DAG=∠FAG,DG=FG
∴∠BAE+∠DAG=∠EAF+∠FAG,BE+DG=EF+FG
∴∠EAG=,BE+DG=EG,
故②正确;
③设正方形ABCD的边长为a,CG=x,则EC=BE=EF=a,GF=DG=a﹣x,
在△CEG中,由勾股定理得,
,
解得,x=a,
∴,
∵EF:EG=a:(a+a﹣a)=3:5,
∴=,
故③错误;
④由上可知DG=a﹣x=a﹣a=a,
∵AD=a,
∴AD=3DG,
故④正确;
故答案为:①②④.
12.【解答】解:过点C作CE⊥x轴于点E,过点M作MF⊥x轴于点F,连接EM,
∴∠MFO=∠CEO=∠AOB=90°,AO∥MF∥CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,AM=CM,
∴∠OAB=∠EBC,OF=EF,
∴MF是梯形AOEC的中位线,
∴MF=(AO+EC),
∵MF⊥OE,
∴MO=ME.
∵在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴OB=CE,AO=BE.
∴MF=(BE+OB),
又∵OF=FE,
∴△MOE是直角三角形,
∵MO=ME,
∴△MOE是等腰直角三角形,
∴OE==6,
∵A(0,2),
∴OA=2,
∴BE=2,
∴OB=CE=4.
∴C(6,4).
故答案为:(6,4).
三、解答题
13.【解答】(1)证明:∵△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADB=90°,
∵BE∥AD,AE⊥AD,
∴∠DBE=90°,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:∵AB=AC,AD平分∠BAC,BC=4,AD=3,
∴.
在直角三角形ABD中,由勾股定理得:.
∵四边形ADBE是矩形,
∴BE=AD=3,AE=BD=2.
∵,
∴.
14.【解答】(1)证明:∵AD=AB,AC⊥BD,
∴AC垂直平分BD,
∴BC=CD,
∴BC=CD=AD=AB,
∴四边形ABCD为菱形;
(2)解:如图,连接CH,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,
∵AB=AC=6,
∴AB=AC=BC=6,
∴△ABC是等边三角形,
∵AE⊥CB,6
∴BE=CE=3,
∴AE,
∵AO=OC,BE=EC,
∴S△AOH=S△OCH=S△ECH=S△BEH,
∴.
15.【解答】(1)证明:∵在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,
∴四边形ABCD是平行四边形,AC=AO+CO=20,
∵AB=12,BC=16,
∴AB2+BC=122+162=202=AC2,
∴∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形
∴∠ADC=90°,
∵∠ADF:∠FDC=3:2,∠ADF+∠FDC=∠ADC,
∴,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
16.【解答】(1)证明:∵ABCD为正方形,
∴∠BAD=90°,
∵点E为DF中点,
∴AE=EF=DEDF,
∴∠EAD=∠EDA;
(2)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,
∵∠EAD=∠EDA,
∵∠BAE=∠BAD﹣∠EAD,∠CDE=∠ADC﹣∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
(3)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°﹣60°=30°,
∵EB=BC=AB,
∴∠BAE(180°﹣30°)=75°,
又∵AE=EF,
∴∠AFD=∠BAE=75°.
17.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠BAE,
∵AE=AE,
∴△DAE≌△BAE(SAS),
∴DE=BE;
(2)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
由(1)知:△DAE≌△BAE,
∴∠AED=∠AEB(180°﹣45°)135°,
∴∠BED=2∠AEB=135°;
(3)如图②,过E作EM⊥BF,
∵四边形ABCD是正方形,
∴CD=CB,∠DCE=∠BCE,
∵CE=CE,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵∠ADC=∠ABC=90°,
∴∠ADE=∠ABE,
∵DE⊥EF,
∴∠DEF=90°,
在四边形ADEF中,∠DAF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠BFE=180°,
∴∠BFE=∠EBF,
∴BE=EF,
∵BE=BF,
∴△BEF是等边三角形,
∴∠EBF=60°,
设BM=x,则MF=BM=x,EMx,
∵四边形ABCD是正方形,
∴∠BAE∠BAD=45°,
∴AM=EMx,
∵AM+BM=AB,
∴xx,
解得,x,
∴BF=2x=2,
∴AF=AB﹣BF2.
18.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
21世纪教育网(www.21cnjy.com)
第十九章矩形、菱形、正方形单元测试(一)华东师大版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.下列说法正确的是( )
A.菱形的四个内角都是直角 B.矩形的对角线互相垂直
C.正方形的每一条对角线平分一组对角 D.平行四边形是轴对称图形
2.直角三角形中,两直角边长分别为3和4,则斜边上的中线长是( )
A.10 B.5 C.3.5 D.2.5
3.如图,菱形ABCD的对角线AC,BD相交于点O,E是边AB的中点,连接OE,若OE=3,则菱形ABCD的边长为( )
A.3 B.4 C.5 D.6
4.如图,四边形ABCD是菱形,AC=6,BD=8,AE⊥BC于点E,则AE的长是( )
A. B.6 C. D.12
5.如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥BC于点H,连接OH,∠BAD=56°,则∠DHO的度数是( )
A.38° B.34° C.28° D.24°
6.如图,已知 ABCD的对角线AC,BD交于点O,添加条件后, ABCD不一定是正方形的选项为( )
A.AB=AD,AC=BD B.AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD D.∠AOD=90°,AO=DO
7.如图,正方形ABCD的边长为4,点E与点F分别为射线BC,CD上一点,且BE=CF,连接AE,BF并交于点G,点P为边CD上一点,DP=1,连接PG,则线段PG长度的最小值为( )
A.2 B. C. D.
8.如图,在正方形ABCD中,AB=8,点F为边AB上的一点,连接CF交BD于点G,且CG=2FG,点E是对角线BD上的一点,连接EF,CE.若EF⊥CE,则△BCE的面积为( )
A.8 B.16 C.20 D.24
二.填空题(每小题5分,满分20分)
9.如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为 .
10.如图,矩形ABCD中,已知AB=3,BC=BE=6,F为BE上一点,且,连接DE、CE、CF.以下说法中:
①BF=2;②当点E在AD边上时,则∠DCE=15°;
③当∠EBC=60°时,则∠ADE=30°;④DE+CF的最小值为5.
正确的有 (填序号即可)
11.如图正方形ABCD中,E是BC边的中点,将△ABE沿AE对折至△AFE,延长EF交CD于G,连接CF,AG.下列结论:①AE∥FC; ②∠EAG=45°,且BE+DG=EG;③S△CEF=S正方形ABCD; ④AD=3DG,正确的是 (填序号).
12.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点在x轴上,对角线AC,BD交于点M,OM=,则点C的坐标为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,△ABC中,AB=AC,AD平分∠BAC,BE∥AD,AE⊥AD.
(1)求证:四边形ADBE是矩形;
(2)作EF⊥AB于F,若BC=4,AD=3,求EF的长.
14.如图,在四边形ABCD中,AD=AB=BC,AC⊥BD交于点O.
(1)求证:四边形ABCD为菱形;
(2)如图2,过四边形ABCD的顶点A作AE⊥BC于点E,交OB于点H,若AB=AC=6,求四边形OHEC的面积.
15.如图所示,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,且AB=12,BC=16.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC于点E,求∠BDF的度数.
16.在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF中点.连接BE、CE、AE.
(1)求证:∠DAE=∠ADE;
(2)求证:△AEB≌△DEC;
(3)当EB=BC时,求∠AFD的度数.
17.如图①正方形ABCD中,点E是对角线AC上任意一点,连接DE,BE.
(1)求证:DE=BE;
(2)当AE=AB时,求∠BED的度数;
(3)如图②,过点E作EF⊥DE交AB于点F,当BE=BF时,若AB.求AF的长.
18.在菱形ABCD中,对角线AC、BD相交于点O,过点O直线EF分别交DA、BC的延长线于点E、F,连接BE、DF.
(1)求证:△AOE≌△COF;
(2)若EF=BD,BE=8,BF=16,求菱形ABCD的面积;
(3)若EF⊥AB,垂足为G,OB=3AG,求的值.
参考答案
一、选择题
1—8:CDDACBCD
二、填空题
9.【解答】解:∵四边形ABCD是菱形,
∴AB=AD,
当PM⊥AB,PN⊥AD时,
PM+PN的值最小,最小值=AD边上的高,设这个高为h,
AB PM+ AD PN=AD h,
∴PM+PN=h=AB sin60°=3,
故答案为:
10.【解答】解:∵BE=6,BF=EF,
∴BF=2,EF=4,故①正确;
如图1,当点E在AD上时,取BE的中点H,连接AH,
∵点H是BE的中点,∠BAE=90°,
∴AH=BH=HE=3,
∴AB=AH=BH=3,
∴△ABH是等边三角形,
∴∠ABE=60°,
∴∠EBC=30°,
∵BE=BC,
∴∠BCE=∠BEC=75°,
∴∠DCE=15°,故②正确;
如图2,当∠EBC=60°时,设AD与CE交于H,与BE交于点G,
∵∠EBC=60°,BC=BE,
∴△EBC是等边三角形,
∴∠EBC=∠ECB=60°=∠BEC,
∴∠ABG=∠DCE=30°,
∴AB=AG,CD=DH,
∴AG=DH=,
∴GH=6﹣2,
∵AD∥BC,
∴∠EGH=∠EBC=60°,∠GHE=∠BCE=60°,
∴△GEH是等边三角形,
∴EH=GH=6﹣2≠DH,
∴∠ADE≠∠DEH,
∴∠ADE≠30°;故③错误;
如图3,在BC上截取BM=BF=2,连接EM,DM,
∵BE=BC,∠EBM=∠CBF,
∴△BFC≌△BME(SAS),
∴CF=EM,
∴DE+CF=DE+EM,
∴当点E,点D,点M三点共线时,DE+CF有最小值,最小值为DM的长,
∵CM=BC﹣BM=4,CD=AB=3,
∴DM===5,
∴DE+CF的最小值为5,故④正确;
故答案为:①②④.
11.【解答】解:①∵E是BC边的中点,
∴BE=CE,
由折叠知,∠AEB=∠AEF,BE=EF,
∴CE=EF,
∴∠ECF=∠EFC,
∵∠BEF=∠ECF+∠EFC,
∴∠AEB=∠ECF,
∴AE∥CF,
故①正确;
②由折叠知AB=AF,∠ABE=∠AFE=90°,∠BAE=∠FAE,
∵正方形ABCD中,AB=AD,∠ADG=90°,
∴AD=AF,
∵AG=AG,
∴Rt△ADG≌Rt△AFG(HL),
∴∠DAG=∠FAG,DG=FG
∴∠BAE+∠DAG=∠EAF+∠FAG,BE+DG=EF+FG
∴∠EAG=,BE+DG=EG,
故②正确;
③设正方形ABCD的边长为a,CG=x,则EC=BE=EF=a,GF=DG=a﹣x,
在△CEG中,由勾股定理得,
,
解得,x=a,
∴,
∵EF:EG=a:(a+a﹣a)=3:5,
∴=,
故③错误;
④由上可知DG=a﹣x=a﹣a=a,
∵AD=a,
∴AD=3DG,
故④正确;
故答案为:①②④.
12.【解答】解:过点C作CE⊥x轴于点E,过点M作MF⊥x轴于点F,连接EM,
∴∠MFO=∠CEO=∠AOB=90°,AO∥MF∥CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,AM=CM,
∴∠OAB=∠EBC,OF=EF,
∴MF是梯形AOEC的中位线,
∴MF=(AO+EC),
∵MF⊥OE,
∴MO=ME.
∵在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴OB=CE,AO=BE.
∴MF=(BE+OB),
又∵OF=FE,
∴△MOE是直角三角形,
∵MO=ME,
∴△MOE是等腰直角三角形,
∴OE==6,
∵A(0,2),
∴OA=2,
∴BE=2,
∴OB=CE=4.
∴C(6,4).
故答案为:(6,4).
三、解答题
13.【解答】(1)证明:∵△ABC中,AB=AC,AD平分∠BAC,
∴AD⊥BC,∠ADB=90°,
∵BE∥AD,AE⊥AD,
∴∠DBE=90°,∠DAE=90°,
∴四边形ADBE是矩形;
(2)解:∵AB=AC,AD平分∠BAC,BC=4,AD=3,
∴.
在直角三角形ABD中,由勾股定理得:.
∵四边形ADBE是矩形,
∴BE=AD=3,AE=BD=2.
∵,
∴.
14.【解答】(1)证明:∵AD=AB,AC⊥BD,
∴AC垂直平分BD,
∴BC=CD,
∴BC=CD=AD=AB,
∴四边形ABCD为菱形;
(2)解:如图,连接CH,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC,
∵AB=AC=6,
∴AB=AC=BC=6,
∴△ABC是等边三角形,
∵AE⊥CB,6
∴BE=CE=3,
∴AE,
∵AO=OC,BE=EC,
∴S△AOH=S△OCH=S△ECH=S△BEH,
∴.
15.【解答】(1)证明:∵在四边形ABCD中,对角线AC,BD相交于点O,AO=CO=10,BO=DO,
∴四边形ABCD是平行四边形,AC=AO+CO=20,
∵AB=12,BC=16,
∴AB2+BC=122+162=202=AC2,
∴∠ABC=90°,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形
∴∠ADC=90°,
∵∠ADF:∠FDC=3:2,∠ADF+∠FDC=∠ADC,
∴,
∵DF⊥AC,
∴∠DCO=90°﹣36°=54°,
∵四边形ABCD是矩形,
∴CO=OD,
∴∠ODC=∠DCO=54°,
∴∠BDF=∠ODC﹣∠FDC=18°.
16.【解答】(1)证明:∵ABCD为正方形,
∴∠BAD=90°,
∵点E为DF中点,
∴AE=EF=DEDF,
∴∠EAD=∠EDA;
(2)证明:∵四边形ABCD是正方形,
∴AB=CD,∠BAD=∠ADC=90°,
∵∠EAD=∠EDA,
∵∠BAE=∠BAD﹣∠EAD,∠CDE=∠ADC﹣∠EDA,
∴∠BAE=∠CDE,
在△AEB和△DEC中,
,
∴△AEB≌△DEC(SAS);
(3)解:∵△AEB≌△DEC,
∴EB=EC,
∵EB=BC,
∴EB=BC=EC,
∴△BCE是等边三角形,
∴∠EBC=60°,
∴∠ABE=90°﹣60°=30°,
∵EB=BC=AB,
∴∠BAE(180°﹣30°)=75°,
又∵AE=EF,
∴∠AFD=∠BAE=75°.
17.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠DAE=∠BAE,
∵AE=AE,
∴△DAE≌△BAE(SAS),
∴DE=BE;
(2)∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
由(1)知:△DAE≌△BAE,
∴∠AED=∠AEB(180°﹣45°)135°,
∴∠BED=2∠AEB=135°;
(3)如图②,过E作EM⊥BF,
∵四边形ABCD是正方形,
∴CD=CB,∠DCE=∠BCE,
∵CE=CE,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵∠ADC=∠ABC=90°,
∴∠ADE=∠ABE,
∵DE⊥EF,
∴∠DEF=90°,
在四边形ADEF中,∠DAF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠BFE=180°,
∴∠BFE=∠EBF,
∴BE=EF,
∵BE=BF,
∴△BEF是等边三角形,
∴∠EBF=60°,
设BM=x,则MF=BM=x,EMx,
∵四边形ABCD是正方形,
∴∠BAE∠BAD=45°,
∴AM=EMx,
∵AM+BM=AB,
∴xx,
解得,x,
∴BF=2x=2,
∴AF=AB﹣BF2.
18.【解答】证明:(1)∵四边形ABCD是菱形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO,又∠AOE=∠COF
∴△AOE≌△COF(ASA);
(2)由△AOE≌△COF,得OE=OF,
∵四边形ABCD是菱形,∴OB=OD
∴四边形EBFD是平行四边形,
∵EF=BD,
∴ EBFE是矩形,∴∠EBF=90°,
设菱形ABCD的边长为x,∴AB=AD=x,∴AE=16﹣x,
在Rt△AEB中,根据勾股定理,得
AB2=AE2+BE2,即x2=(16﹣x)2+82,解得x=10,
∴S菱形=BC BE=10×8=80.
答:菱形ABCD的面积为80.
(3)∵EF⊥AB,垂足为G,
∵四边形ABCD是菱形,
∴OA⊥OB,
∵OG⊥AB,
设AG=a,则OB=3AG=3a,
设OA=x,AB=AD=y,
∵S△AOBAO OBAB OG,
∴3ax=y OG,
∴OG,
在Rt△GOA中,根据勾股定理,得
OG2=OA2﹣AG2,
∴()2=x2﹣a2,
整理,得(y2﹣90a2)x2=a2y2,
∴x2,
在Rt△BOA中,根据勾股定理,得
AB2=OB2+OA2,
∴y2=90a2+x2,
∴x2,
∴x4﹣a2x2﹣90a4=0,
解得x2=10a2或x2=﹣9a2(舍去),
∴xa,
y=10a,
∴OAAG,
∴
答:的值为.
21世纪教育网(www.21cnjy.com)
