第九章中心对称图形—平行四边形单元A卷(含答案)
文档属性
| 名称 | 第九章中心对称图形—平行四边形单元A卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 451.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-05 17:29:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章中心对称图形—平行四边形单元A卷苏科版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.正六边形最少旋转n度后能与自身重合,则n为( )
A.30 B.45
C.60 D.90
2.如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE2+DC2=DE2.
其中正确的个数是( )
A.1 B.2
C.3 D.4
3.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
7.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
8.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题5分,满分20分)
9.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,且AB=2,∠AOB=60°,点E为BD上一点,OE=1.连接AE,则AE的长为 .
12.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
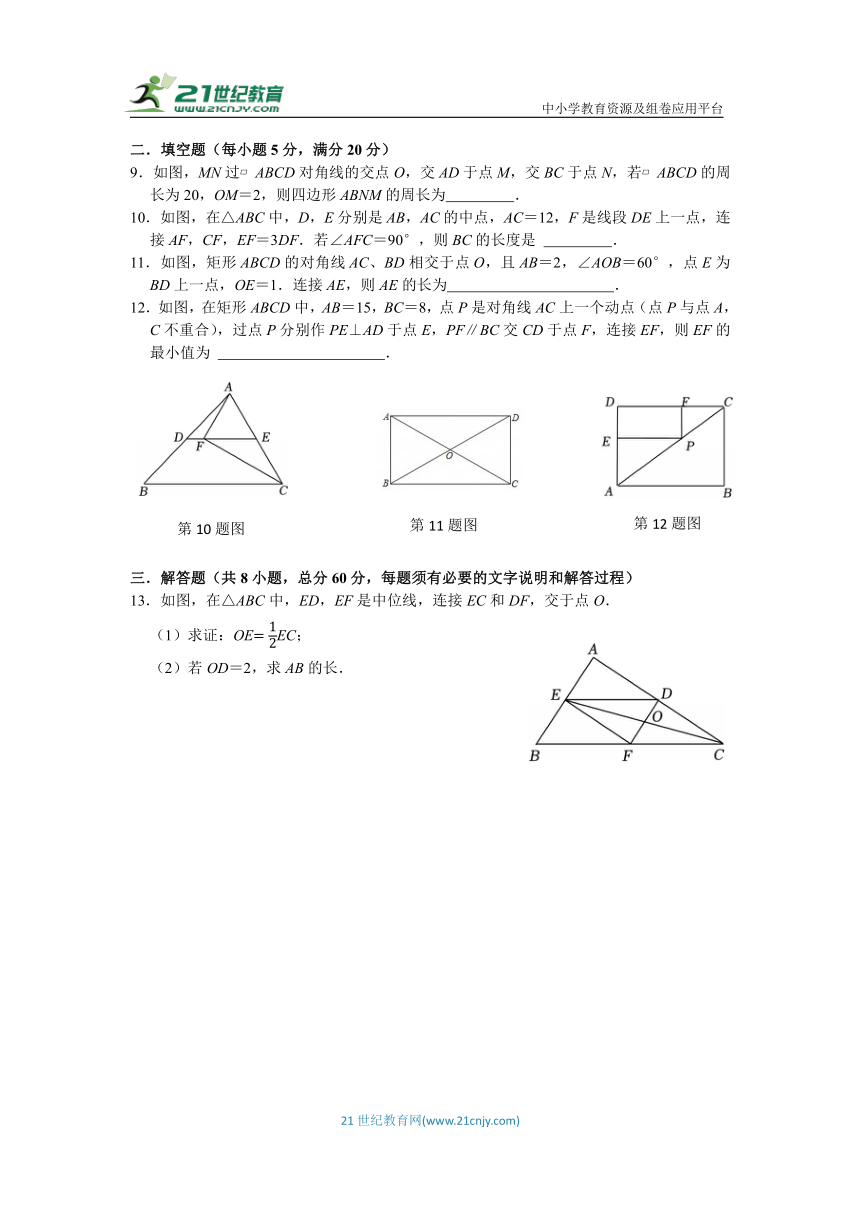
13.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OEEC;
(2)若OD=2,求AB的长.
14.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
15.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
16.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=3,OE=2,BF=5,求DF的长.
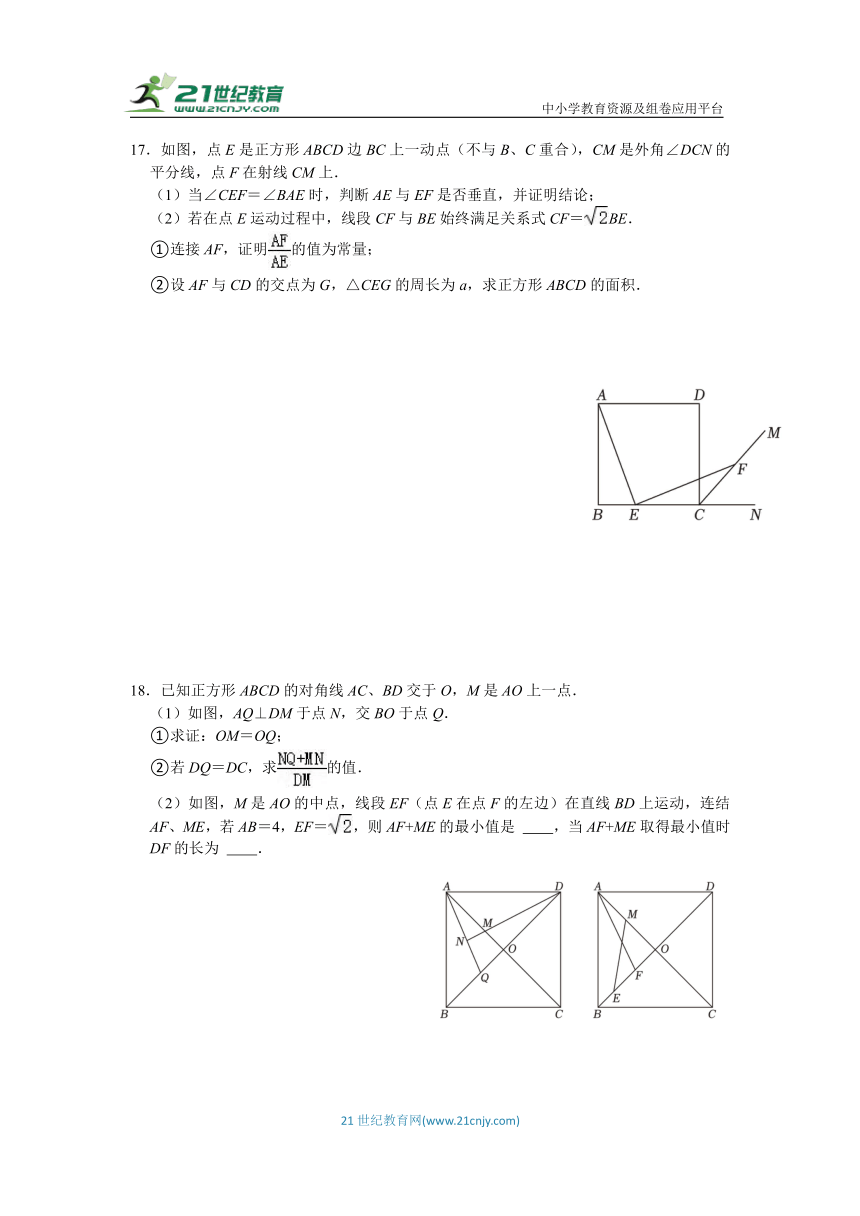
17.如图,点E是正方形ABCD边BC上一动点(不与B、C重合),CM是外角∠DCN的平分线,点F在射线CM上.
(1)当∠CEF=∠BAE时,判断AE与EF是否垂直,并证明结论;
(2)若在点E运动过程中,线段CF与BE始终满足关系式CF=BE.
①连接AF,证明的值为常量;
②设AF与CD的交点为G,△CEG的周长为a,求正方形ABCD的面积.
18.已知正方形ABCD的对角线AC、BD交于O,M是AO上一点.
(1)如图,AQ⊥DM于点N,交BO于点Q.
①求证:OM=OQ;
②若DQ=DC,求的值.
(2)如图,M是AO的中点,线段EF(点E在点F的左边)在直线BD上运动,连结AF、ME,若AB=4,EF=,则AF+ME的最小值是 ,当AF+ME取得最小值时DF的长为 .
参考答案
一、选择题
1—8:CCBBBBDB
二、填空题
9.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
10.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
11.【解答】解:当点E在OB上或在OD上时,如图,
∵四边形ABCD是矩形,
∴OA=OBAC,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,
①当点E在OB上时,OE=1,
∴BE=1,
∴E是OB的中点,
∴AE⊥OB,
∴OA=2,
∴AE;
②当点E在OD上时为E′,
∴EE′=2,
∴AE′.
则AE的长为:或.
故答案为:或.
12.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
13.【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF,
∴AB=2DF=8.
14.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
15.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
16.【解答】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:由(1)知,四边形AEFD为矩形,
∴DF=AE,AF=DE=2OE=4,
∵AB=3,DE=4,BF=5,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴S△ABF,
∴AB×AF=BF×AE,
即3×4=5AE,
∴AE,
∴DF=AE.
17.【解答】(1)解:垂直,理由如下:
∵四边形ABCD是正方形,
∴∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠CEF=∠BAE,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴AE⊥EF;
(2)①证明:如图1,
作FG⊥BN于G,
∵四边形ABCD是正方形,
∴∠DCN=∠BCD=90°,AB=BC,
∵CMP平分∠DCN,
∴∠DCM=∠MCN=45°,
∴CF=,
∵CF=,
∴BE=CG=CF,
∴BE+EC=CG+EC,
∴BC=EG,
∴EG=AB,
∵∠FCG=∠B=90°,
∴△ABE≌△EGF(SAS),
∴AE=EF,∠FEG=∠BAE,
∴由(1)得:∠AEF=90°,
∴=;
②解:如图2,
在CB的延长线上截取BH=DG,连接AH,
∵四边形ABCD是正方形,
∴∠ABH=∠ABC=∠BAD=∠D=90°,AB=AD=BC=CD,
∴△ABH≌△ADG(SAS),
∴∠DAG=∠BAH,AH=AG,
由①知:∠EAF=45°,
∴∠BAE+∠DAG=45°,
∴∠BAE+∠BAH=45°,
∴∠EAH=45°,
∴∠EAH=∠EAF,
∵AE=AE,
∴△AEH≌△AEG,
∴EG=EH=BH+BE=DG+BE,
∴EG+CG+EC=DG+BE+CG+EC=CD+BC=2BC=a,
∴BC=,
∴S正方形ABCD=BC2=.
18.【解答】(1)①证明:∵在正方形ABCD中,AC=BD,AC⊥BD,OA=AC,OD=BD,
∴OA=OD,
∵AQ⊥DM,
∴∠DNQ=∠AOQ=90°,
∴∠QAO=∠ODM,
∴△AOQ≌△DOM(ASA),
∴OQ=OM;
②证明:连接ON,作OP⊥ON于O交MD于点P,
∴∠NOP=∠QOM=90°,
∴∠NOP﹣∠NOM=∠QOM﹣∠NOM,
即∠NOQ=∠POM,
由(1)得△AOQ≌△DOM,
∴OQ=OM,∠NQO=∠PMO,AQ=MD,
∴△NOQ≌△POM(ASA),
∴ON=OP,QN=MP,
∴QN+NM=MP+NM=NP,
又NP=ON,
∴QN+NM=ON,
∵DQ=DA,AQ⊥DM,
∴AN=NQ,
∵∠AOQ=90°,
∴AQ=2ON,
∴NQ+NM=AQ=MD,
∴=;
(3)解:∵正方形ABCD中,AB=4,
∴BD=4,
∴OD=2,
取AD的中点P,连接FP,MP,CP,且CP交BD于点H,
∵M为AO的中点,
∴MP∥OD,MP=OD=,
∵EF=,
∴EF=MP,
∴四边形MEFP为平行四边形,
∴ME=PF,
∵四边形ABCD是正方形,
∴A,C关于BD对称,
∴AF=CF,
∵AF+ME=CF+FP≥CP,
即F与H重合时,AF+ME最小,最小值为PC的长,
∵PD=2,CD=4,
∴PC===2,
∴AF+ME的最小值为2,
∴DF=BF=BD==.
故答案为:2,.
21世纪教育网(www.21cnjy.com)
第九章中心对称图形—平行四边形单元A卷苏科版2024—2025学年八年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.正六边形最少旋转n度后能与自身重合,则n为( )
A.30 B.45
C.60 D.90
2.如图,在Rt△ABC中,AB=AC,D,E是斜边上BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①BF⊥BC;②△AED≌△AEF;③BE+DC=DE;④BE2+DC2=DE2.
其中正确的个数是( )
A.1 B.2
C.3 D.4
3.下列关于平行四边形的说法中错误的是( )
A.平行四边形的对角相等,邻角互补
B.一组对边相等,一组对角相等的四边形是平行四边形
C.一组对边平行,一组对角相等的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
4.如图,要使平行四边形ABCD成为矩形,需要添加的条件是( )
A.∠ABD=∠CBD B.∠ABC=90° C.AC⊥BD D.AB=BC
5.菱形ABCD中,若对角线AC=8cm,BD=6cm,则菱形ABCD的周长是( )
A.25 B.20 C.15 D.10
6.如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.AD∥BC,OB=OD D.∠ABD=∠BDC,∠ADB=∠CBD
7.如图,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若AE=4,AF=6,且 ABCD的周长为40,则 ABCD的面积为( )
A.24 B.36 C.40 D.48
8.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②△DBF≌△ABC;③四边形AEFD是平行四边形;
④∠DFE=110°;⑤S四边形AEFD=5.正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二.填空题(每小题5分,满分20分)
9.如图,MN过 ABCD对角线的交点O,交AD于点M,交BC于点N,若 ABCD的周长为20,OM=2,则四边形ABNM的周长为 .
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是线段DE上一点,连接AF,CF,EF=3DF.若∠AFC=90°,则BC的长度是 .
11.如图,矩形ABCD的对角线AC、BD相交于点O,且AB=2,∠AOB=60°,点E为BD上一点,OE=1.连接AE,则AE的长为 .
12.如图,在矩形ABCD中,AB=15,BC=8,点P是对角线AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥AD于点E,PF∥BC交CD于点F,连接EF,则EF的最小值为 .
三.解答题(共8小题,总分60分,每题须有必要的文字说明和解答过程)
13.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OEEC;
(2)若OD=2,求AB的长.
14.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠CAB,CE⊥AE于点E,延长CE交AB于点D.
(1)求证:CE=DE;
(2)若点F为BC的中点,求EF的长.
15.如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,连接CD,过点C作CE∥AB,过点A作AE∥CD,CE,AE交于点E,连接DE交AC于点O.
(1)求证:四边形AECD是菱形;
(2)连接BE交AC于点F,交CD于点G,若DE=CE,CD=2,求OF的长.
16.如图,在 ABCD中,AE⊥BC于点E,延长BC至点F,使CF=BE,连接DF,AF与DE交于点O.
(1)求证:四边形AEFD为矩形;
(2)若AB=3,OE=2,BF=5,求DF的长.
17.如图,点E是正方形ABCD边BC上一动点(不与B、C重合),CM是外角∠DCN的平分线,点F在射线CM上.
(1)当∠CEF=∠BAE时,判断AE与EF是否垂直,并证明结论;
(2)若在点E运动过程中,线段CF与BE始终满足关系式CF=BE.
①连接AF,证明的值为常量;
②设AF与CD的交点为G,△CEG的周长为a,求正方形ABCD的面积.
18.已知正方形ABCD的对角线AC、BD交于O,M是AO上一点.
(1)如图,AQ⊥DM于点N,交BO于点Q.
①求证:OM=OQ;
②若DQ=DC,求的值.
(2)如图,M是AO的中点,线段EF(点E在点F的左边)在直线BD上运动,连结AF、ME,若AB=4,EF=,则AF+ME的最小值是 ,当AF+ME取得最小值时DF的长为 .
参考答案
一、选择题
1—8:CCBBBBDB
二、填空题
9.【解答】解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAM=∠OCN,
在△AMO和△CNO中,
,
∴△AMO≌△CNO(ASA),
∴OM=ON=2,AM=CN,
则四边形ABNM的周长=BN+AB+AM+MN=(BN+AM)+AB+MN=BC+AB+MN=10+4=14.
故答案为:14.
10.【解答】解:∵∠AFC=90°,
∴△AFC是直角三角形,
∵点E为AC的中点,AC=12,
∴,
∵F是线段DE上一点,连接AF,CF,EF=3DF,
∴,
∴DE=DF+EF=8,
∵D,E分别是AB,AC的中点,
∴DE是△ABC中位线,
∴BC=2DE=16,
故答案为:16.
11.【解答】解:当点E在OB上或在OD上时,如图,
∵四边形ABCD是矩形,
∴OA=OBAC,
∵∠AOB=60°,
∴△AOB是等边三角形,
∵AB=2,
①当点E在OB上时,OE=1,
∴BE=1,
∴E是OB的中点,
∴AE⊥OB,
∴OA=2,
∴AE;
②当点E在OD上时为E′,
∴EE′=2,
∴AE′.
则AE的长为:或.
故答案为:或.
12.【解答】解:如图,过点D作DP′⊥AC于P′,连接EF,DP,
∵四边形ABCD是矩形,AB=15,BC=8,
∴CD=AB=15,AD=BC=8,∠ADC=90°,
∴,
∵PF∥BC,
∴∠PFD+∠ADC=180°,
∴∠PFD=90°,
∵PE⊥AD,
∴∠PED=∠EDF=∠PFD=90°,
∴四边形DEPF是矩形,
∴EF=DP,
要使EF最小,只需DP最小,当DP⊥AC时,DP最小,最小值为DP′的长,
∵,
∴,
故EF的最小值为,
故答案为:.
三、解答题
13.【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF,
∴AB=2DF=8.
14.【解答】(1)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵CE⊥AE,
∴∠AEC=∠AED=90°,
在△AEC和△AED中,
,
∴△AEC≌△AED(ASA),
∴CE=DE;
(2)在Rt△ABC中,∵AC=6,BC=8,
∴,
∵△AEC≌△AED,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵点E为CD中点,点F为BC中点,
∴.
15.【解答】(1)证明:∵∠ACB=90°,点D是AB中点,
∴,
∵AE∥CD,CE∥AB,
∴四边形AECD是平行四边形,
∵CD=AD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AC⊥DE,CD=CE,OD=OE,
∵DE=CE,CD=2,
∴DE=CE=CD=2,△CDE为等边三角形,
∴∠AOD=∠ACB=90°,OD=OE=1,∠DEC=60°,
∴BC∥DE,
∵CE∥BD,
∴四边形BCED是平行四边形,
∵DE=CE,
∴四边形BCED是菱形,
∴,
∴EF=2OF,
由勾股定理得OF2=EF2﹣OE2,即OF2=(2OF)2﹣12,
解得.
16.【解答】(1)证明:∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AD=BC=EF,
又∵AD∥EF,
∴四边形AEFD为平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD为矩形;
(2)解:由(1)知,四边形AEFD为矩形,
∴DF=AE,AF=DE=2OE=4,
∵AB=3,DE=4,BF=5,
∴AB2+AF2=BF2,
∴△BAF为直角三角形,∠BAF=90°,
∴S△ABF,
∴AB×AF=BF×AE,
即3×4=5AE,
∴AE,
∴DF=AE.
17.【解答】(1)解:垂直,理由如下:
∵四边形ABCD是正方形,
∴∠B=90°,
∴∠BAE+∠AEB=90°,
∵∠CEF=∠BAE,
∴∠CEF+∠AEB=90°,
∴∠AEF=90°,
∴AE⊥EF;
(2)①证明:如图1,
作FG⊥BN于G,
∵四边形ABCD是正方形,
∴∠DCN=∠BCD=90°,AB=BC,
∵CMP平分∠DCN,
∴∠DCM=∠MCN=45°,
∴CF=,
∵CF=,
∴BE=CG=CF,
∴BE+EC=CG+EC,
∴BC=EG,
∴EG=AB,
∵∠FCG=∠B=90°,
∴△ABE≌△EGF(SAS),
∴AE=EF,∠FEG=∠BAE,
∴由(1)得:∠AEF=90°,
∴=;
②解:如图2,
在CB的延长线上截取BH=DG,连接AH,
∵四边形ABCD是正方形,
∴∠ABH=∠ABC=∠BAD=∠D=90°,AB=AD=BC=CD,
∴△ABH≌△ADG(SAS),
∴∠DAG=∠BAH,AH=AG,
由①知:∠EAF=45°,
∴∠BAE+∠DAG=45°,
∴∠BAE+∠BAH=45°,
∴∠EAH=45°,
∴∠EAH=∠EAF,
∵AE=AE,
∴△AEH≌△AEG,
∴EG=EH=BH+BE=DG+BE,
∴EG+CG+EC=DG+BE+CG+EC=CD+BC=2BC=a,
∴BC=,
∴S正方形ABCD=BC2=.
18.【解答】(1)①证明:∵在正方形ABCD中,AC=BD,AC⊥BD,OA=AC,OD=BD,
∴OA=OD,
∵AQ⊥DM,
∴∠DNQ=∠AOQ=90°,
∴∠QAO=∠ODM,
∴△AOQ≌△DOM(ASA),
∴OQ=OM;
②证明:连接ON,作OP⊥ON于O交MD于点P,
∴∠NOP=∠QOM=90°,
∴∠NOP﹣∠NOM=∠QOM﹣∠NOM,
即∠NOQ=∠POM,
由(1)得△AOQ≌△DOM,
∴OQ=OM,∠NQO=∠PMO,AQ=MD,
∴△NOQ≌△POM(ASA),
∴ON=OP,QN=MP,
∴QN+NM=MP+NM=NP,
又NP=ON,
∴QN+NM=ON,
∵DQ=DA,AQ⊥DM,
∴AN=NQ,
∵∠AOQ=90°,
∴AQ=2ON,
∴NQ+NM=AQ=MD,
∴=;
(3)解:∵正方形ABCD中,AB=4,
∴BD=4,
∴OD=2,
取AD的中点P,连接FP,MP,CP,且CP交BD于点H,
∵M为AO的中点,
∴MP∥OD,MP=OD=,
∵EF=,
∴EF=MP,
∴四边形MEFP为平行四边形,
∴ME=PF,
∵四边形ABCD是正方形,
∴A,C关于BD对称,
∴AF=CF,
∵AF+ME=CF+FP≥CP,
即F与H重合时,AF+ME最小,最小值为PC的长,
∵PD=2,CD=4,
∴PC===2,
∴AF+ME的最小值为2,
∴DF=BF=BD==.
故答案为:2,.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
